2ND QUARTER 2007, VOLUME 9, NO. 2
www.comsoc.org/pubs/surveys
CHANNEL ESTIMATION FOR
WIRELESS OFDM SYSTEMS
MEHMET KEMAL OZDEMIR, LOGUS BROADBAND WIRELESS SOLUTIONS, INC. AND
HUSEYIN ARSLAN, UNIVERSITY OF SOUTH FLORIDA
ABSTRACT
Orthogonal frequency division multiplexing (OFDM) is a special case of
multi-carrier transmission and it can accommodate high data rate require-
ment of multimedia based wireless systems. Since channel estimation is an
integral part of OFDM systems, it is critical to understand the basis of
channel estimation techniques for OFDM systems so that the most appro-
priate method can be applied. In this article, an extensive overview of chan-
nel estimation techniques employed in OFDM systems are presented. In
addition, the advantages, drawbacks, and relationship of these estimation
techniques with each other are analyzed and discussed. As the combination
of multiple input multiple output (MIMO)-OFDM systems promises higher
data rates, estimation techniques are further investigated for these systems.
Although the existing proposed techniques differ in terms of computational
complexity and their mean squared error (MSE) performance, it has been
observed that many channel estimation techniques are indeed a subset of
LMMSE channel estimation technique. Hence, based on a given system’s
resources and specifications, a suitable method among the presented tech-
niques can be applied.
D
riven by multimedia based applications, anticipated
future wireless systems will require high data rate
capable technologies. Novel techniques such as
OFDM and MIMO stand as promising choices for future high
data rate systems [1, 2].
OFDM divides the available spectrum into a number of
overlapping but orthogonal narrowband subchannels, and
hence converts a frequency selective channel into a non-
frequency selective channel [3]. Moreover, ISI is avoided by
the use of CP, which is achieved by extending an OFDM
symbol with some portion of its head or tail [4]. With these
vital advantages, OFDM has been adopted by many wire-
less standards such as DAB, DVB, WLAN, and WMAN [5,
6].
MIMO, on the other hand, employs multiple antennas at
the transmitter and receiver sides to open up additional sub-
channels in spatial domain. Since parallel channels are estab-
lished over the same time and frequency, high data rates
without the need of extra bandwidth are achieved [7, 8]. Due
to this bandwidth efficiency, MIMO is included in the stan-
dards of future BWA [9]. Overall, these benefits have made
the combination of MIMO-OFDM an attractive technique for
future high data rate systems [10–12].
As in many other coherent digital wireless receivers, chan-
nel estimation is also an integral part of the receiver designs
in coherent MIMO-OFDM systems [13]. In wireless systems,
transmitted information reaches to receivers after passing
through a radio channel. For conventional coherent receivers,
the effect of the channel on the transmitted signal must be
estimated to recover the transmitted information [14]. As long
as the receiver accurately estimates how the channel modifies
the transmitted signal, it can recover the transmitted informa-
tion. Channel estimation can be avoided by using differential
modulation techniques, however, such systems result in low
data rate and there is a penalty for 3–4 dB SNR [15 19]. In
some cases, channel estimation at user side can be avoided if
the base station performs the channel estimation and sends a
pre-distorted signal [20]. However, for fast varying channels,
the pre-distorted signal might not bear the current channel
distortion, causing system degradation. Hence, systems with a
channel estimation block are needed for the future high data
rate systems.
Channel estimation is a challenging problem in wireless
systems. Unlike other guided media, the radio channel is high-
ly dynamic. The transmitted signal travels to the receiver by
undergoing many detrimental effects that corrupt the signal
18
1553-877X
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
�
CIR
CFR
s
t
n
e
i
c
i
f
f
e
o
C
DFT/IDFT
s
t
n
e
i
c
i
f
f
e
o
C
Tap index
Subcarrier index
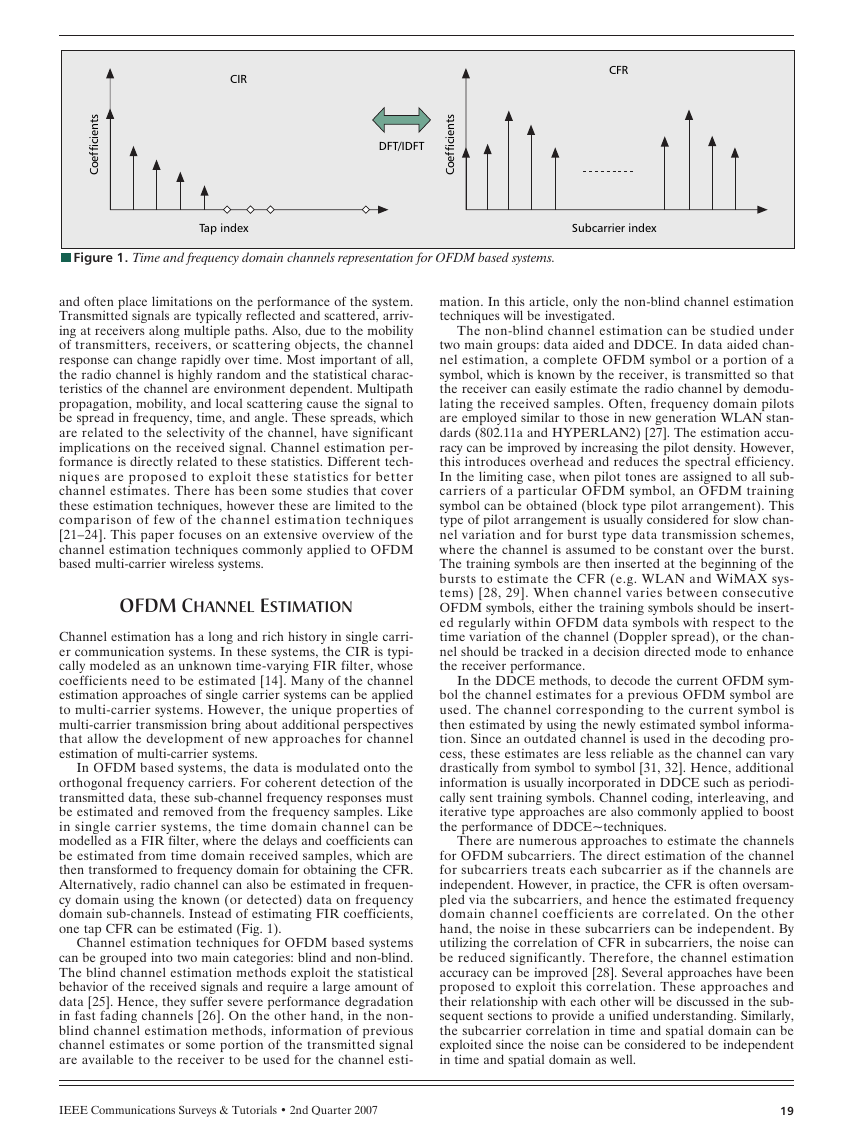
nFigure 1. Time and frequency domain channels representation for OFDM based systems.
and often place limitations on the performance of the system.
Transmitted signals are typically reflected and scattered, arriv-
ing at receivers along multiple paths. Also, due to the mobility
of transmitters, receivers, or scattering objects, the channel
response can change rapidly over time. Most important of all,
the radio channel is highly random and the statistical charac-
teristics of the channel are environment dependent. Multipath
propagation, mobility, and local scattering cause the signal to
be spread in frequency, time, and angle. These spreads, which
are related to the selectivity of the channel, have significant
implications on the received signal. Channel estimation per-
formance is directly related to these statistics. Different tech-
niques are proposed to exploit these statistics for better
channel estimates. There has been some studies that cover
these estimation techniques, however these are limited to the
comparison of few of the channel estimation techniques
[21–24]. This paper focuses on an extensive overview of the
channel estimation techniques commonly applied to OFDM
based multi-carrier wireless systems.
OFDM CHANNEL ESTIMATION
Channel estimation has a long and rich history in single carri-
er communication systems. In these systems, the CIR is typi-
cally modeled as an unknown time-varying FIR filter, whose
coefficients need to be estimated [14]. Many of the channel
estimation approaches of single carrier systems can be applied
to multi-carrier systems. However, the unique properties of
multi-carrier transmission bring about additional perspectives
that allow the development of new approaches for channel
estimation of multi-carrier systems.
In OFDM based systems, the data is modulated onto the
orthogonal frequency carriers. For coherent detection of the
transmitted data, these sub-channel frequency responses must
be estimated and removed from the frequency samples. Like
in single carrier systems, the time domain channel can be
modelled as a FIR filter, where the delays and coefficients can
be estimated from time domain received samples, which are
then transformed to frequency domain for obtaining the CFR.
Alternatively, radio channel can also be estimated in frequen-
cy domain using the known (or detected) data on frequency
domain sub-channels. Instead of estimating FIR coefficients,
one tap CFR can be estimated (Fig. 1).
Channel estimation techniques for OFDM based systems
can be grouped into two main categories: blind and non-blind.
The blind channel estimation methods exploit the statistical
behavior of the received signals and require a large amount of
data [25]. Hence, they suffer severe performance degradation
in fast fading channels [26]. On the other hand, in the non-
blind channel estimation methods, information of previous
channel estimates or some portion of the transmitted signal
are available to the receiver to be used for the channel esti-
mation. In this article, only the non-blind channel estimation
techniques will be investigated.
The non-blind channel estimation can be studied under
two main groups: data aided and DDCE. In data aided chan-
nel estimation, a complete OFDM symbol or a portion of a
symbol, which is known by the receiver, is transmitted so that
the receiver can easily estimate the radio channel by demodu-
lating the received samples. Often, frequency domain pilots
are employed similar to those in new generation WLAN stan-
dards (802.11a and HYPERLAN2) [27]. The estimation accu-
racy can be improved by increasing the pilot density. However,
this introduces overhead and reduces the spectral efficiency.
In the limiting case, when pilot tones are assigned to all sub-
carriers of a particular OFDM symbol, an OFDM training
symbol can be obtained (block type pilot arrangement). This
type of pilot arrangement is usually considered for slow chan-
nel variation and for burst type data transmission schemes,
where the channel is assumed to be constant over the burst.
The training symbols are then inserted at the beginning of the
bursts to estimate the CFR (e.g. WLAN and WiMAX sys-
tems) [28, 29]. When channel varies between consecutive
OFDM symbols, either the training symbols should be insert-
ed regularly within OFDM data symbols with respect to the
time variation of the channel (Doppler spread), or the chan-
nel should be tracked in a decision directed mode to enhance
the receiver performance.
In the DDCE methods, to decode the current OFDM sym-
bol the channel estimates for a previous OFDM symbol are
used. The channel corresponding to the current symbol is
then estimated by using the newly estimated symbol informa-
tion. Since an outdated channel is used in the decoding pro-
cess, these estimates are less reliable as the channel can vary
drastically from symbol to symbol [31, 32]. Hence, additional
information is usually incorporated in DDCE such as periodi-
cally sent training symbols. Channel coding, interleaving, and
iterative type approaches are also commonly applied to boost
the performance of DDCE~techniques.
There are numerous approaches to estimate the channels
for OFDM subcarriers. The direct estimation of the channel
for subcarriers treats each subcarrier as if the channels are
independent. However, in practice, the CFR is often oversam-
pled via the subcarriers, and hence the estimated frequency
domain channel coefficients are correlated. On the other
hand, the noise in these subcarriers can be independent. By
utilizing the correlation of CFR in subcarriers, the noise can
be reduced significantly. Therefore, the channel estimation
accuracy can be improved [28]. Several approaches have been
proposed to exploit this correlation. These approaches and
their relationship with each other will be discussed in the sub-
sequent sections to provide a unified understanding. Similarly,
the subcarrier correlation in time and spatial domain can be
exploited since the noise can be considered to be independent
in time and spatial domain as well.
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
19
�
Data
bits
Coding,
modulation,
interleaving
Cyclic
prefix
IFFT
K-
point
Cyclic
prefix
IFFT
K-
point
X1
K
K
XNtx
S
/
P
S
/
P
P
/
S
P
/
S
Ant #1
Ant #1
Wireless
channel
Ant #Ntx
Ant #Nrx
S
/
P
S
/
P
Remove
Cyclic prefix
IFFT
K-
point
Remove
Cyclic prefix
IFFT
K-
point
P
/
S
P
/
S
Y1
K
K
YNrx
Deinterleaving,
demodulation,
decoding
Output
bits
CSI
nFigure 2. MIMO-OFDM transceiver model.
Although it is a common approach to assume the channel
to be constant over an OFDM symbol duration [9, 27], for
fast fading channels the same assumption leads to ICI [33],
which degrades the channel estimation performance. Hence,
the methods employed in data-aided and decision directed
channel estimation need to be modified so that the variation
of the channel over the OFDM symbol is taken into account
for better estimates. External interfering sources also affect
the performance of channel estimation. The effect of interfer-
ing sources can be mitigated by exploiting their statistical
properties. Although most systems treat ICI and external
interference as part of noise, better channel estimation perfor-
mance can be obtained by more accurate modeling [34].
There are basically three basic blocks affecting the perfor-
mance of the non-blind channel estimation techniques. These
are the pilot patterns, the estimation method, and the signal
detection part. Each method covered in this article either
tackles one of the above basic block or several at a time. The
specific choice depends on the wireless system specifications
and the channel condition. The aspects of each method are
presented such that a suitable method can easily be selected
for a given wireless system and channel conditions. It can be
observed that each method can be approximated to the other
methods by using the same set of variables. For example, in
this paper it is shown that each estimation method is indeed a
subset of LMMSE technique.
In the literature, initial channel estimation methods have
been mostly developed for SISO-OFDM systems, that is, sin-
gle antenna systems. With the emergence of MIMO-OFDM,
these methods need some modifications as the received signal
in MIMO-OFDM is the superposition of all the transmitted
signals of a given user. In many cases, the methods of SISO-
OFDM are easily adopted for MIMO-OFDM but novel meth-
ods exploiting space-time codes or other MIMO specific
elements are also introduced.
In the rest of the article, starting from a generic system
model, the channel estimation techniques will be presented
starting from the less complicated techniques. More emphasis
will be given on data aided channel estimation as it provides
some unique approaches for OFDM systems. Discussions on
ICI, external interferers, and MIMO systems as well as related
issues will also be given. Finally, some concluding remarks and
potential research areas will be given at the end of the article.
NOTATION
Matrices and the vectors are denoted with boldface letters,
where the upper/lower letters will be used for frequency/time
domain variables; (.)H denotes conjugate-transpose; E{.}
denotes expected value; diag(x) stands for diagonal matrix
with the column vector x on its diagonal; 0a×b denotes a
matrix of a × b with zero entries; IN denotes N × N identity
matrix; and j=√
——
–1.
SYSTEM MODEL
A generic block diagram of a basic baseband-equivalent
MIMO-OFDM system is given in Fig. 2. A MIMO-OFDM
system with Ntx transmit and Nrx receive antennas is assumed.
The information bits can be coded and interleaved. The coded
bits are then mapped into data symbols depending on the
modulation type. Another stage of interleaving and coding
can be performed for the modulated symbols. Although the
symbols are in time domain, the data up to this point is con-
sidered to be in the frequency domain. The data is then de-
multiplexed for different transmitter antennas. The serial data
symbols are then converted to parallel blocks, and an IFFT is
applied to these parallel blocks to obtain the time domain
OFDM symbols. For the transmit antenna, tx, time domain
samples of an OFDM symbol can be obtained from frequency
domain symbols as
x n m IFFT X n k
(1)
tx
[ , ]}
[ ,
=
{
]
tx
=
K
1
−
∑
k
=
0
[ ,
X n
tx
]
kk e
2
j mk K
π
/
(1)
0
≤
,
k m K
≤
−
1
(2)
where Xtx[n, k] is the data at the kth subcarrier of the nth
OFDM symbol, K is the number of subcarriers, and m is the
time domain sampling index. After the addition of CP, which
is larger than the expected maximum excess delay of the chan-
nel, and D/A conversion, the signals from different transmit
antennas are sent through the radio channel.
The channel between each transmitter/receiver link is mod-
elled as a multi-tap channel with the same statistics [3]. The
typical channel at time t is expressed as,
( , )
h t
τ
=
L
1
−
α δ τ τ
l
( ) (
tl
−
∑
l
=
0
),
(3)
where L is the number of taps, αl is the lth complex path gain,
and τl is the corresponding path delay. The path gains are
WSS complex Gaussian processes. The individual paths can be
20
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
�
correlated, and the channel can be sparse.
At time t, the CFR of the CIR is given by,
variables in matrix notation, for rxth receive antenna and nth
OFDM symbol, we get
( ,
H t
f
)
=
+∞∫
−∞
( , )
h t
e
τ
−
j
f
τπ τ2
.
d
(4)
Y
rx
=
tx
N
∑ Ξ
F
1
tx
=
H
F X
rxtx
+
I W
rx
rx
+
,
tx
With proper CP and timing, the CFR can be written as [3],
H n k H nT k f
[ , ]
(
,
≡
f
L
1
−
∑∆
=
)
l
=
0
kl
[ , ]
h n l F
K
,
(5)
where h[n, l] = h(nTf, kts), FK = e–j2π/K, Tf is the symbol
length including CP, ∆f is the subcarrier spacing, and ts = 1/Df
is the sample interval. In matrix notations, for the nth OFDM
symbol, Eq. 5 can be rewritten as
H = Fh
(6)
where H is the column vector containing the channel at each
subcarrier, F is the unitary FFT matrix, and h is the column
vector containing the CIR taps.
At the receiver, the signal from different transmit anten-
nas are received along with noise and interference. After per-
fect synchronization, down sampling, and the removal of the
CP, the simplified received baseband model of the samples
for a given receive antenna, rx, can be formulated as
y n m
rx
[ ,
]
=
+
Nt
xx
L
1
−
−
[ ,
]
x n m l h
tx
∑
∑
1
0
l
tx
=
=
[ ,
i n m w n m
rx
[ ,
+
]
rx
],
m
rxtx
[ , ]
n l
(7)
where rx =1, …, Nrx, the time domain effective CIR, h m
rxtx[n, l],
over an OFDM symbol is given as time-variant linear filter
depending on the time selectivity of the channel. Please note
that n represents OFDM symbol number, while m denotes the
sampling index in time domain so that h m
rxtx[n, l] is the CIR at
the sampling time index m for the symbol n. When the CIR is
constant over an OFDM symbol duration, then h m
rxtx[n, l] will
be the same for all m values, and hence the superscript m can
be dropped. Moreover, irx[n, m] is the term representing
external interference, wrx[n, m] is the AWGN sample with
2. After taking FFT of the time
zero mean and variance of σw
domain samples of Eq. 7, the received samples in frequency
domain can be expressed as,
[ , ]
Y n k
rx
=
=
+
−
j
2
km
π
K
]
y n m e
rx
K
1
−
0
=
m
[ ,
∑1
K
∑∑1
∑
K
Ntx
1
−
1
−
K
L
⎡⎡
⎢
⎣
m
=
0
tx
1
=
l
=
0
(8)
[ , ]
n l
]
x n m l h
tx
[ ,
−
m
rxtx
] −
]
i n m w n m e
rx
[ ,
[ ,
+
]
rx
j
2π
km
K
]
x n k e
′
tx
[ ,
j
2
(π
m l
−
))
/′
k K
(9)
(10)
⎤
⎥
⎦
=
(
Ntx
K
1
−
L
1
−
∑∑∑
tx
1
=
m
=
0
l
=
0
1
K
⎡
⎢
⎣
K
1
−
∑
⎡
⎢
⎣
2π
km
K
′=
0
k
−
j
m
rxtx
⎤⎦
[ , ]
n l e
h
where Irx[n, k] and Wrx[n, k] are the corresponding frequency
domain components calculated from irx[n, m]’s and wrx[n, m]’s,
respectively. After arranging the terms, and representing the
[
I n k W n
rx
[ , ]
,, ]k
+
+
rx
(11)
(12)
=
Ntx
∑ ΨX
1
tx
=
+
I W
rx
rx
+
.
tx
Here, Yrx is column vector storing the received signal at each
subcarrier, F is the unitary FFT matrix with entries
—
e–j2πmk/K√
K with m and k being the row and column index and
Ψ = FΞrxtxFH, which can be considered as the equivalent
channel between each received and all the transmitted subcar-
riers. Moreover Xtx denotes the column vector for transmitted
symbols from txth transmit antenna, Irx is the column vector
for interferers, Wrx is the column vector for noise, and Ξrxtx is
the matrix containing the channel taps at each m index. The
entries of Ξ are given by
Ξrxtx
=
0
h
rxtx
1
h
rxtx
⎡
⎢
⎢⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
hh
0
[ , ]
n
1
[ , ]
n
0
1
h
rxtx
[ , ]
0
n
1
L
−
[ ,
h
n L
rxtx
0
−
1
]
−
2
]
1
L
−
[ ,
h
n L
rxtx
0
0
h
rxtx
1
h
rrxtx
2[ , ]
n
[ , ]
3
n
0
0
h
rxtx
1
h
rxtx
1
[ , ]
n
[ , ]
2
n
0
1
K
−
[ ,
n L
rxtx
−
1
]
1
K
−
0
[ , ]
n
h
rxtx
0
0
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
(13)
When the channel is assumed to be constant over one
OFDM symbol and the CP is larger than the CIR length, then
h m
rxtx[n, l] is the same for all m’s, making Ξrxtx a circulant
matrix [35]. The multiplication of FΞrxtxFH then results in a
diagonal matrix, and hence no cross-terms between subcarri-
ers exist, that is, no ICI occurs. In this case, h is equivalent to
the first column of Ξ. However, when the channel varies over
an OFDM symbol, then ICI occurs, and for the equalization
the channel at each time sample of OFDM symbol is needed,
that is, at each m samples. For the frequency domain estima-
tion, this requirement translates into the knowledge of the
channel coefficients at each carrier frequency as well as their
cross-terms. The number of unknowns in time domain estima-
tion are KL, whereas the number of unknowns in frequency
domain (the entries of Ψ) are K2. In either case, the number
of unknowns will be higher than the number of equations, and
hence a system of under-determined equations will result in.
Simplifications are needed so that the unknowns in the system
of equations are reduced. Different approaches will be
described in detail in the subsequent sections.
Once the received signals for each transmit antennas are
detected with the help of channel estimation, the reverse
operation at the receiver is performed, that is, they are
demodulated, de-interleaved, and decoded. As it will be seen
later, the information at different stages of decoding process
can be exploited to enhance the performance of channel esti-
mation methods.
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
21
�
y
c
n
e
u
q
e
r
F
y
c
n
e
u
q
e
r
F
Training symbols
Time
(a)
Data symbols
Pilot subcarriers
Time
(b)
Data subcarriers
nFigure 3. Typical training symbols and pilot subcarriers arrangement.
OFDM CHANNEL ESTIMATION TECHNIQUES
There are several basic techniques to estimate the radio chan-
nel in OFDM systems. The estimation techniques can be per-
formed using time or frequency domain samples. These
estimators differ in terms of their complexity, performance,
practicality in applications to a given standard, and the a pri-
ori information they use. The a priori information can be sub-
carriers correlation in frequency [36], time [3], and spatial
domains [37]. Moreover, the transmitted signals being con-
stant modulus [38], CIR length [39], and using a known alpha-
bet for the modulation can also be a priori information [40,
41]. The more the a priori information is exploited, in general
the better the estimates are [42].
For frequency domain channel estimates, MSE is usually
considered as the performance measure of channel estimates,
and it is defined by
MSE = E{|H[n, k] – H^[n, k]|2},
(14)
where H^[n, k] is the estimate of equivalent channel at kth sub-
carrier of nth OFDM symbol. Although MSE is used exten-
sively, sometimes, other measures like BER performance are
also used [43, 44]. BER performance is mainly used when the
performance of OFDM system with the channel estimation
error is to be evaluated [45, 46].
Before introducing the estimation techniques, it is worth-
while to look at the data aided channel estimation in general
and the pilot allocation mechanisms.
DATA AIDED CHANNEL ESTIMATION
In this subsection, we will review commonly used methods in
the data aided channel estimation. Initially, we will consider
the methods developed for SISO-OFDM. ICI is assumed not
to exist and the CIR is assumed to be constant for at least one
OFDM symbol. Hence, Ψ is a diagonal matrix, where each
diagonal element represents the channel between the corre-
sponding received and the transmitted subcarriers. In this
case, for the nth OFDM symbol, the channel given in Eq. 5 at
each subcarrier can be related to Ψ as
H[n, k] = Ψ[k, k].
(15)
Furthermore, the external interference is folded into the noise
with noise statistics being unchanged. With the above assump-
tion, the expression in (12) can be expressed as
Y = diag(X) H + W,
or
Y[n, k] = H[n, k] X[n, k] + W[n, k].
(16)
(17)
Here H and W are the column vectors representing the chan-
nel and the noise at each subcarrier for the nth OFDM sym-
bol, respectively.
In data aided channel estimation, known information to
the receiver is inserted in OFDM symbols so that the current
channel can be estimated. Two techniques are commonly
used: sending known information over one or more OFDM
symbols with no data being sent, or sending known informa-
tion together with the data. The previous arrangement is usu-
ally called channel estimation with training symbols while the
latter is called pilots aided channel estimation (Fig. 3).
Channel estimation employing training symbols periodical-
ly sends training symbols so that the channel estimates are
updated [29]. In some cases training symbols can be sent
once, and the channel estimation can then be followed by
decision directed type channel estimation. The details of the
decision directed will be given later in the article.
In the pilots aided channel estimation, the pilots are multi-
plexed with the data. For time domain estimation, the CIR is
estimated first. The estimate of the CIR are then passed
through a FFT operation to get the channel at each subcarrier
for the equalization in frequency domain. For frequency
domain estimation, the channel at each pilot is estimated, and
then these estimates are interpolated via different methods.
Pilots Allocation for Data Aided Channel Estimation —
For the pilot aided channel estimation, the pilot spacing needs
to be determined carefully. The spacing of pilot tones in fre-
quency domain depends on the coherence frequency (channel
frequency variation) of the radio channel, which is related to
the delay spread. According to the Nyquist sampling theorem,
22
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
�
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
)
s
b
a
(
t
n
e
i
c
i
f
f
e
o
c
n
o
i
t
a
e
r
r
o
C
l
0
10
20
30
40
Subcarrier index
50
60
70
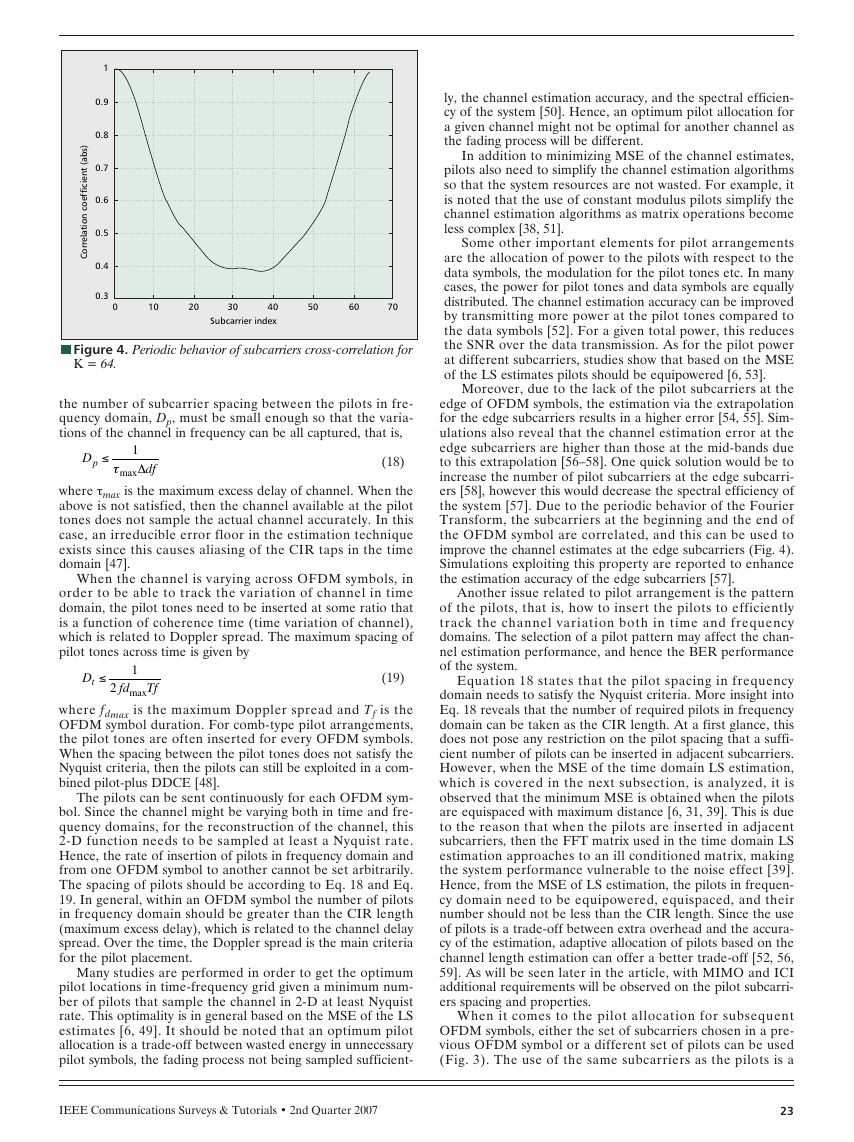
nFigure 4. Periodic behavior of subcarriers cross-correlation for
K = 64.
the number of subcarrier spacing between the pilots in fre-
quency domain, Dp, must be small enough so that the varia-
tions of the channel in frequency can be all captured, that is,
D
p ≤
1
τmax∆
df
(18)
where τmax is the maximum excess delay of channel. When the
above is not satisfied, then the channel available at the pilot
tones does not sample the actual channel accurately. In this
case, an irreducible error floor in the estimation technique
exists since this causes aliasing of the CIR taps in the time
domain [47].
When the channel is varying across OFDM symbols, in
order to be able to track the variation of channel in time
domain, the pilot tones need to be inserted at some ratio that
is a function of coherence time (time variation of channel),
which is related to Doppler spread. The maximum spacing of
pilot tones across time is given by
D
t ≤
1
2 max
fd
Tf
(19)
where fdmax is the maximum Doppler spread and Tf is the
OFDM symbol duration. For comb-type pilot arrangements,
the pilot tones are often inserted for every OFDM symbols.
When the spacing between the pilot tones does not satisfy the
Nyquist criteria, then the pilots can still be exploited in a com-
bined pilot-plus DDCE [48].
The pilots can be sent continuously for each OFDM sym-
bol. Since the channel might be varying both in time and fre-
quency domains, for the reconstruction of the channel, this
2-D function needs to be sampled at least a Nyquist rate.
Hence, the rate of insertion of pilots in frequency domain and
from one OFDM symbol to another cannot be set arbitrarily.
The spacing of pilots should be according to Eq. 18 and Eq.
19. In general, within an OFDM symbol the number of pilots
in frequency domain should be greater than the CIR length
(maximum excess delay), which is related to the channel delay
spread. Over the time, the Doppler spread is the main criteria
for the pilot placement.
Many studies are performed in order to get the optimum
pilot locations in time-frequency grid given a minimum num-
ber of pilots that sample the channel in 2-D at least Nyquist
rate. This optimality is in general based on the MSE of the LS
estimates [6, 49]. It should be noted that an optimum pilot
allocation is a trade-off between wasted energy in unnecessary
pilot symbols, the fading process not being sampled sufficient-
ly, the channel estimation accuracy, and the spectral efficien-
cy of the system [50]. Hence, an optimum pilot allocation for
a given channel might not be optimal for another channel as
the fading process will be different.
In addition to minimizing MSE of the channel estimates,
pilots also need to simplify the channel estimation algorithms
so that the system resources are not wasted. For example, it
is noted that the use of constant modulus pilots simplify the
channel estimation algorithms as matrix operations become
less complex [38, 51].
Some other important elements for pilot arrangements
are the allocation of power to the pilots with respect to the
data symbols, the modulation for the pilot tones etc. In many
cases, the power for pilot tones and data symbols are equally
distributed. The channel estimation accuracy can be improved
by transmitting more power at the pilot tones compared to
the data symbols [52]. For a given total power, this reduces
the SNR over the data transmission. As for the pilot power
at different subcarriers, studies show that based on the MSE
of the LS estimates pilots should be equipowered [6, 53].
Moreover, due to the lack of the pilot subcarriers at the
edge of OFDM symbols, the estimation via the extrapolation
for the edge subcarriers results in a higher error [54, 55]. Sim-
ulations also reveal that the channel estimation error at the
edge subcarriers are higher than those at the mid-bands due
to this extrapolation [56–58]. One quick solution would be to
increase the number of pilot subcarriers at the edge subcarri-
ers [58], however this would decrease the spectral efficiency of
the system [57]. Due to the periodic behavior of the Fourier
Transform, the subcarriers at the beginning and the end of
the OFDM symbol are correlated, and this can be used to
improve the channel estimates at the edge subcarriers (Fig. 4).
Simulations exploiting this property are reported to enhance
the estimation accuracy of the edge subcarriers [57].
Another issue related to pilot arrangement is the pattern
of the pilots, that is, how to insert the pilots to efficiently
track the channel variation both in time and frequency
domains. The selection of a pilot pattern may affect the chan-
nel estimation performance, and hence the BER performance
of the system.
Equation 18 states that the pilot spacing in frequency
domain needs to satisfy the Nyquist criteria. More insight into
Eq. 18 reveals that the number of required pilots in frequency
domain can be taken as the CIR length. At a first glance, this
does not pose any restriction on the pilot spacing that a suffi-
cient number of pilots can be inserted in adjacent subcarriers.
However, when the MSE of the time domain LS estimation,
which is covered in the next subsection, is analyzed, it is
observed that the minimum MSE is obtained when the pilots
are equispaced with maximum distance [6, 31, 39]. This is due
to the reason that when the pilots are inserted in adjacent
subcarriers, then the FFT matrix used in the time domain LS
estimation approaches to an ill conditioned matrix, making
the system performance vulnerable to the noise effect [39].
Hence, from the MSE of LS estimation, the pilots in frequen-
cy domain need to be equipowered, equispaced, and their
number should not be less than the CIR length. Since the use
of pilots is a trade-off between extra overhead and the accura-
cy of the estimation, adaptive allocation of pilots based on the
channel length estimation can offer a better trade-off [52, 56,
59]. As will be seen later in the article, with MIMO and ICI
additional requirements will be observed on the pilot subcarri-
ers spacing and properties.
When it comes to the pilot allocation for subsequent
OFDM symbols, either the set of subcarriers chosen in a pre-
vious OFDM symbol or a different set of pilots can be used
(Fig. 3). The use of the same subcarriers as the pilots is a
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
23
�
widely used pilot arrangement. In such a pilot arrangement,
first the channel between subcarriers is estimated via interpo-
lation in frequency domain. This is followed by interpolation
over OFDM symbols in time domain. In some cases, interpo-
lation can be first performed in time domain, followed by the
frequency domain interpolation. The details of different inter-
polation techniques will be given later in this section.
The analysis of MSE of time domain LS estimation over
several OFDM symbol indicates that for a lower MSE, the
pilots should be cyclically shifted for the next OFDM symbol
[6, 60]. This pilot allocation is similar to those used in DTV
applications, and is similar to the pilot scheme given in Fig.
13. In this pilot allocation scheme, the interpolation is first
performed in frequency domain, followed by the interpolation
in time domain. Similar to the pilot scheme used in DTV, a
hexagonal type pilot scheme is also proposed [61–63]. In both
schemes, different subcarriers are utilized for each OFDM
symbol, and hence the possibility of sticking into terribly fad-
ing subcarriers is eliminated, that is, diversity is exploited.
In addition to the above pilot schemes, different types of
pilot schemes are tested through simulations [56]. The pilots
having more density than the others, those utilizing different
subcarriers over time and at the edge subcarriers are expected
to perform better for channels varying both in time and fre-
quency domains.
The previous pilot allocation schemes were solely based on
the MSE analysis of the channel estimation. In some cases,
other system parameters can also be considered for the pilots
to be used. For example, due to the IFFT block at the trans-
mitter side, PAPR of OFDM systems can be very high. It is
observed that different training symbols (not scattered pilots)
results in different PAPR [64]. Moreover, different scattered
pilot allocation schemes can result in different PAPR when
multiplexed with data. Since the data is random, the optimum
allocation for minimum PAPR will be different for each trans-
mission. However, pre-defined pilot allocation schemes can be
tested for the best PAPR [65]. With such a scheme however,
the information about the pilot scheme needs to be conveyed
to the receiver side, and this reduces the spectral efficiency of
the system.
It is clear from the discussion about the pilot allocation
that a better system performance can be obtained when the
system is adaptive [52, 59, 60, 66]. In this case, the informa-
tion about the channel statistics becomes very critical. The
pilot allocation in the frequency domain requires the delay
spread estimation, whereas the one in over OFDM symbols
(over time evolution) requires Doppler spread estimation. If
these estimates are available, then a pilot scheme using just
the right amount of pilots can yield an acceptable perfor-
mance. If this information is not available, then the pilot
scheme can be designed based on the worst channel condi-
tion, that is, the maximum expected delay and Doppler
spreads. In addition to unknown channel statistics, randomly
generated pilots can be utilized for the reduction of interfer-
ence from adjacent cells. However, it is shown via simulations
that such pilots cause severe degradation in the channel esti-
mation MSE [67].
So far the pilots in the frequency domain are discussed. In
some cases, the estimation can be performed using the data in
time domain, that is, data before the FFT block at the
receivers. Training symbols for this case can be set to all 1’s in
frequency domain that result in an impulse in the time
domain. When this impulse is passed through the channel,
then CIR can be obtained. By careful arrangement of 1’s in
frequency domain, the multiple replicas of the CIR can be
obtained, and these can be improved through noise averaging.
In a similar way, PN sequences superimposed with the data
can be utilized for the channel estimation. In such a case, cor-
relators at the receiver can be used for the expected samples
of the OFDM symbols [68–70]. However, it is shown that
superimposing training with data is not optimal for channel
estimation [71].
Having reviewed the pilot schemes employed in OFDM
systems, it is time to look at the channel estimation tech-
niques. Starting from the methods using the least a priori
information, in this article we will review channel estimation
methods such as LS estimation, ML, transform domain tech-
niques, and LMMSE. Simple interpolation techniques will be
covered along with LS estimation technique.
LS ESTIMATION
Before going into the details of the estimation techniques, it is
necessary to give the LS estimation technique as it is needed
by many estimation techniques as an initial estimation. Start-
ing from system model of SISO-OFDM given in Eq. 17 as[72]
(20)
Y[n, k] = X[n, k]H[n, k] + W[n, k],
the LS estimation of H[n, k] is
ˆHLS[ n,k ]=
Y[n,k ]
X[ n,k ]
= H [n,k ]+
W[ n,k ]
X[ n, k]
.
(21)
In matrix notations,
LS = diag(X)–1Y + diag(X)–1W.
H^
Note that this simple LS estimate for H^
(22)
LS does not exploit
the correlation of channel across frequency carriers and across
OFDM symbols.
The MSE of LS estimation of Eq. 22 is given by [73]
MSE
=
LS
K
SNR
⋅
E
H
(23)
where EH = E{H[n, k]}.
LS method, in general, is utilized to get initial channel esti-
mates at the pilot subcarriers [72], which are then further
improved via different methods.
It is also common to introduce CIR to Eq. 16 to exploit
CIR length for a better performance [21, 74]. In this case, Eq.
16 can be modified as [74]
Y = diag(X)Fh + W
where H = Fh. The LS estimation of Eq. 24 is then
H^ = QLSFH diag(X)HY
where
QLS = (FH diag(X)Hdiag(X)F)–1.
(25)
(26)
The above LS estimation will be referred as time domain LS.
When no assumptions on the number of the CIR taps or
length are made, then the time domain LS reduces to that of
frequency domain, and it does not offer any advantages. How-
ever, with the assumption that there are only L number of
channel taps, which then reduces the dimension of the matri-
ces F and hence Q, an improved performance due to the
noise reduction can be obtained [75, 76]. The resultant LS
estimation has higher computational complexity than the fre-
quency domain LS but the performance increase is the plus
side of the approach. The increase in the performance can be
considered as the exploitation of subcarrier correlation. A
comparison study showed that when the frequency domain LS
also exploits the correlation of the subcarriers, then its perfor-
mance can be that of time domain LS (21). Further compari-
24
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
�
son studies showed that based on the SNR information, either
method can be used [74]. For example if the SNR is low then
the time domain LS can be less accurate as additional filtering
in time domain is based on less accurate CIR length. In this
case, the probability of not accounting for all the taps and dis-
carding some of them are high. However, for other SNR
regions, the time domain LS gives better results as it utilizes a
more accurate CIR length. The use of time domain LS
becomes inevitable when OFDM is combined with MIMO
systems [77]. This will be explored more when channel estima-
tion techniques for MIMO systems are presented.
Similar to the time domain LS, the ML estimate of the
CIR taps for the same system model given in Eq. 24 can be
derived. With the assumption of L channel taps and Np num-
ber of pilot subcarriers, the ML estimate of the channel coef-
ficients is shown to be [58, 78],
H^
HFp)–1Fp
ML = (Fp
H diag(X)HY
(27)
where Fp is Np × L truncated unitary Fourier matrix. In the
above formulation, for the sake of simplicity, it is assumed
that pilots symbols are from PSK constellation and hence
diag(X)Hdiag(X) = IK, and they do not appear in the paren-
thesis for the inverse operation. It can be observed that when
the number of pilots is greater than the channel length and
the noise is AWGN, the time domain LS estimate in Eq. 25 is
equivalent to the ML estimate given in Eq. 27 [58, 79]. Fur-
thermore, it should be noted that the ML estimate given in
(27) makes the assumption about the CIR length, which
improves the performance of the estimation accuracy [80].
Unlike LMMSE channel estimation, both LS and ML are
based on the assumption that the CIR is a deterministic quan-
tity with unknown parameters. This implies that LS and ML
techniques do not utilize the long term channel statistics and
hence are expected to perform worse than the LMMSE chan-
nel estimation method [58]. However, the computational com-
plexity is the main trade-off factor between the two groups of
the channel estimation techniques.
Before introducing the other channel estimation tech-
niques, it is worthwhile to review the methods used for the
training sequences as well as the pilot subcarriers. The corre-
sponding implications on the channel estimation techniques
will also be covered briefly.
CHANNEL ESTIMATION TECHNIQUES IN TRAINING MODE
As mentioned before, in the training mode, all the subcarriers
of an OFDM symbol are dedicated to the known pilots. In
some systems like WLAN or WiMAX, two of the symbols are
reserved for the training. If the training symbols are employed
over two OFDM symbols, for very slowly varying channels, the
channels at two OFDM symbols for the same subcarriers can
be assumed to be the same. In this case, the estimates can be
averaged for further noise reduction [72]. If the noise vari-
ances of the OFDM symbols are different, then Kalman filter-
ing can be used such that noise variances are exploited as
weighting parameters [81].
Once the channel is estimated over the training OFDM
symbols, it can be exploited for the estimation of the channels
of the OFDM symbols sent in between the training symbols.
Depending on the variation of the channel along time, differ-
ent techniques can be utilized.
A very common method is to assume the channel being
unchanged between OFDM training symbols [23, 28–30, 69].
In this method, the channel that is estimated at training sym-
bols is used for the subsequent symbols until a new training
sequence is received. The channel is then updated by using
the new training sequence, and the process continues. In fact,
this is one of the algorithms employed for IEEE 802.11a/b/g
and fixed WiMAX systems. However, these approaches intro-
duce an error floor for non-constant channels, that is, outdoor
channels. The highest performance degradation occurs at the
symbols farthest from the training symbols. For video trans-
mission systems, the critical information can be sent over the
symbols closer to the training symbols, while non-critical
information can be sent over those farther from the training
symbols [29, 30]. It is observed that such an arrangement can
improve the performance without increasing the number of
training blocks. However, for systems requiring equal priority
packets like data networks, such an approach cannot be taken.
In this case satisfactory results can be obtained by increasing
the rate at which the training symbols are sent at the expense
of system efficiency.
For the fast varying channels, interpolation methods can be
utilized in time domain. Interpolating the channel linearly
between the training symbols is one simple solution [59, 72,
82]. The disadvantage with such an approach is the latency
introduced in the system [83]. Indeed, if the system can toler-
ate more latency, then the channel estimation for non-training
OFDM symbols can be improved by higher order polynomials
[66, 84, 85].
CHANNEL ESTIMATION TECHNIQUES IN PILOT MODE
In the pilot mode, only few subcarriers are used for the initial
estimation process. Depending on the stage where the estima-
tion is performed, estimation techniques will be considered
under time and frequency domains techniques.
In frequency domain estimation techniques, as a first step,
CFR for the known pilot subcarriers is estimated via (22).
These LS estimates are then interpolated/extrapolated to get
the channel at the non-pilot subcarriers. The process of the
interpolation/extrapolation can be denoted as
H^ = QH^LS
(28)
where Q is the interpolation/extrapolation matrix. The goal of
the estimation technique is to obtain Q with lower computa-
tional complexity but at the same time is to achieve higher
accuracy for a given system. In this subsection, the calculation
of matrix Q for simple interpolation techniques will be dis-
cussed.
Piecewise Linear Interpolation — Two of the simplest ways
of interpolation are the use of piecewise constant [86] and lin-
ear interpolation [22, 84, 87, 88]. In the piecewise constant
interpolation, the CFR between pilot subcarriers is assumed to
be constant, while in piecewise linear interpolation the channel
for non-pilot subcarriers is estimated from a straight line
between two adjacent pilot subcarriers. Mathematically, for
piecewise constant interpolation, Q is a matrix consisting of
columns made up from shifted versions of the column vector
c = … …
,
,
1 0
[ , ,
,
1 1
D
p
T
, ] ,
0
where Dp is the spacing of the pilots. For the the piecewise
linear interpolation, Q consists of coefficients that are a func-
tion of the slope of the line connecting two pilot subcarriers
and the distance of the pilots to the subcarrier for which the
channel is to be estimated.
In the first method, acceptable results can be obtained if
the CFR is less frequency selective or the CIR maximum
excess delay is very small. Such a constraint makes the CFR at
the subcarriers very correlated that CFR at a group of subcar-
riers can be assumed to be the same.
IEEE Communications Surveys & Tutorials • 2nd Quarter 2007
25
�














 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc