基于仿真优化的公交站点泊位分配问题研究 .pdf

发布时间：2022-06-14 发布人：admin 分类：说明书资料大小：0.64M 资料格式：pdf 举报版权申诉

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第1页.png

第1页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第2页.png

第2页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第3页.png

第3页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第4页.png

第4页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第5页.png

第5页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第6页.png

第6页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第7页.png

第7页 / 共9页

c118b806-3a06-4ce1-95f9-8c755169e5e1.pdf-第8页.png

第8页 / 共9页

文本预览

中国科技论文在线 http://www.paper.edu.cn 基于仿真优化的公交站点泊位分配问题研究郑阳阳，朱宁** （天津大学管理与经济学部）摘要：公交站点的通行能力是限制公交系统通行能力提高的主要瓶颈。公交站点的泊位数量设置对其通行能力有着直接影响。在公交系统运行中，线路中的不同站点运行状态差异大且相互影响，对站点泊位数量的设置存在干扰。本文考虑线路中不同站点的服务强度、不确定的车辆服务时间和站间行驶时间、站点采用的超车机制等多重因素，以公交车辆与乘客的平均延迟时间为目标函数，利用仿真优化技术对整条线路连续多个站点的泊位数量进行优化，获取最优泊位数量分配方案。相较于实际中站点泊位分配情况，优化后线路中的公交车辆与乘客的平均延迟时间降低 14%以上，研究结果对线路中公交站点泊位数量设置与通行能力的提高提供了借鉴意义。关键词：公交站点通行能力；泊位数量优化；遗传算法；公交仿真系统中图分类号：U121 Research on Berth Allocation of Bus Station Based on Simulation Optimization Zheng Yangyang, ZHU Ning (College of Management and Economics of Tianjin University) Abstract: The capacity of bus stop is the main bottleneck to limit that of bus transit capacity. Berth’s quantity at the bus stop has a direct impact on its capacity. When transport system is operating, stations in the line affect each other, which will account for the quantity of berths in the stations. Considering various factors such as service intensity, uncertain service time and inter-stations travel time as well as the overtaking mechanism adopted by the stations, this paper takes average delay time of bus vehicles and passengers in system as the objective function, then optimization technology based on simulation are used to obtain an optimal berth allocation scheme for a bus line. Compared with the actual berth allocation, the optimal result can greatly reduce the delay time of the bus and passengers by more than 14%. The research can provide reference for the berth allocation optimization for transit department. Key words: bus stop capacity; berth quantity optimization; genetic algorithm; bus simulation system 5 10 15 20 25 30 0 引言 35 优先发展公共交通系统成为解决城市交通拥堵问题的重要措施。其中公交车系统因成本低、覆盖范围广，在公共交通系统中占有重要地位。2017 年，北京中心城公共交通出行中，公交车出行高达 50.6%[1]。发展公交车系统，关键是提高系统整体的通行能力。研究发现，公交车运行时，在交叉口平均延误时间为 15s，在站点处则长达 45-90s。因此公交站点成为限制公交系统通行能力提高的主要瓶颈[2]。 40 关于提高公交站点的通行能力的研究，主要集中在对车辆施加站内停靠时间控制[3，4]、跳站[5]等实时控制策略方面，调节车辆规律性到站，避免站内拥堵。但策略的制定对技术依赖度高，也会影响后续车辆的服务时间和到达率，具有一定的负面性。W Gu 等[6]指出站点作者简介：郑阳阳（1993-），硕士研究生，主要研究方向：公交系统的仿真与优化通信联系人：朱宁（1984-），男，副教授，硕导，主要研究方向：基于大数据的交通与物流系统分析与建模. E-mail: zhuning@tju.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 的通行能力会受到服务时间、车头时距变化的影响，与泊位数量并非成正相关；后指出根据车辆停靠时间变化，合理采取限制性的超车行为能提高站点的通行能力[7]。 45 此外，合理设置公交站点泊位数量也是提高公交站点通行能力的有效措施。站点泊位数量少，无法有效容纳到站车辆造成排队现象；泊位数量多，车辆在站内交互增多且空间浪费。国内学者提出了单个公交站点泊位数量计算方法[8，9]，柏海舰[10]、张旭等[11]分别利用排队论原理提出新的站点通行能力和泊位数量计算模型，实现对站点处泊位的优化设计。但是公交线路通过的公交站点较多，站点间运行状态相互影响，已有研究具有一定的局限性。 50 目前我国多数城市公交站点的泊位数量是不确定的，车辆到站停靠较随意，排队、阻塞现象发生频率高，公交线路经过的站点数量不断增加。因此，对整条公交线路的站点泊位数量进行优化，减少系统内时间延迟是很有必要的。本文考虑线路中连续多个站点之间的相互影响，结合站内服务强度、不确定的站间行驶时间、站点采取的超车机制等因素，利用遗传算法与蒙特卡罗仿真，以最小化线路中公交车 55 辆与乘客的延迟时间为目标，对线路中连续站点的泊位数量分配进行优化，为提高线路的通行能力提供参考建议。 1 问题描述基于仿真优化的公交站点泊位分配问题可描述如下：系统内主线路车辆发出后沿途依次经过个公交站点，到达每个站点后进行进站、选择泊位停靠、服务乘客、出站离开等操作。 60 在该过程中，存在进程延迟的情况：当站内所有泊位被占用或上游泊位存在服务车辆阻碍其他车辆进入下游泊位时，站外车辆需要排队等待；当车辆出站时，前方存在未驶离车辆，需在站内多停留一段时间。三种情况均会导致车辆不同程度的延迟，示意图依次如下图 1-3 所示。图 1 泊位不足情况图 2 无法超车进站图 3 无法超车出站 Fig. 1 Insufficient berths 在上述过程中，站点内泊位数量是导致车辆延迟的直接因素，也受到多种因素的间接影 Fig. 2 No overtaking-in Fig. 3 No overtaking-out 65 响。每个站点因服务多条线路，其服务强度由其他线路车辆的到站率、服务时间分布特征决定，反应出站点处车辆排队或相互阻塞发生概率的大小。主线路车辆运行速度受到路况等条件的干扰，无法按照规定时间到达每个站点，增加了公交系统的不确定性。同时乘客随机到站导致车辆服务时间波动大，车辆在站内相互阻塞的概率增加。并且，研究发现在公交站点处采取不同的超车机制对站点车辆延迟时间[12]会产生不同的影响。因此，本文采用 B Bian[12] 70 等提出的包括禁止超车进出站、允许超车进站禁止超车出站、禁止超车进站允许超车出站、允许超车进出站四种超车机制，全面考虑不同超车机制下线路站点的泊位分配情况。当车辆连续经过多个公交站点后，延迟时间依次累加。所以，现以最小化系统内车辆与乘客的平均延迟时间为目标，利用优化仿真技术获取线路中连续多个公交站点的最优泊位数 - 2 -

中国科技论文在线 http://www.paper.edu.cn 量分配方案，以提高公交系统整体的通行能力。 75 2 模型描述 2.1 公交系统仿真模型公交系统是一个复杂系统，其内部要素的状态和相互作用受到诸多随机因素的影响，所以其状态难以用数学模型进行精确表达，通过现场做实验探讨其内在规律困难度也极大。因此本文借鉴目前使用广泛的新型仿真平台 PASSION(Parallel Stop Simulation)[13,14]的优势，考 80 虑车辆之间、车辆与乘客之间的交互以及其他影响因素，建立公交系统仿真模型，用以模拟车辆、站点的运行状况。其整体流程框图如图 4 所示。图 4 公交系统仿真模型流程图 Fig.4 Flow diagram of bus system simulation model 85 2.2 模型假设为了使研究问题简化清晰，结合公交系统运行实际情况，对公交系统仿真模型做出以下假设：（1）将每个站点服务的其他线路看作对应此站点的一条整体线路，该整体线路车辆的到 - 3 -

中国科技论文在线 http://www.paper.edu.cn 站、服务乘客过程均相互独立且服从泊松分布[12，15]； 90 （2）主线路的乘客到达站点的过程服从泊松分布；（3）主线路车辆的车速服从正态分布，且同时处于连续的两个站点间的车辆速度是相同的；（4）不考虑车容量的限制，车辆到站后使用允许停靠的相对下游泊位。 2.3 模型变量与参数 95 表 1 模型变量符号与含义变量名称变量符号释义 Tab. 1 Notation of the variables of model 主公交线路中的公交车，主公交线路中的公交站点，公交车在站点处的到达时间公交车在站点处的离开时间公交车在站点处的服务时间公交车在站点与站点的行驶时间分别为公交车在站点处的总延迟时间,进站延迟与出站延迟公交车在一次运行中的总延迟时间，在站点处公交车的上车乘客数在站点处公交车的下车乘客数在站点处公交车上的乘客总数公交车在站点处发生延迟时对该车车内乘客造成的时间延迟公交车在一次运行中对该车车内乘客造成的总时间延迟，表 2 模型参数符号与含义 Tab. 2 Notation of the parameters of model 参数名称参数符号释义主公交线路中的公交车总数主公交线路中的公交站点系统内乘客总数乘客的平均上车时间（s/人）乘客的平均下车时间（s/人）站点处乘客的到达率（人 /s）站点处其他线路车辆的到达率（人 /s）站点处对其他线路车辆的服务率（人 /s）仿真模型内部变量之间的关系如下所示： 100 假设公交车辆有两个门，前门用于乘客上车，后门用于乘客下车，车辆在站内提供服务时因开关门、加减速等需要一段固定时间，所以主线路车辆在站点的服务时间等于乘客 - 4 - i1,2,...,iMj1,2,...,jNijAijijDijijSijijTi1jj''',,ijijijdddijidi1NiijjddijUjiijVjiijPjiijPdijiPdi1NiijiPdPdMNPabjjjjjjij

中国科技论文在线 http://www.paper.edu.cn 总上车时间与总下车时间中的最大值与固定时间的和： (1) 车辆在站点的到达时间等于上一站点的离开时间加上两站点之间的行驶时间：车辆离开站点的时间等于到达时间与进站延迟时间、服务时间与出站延迟时间的和： (2) (3) 105 车辆到达站点后，车内乘客随机下车，等待上车的乘客数是在车辆离开之后，逐渐到站的乘客数量总和，约为：车辆离开站点后，车内的乘客数为： (4) (5) 车辆到达站点后，若泊位被服务车辆占用，则会发生排队现象，等待服务车辆离开，延迟进站；当车辆完成服务后，若车辆前方的泊位存在未驶离车辆，延迟出站，此 110 时车辆总的延迟时间为：车辆在站点进站、出站发生延迟时，对车内乘客造成的延迟为： (6) (7) 2.4 目标函数在该公交仿真系统中，多种因素致使车辆无法及时进站、出站，对车辆和车内乘客均造成延迟。本文将线路途经的连续多个站点作为研究对象，探究使系统内车辆与乘客的平均延 115 迟时间最小的泊位数量分配方案。将系统内车辆与乘客的平均延迟时间作为目标函数，表达式如下： 2.5 优化算法 (8) 针对该优化问题，复杂因素增加了求解难度，本文利用遗传算法进行求解。根据《美国道路通行能力手册》(Highway Capacity Manual, HCM)中公交站点通行能力公式[16]，站内泊 120 位数量的增加会导致泊位利用率下降，当泊位数量增加至 4 或 5 时，站点通行能力仅增加 20%和 5%，所以适宜数量为 1~3 个[13],因此该问题的解空间大小为。但根据实际经验，当站点的服务强度较大时，单个泊位将大幅增加站点处排队发生的概率，所以对站点泊位数进行初判断可有效减少搜索空间的大小。此外，现实中公交站点的泊位数量默认为 2 个， - 5 - max(,)4ijijijSbUaVij1ijijijADTij'''ijijijijijDAdSdij1()ijijijjUDDij1ijijijijPPUViji'''ijijijdddij'''ijijijijijPdPdPd1111minMNMNijijijijdPdWMP3NN

中国科技论文在线 http://www.paper.edu.cn 一条线路途经个站点，泊位总数即为个。现将优化过程看作重新分配个泊位到站点中， 125 整个遗传算法的使用过程如下： (1) 构建初始解：设置种群大小为，迭代次数，交叉率和变异率。设置迭代次数 , 利用随机数生成种群中的染色体。计算每个站点因其他线路车辆造成的站点服务强度 ,如果，将泊位数随机设置 2~3，否则为 1~3，依此为每个站点设置泊位数后形成染色体，每一条染色体代表一个分配方案，利用公交车仿真系统获取 130 每条染色体对应的目标函数值，其中设置为 0.6； (2) 交叉：将种群内个体进行两两配对，为每对生成随机数，选择其中的染色体对进行双切点交叉，挑选其中满足泊位总数约束的个体； (3) 变异:为种群内每个个体生成随机数，选择其中的染色体进行换位变异； (4) 评估与选择：根据仿真系统获取的目标函数值，构建轮盘赌概率，选择个个体构建下 135 一代种群； (5) 停止规则：如果，则停止迭代，输出最优解及对应的染色体；否则，，转步骤（1）. 3 算例实验 3.1 仿真实验参数设置 140 主线路途经 18 个站点，发车的时间间隔为 5min，车辆的速度均值为 7.25m/s，标准差为 4.5，主线路乘客的到站率、站点的其他线路车辆到达率、服务率如表 4 所示。种群大小与迭代次数均为 50，交叉概率为 0.5，变异概率为 0.02。假设进站、出站过程中允许超车为 1，禁止超车为 0，针对禁止超车进出站、禁止超车进站允许超车出站、允许超车进站禁止超车出站、允许超车进出站四种站点超车机制，分别简称为“00” ，“01” ，“10” ，“11”。结 145 合系统中站点与车辆的参数设置，依此在四种不同的超车机制下，获取对应的最优方案。 3.2 四种超车机制下线路在泊位上的分配方案在现实中，站点处为避免车辆超车影响相邻车道的车辆和站点周围人流，多采取“00” 机制，即禁止公交车辆超车进出站。研究表明[7]，车站处服务强度和车辆服务时间变化大时，采取限制性超车机制可以提高站点的通行能力。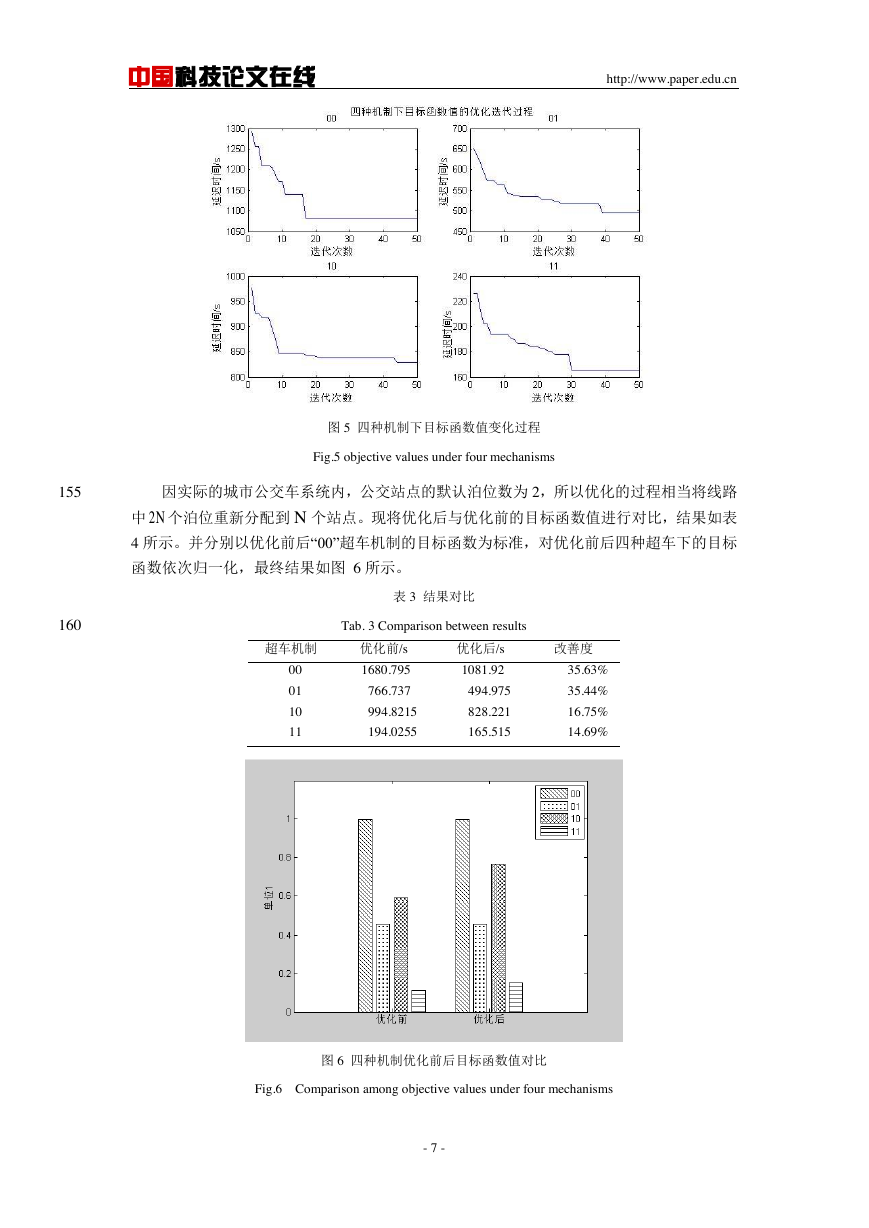本文在不确定站间行驶时间、服务时间与站 150 点服务强度等多种因素影响下，分别获得了“00” ，“01” ，“10” ，“11”四种超车机制下的泊位数量优化方案，优化中四种机制下目标函数值变化过程如图 5 所示。 - 6 - 2N2NnGcPmP1g,1,2...jjjjNjcc[0,1]crccrP[0,1]mrccrPngG1gg

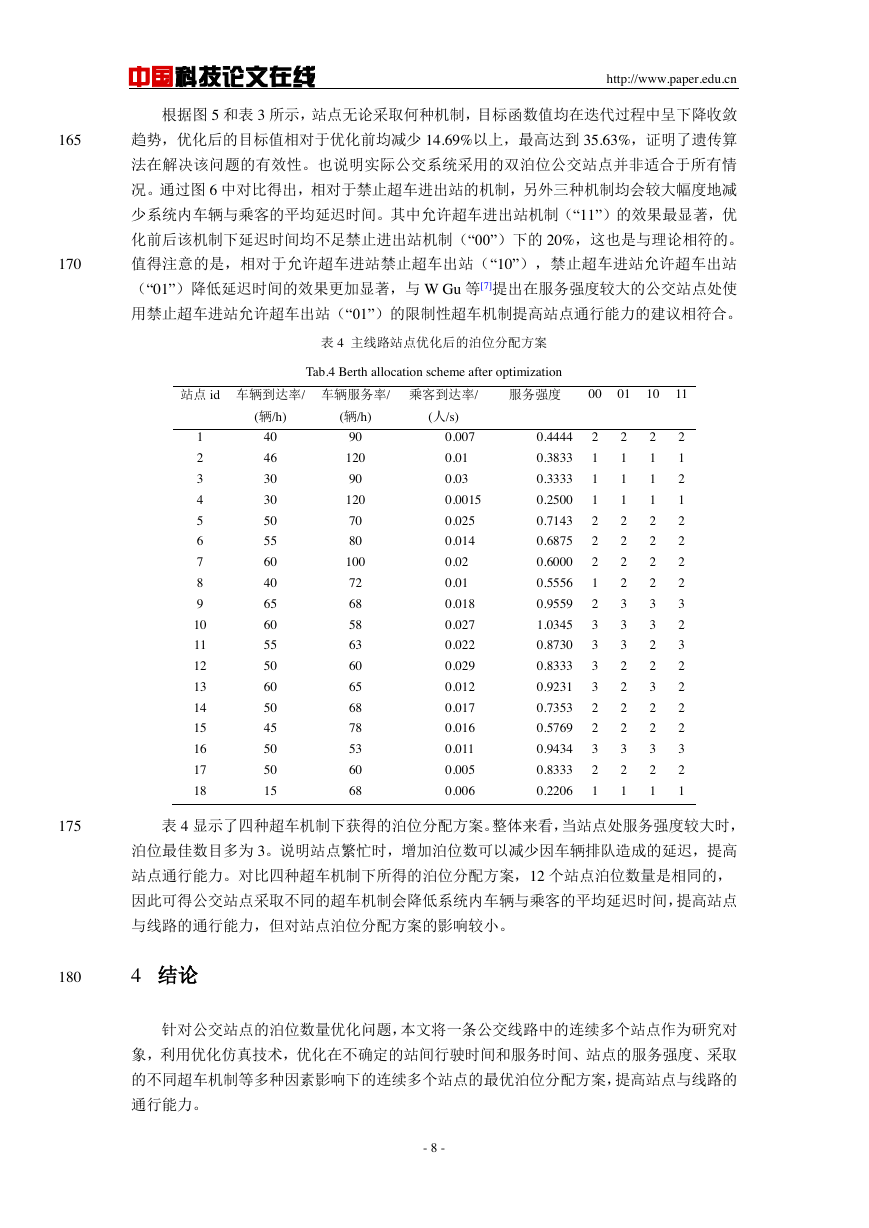
中国科技论文在线 http://www.paper.edu.cn 图 5 四种机制下目标函数值变化过程 Fig.5 objective values under four mechanisms 155 因实际的城市公交车系统内，公交站点的默认泊位数为 2，所以优化的过程相当将线路中个泊位重新分配到个站点。现将优化后与优化前的目标函数值进行对比，结果如表 4 所示。并分别以优化前后“00”超车机制的目标函数为标准，对优化前后四种超车下的目标函数依次归一化，最终结果如图 6 所示。表 3 结果对比 160 Tab. 3 Comparison between results 超车机制 00 01 10 11 优化前/s 1680.795 766.737 994.8215 194.0255 优化后/s 1081.92 494.975 828.221 165.515 改善度 35.63% 35.44% 16.75% 14.69% 图 6 四种机制优化前后目标函数值对比 Fig.6 Comparison among objective values under four mechanisms - 7 - 2NN

中国科技论文在线 http://www.paper.edu.cn 根据图 5 和表 3 所示，站点无论采取何种机制，目标函数值均在迭代过程中呈下降收敛 165 趋势，优化后的目标值相对于优化前均减少 14.69%以上，最高达到 35.63%，证明了遗传算法在解决该问题的有效性。也说明实际公交系统采用的双泊位公交站点并非适合于所有情况。通过图 6 中对比得出，相对于禁止超车进出站的机制，另外三种机制均会较大幅度地减少系统内车辆与乘客的平均延迟时间。其中允许超车进出站机制（“11”）的效果最显著，优化前后该机制下延迟时间均不足禁止进出站机制（“00”）下的 20%，这也是与理论相符的。 170 值得注意的是，相对于允许超车进站禁止超车出站（“10”），禁止超车进站允许超车出站（“01”）降低延迟时间的效果更加显著，与 W Gu 等[7]提出在服务强度较大的公交站点处使用禁止超车进站允许超车出站（“01”）的限制性超车机制提高站点通行能力的建议相符合。表 4 主线路站点优化后的泊位分配方案 Tab.4 Berth allocation scheme after optimization 站点 id 车辆到达率/ 车辆服务率/ 乘客到达率/ 服务强度 00 01 10 11 (辆/h) (辆/h) (人/s) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 40 46 30 30 50 55 60 40 65 60 55 50 60 50 45 50 50 15 90 120 90 120 70 80 100 72 68 58 63 60 65 68 78 53 60 68 0.007 0.01 0.03 0.0015 0.025 0.014 0.02 0.01 0.018 0.027 0.022 0.029 0.012 0.017 0.016 0.011 0.005 0.006 0.4444 0.3833 0.3333 0.2500 0.7143 0.6875 0.6000 0.5556 0.9559 1.0345 0.8730 0.8333 0.9231 0.7353 0.5769 0.9434 0.8333 0.2206 2 1 1 1 2 2 2 1 2 3 3 3 3 2 2 3 2 1 2 1 1 1 2 2 2 2 3 3 3 2 2 2 2 3 2 1 2 1 1 1 2 2 2 2 3 3 2 2 3 2 2 3 2 1 2 1 2 1 2 2 2 2 3 2 3 2 2 2 2 3 2 1 175 表 4 显示了四种超车机制下获得的泊位分配方案。整体来看，当站点处服务强度较大时，泊位最佳数目多为 3。说明站点繁忙时，增加泊位数可以减少因车辆排队造成的延迟，提高站点通行能力。对比四种超车机制下所得的泊位分配方案，12 个站点泊位数量是相同的，因此可得公交站点采取不同的超车机制会降低系统内车辆与乘客的平均延迟时间，提高站点与线路的通行能力，但对站点泊位分配方案的影响较小。 180 4 结论针对公交站点的泊位数量优化问题，本文将一条公交线路中的连续多个站点作为研究对象，利用优化仿真技术，优化在不确定的站间行驶时间和服务时间、站点的服务强度、采取的不同超车机制等多种因素影响下的连续多个站点的最优泊位分配方案，提高站点与线路的通行能力。 - 8 -

分享到：

赞收藏

资料库

基于仿真优化的公交站点泊位分配问题研究 .pdf

相关推荐

开发技术

热门标签

最新资料