logo资料库

单级倒立摆的模糊控制以及在MATLAB中的仿真1.doc

发布时间：2022-06-16 发布人：admin 分类：说明书 资料大小：3.32M 资料格式：doc 举报 版权申诉
第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
资料共16页，剩余部分请下载后查看
    单级倒立摆的模糊控制以及在 MATLAB 中的仿真 姓 学 院 名： 号： 系： 韦 盛 P081613346 电气工程学院 专业班级： 电气工程及其自动化 指导教师： 刁晨 日 期： 2011 年 11 月 11 日
    单级倒立摆的模糊控制以及在MATLAB中的仿真 摘要 倒立摆系统是一个典型的多变量、非线性、强藕合和快速运动的自然不稳定系统。因此 倒立摆在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重 要的现实意义，相关的科研成果己经应用到航天科技和机器人学等诸多领域。 本文围绕一级倒立摆系统，采用模糊控制理论研究倒立摆的控制系统仿真问题。仿真的 成功证明了本文设计的模糊控制器有很好的稳定性。主要研究工作如下： （1)使用了牛顿力学和Lagrange方程对倒立摆进行数学建模，推导出倒立摆系统传递函数 和状态空间方程。 （2)分析了模糊控制理论的数学基础，对模糊控制的方法进行了研究：介绍了模糊子集、 模糊关系和模糊推理等相关知识。 （3)介绍了如何利用Simulink建立倒立摆系统模型，特别是利用Mask封装功能，使模型更 具灵活性，给仿真带来很大方便。 （4)进行一级倒立摆系统的控制器设计与仿真。通过matlab的Simulink实现倒立摆模糊控 制系统的仿真。说明仿真结果的趋向。 关键词： 倒立摆 模糊控制 仿真 MATLAB 第一章 绪论 1．1 倒立摆系统的重要意义 倒立摆系统是研究控制理论的一种典型实验装置，具有成本低廉，结构简单，物理参 数和结构易于调整的优点，是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不 稳定系统。在控制过程中，它能有效地反映诸如可镇定性、鲁棒性、随动性以及跟踪等许多 控制中的关键问题，是检验各种控制理论的理想模型。迄今人们已经利用经典控制理论、现 代控制理论以及各种智能控制理论实现了多种倒立摆系统的控制稳定。倒立摆主要有：有悬 挂式倒立摆、平行倒立摆、环形倒立摆、平面倒立摆；倒立摆的级数有一级、二级、三级、 四级乃至多级；倒立摆的运动轨道可以是水平的，也可以是倾斜的：倒立摆系统己成为控制 领域中不可或缺的研究设备和验证各种控制策略有效性的实验平台。同时倒立摆研究也具有 重要的工程背景：如机器人的站立与行走类似双倒立摆系统；火箭等飞行器的飞行过程中， 其姿态的调整类似于倒立摆的平衡等等。因此对倒立摆控制机理的研究具有重要的理论和实 践意义。 1．2 倒立摆系统的控制方法
    自从倒立摆产生以后，国内外的专家学者就不断对它进行研究，其研究主要集中在下面 两个方面： （1）倒立摆系统的稳定控制的研究 （2）倒立摆系统的自起摆控制研究 而就这两方面而言，从目前的研究情况来看，大部分研究成果又都集中在第一方面即倒 立摆系统的稳定控制的研究。目前，倒立摆的控制方法可分如下几类： (1)线性理论控制方法 将倒立摆系统的非线性模型进行近似线性化处理获得系统在平衡点附近的线性化模型， 然后再利用各种线性系统控制器设计方法得到期望的控制器。如1976年Mori etc的把倒立摆 系统在平衡点附近线性化利用状念空间的方法设计比例微分控制器。1980年，Furuta etc 基于线性化方法，实现了二级倒立摆的控制。1984年，Furuta首次实现双电机三级倒立摆实 物控制。1984年，wattes研究了LQR(Linear Quadratic Regulator)方法控制倒立摆。这类 方法对一、二级的倒立摆(线性化后误差较小、模型较简单)控制时，可以解决常规倒立摆的 稳定控制问题。但对于像非线性较强、模型较复杂的多变量系统(三、四级以及多级倒立摆) 线性系统设计方法的局限性就十分明显了。 （2）预测控制和变结构控制方法 由于线性控制理论与倒立摆系统多变量、非线性之间的矛盾使人们意识到针对多变量、 非线性对象，采用具有非线性特性的多变量控制解决多变量、非线性系统的必由之路。人们 先后开展了预测控制、变结构控制和自适应控制的研究。预测控制是一种优化控制方法，强 调实模型的功能而不是结构。变结构控制是一种非连续控制，可将控制对象从任意位置控制 到滑动曲面上，仍然保持系统的稳定性和鲁棒性，但是系统存在颤抖。预测控制、变结构控 制和自适应控制在理论上有较好的控制效果，但由于控制方法复杂，成本也高，不易在快速 变化的系统上实时实现。 (3)智能控制方法 在倒立摆系统中用到的智能控制方法主要有神经网络控制、模糊控制、仿人智能控制、 拟人智能控制和云模型控制等。利用神经网络的自适应能力、并行处理和高度鲁棒性，采用 神经网络方法设计的控制系统将具有更快的速度、更强的适应能力和更强的鲁棒性。但是神 经网络控制方法存在的主要问题是缺乏一种专门适合于控制问题的动态神经网络，而且多层 网络的层数、隐层神经元的数量、激发函数类型的选择缺乏指导性原则等。 拟人智能控制 模糊控制、神经网络控制等智能控制理论的问世，促进了当代自动控 制理论的发展。然而，基于这些智能控制理论所设计的系统往往需要庞大的知识库和相应 的推理机，不利于实现实时控制。这又阻碍了智能控制理论的发展，因此又有学者提出了一 种新的理论一拟人控制理论。 仿人智能控制仿人智能控制的基本思想是通过对人运动控制的宏观结构和手动控制行
    为的综合模仿，把人在控制中的“动觉智能”模型化，提出了仿人智能控制方法。研究结果 表明，仿人智能控制方法解决复杂、强非线性系统的控制具有很强的实用性。 云模型控制利用云模型实现对倒立摆的控制，用云模型构成语言值，用语言值构成规则， 形成一种定性的推理机制。这种拟人控制不要求给出被控对象精确的数学模型，仅仅依据人 的经验、感受和逻辑判断，将人用自然语言表达的控制经验，通过语言原子和云模型转换到 语言控制规则器中，就能解决非线性问题和不确定性问题。 鲁棒控制方法---鲁棒控制的研究始于20世纪50年代，是一种解决非线性、复杂性和不 确定性的工具，发展方向是面向那些不确定因素变化范围大和稳定裕度小的对象。但是，鲁 棒控制系统的设计要由高级专家完成。一旦设计成功，就不需太多的人工干预。另一方面， 如果要升级或作重大调整，系统就要重新设计。 1.3 论文的主要工作 本论文的主要工作是研究了直线一级倒立摆系统的模糊控制问题，用Matlab和Simulink 对一级倒立摆模糊控制系统进行了仿真，验证了设计的可行性。具体内容如下： （1）论述了一级倒立摆数学建模方法，推导出他们的微分方程，以及线性化后的状态方 程。 （2）讨论了单级倒立摆系统的模糊控制方法和操作步骤。 （3）用Simulink实现了单级倒立摆模糊控制仿真系统，分别给出一级倒立摆系统控制量 的响应曲线。通过仿真说明控制器的有效性和实现性。 （4）对论文的工作进行总结和下一步工作的展望。 第二章 倒立摆的建模 本章研究倒立摆系统的数学模型推导。 系统建模可以分为两种：机理建模和实验建模。实验建模就是通过在研究对象上加上一 系列的研究者事先确定的输入信号，激励研究对象并通过传感器检测其可观测的输出，应用 数学手段建立起系统的输入和输出之间的关系。机理建模就是在了解研究对象的运动规律基 础上，通过物理、化学的知识和数学手段建立起系统内部的输入一状态关系。对于倒立摆系 统，由于其本身是自不稳定的系统，实验建模存在一定的困难。但是经过小心的假设忽略掉 一些次要的因素后，倒立摆系统就是一个典型的运动的刚体系统，可以在惯性坐标系内应用 经典力学理论建立系统的动力学方程。下面我们采用其中的牛顿一欧拉方法建立直线型一级 倒立摆系统的数学模型。 2.1 一级倒立摆的数学模型 在忽略了空气阻力，各种摩擦之后，可以将直线一级倒立摆系统抽象成小车和匀质杆组
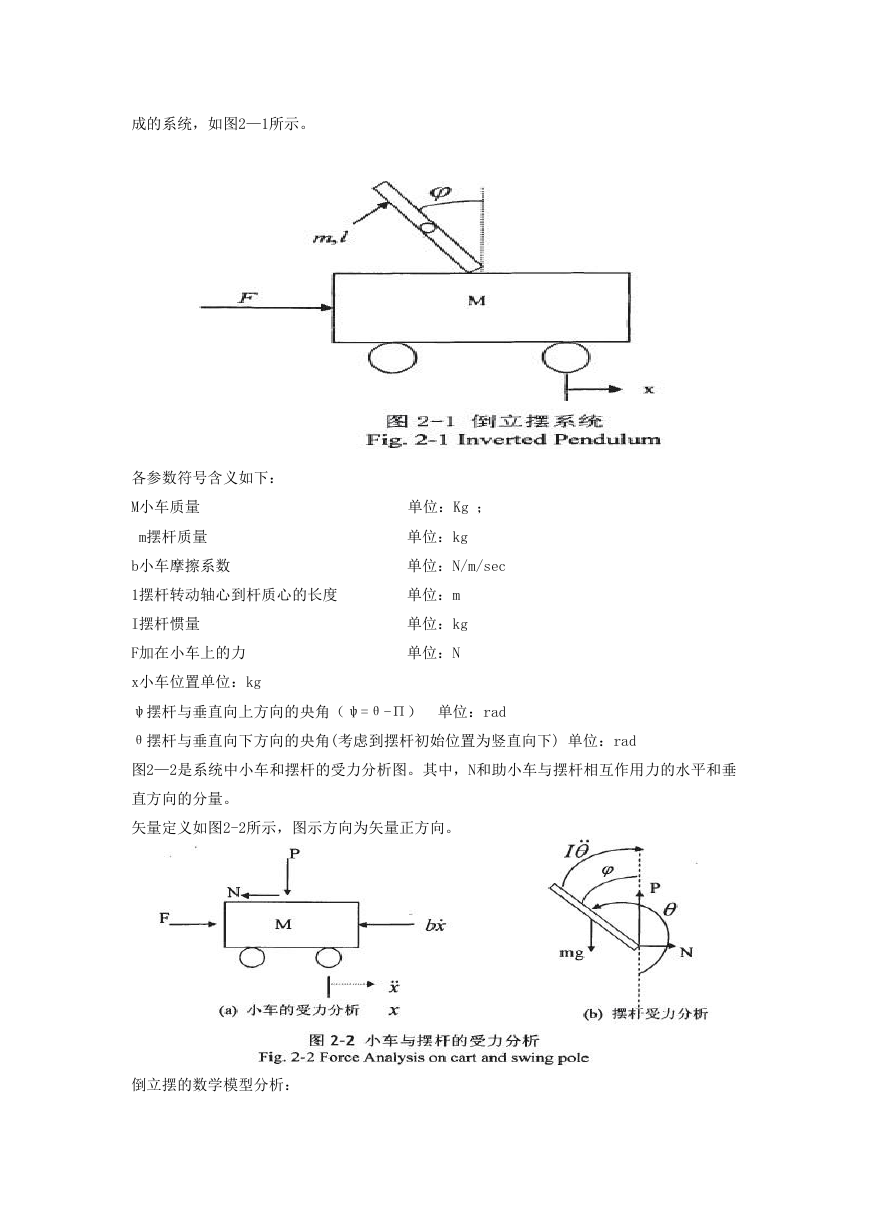
    成的系统，如图2—1所示。 各参数符号含义如下： M小车质量 m摆杆质量 b小车摩擦系数 1摆杆转动轴心到杆质心的长度 I摆杆惯量 F加在小车上的力 x小车位置单位：kg 单位：Kg ； 单位：kg 单位：N/m/sec 单位：m 单位：kg 单位：N ψ摆杆与垂直向上方向的央角（ψ=θ-Π） 单位：rad θ摆杆与垂直向下方向的央角(考虑到摆杆初始位置为竖直向下) 单位：rad 图2—2是系统中小车和摆杆的受力分析图。其中，N和助小车与摆杆相互作用力的水平和垂 直方向的分量。 矢量定义如图2-2所示，图示方向为矢量正方向。 倒立摆的数学模型分析：
    根据图 2-2 所示的倒立摆系统简图，设计和分析其模糊控制器。下面给出了该系统的微 分方程（Kailaith，1980；Craig，1986）  2 dml  m  lg 2 dt   2 sin      tu （1） 这里 m 是摆杆的质量，l 是摆长，是从垂直方向上的顺时针偏转角，=u（t）为作用于 杆的逆时针扭矩【u（t）是控制作用】,t 是时间，g 是重力加速度常数。 假设 x 1    x , 2 d  dt 为状态变量，有等式（1）给出的非线性系统的的状态空间表 达式为 xd 1 dt  x 2 xd 2 dt   lg  sin  x 1    1   tuml 2 从所周知，当偏转角很小时，有 sin（）=，这里所测得用弧度表示。由此式可将 状态空间表达式线性化，并得 xd 1 dt  x 2 xd 2 dt    xlg 1  1   tuml 2 2  若所测 1x 用度表示， 2x 用每秒度表示，当取 l=g 和 m= 180  g 时，线性离散时间状态空 2 间表达式可用矩阵查分方程表式  kx 1  1    kx 1   kx 2  kx 2  1    kx 1    kx 2   ku 在此问题中，设上述两变量的论域为   2  x 1   2 和  5 rad s  x 2  5 rad s ,则设计步 骤为 第 1 步。首先，对 1x 在其论域上建立三个隶属度函数，即如图 1 所示的正值（P）、零 （Z）和负值（N）。然后，对 2x 在其论域上亦建立 3 个隶属度函数，即图 2 所示的正值（P）、 零（Z）和负值（N）。
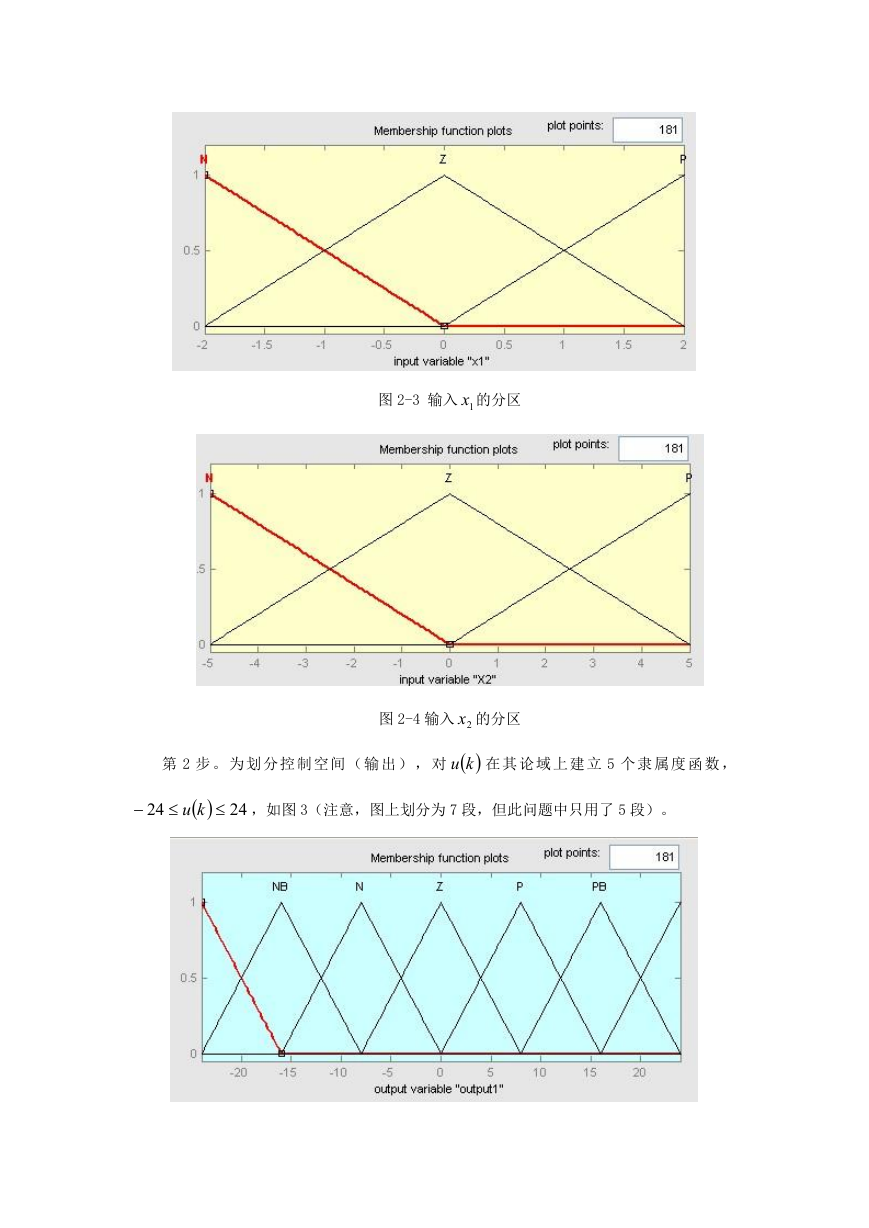
    图 2-3 输入 1x 的分区 图 2-4 输入 2x 的分区 第 2 步 。 为 划 分 控 制 空 间 （ 输 出 ） ， 对  ku 在 其 论 域 上 建 立 5 个 隶 属 度 函 数 ，  24    24 ku  ，如图 3（注意，图上划分为 7 段，但此问题中只用了 5 段）。
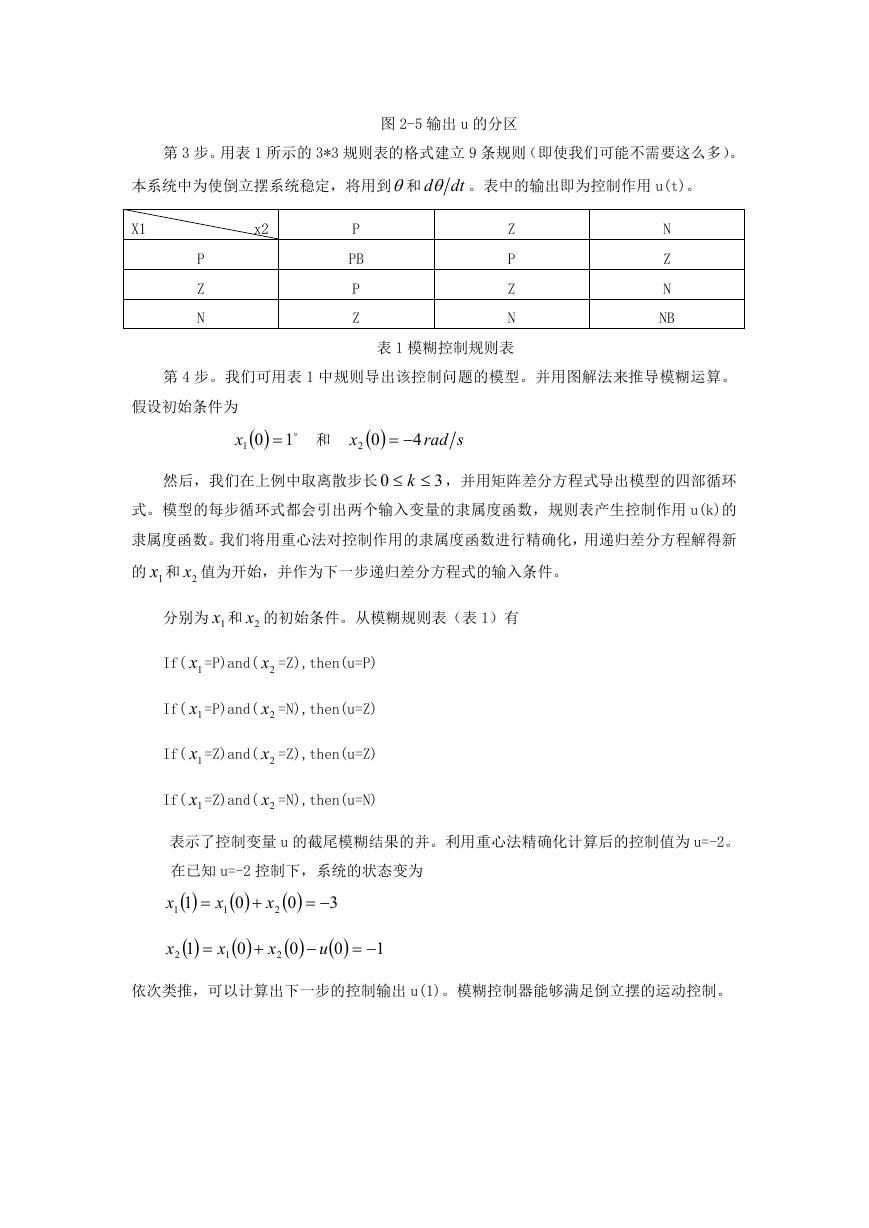
    图 2-5 输出 u 的分区 第 3 步。用表 1 所示的 3*3 规则表的格式建立 9 条规则（即使我们可能不需要这么多）。 本系统中为使倒立摆系统稳定，将用到和 dt d 。表中的输出即为控制作用 u(t)。 X1 x2 P Z N P PB P Z Z P Z N N Z N NB 第 4 步。我们可用表 1 中规则导出该控制问题的模型。并用图解法来推导模糊运算。 表 1 模糊控制规则表 假设初始条件为   01 x  1 和   02 x  4 rad s 然后，我们在上例中取离散步长  k ，并用矩阵差分方程式导出模型的四部循环 式。模型的每步循环式都会引出两个输入变量的隶属度函数，规则表产生控制作用 u(k)的 3 0 隶属度函数。我们将用重心法对控制作用的隶属度函数进行精确化，用递归差分方程解得新 的 1x 和 2x 值为开始，并作为下一步递归差分方程式的输入条件。 分别为 1x 和 2x 的初始条件。从模糊规则表（表 1）有 If( 1x =P)and( 2x =Z),then(u=P) If( 1x =P)and( 2x =N),then(u=Z) If( 1x =Z)and( 2x =Z),then(u=Z) If( 1x =Z)and( 2x =N),then(u=N) 表示了控制变量 u 的截尾模糊结果的并。利用重心法精确化计算后的控制值为 u=-2。 在已知 u=-2 控制下，系统的状态变为   1   0   0   3 x 2 x 1  x 1   1  x 2   0  x 1 x 2   0    0 u  1 依次类推，可以计算出下一步的控制输出 u(1)。模糊控制器能够满足倒立摆的运动控制。
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料