Robot Motion Planning and Control 4.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：1.11M 资料格式：pdf 举报版权申诉

weixin_38744375-11857041-16359647584877211423.pdf-第1页.png

第1页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第2页.png

第2页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第3页.png

第3页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第4页.png

第4页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第5页.png

第5页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第6页.png

第6页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第7页.png

第7页 / 共84页

weixin_38744375-11857041-16359647584877211423.pdf-第8页.png

第8页 / 共84页

Foreword

Table of contents

Introduction

Problem classification

Control issues

Open-loop vs. closed-loop control

Organization of contents

Modeling and analysis of the car-like robot

Kinematic modeling

Controllability analysis

Chained forms

Trajectory tracking

Reference trajectory generation

Control via approximate linearization

Control via exact feedback linearization

Path following and point stabilization

Control via smooth time-varying feedback

Control via nonsmooth time-varying feedback

About exponential convergence

Conclusions

Further reading

Feedback Control of a Nonholonomic Car-like Robot A. De Luca G. Oriolo C. Samson This is the fourth chapter of the book: Robot Motion Planning and Control Jean-Paul Laumond (Editor) Laboratoire d’Analye et d’Architecture des Syst`emes Centre National de la Recherche Scientiﬁque LAAS report 97438 Previoulsy published as: Lectures Notes in Control and Information Sciences 229. Springer, ISBN 3-540-76219-1, 1998, 343p.

Feedback Control of a Nonholonomic Car-Like Robot A. De Luca1, G. Oriolo1 and C. Samson2 1 Universit`a di Roma “La Sapienza” 2 INRIA, Sophia-Antipolis 1 Introduction The subject of this chapter is the control problem for nonholonomic wheeled mobile robots moving on the plane, and in particular the use of feedback tech- niques for achieving a given motion task. In automatic control, feedback improves system performance by allowing the successful completion of a task even in the presence of external disturbances and/or initial errors. To this end, real-time sensor measurements are used to reconstruct the robot state. Throughout this study, the latter is assumed to be available at every instant, as provided by proprioceptive (e.g., odometry) or exteroceptive (sonar, laser) sensors. We will limit our analysis to the case of a robot workspace free of obstacles. In fact, we implicitly consider the robot controller to be embedded in a hierar- chical architecture in which a higher-level planner solves the obstacle avoidance problem and provides a series of motion goals to the lower control layer. In this perspective, the controller deals with the basic issue of converting ideal plans into actual motion execution. Wherever appropriate, we shall highlight the in- teractions between feedback control and motion planning primitives, such as the generation of open-loop commands and the availability of a feasible smooth path joining the current robot position to the destination. The speciﬁc robotic system considered is a vehicle whose kinematic model approximates the mobility of a car. The conﬁguration of this robot is repre- sented by the position and orientation of its main body in the plane, and by the angle of the steering wheels. Two velocity inputs are available for motion control. This situation covers in a realistic way many of the existing robotic vehicles. Moreover, the car-like robot is the simplest nonholonomic vehicle that displays the general characteristics and the diﬃcult maneuverability of higher- dimensional systems, e.g., of a car towing trailers. As a matter of fact, the control results presented here can be directly extended to more general kine- matics, namely to all mobile robots admitting a chained-form representation. In particular, our choice encompasses the case of unicycle kinematics, another ubiquitous model of wheeled mobile robot, for which simple but speciﬁc feed- back control methods can also be derived.

172 A. De Luca, G. Oriolo and C. Samson The nonholonomic nature of the car-like robot is related to the assump- tion that the robot wheels roll without slipping. This implies the presence of a nonintegrable set of ﬁrst-order diﬀerential constraints on the conﬁguration variables. While these nonholonomic constraints reduce the instantaneous mo- tions that the robot can perform, they still allow global controllability in the conﬁguration space. This unique feature leads to some challenging problems in the synthesis of feedback controllers, which parallel the new research issues arising in nonholonomic motion planning. Indeed, the wheeled mobile robot application has triggered the search for innovative types of feedback controllers that can be used also for more general nonlinear systems. In the rest of this introduction, we present a classiﬁcation of motion control problems, discussing their intrinsic diﬃculty and pointing out the relationships between planning and control aspects. 1.1 Problem classiﬁcation In order to derive the most suitable feedback controllers for each case, it is convenient to classify the possible motion tasks as follows: – Point-to-point motion: The robot must reach a desired goal conﬁguration starting from a given initial conﬁguration. – Path following: The robot must reach and follow a geometric path in the cartesian space starting from a given initial conﬁguration (on or oﬀ the path). – Trajectory tracking: The robot must reach and follow a trajectory in the cartesian space (i.e., a geometric path with an associated timing law) start- ing from a given initial conﬁguration (on or oﬀ the trajectory). 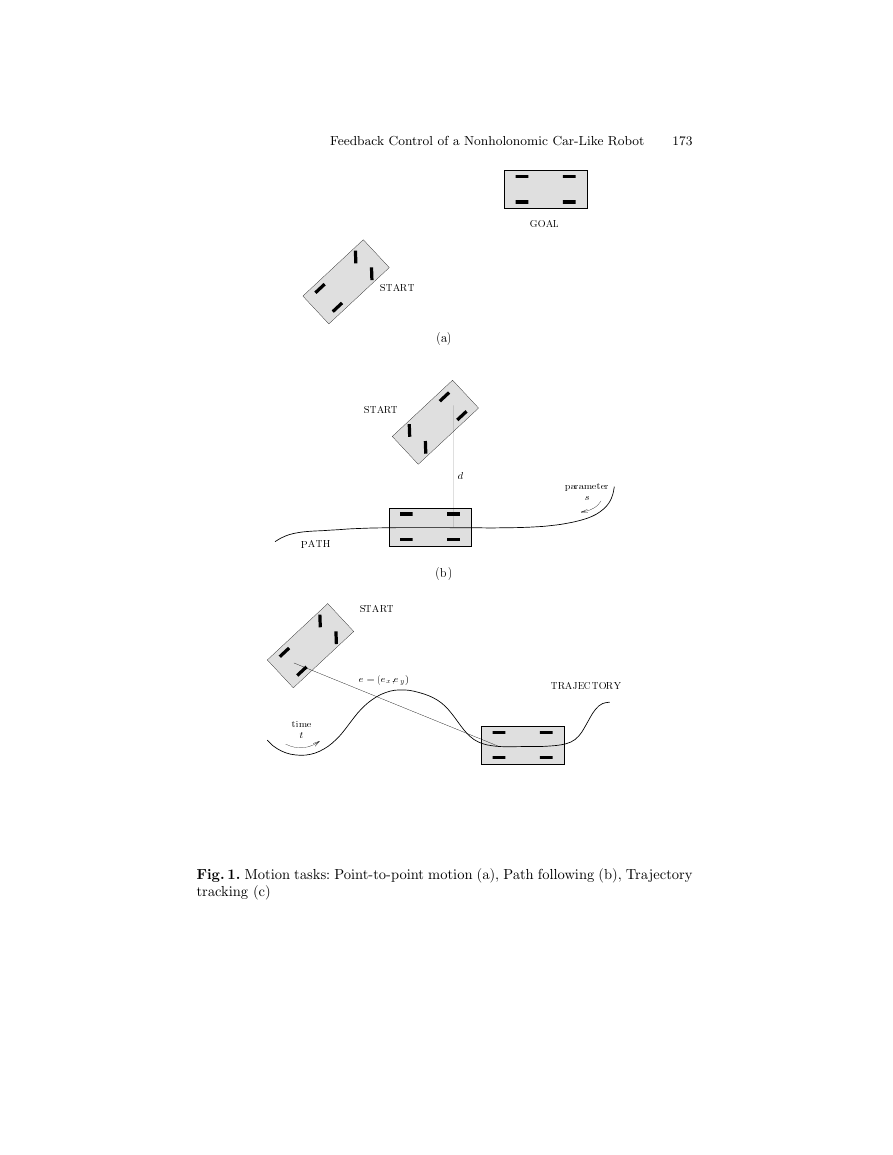The three tasks are sketched in Fig. 1, with reference to a car-like robot. Using a more control-oriented terminology, the point-to-point motion task is a stabilization problem for an (equilibrium) point in the robot state space. For a car-like robot, two control inputs are available for adjusting four conﬁguration variables, namely the two cartesian coordinates characterizing the position of a reference point on the vehicle, its orientation, and the steering wheels angle. More in general, for a car-like robot towing N trailers, we have two inputs for reconﬁguring n = 4 + N states. The error signal used in the feedback controller is the diﬀerence between the current and the desired conﬁguration.

Feedback Control of a Nonholonomic Car-Like Robot 173 Fig. 1. Motion tasks: Point-to-point motion (a), Path following (b), Trajectory tracking (c) !"#$%#$&('*)# ,+-./0#12435176.1789:

174 A. De Luca, G. Oriolo and C. Samson In the path following task, the controller is given a geometric description of the assigned cartesian path. This information is usually available in a param- eterized form expressing the desired motion in terms of a path parameter σ, which may be in particular the arc length along the path. For this task, time dependence is not relevant because one is concerned only with the geometric displacement between the robot and the path. In this context, the time evolu- tion of the path parameter is usually free and, accordingly, the command inputs can be arbitrarily scaled with respect to time without changing the resulting robot path. It is then customary to set the robot forward velocity (one of the two inputs) to an arbitrary constant or time-varying value, leaving the second input available for control. The path following problem is thus rephrased as the stabilization to zero of a suitable scalar path error function (the distance d to the path in Fig. 1b) using only one control input. For the car-like robot, we shall see that achieving d ≡ 0 implies the control of three conﬁguration variables— one less than the dimension of the conﬁguration space—because higher-order derivatives of the controlled output d are related to these variables. Similarly, in the presence of N trailers, requiring d ≡ 0 involves the control of as many as n − 1 = N + 3 coordinates using one input. In the trajectory tracking task, the robot must follow the desired carte- sian path with a speciﬁed timing law (equivalently, it must track a moving reference robot). Although the trajectory can be split into a parameterized ge- ometric path and a timing law for the parameter, such separation is not strictly necessary. Often, it is simpler to specify the workspace trajectory as the de- sired time evolution for the position of some representative point of the robot. The trajectory tracking problem consists then in the stabilization to zero of the two-dimensional cartesian error e (see Fig. 1c) using both control inputs. For the car-like robot, imposing e ≡ 0 over time implies the control of all four conﬁguration variables. Similarly, in the presence of N trailers, we are actually controlling n = N + 4 coordinates using two inputs. The point stabilization problem can be formulated in a local or in a global sense, the latter meaning that we allow for initial conﬁgurations that are arbi- trarily far from the destination. The same is true also for path following and trajectory tracking, although locality has two diﬀerent meanings in these tasks. For path following, a local solution means that the controller works properly provided we start suﬃciently close to the path; for trajectory tracking, close- ness should be evaluated with respect to the current position of the reference robot. The amount of information that should be provided by a high-level motion planner varies for each control task. In point-to-point motion, information is reduced to a minimum (i.e., the goal conﬁguration only) when a globally sta- bilizing feedback control solution is available. However, if the initial error is large, such a control may produce erratic behavior and/or large control eﬀort

Feedback Control of a Nonholonomic Car-Like Robot 175 which are unacceptable in practice. On the other hand, a local feedback solu- tion requires the deﬁnition of intermediate subgoals at the task planning level in order to get closer to the ﬁnal desired conﬁguration. For the other two motion tasks, the planner should provide a path which is kinematically feasible (namely, which complies with the nonholonomic con- straints of the speciﬁc vehicle), so as to allow its perfect execution in nominal conditions. While for an omnidirectional robot any path is feasible, some degree of geometric smoothness is in general required for nonholonomic robots. Nev- ertheless, the intrinsic feedback structure of the driving commands enables to recover transient errors due to isolated path discontinuities. Note also that the unfeasibility arising from a lack of continuity in some higher-order derivative of the path may be overcome by appropriate motion timing. For example, paths with discontinuous curvature (like the Reeds and Shepp optimal paths under maximum curvature constraint) can be executed by the real axle midpoint of a car-like vehicle provided that the robot is allowed to stop, whereas paths with discontinuous tangent are not feasible. In this analysis, the selection of the robot representative point for path/trajectory planning is critical. The timing proﬁle is the additional item needed in trajectory tracking con- trol tasks. This information is seldom provided by current motion planners, also because the actual dynamics of the speciﬁc robot are typically neglected at this level. The above example suggests that it may be reasonable to enforce already at the planning stage requirements such as ‘move slower where the path curvature is higher’. 1.2 Control issues From a control point of view, the previously described motion tasks are deﬁned for the nonlinear system ˙q = G(q)v, (1) representing the kinematic model of the robot. Here, q is the n-vector of robot generalized coordinates, v is the m-vector of input velocities (m < n), and the columns gi (i = 1, . . . , m) of matrix G are smooth vector ﬁelds. For the car-like robot, it is n = 4 and m = 2. The above model can be directly derived from the nonintegrable rolling constraints governing the system kinematic behavior. System (1) is driftless, a characteristic of ﬁrst-order kinematic models. Besides, its nonlinear nature is intrinsically related to the nonholonomy of the original Pfaﬃan constraints. In turn, it can be shown that this is equivalent to the global accessibility of the n-dimensional robot conﬁguration space—in spite of the reduced number of inputs.

176 A. De Luca, G. Oriolo and C. Samson Interestingly, the nonholonomy of system (1) reverses the usual order of dif- ﬁculty of robot control tasks. For articulated manipulators, and in general for all mechanical systems with as many control inputs as generalized coordinates, stabilization to a ﬁxed conﬁguration is simpler than tracking a trajectory. In- stead, stabilizing a wheeled mobile robot to a point is more diﬃcult than path following or trajectory tracking. A simple way to appreciate such a diﬀerence follows from the general discus- sion of the previous section. The point-to-point task is actually an input-state problem with m = 2 inputs and n controlled states. The path following task is an input-output problem with m = 1 input and p = 1 controlled output, implying the indirect control of n − 1 states. The trajectory tracking task is again an input-output problem with m = 2 inputs and p = 2 controlled out- puts, implying the indirect control of n states. As a result, the point-to-point motion task gives rise to the most diﬃcult control problem, since we are try- ing to control n independent variables using only two input commands. The path following and trajectory tracking tasks have a similar level of diﬃculty, being ‘square’ control problems (same number of control inputs and controlled variables). This conclusion can be supported by a more rigorous controllability analysis. In particular, one can test whether the above problems admit an approximate solution in terms of linear control design techniques. We shall see that if the system (1) is linearized at a ﬁxed conﬁguration, the resulting linear system is not controllable. On the other hand, the linearization of eq. (1) about a smooth trajectory gives rise to a linear time-varying system that is controllable, provided some persistency conditions are satisﬁed by the reference trajectory. The search for a feedback solution to the point stabilization problem is further complicated by a general theoretical obstruction. Although the kine- matic model (1) can be shown to be controllable using nonlinear tools from diﬀerential geometry, it fails to satisfy a necessary condition for stabilizabil- ity via smooth time-invariant feedback (Brockett’s theorem). This means that the class of stabilizing controllers should be suitably enlarged so as to include nonsmooth and/or time-varying feedback control laws. We ﬁnally point out that the design of feedback controllers for the path following task can be tackled from two opposite directions. In fact, by separat- ing the geometric and timing information of a trajectory, path following may be seen as a subproblem of trajectory tracking. On the other hand, looking at the problem from the point of view of controlled states (in the proper coordi- nates), path following appears as part of a point stabilization task. The latter philosophy will be adopted in this chapter.

Feedback Control of a Nonholonomic Car-Like Robot 177 1.3 Open-loop vs. closed-loop control Some comments are now appropriate concerning the relationships between the planning and control phases in robot motion execution. Essentially, we regard planning and open-loop (or feedforward) control as synonyms, as opposed to feedback control. In a general setting, a closed-loop controller results from the superposition of a feedback action to a coherent feedforward term. The latter is determined based on a priori knowledge about the motion task and the environment, which may have been previously acquired by exteroceptive sensors. Feedback control is instead computed in real-time based on external/internal sensor data. However, the borderline between open-loop and closed-loop control solu- tions may not be so sharp. In fact, we may use repeated open-loop phases, replanned at higher rates using new sensor data to gather information on the actual state. In the limit, continuous sensing and replanning leads to a feedback solution. Although this scheme is conceptually simple, its convergence analysis may not be easy. Thus, we prefer to consider the planning and control phases separately. For wheeled mobile robots, the usual output of the planning phase, which takes into account the obstacle avoidance requirement, is a kinematically fea- sible path with associated nominal open-loop commands. To guarantee fea- sibility, the planner may either take directly into account the nonholonomic constraints in the generation of a path, or create a preliminary holonomic path with standard techniques and then approximate it with a concatenation of feasible subpaths. In the planning phase, it is also possible to include an optimality criterion together with system state and input constraints. It is often possible to obtain a solution by applying optimal (open-loop) control results. A typical cost cri- terion for the car-like robot is the total length of the collision-free path joining source to destination, while constraints include bounds on the steering angle as well as on the linear and angular velocity. In any case, the resulting com- mands are computed oﬀ-line. Hence, unmodeled events at running time, such as occasional slipping of the wheels or erroneous initial localization, will prevent the successful completion of a point-to-point motion or the correct tracing of a desired path. The well-known answer to such problems is resorting to a feedback con- troller, driven by the current task error, so as to achieve some degree of ro- bustness. However, this should by no means imply the abdication to the use of the nominal open-loop command computed in the planning phase, which is included as the feedforward term in the closed-loop controller. As soon as the task error is zero, the feedback signal is not in action and the output command of the controller coincides with the feedforward term.

分享到：

赞收藏

资料库

Robot Motion Planning and Control 4.pdf

相关推荐

开发技术

热门标签

最新资料