logo资料库

实验一平行束投影数据采集与滤波反投影重建实验.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.16M 资料格式：doc 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    实验报告 实验一、平行束投影数据采集与滤波反投影重建实验 一、实验目的及要求： 用程序模拟 X 射线的投影，获得 Shepp-Logan 模型的投影数据。对获得的投影数据进 行滤波反投影重建，获得 Shepp-Logan 模型的重建图像。 二、实验基本原理： X 射线穿过人体时，人体的各种组织对 X 射线有不同程度的衰减，即不同的组织有不 同的线性衰减系数μ。假设强度为 I0 的 X 射线穿过均匀分布衰减系数为μ的物体，行进了 x 的距离，强度变为 I，按 Beer 定理有 或 ① 若物体时分段均匀的，系数分别是μ1、μ2、μ3、...,相应的长度为 x1，x2，x3，...,则下式成 立： ② 更一般的可用下面的积分式表示： ③ 由 于 只 是 模 拟 X 射 线 的 投 影 过 程 ， 我 们 简 化 了 问 题 。 假 设 断 面 的 结 构 如 图 1.1 （Shepp-Logan）所示（各图元均为椭圆），各个椭圆表示了人体的不同的组织（内部是均匀 的），分别有不同的线性衰减系数μ。那么，就可利用公式②来求某条 X 射线投影值。各个 椭圆（组织）的线性衰减系数μ（Shepp-Logan 图的各椭圆的位置、大小和线性衰减系数参 见表 1.1）是已知的，问题就是球 X 射线穿过椭圆时的行进距离。设椭圆的长短轴为 a，b； X 射线与 b 的夹角为Φ；椭圆中心到 X 射线的距离为 d。如图 1.2 所示。这样可由④⑤求得 X 射线穿过椭圆时的行进距离。再乘上各个椭圆的线性衰减系数μ后累加起来就可得到 X 射 线的投影值。 ④ ⑤
    图 1.1 图 1.2 表 1.1Shepp-Logan 头部模型 参数编号 cx(中心 x 座标) 1 2 3 4 5 6 7 8 9 10 11 0.5538 0.06 0 -0.08 0 0 0 -0.22 0.22 0 0 yx(中心 y 座标) -0.3858 -0.605 -0.605 -0.605 -0.1 0.1 0.35 0 0 -0.0184 0 a(水平轴) 0.033 0.023 0.023 0.046 0.046 0.046 0.21 0.16 0.11 0.6624 0.69 b(垂直轴) 0.206 0.023 0.023 0.023 0.046 0.046 0.25 0.41 0.31 0.874 0.92 r(椭圆倾角) μ(线性衰减系数) -18 0 0 0 0 0 0 18 -18 0 0 0.03 0.01 0.01 0.01 0.01 0.01 0.01 -0.02 -0.02 -0.98 1 表 1.1 r 的单位是角度，μ为负值时表示削弱原有椭圆的衰减系数 利用滤波反投影重建算法，实现对 Shep-Logan 头模型的重建。要用到的原理有：傅立 叶切片定理、快速傅立叶变换 FFT 以及滤波函数的设计。 三、主要仪器设备及实验耗材： 具有 XP 或 2000 系统，并装有 MATLAB 系统的 PC 机。 四、实验内容及结果： 1．用 MATLAB 图像处理工具箱的 phantom 生成 Shep-Logan 头模型； P=phantom(256); imshow(P)
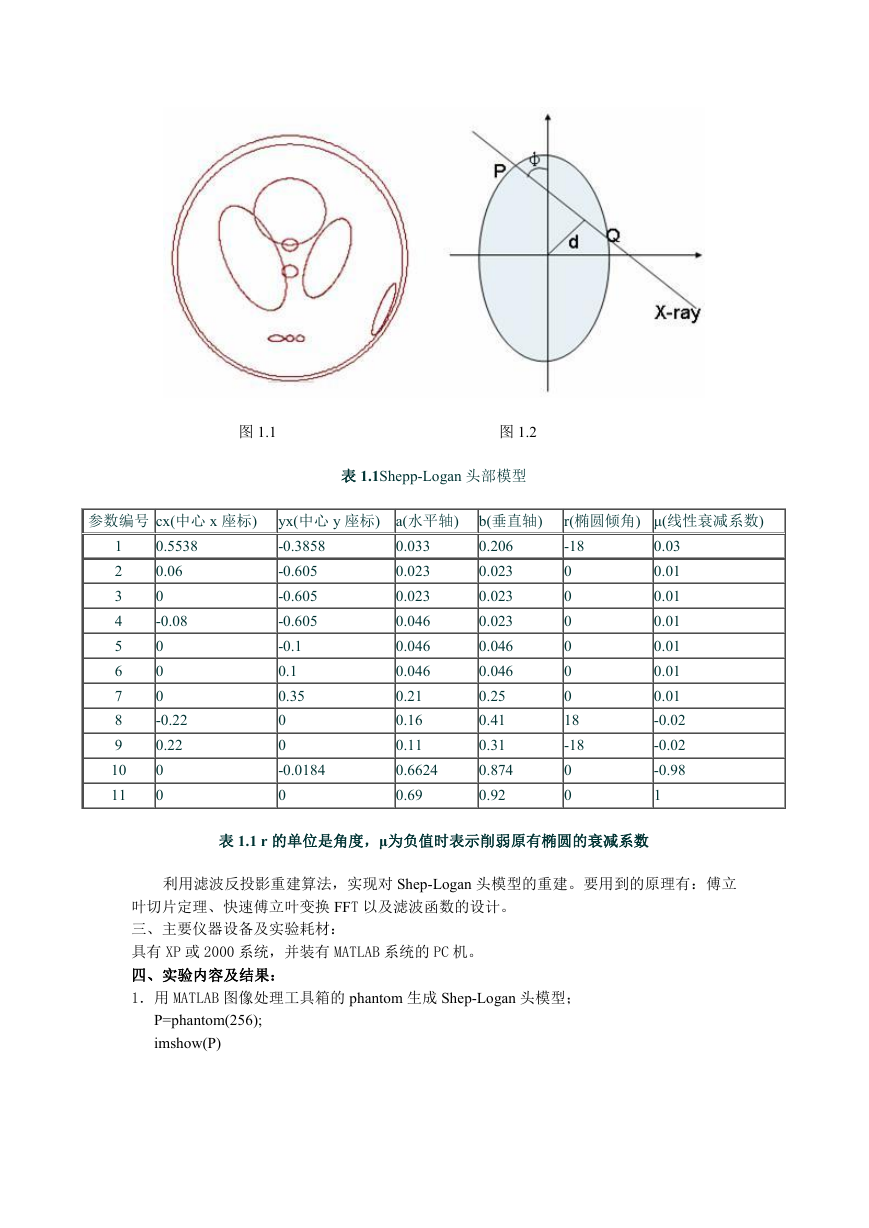
    2．用 MATLAB 中的 radon 函数获得 Shepp-Logan 模型的投影数据； 计算 Shep-Logen 头模型 18 个角度、36 个角度、90 个角度和 180 个角度的投影数据。 theta1=0:10:170;[R1,xp]=radon(P,theta1); theta2=0:5:175;[R2,xp]=radon(P,theta2); theta3=0:2:178;[R3,xp]=radon(P,theta3); theta4=0:1:179;[R3,xp]=radon(P,theta4); 显示投影数据： figure,imagesc（theta1,xp,R1）;xlabel（’\theta’）;ylabel（’x\prime’）; figure,imagesc（theta2,xp,R2）;xlabel（’\theta’）;ylabel（’x\prime’）; figure,imagesc（theta3,xp,R3）;xlabel（’\theta’）;ylabel（’x\prime’）; figure,imagesc（theta4,xp,R4）;xlabel（’\theta’）;ylabel（’x\prime’）;
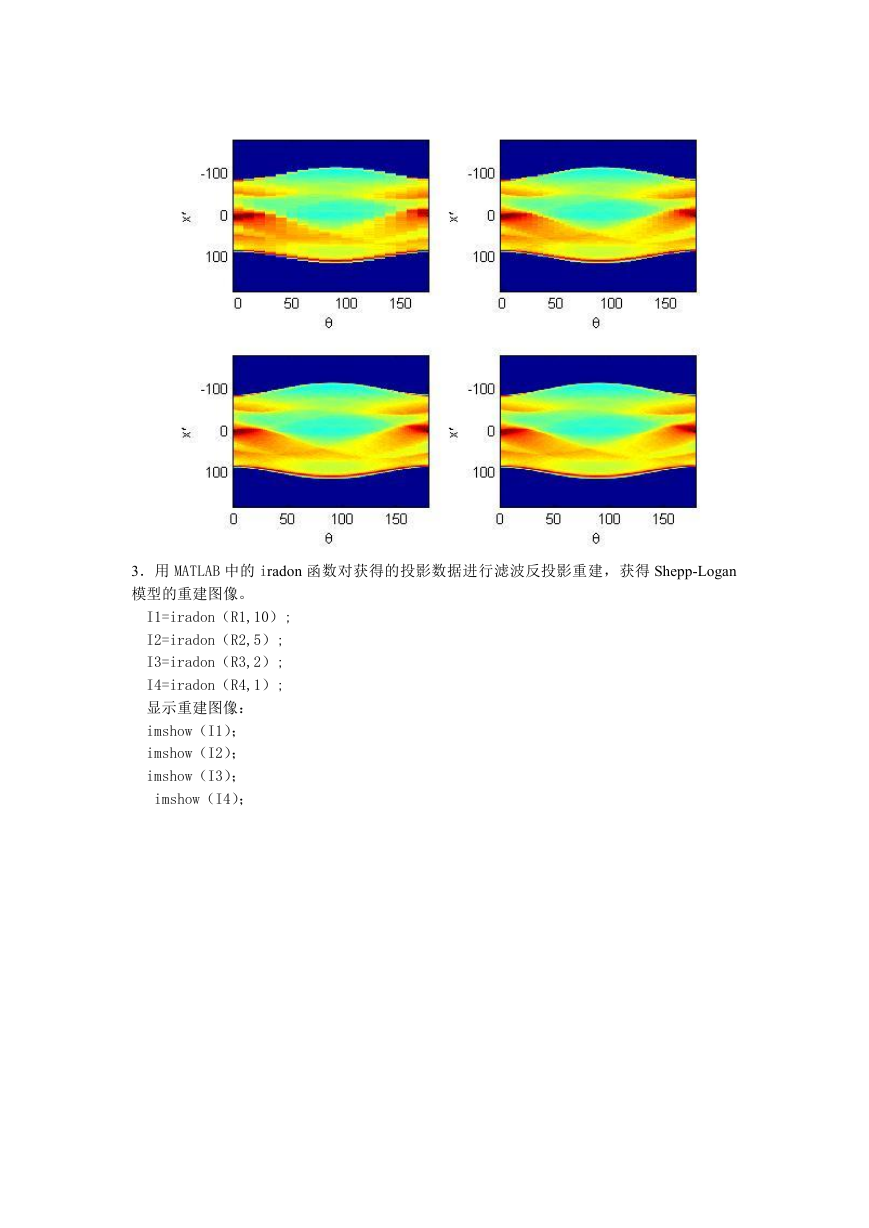
    3．用 MATLAB 中的 iradon 函数对获得的投影数据进行滤波反投影重建，获得 Shepp-Logan 模型的重建图像。 I1=iradon（R1,10）; I2=iradon（R2,5）; I3=iradon（R3,2）; I4=iradon（R4,1）; 显示重建图像： imshow（I1）； imshow（I2）； imshow（I3）； imshow（I4）；
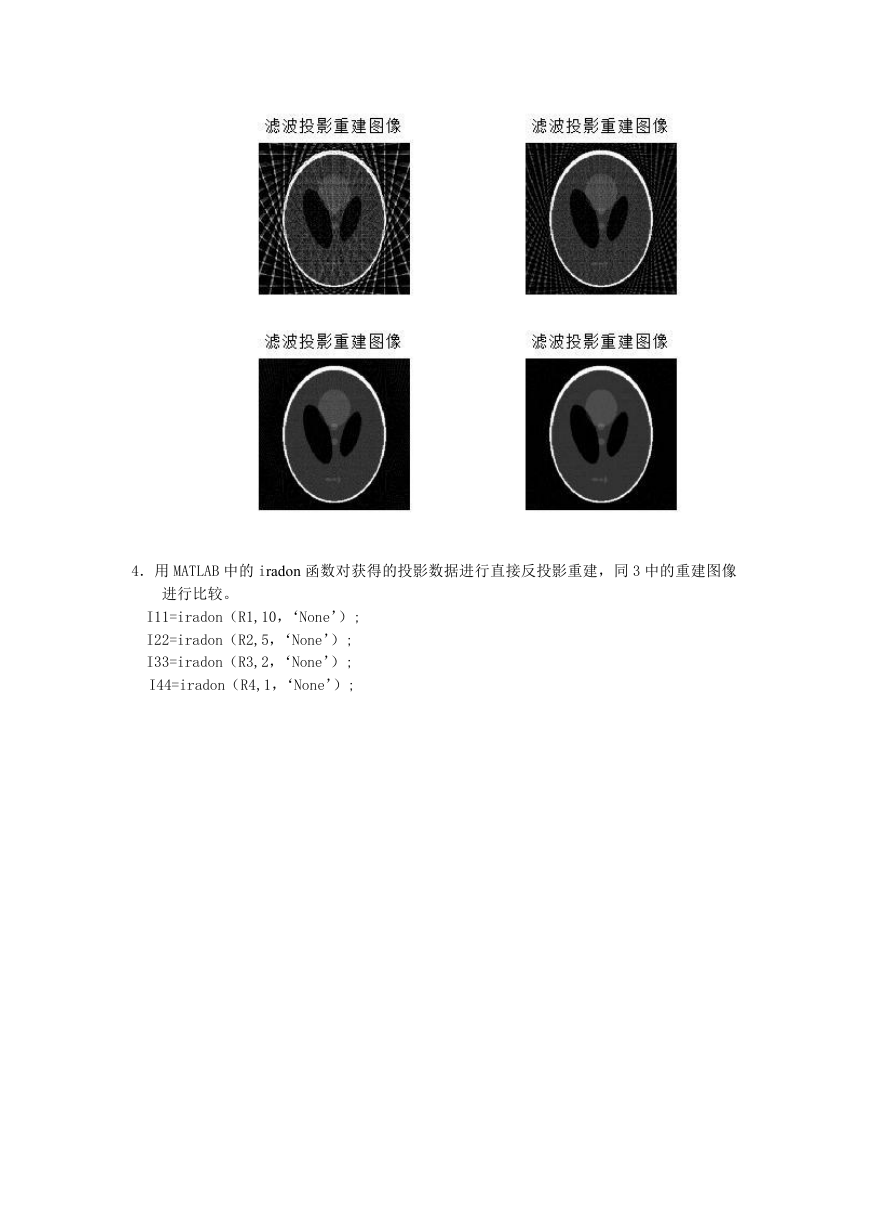
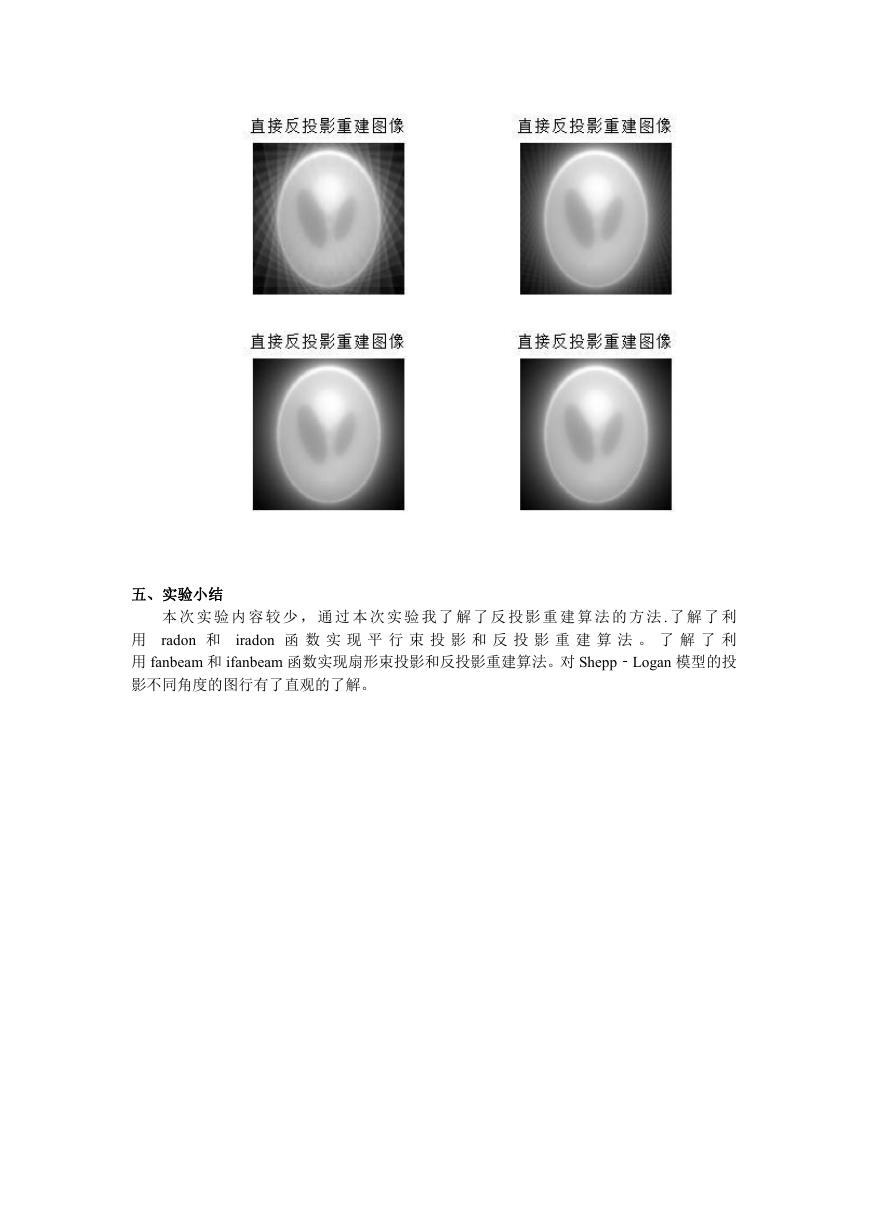
    4．用 MATLAB 中的 iradon 函数对获得的投影数据进行直接反投影重建，同 3 中的重建图像 进行比较。 I11=iradon（R1,10，‘None’）; I22=iradon（R2,5，‘None’）; I33=iradon（R3,2，‘None’）; I44=iradon（R4,1，‘None’）;
    五、实验小结 本 次 实 验 内 容 较 少 ， 通 过 本 次 实 验 我 了 解 了 反 投 影 重 建 算 法 的 方 法 . 了 解 了 利 用 radon 和 iradon 函 数 实 现 平 行 束 投 影 和 反 投 影 重 建 算 法 。 了 解 了 利 用 fanbeam 和 ifanbeam 函数实现扇形束投影和反投影重建算法。对 Shepp‐Logan 模型的投 影不同角度的图行有了直观的了解。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料