2021年江苏省连云港市中考数学真题及答案.doc

发布时间：2022-08-24 发布人：admin 分类：说明书资料大小：0.95M 资料格式：doc 举报版权申诉

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

文本预览

2021 年江苏省连云港市中考数学真题及答案一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上） 1．﹣3 的相反数是（） A．3 B． C．﹣3 D．﹣ 2．下列运算正确的是（） A．3a+2b＝5ab C．7a+a＝7a2 B．5a2﹣2b2＝3 D．（x﹣1）2＝x2+1﹣2x 3．2021 年 5 月 18 日上午，江苏省人民政府召开新闻发布会，公布了全省最新人口数据，其中连云港市的常住人口约为 4600000 人．把“4600000”用科学记数法表示为（） A．0.46×107 B．4.6×107 C．4.6×106 D．46×105 4．正五边形的内角和是（） A．360° B．540° C．720° D．900° 5．如图，将矩形纸片 ABCD沿 EF折叠后，点 D、C分别落在点 D1、C1 的位置，ED1 的延长线交 BC于点 G，若∠EFG＝64°，则∠EGB等于（） A．128° B．130° C．132° D．136° 6．关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．甲：函数图像经过点（﹣1，1）；乙：函数图像经过第四象限；丙：当 x＞0 时，y随 x的增大而增大．则这个函数表达式可能是（）

A．y＝﹣x B．y＝ C．y＝x2 D．y＝﹣ 7．如图，△ABC中，BD⊥AB，BD、AC相交于点 D，AD＝ AC，AB＝2，∠ABC＝150°，则△ DBC的面积是（） A． B． C． D． 8．如图，正方形 ABCD内接于⊙O，线段 MN在对角线 BD上运动，若⊙O的面积为 2π，MN ＝1，则△AMN周长的最小值是（） A．3 B．4 C．5 D．6 二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分.不需要写出解答过程，请把答案直接填写在答题卡相应位置上） 9．一组数据 2，1，3，1，2，4 的中位数是． 10．计算：＝． 11．分解因式：9x2+6x+1＝． 12．若关于 x的方程 x2﹣3x+k＝0 有两个相等的实数根，则 k＝． 13．如图，OA、OB是⊙O的半径，点 C在⊙O上，∠AOB＝30°，∠OBC＝40°，则∠OAC＝ °．

14．如图，菱形 ABCD的对角线 AC、BD相交于点 O，OE⊥AD，垂足为 E，AC＝8，BD＝6，则 OE的长为． 15．某快餐店销售 A、B两种快餐，每份利润分别为 12 元、8 元，每天卖出份数分别为 40 份、80 份．该店为了增加利润，准备降低每份 A种快餐的利润，同时提高每份 B种快餐的利润．售卖时发现，在一定范围内，每份 A种快餐利润每降 1 元可多卖 2 份，每份 B 种快餐利润每提高 1 元就少卖 2 份．如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是元． 16．如图，BE是△ABC的中线，点 F在 BE上，延长 AF交 BC于点 D．若 BF＝3FE，则＝．三、解答题（本大题共 11 小题，共 102 分.请在答题卡指定区域内作答，解答时写出必要的文字说明、证明过程或演算步骤） 17．计算： +|﹣6|﹣22． 18．解不等式组：．

19．解方程： ﹣ ＝1． 20．端午节吃粽子是中华民族的传统习俗．某食品厂为了解市民对去年销量较好的 A、B、C、 D四种粽子的喜爱情况，在端午节前对某小区居民进行抽样调查（每人只选一种粽子），并将调查情况绘制成如下两幅尚不完整的统计图．根据以上信息，解答下列问题：（1）补全条形统计图；（2）扇形统计图中，D种粽子所在扇形的圆心角是 °；（3）这个小区有 2500 人，请你估计爱吃 B种粽子的人数为． 21．为了参加全市中学生“党史知识竞赛”，某校准备从甲、乙 2 名女生和丙、丁 2 名男生中任选 2 人代表学校参加比赛．（1）如果已经确定女生甲参加，再从其余的候选人中随机选取 1 人，则女生乙被选中的概率是；（2）求所选代表恰好为 1 名女生和 1 名男生的概率． 22．如图，点 C是 BE的中点，四边形 ABCD是平行四边形．（1）求证：四边形 ACED是平行四边形；（2）如果 AB＝AE，求证：四边形 ACED是矩形． 23．为了做好防疫工作，学校准备购进一批消毒液．已知 2 瓶 A型消毒液和 3 瓶 B型消毒液

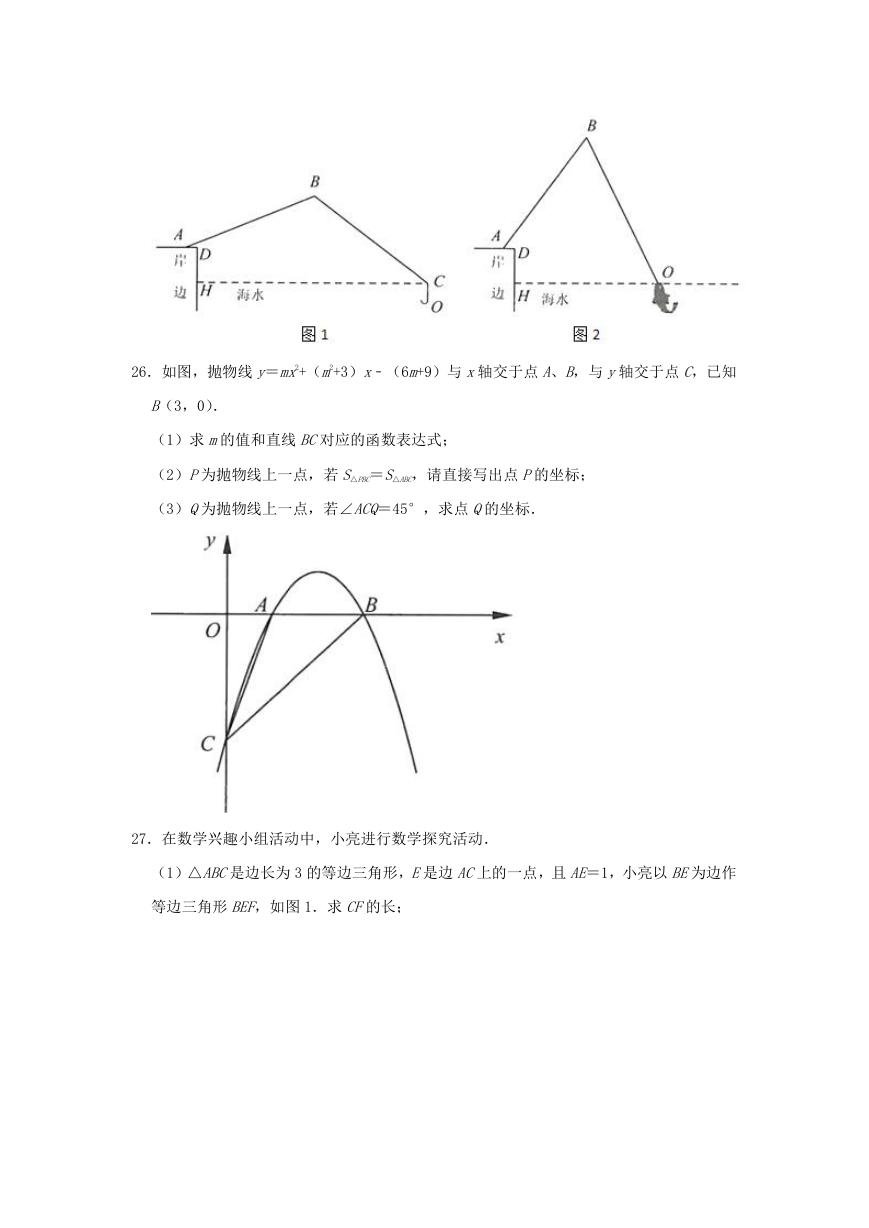
共需 41 元，5 瓶 A型消毒液和 2 瓶 B型消毒液共需 53 元．（1）这两种消毒液的单价各是多少元？（2）学校准备购进这两种消毒液共 90 瓶，且 B型消毒液的数量不少于 A型消毒液数量的，请设计出最省钱的购买方案，并求出最少费用． 24．如图，Rt△ABC中，∠ABC＝90°，以点 C为圆心，CB为半径作⊙C，D为⊙C上一点，连接 AD、CD，AB＝AD，AC平分∠BAD．（1）求证：AD是⊙C的切线；（2）延长 AD、BC相交于点 E，若 S△EDC＝2S△ABC，求 tan∠BAC的值． 25．我市的前三岛是众多海钓人的梦想之地．小明的爸爸周末去前三岛钓鱼，将鱼竿 AB摆成如图 1 所示．已知 AB＝4.8m，鱼竿尾端 A离岸边 0.4m，即 AD＝0.4m．海面与地面 AD 平行且相距 1.2m，即 DH＝1.2m．（1）如图 1，在无鱼上钩时，海面上方的鱼线 BC与海面 HC的夹角∠BCH＝37°，海面下方的鱼线 CO与海面 HC垂直，鱼竿 AB与地面 AD的夹角∠BAD＝22°．求点 O到岸边 DH 的距离；（2）如图 2，在有鱼上钩时，鱼竿与地面的夹角∠BAD＝53°，此时鱼线被拉直，鱼线 BO＝5.46m，点 O恰好位于海面．求点 O到岸边 DH的距离．（参考数据：sin37°＝cos53°≈ ，cos37°＝sin53°≈ ，tan37°≈ ，sin22° ≈ ，cos22°≈ ，tan22°≈ ）

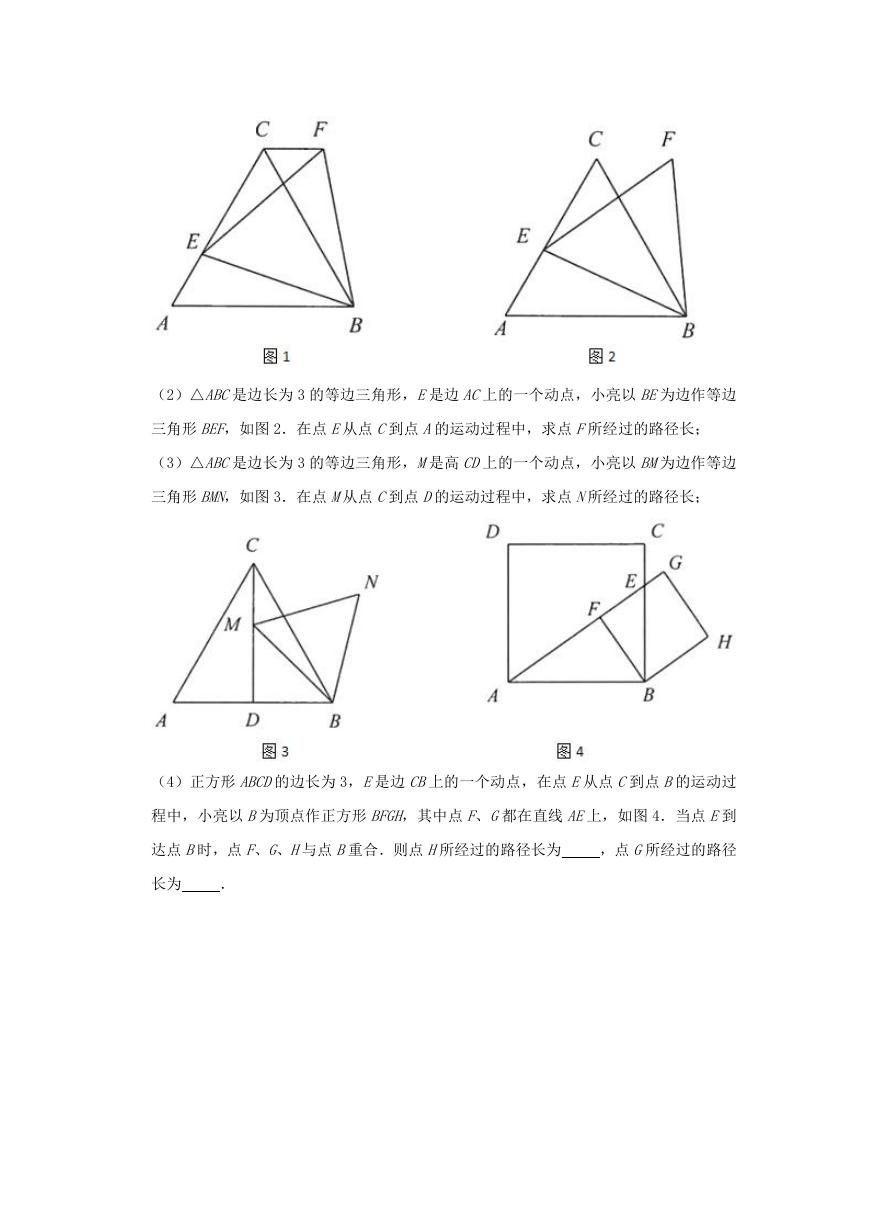
26．如图，抛物线 y＝mx2+（m2+3）x﹣（6m+9）与 x轴交于点 A、B，与 y轴交于点 C，已知 B（3，0）．（1）求 m的值和直线 BC对应的函数表达式；（2）P为抛物线上一点，若 S△PBC＝S△ABC，请直接写出点 P的坐标；（3）Q为抛物线上一点，若∠ACQ＝45°，求点 Q的坐标． 27．在数学兴趣小组活动中，小亮进行数学探究活动．（1）△ABC是边长为 3 的等边三角形，E是边 AC上的一点，且 AE＝1，小亮以 BE为边作等边三角形 BEF，如图 1．求 CF的长；

（2）△ABC是边长为 3 的等边三角形，E是边 AC上的一个动点，小亮以 BE为边作等边三角形 BEF，如图 2．在点 E从点 C到点 A的运动过程中，求点 F所经过的路径长；（3）△ABC是边长为 3 的等边三角形，M是高 CD上的一个动点，小亮以 BM为边作等边三角形 BMN，如图 3．在点 M从点 C到点 D的运动过程中，求点 N所经过的路径长；（4）正方形 ABCD的边长为 3，E是边 CB上的一个动点，在点 E从点 C到点 B的运动过程中，小亮以 B为顶点作正方形 BFGH，其中点 F、G都在直线 AE上，如图 4．当点 E到达点 B时，点 F、G、H与点 B重合．则点 H所经过的路径长为，点 G所经过的路径长为．

分享到：

赞收藏

资料库

2021年江苏省连云港市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料