ARIMA模型在江苏省GDP预测中的运用.pdf-资料库

weixin_38509656-12161368-4744302543412277872.pdf-第1页.png

第1页 / 共6页

weixin_38509656-12161368-4744302543412277872.pdf-第2页.png

第2页 / 共6页

weixin_38509656-12161368-4744302543412277872.pdf-第3页.png

第3页 / 共6页

weixin_38509656-12161368-4744302543412277872.pdf-第4页.png

第4页 / 共6页

weixin_38509656-12161368-4744302543412277872.pdf-第5页.png

第5页 / 共6页

weixin_38509656-12161368-4744302543412277872.pdf-第6页.png

第6页 / 共6页

中国科技论文在线 http://www.paper.edu.cn ARIMA模型在江苏省GDP预测中的运用赵伟东南大学经济管理学院南京 211189 Cmes1988@163.com 摘要：本文综合运用时间序列预浏方法，建立了1978一2008年江苏省GDP的时间序列单整自回归移动平均模型(ARIMA)。结果显示ARIMA(2,1,1)模型能能够提供较为准确的预测结果，并用以预测2009年江苏省生产总值，以此为江苏省经济发展提供参考数据。最后在本文的研究结果基础上提出几点政策建议。关键词：ARIMA模型 GDP预测时间序列国内生产总值(Gross Domestic Product，GDP)是一个国家或地区在一定时期内所生产和提供的最终货物和服务的总价值。国内生产总值是反映一个国家或地区的国民经济的生产规模及综合实力的总量指标，在经济研究中发挥着重要的作用。对GDP作正确的预测能为宏观经济健康发展起到导向性作用，并为高层政策决策者提供决策依据。在实际应用中，由于 GDP不仅受经济基础还受到人口增长、资源、科技等诸多因素的影响，而这些因素之间又有着错综复杂的关系，因此，对GDP的预测存在众多的不确定因素,尤其是突发因素对GDP预测的影响。如208年爆发的国际金融危机。移动平均自回归模型(ARIMA)是一类常用的随机时序模型。它是一种精度较高的时间序列短期预测方法。它主要试图解决以下两个问题：一是分析时间序列的随机性、平稳性和季节性；二是在对时间序列分析的基础上选择适当的模型进行预测。本文通过应用时间序列分析和预测的方法，建立了江苏省国内生产总值的ARIMA模型并进行了预测，取得了较好的效果。[1] 一、数据处理 1、GDP 数据自改革开放三十年来，江苏省GDP每年平均增长达12.6%。2006年江苏省国内生产总值突破2万亿元，达到21645.08亿元，2007江苏省GDP总值达到25741.15亿元。据统计数字显示江苏省2008年GDP超过3万亿元，同比增幅达到12.5%。改革开放后，尤其是自1990年以来，江苏省经济经历了长时间的高速发展。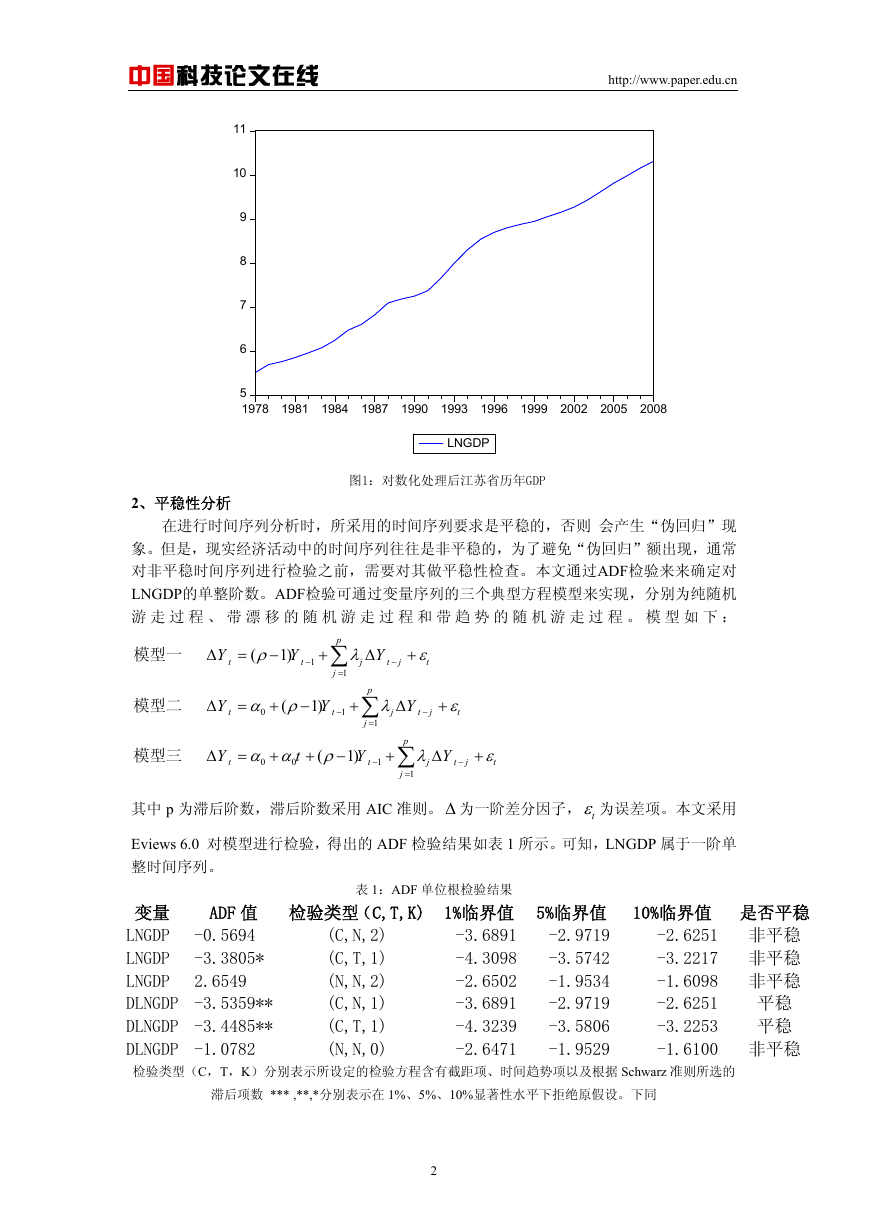为避免产生异方差现象，本文将江苏省1978—2008 年31年间的GDP数值进行对数化处理，即LNGDP=LOG(GDP)，DLNGDP与D(LOG(GDP)) 均为LNGDP的一阶差分。处理后的GDP如图1所示。可以看出，江苏省的GDP呈现出比较平稳的经济增长速度。数据分别来源于2008年《江苏省统计年鉴》和2008年江苏省国民经济和社会发展统计公报。 1

中国科技论文在线 http://www.paper.edu.cn 11 10 9 8 7 6 5 1978 1981 1984 1987 1990 1993 1996 1999 2002 2005 2008 LNGDP 图1：对数化处理后江苏省历年GDP 2、平稳性分析在进行时间序列分析时，所采用的时间序列要求是平稳的，否则会产生“伪回归”现象。但是，现实经济活动中的时间序列往往是非平稳的，为了避免“伪回归”额出现，通常对非平稳时间序列进行检验之前，需要对其做平稳性检查。本文通过ADF检验来来确定对 LNGDP的单整阶数。ADF检验可通过变量序列的三个典型方程模型来实现，分别为纯随机游走过程、带漂移的随机游走过程和带趋势的随机游走过程。模型如下： Y Δ 模型一 Y Δ 模型二 Y Δ 模型三 t t t = ( ρ − Y 1) + t 1 − p ∑ j 1 = λ j Y Δ t − j + ε t = = α ρ − + ( 0 Y 1) + t 1 − p ∑ j 1 = λ j Y Δ t − j + ε t α α ρ − + + ( t 0 0 Y 1) + t 1 − p ∑ j 1 = λ j Δ Y t − j + ε t 其中 p 为滞后阶数，滞后阶数采用 AIC 准则。 Δ 为一阶差分因子， tε 为误差项。本文采用 Eviews 6.0 对模型进行检验，得出的 ADF 检验结果如表 1 所示。可知，LNGDP 属于一阶单整时间序列。表 1：ADF 单位根检验结果 ADF 值检验类型（C,T,K) 1%临界值 5%临界值 10%临界值是否平稳变量 LNGDP -0.5694 LNGDP -3.3805* LNGDP 2.6549 DLNGDP -3.5359** DLNGDP -3.4485** DLNGDP -1.0782 检验类型（C，T，K）分别表示所设定的检验方程含有截距项、时间趋势项以及根据 Schwarz 准则所选的 (C,N,2) (C,T,1) (N,N,2) (C,N,1) (C,T,1) (N,N,0) -2.9719 -3.5742 -1.9534 -2.9719 -3.5806 -1.9529 -3.6891 -4.3098 -2.6502 -3.6891 -4.3239 -2.6471 -2.6251 非平稳 -3.2217 非平稳 -1.6098 非平稳 -2.6251 -3.2253 -1.6100 非平稳平稳平稳滞后项数 *** ,**,*分别表示在 1%、5%、10%显著性水平下拒绝原假设。下同 2

中国科技论文在线二、ARIMA建立模型 1、模型思想 http://www.paper.edu.cn 1970年Box-Jerkins提出了以随机理论为基础的时间序列分析方法，其基本模型包括三种：自回归(AR)模型；移动平均(MA)模型；单整自回归移动平均(ARIMA)模型，使模型同时综合考虑了预测变量的过去值、当前值和误差值，从而有效地提高了模型的预测精度。 ARIMA(p,d,q)模型又称为自回归移动平均模型。其中，AR指自回归，p为模型的自回归项数；MA为移动平均，q为模型的移动平均项数汪指积分，d为时间序列成为平稳之间必须取其差分的次数，即其单整阶数。[2] ARMA(p,q)模型的一般表达式如下。其中Yt为平稳时间序列，即Yt~I(0)。 Y ϕ ϕ t 2 μ θμ θμ θμ t q − ... + + Y p t p Y ϕ t 3 − − Y t 1 ϕ Y t + − − = + + 1 − 1 − − − − − q 2 3 1 2 2 t t t 若Yt为d阶单整的时间序列，即Yt~I(d)，则为ARIMA(p,d,q)模型。Yt经过下式变换后可转换为为零阶单整序列。 ω = d t Y t (1 = − L Y ) t ω ϕω ϕω ϕω t − = + + 1 − − 1 2 2 3 t t t ... + + 3 ϕω μ θμ θμ θμ t q − − − t p − + − − 1 − − p q 1 2 2 t t t 2、建立模型由表1的数据平稳性检验可知，LNGDP属于一阶单整，即差分后的LNGDP为平稳的时间序列。为确定ARIMA(p,d,q)模型中的p，q的阶数，对DLNGDP进行相关系数检验，结果如图2 所示。从图2可以看出，DLNGDP序列自相关系数在1阶出截尾，偏相关系数在2阶出截尾，即p=2，q=1。图2：DLNGDP相关系数建立利用ARIMA模型如下： D LOG GDP C )) = + ( ( ⋅ β 1 DLNGDP ( 1) − + β 2 ⋅ DLNGDP ( 2) − + μ β μ− t t 1 − ⋅ 3 3

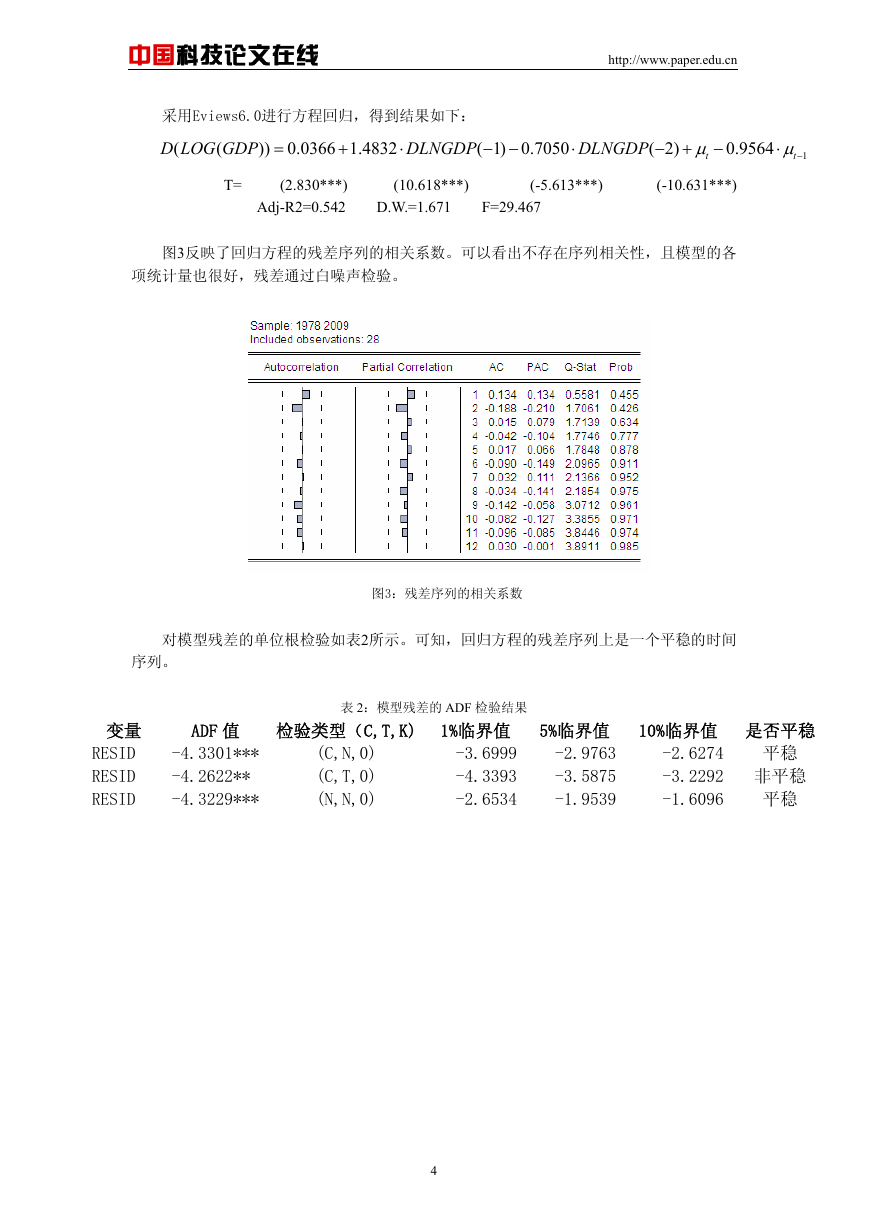
中国科技论文在线 http://www.paper.edu.cn 采用Eviews6.0进行方程回归，得到结果如下： DLNGDP D LOG GDP )) 0.0366 1.4832 = + ( ( ⋅ ( 1) 0.7050 − − ⋅ DLNGDP ( 2) − + μ t − 0.9564 ⋅ μ− t 1 T= (2.830***) (10.618***) (-5.613***) (-10.631***) Adj-R2=0.542 D.W.=1.671 F=29.467 图3反映了回归方程的残差序列的相关系数。可以看出不存在序列相关性，且模型的各项统计量也很好，残差通过白噪声检验。图3：残差序列的相关系数对模型残差的单位根检验如表2所示。可知，回归方程的残差序列上是一个平稳的时间序列。表 2：模型残差的 ADF 检验结果 ADF 值检验类型（C,T,K) -4.3301*** -4.2622** -4.3229*** (C,N,0) (C,T,0) (N,N,0) 1%临界值 -3.6999 -4.3393 -2.6534 5%临界值 -2.9763 -3.5875 -1.9539 10%临界值是否平稳 -2.6274 平稳 -3.2292 非平稳 -1.6096 平稳变量 RESID RESID RESID 4

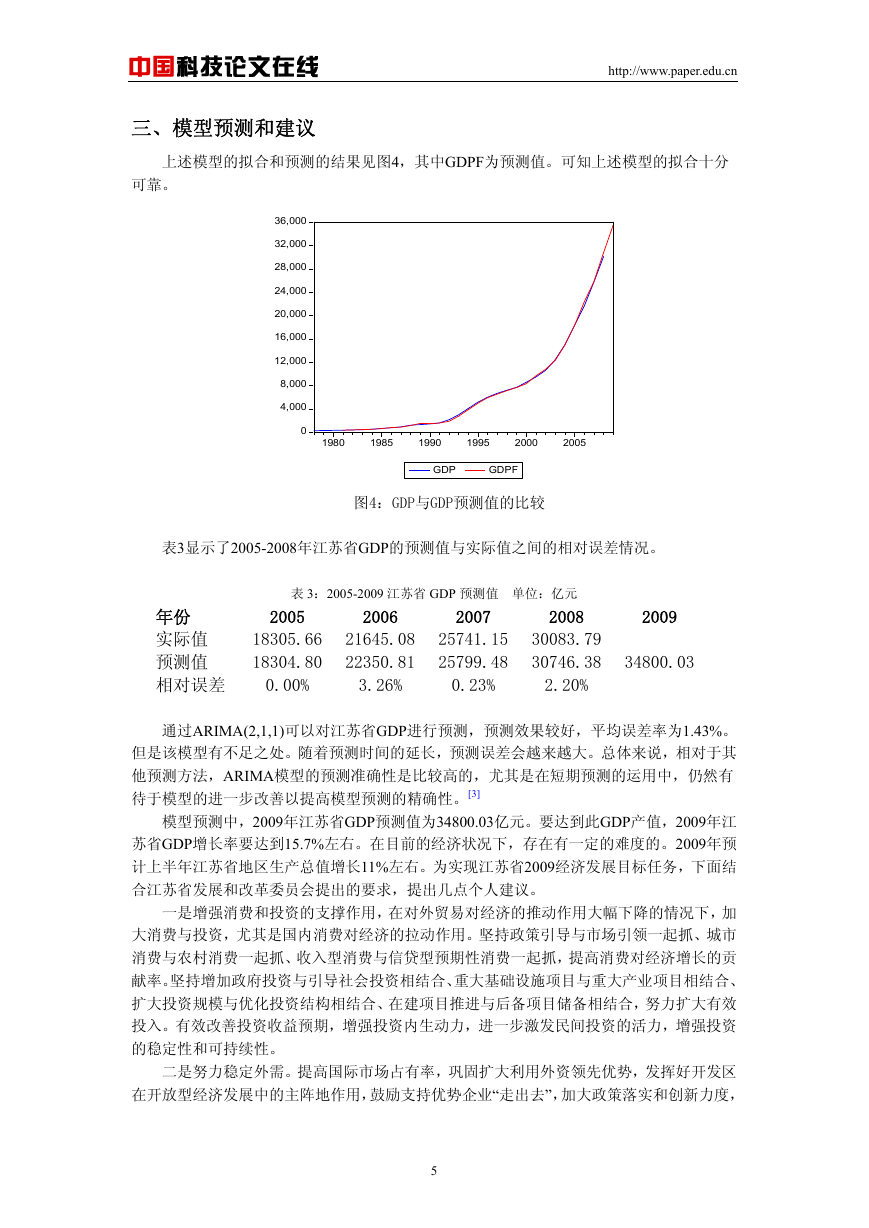
中国科技论文在线三、模型预测和建议 http://www.paper.edu.cn 上述模型的拟合和预测的结果见图4，其中GDPF为预测值。可知上述模型的拟合十分可靠。 36,000 32,000 28,000 24,000 20,000 16,000 12,000 8,000 4,000 0 1980 1985 1990 1995 2000 2005 GDP GDPF 图4：GDP与GDP预测值的比较表3显示了2005-2008年江苏省GDP的预测值与实际值之间的相对误差情况。表 3：2005-2009 江苏省 GDP 预测值单位：亿元 2005 2006 2007 2008 0.00% 18305.66 21645.08 25741.15 30083.79 18304.80 22350.81 25799.48 30746.38 34800.03 年份实际值预测值相对误差通过ARIMA(2,1,1)可以对江苏省GDP进行预测，预测效果较好，平均误差率为1.43%。但是该模型有不足之处。随着预测时间的延长，预测误差会越来越大。总体来说，相对于其他预测方法，ARIMA模型的预测准确性是比较高的，尤其是在短期预测的运用中，仍然有待于模型的进一步改善以提高模型预测的精确性。[3] 2.20% 3.26% 0.23% 2009 模型预测中，2009年江苏省GDP预测值为34800.03亿元。要达到此GDP产值，2009年江苏省GDP增长率要达到15.7%左右。在目前的经济状况下，存在有一定的难度的。2009年预计上半年江苏省地区生产总值增长11%左右。为实现江苏省2009经济发展目标任务，下面结合江苏省发展和改革委员会提出的要求，提出几点个人建议。一是增强消费和投资的支撑作用，在对外贸易对经济的推动作用大幅下降的情况下，加大消费与投资，尤其是国内消费对经济的拉动作用。坚持政策引导与市场引领一起抓、城市消费与农村消费一起抓、收入型消费与信贷型预期性消费一起抓，提高消费对经济增长的贡献率。坚持增加政府投资与引导社会投资相结合、重大基础设施项目与重大产业项目相结合、扩大投资规模与优化投资结构相结合、在建项目推进与后备项目储备相结合，努力扩大有效投入。有效改善投资收益预期，增强投资内生动力，进一步激发民间投资的活力，增强投资的稳定性和可持续性。二是努力稳定外需。提高国际市场占有率，巩固扩大利用外资领先优势，发挥好开发区在开放型经济发展中的主阵地作用，鼓励支持优势企业“走出去”，加大政策落实和创新力度， 5

中国科技论文在线把外需不足的不利影响减到最低。 http://www.paper.edu.cn 三是巩固扩大工业回升势头，夯实经济增长的基础。加大政策支持、要素保障和工作推进力度，充分发挥工业优化升级实施和产业调整振兴规划的引领指导作用，优化产业布局，强化产业特色，落实关键产业链提升计划，培育新的增长点，推动工业经济开启新一轮更高水平的增长。四是更大力度推进自主创新，加快转变经济发展方式。把保增长与调结构更加紧密地结合起来，大力推进产业优化升级，培育自主知识产权和自有品牌。[4] 参考文献： [1]毛春元黄萍江苏省 GDP 的 ARIMA 模型的研究和应用[J] 2008(2) 商场现代化 [2]孙敬水中级计量经济学[M] 2008(7) 上海财经大学出版社 [3]高铁梅计量经济分析方祛与建模[M] 2006 清华大学出版社 [4]江苏省发改委要闻发布江苏省发展和改革委员会 2009(7) The Application of ARIMA model in the Prediction of GDP of Jiangsu Province ZHAO WEI Economy and management school of Southeast University Nanjing 211189 H H UCmes1988@163.comU Abstract：This paper uses time-series prediction methods synthetically to establish a time series auto regressive and moving average model(AEIMA) for the GDP of Jiangsu province from 1978 to 2008. The analysis shows that ARIMA(2,1,1) model provides comparatively precise estimation results which can offer a reasonable basis for the prediction of the GDP of Jiangsu province in 2009. At last, this paper presents several political suggestions for the development of Jiangsu economy on the basis of the analysis results. Keywords: ARIMA model GDP prediction time-series 6T T

资料库

ARIMA模型在江苏省GDP预测中的运用.pdf

相关推荐

开发技术

热门标签

最新资料