logo资料库

模式识别结业论文.doc

发布时间：2022-06-20 发布人：admin 分类：说明书 资料大小：0.33M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    基于 libsvm 的手写字体识别 一、实验目的 1.对模式识别有一个初步的理解。 2.理解 SVM 分类的基本原理。 3.掌握用 MATLAB 软件设计 SVM 分类器，通过特征提取、分类器设计实现 简单的手写体数字图像识别系统，并对系统进行评估。 二、实验条件 MATLAB 软件。 三、实验原理 1. SVM 的基本原理 SVM 方法是通过一个非线性映射φ，把样本空间映射到一个高维乃至无穷维 的特征空间中（Hilbert 空间），使得在原来的样本空间中非线性可分的问题转化 为在特征空间中的线性可分的问题。简单地说，就是升维和线性化。升维，就是 把样本向高维空间做映射，一般情况下这会增加计算的复杂性，甚至会引起“维 数灾难”，因而人们很少问津。但是作为分类、回归等问题来说，很可能在低维 样本空间无法线性处理的样本集，在高维特征空间中却可以通过一个线性超平面 实现线性划分（或回归）。一般的升维都会带来计算的复杂化，SVM 方法巧妙地 解决了这个难题：应用核函数的展开定理，就不需要知道非线性映射的显式表达 式；由于是在高维特征空间中建立线性学习机，所以与线性模型相比，不但几乎 不增加计算的复杂性，而且在某种程度上避免了“维数灾难 ”。这一切要归功于 核函数的展开和计算理论。 选择不同的核函数，可以生成不同的 SVM，常用的核函数有以下 4 种： （1）线性核函数 ( , K x y （2）多项式核函数 ( , K x y   ； x y x y  ) 1] d ； [(  ) ) ( , K x y )  exp(  （3）径向基函数 （4）二层神经网络核函数 ( , K x y 2 ) x y  2  ； tanh( ( a x y  ) b ) 。 )  1
    2. MATLAB 自带的 svm 实现函数与 libsvm 的差别 （1）MATLAB 自带的 svm 实现函数仅有的模型是 C-SVC (C-support vector classification) ； 而 libsvm 工 具 箱 有 C-SVC (C-support vector classification) ， nu-SVC (nu-support vector classification)，one-class SVM (distribution estimation)， epsilon-SVR (epsilon-support vector regression) ， nu-SVR (nu-support vector regression) 等多种模型可供使用。 （2）MATLAB 自带的 svm 实现函数仅支持分类问题，不支持回归问题；而 libsvm 不仅支持分类问题，亦支持回归问题。 （3）MATLAB 自带的 svm 实现函数仅支持二分类问题，多分类问题需按照 多分类的相应算法编程实现；而 libsvm 采用 1v1 算法支持多分类。 （4）MATLAB 自带的 svm 实现函数采用 RBF 核函数时无法调节核函数的 参数 gamma，貌似仅能用默认的；而 libsvm 可以进行该参数的调节。 （5）libsvm 中的二次规划问题的解决算法是 SMO；而 MATLAB 自带的 svm 实现函数中二次规划问题的解法有三种可以选择：经典二次方法；SMO；最小 二乘。 在以上的一些对比下，我个人建议目前 svm 的实现还是使用 libsvm（这个 应该是目前最好用的 svm 工具箱），当然 MATLAB 自带的 svm 实现函数对于简 单问题也可使用。MATLAB 自带的 svm 实现函数可能会在更加新的版本里面进 行完善，目前可以用 MATLAB 自带的 svm 实现函数来进行重新封装实现 libsvm 中的所有功能，但工作量有些大。 四、实验内容 手写体阿拉伯数字识别是图像处理和模式识别领域中的研究课题之一。字符 识别系统一般由图像采集、信号预处理、特征提取、分类识别等几个部分组成。 识别系统的识别方式可分为联机手写体字符识别、脱机印刷体字符识别和脱机手 写体字符识别等，其中脱机手写体字符由于书写者的因素，使其字符图像的随意 性很大，例如，笔画的粗细、字体的大小、手写体的倾斜度、字符笔画的局部扭 曲变形、字体灰度的差异等都直接影响到字符的正确识别。所以，手写体数字字 符的识别是数字字符识别领域内最具挑战性的课题。 近年来，支持向量机（Support Vector Machines，SVM）的研究在广泛开展。 2
    支持向量机是 V.Vipnik 等人根据统计学习理论(Statistic Learning Theory，SLT)提 出的一种新的机器学习方法，在解决小样本、非线性及高维模式识别问题中表现 出许多特有的优势，已经在模式识别、函数逼近和概率密度估计等方面取得了良 好的效果。 该实验尝试基于 SVM 进行 0～9 手写体阿拉伯数字的识别。讨论相关的数 字图像预处理、特征提取、分类器设计和系统评估等方面的问题，并给出相应的 解决方案，指出需要进一步改进的地方。 五、数据来源 本实验是对已经扫描后的手写体数字图像进行识别。图像用的是《MATLAB 高效编程技巧与应用：25 个案例分析》和《MATLAB 统计分析与应用：40 个案 例分析》中的手写字体的训练样本和测试样本。 图 1 训练数据掠影 图 2 测试数据掠影 3
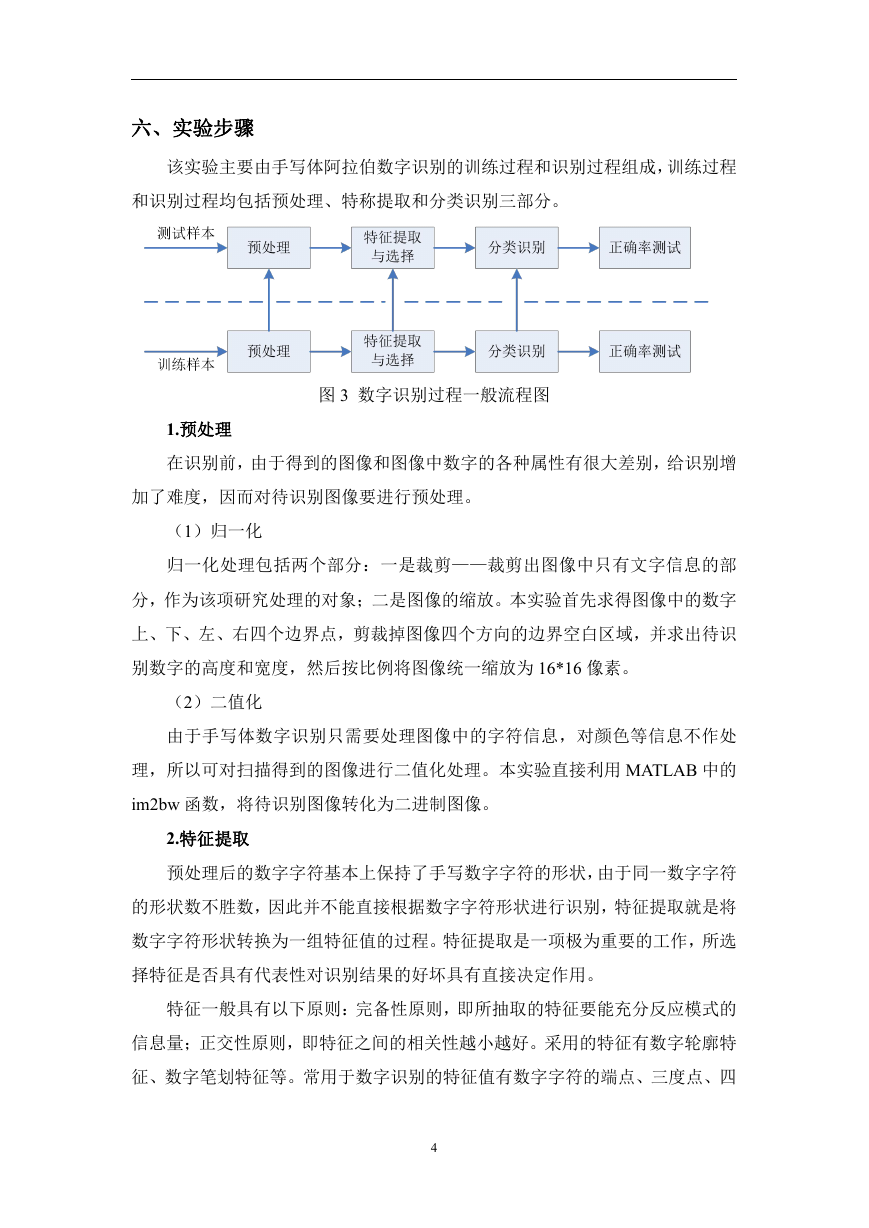
    六、实验步骤 该实验主要由手写体阿拉伯数字识别的训练过程和识别过程组成，训练过程 和识别过程均包括预处理、特称提取和分类识别三部分。 图 3 数字识别过程一般流程图 1.预处理 在识别前，由于得到的图像和图像中数字的各种属性有很大差别，给识别增 加了难度，因而对待识别图像要进行预处理。 （1）归一化 归一化处理包括两个部分：一是裁剪——裁剪出图像中只有文字信息的部 分，作为该项研究处理的对象；二是图像的缩放。本实验首先求得图像中的数字 上、下、左、右四个边界点，剪裁掉图像四个方向的边界空白区域，并求出待识 别数字的高度和宽度，然后按比例将图像统一缩放为 16*16 像素。 （2）二值化 由于手写体数字识别只需要处理图像中的字符信息，对颜色等信息不作处 理，所以可对扫描得到的图像进行二值化处理。本实验直接利用 MATLAB 中的 im2bw 函数，将待识别图像转化为二进制图像。 2.特征提取 预处理后的数字字符基本上保持了手写数字字符的形状，由于同一数字字符 的形状数不胜数，因此并不能直接根据数字字符形状进行识别，特征提取就是将 数字字符形状转换为一组特征值的过程。特征提取是一项极为重要的工作，所选 择特征是否具有代表性对识别结果的好坏具有直接决定作用。 特征一般具有以下原则：完备性原则，即所抽取的特征要能充分反应模式的 信息量；正交性原则，即特征之间的相关性越小越好。采用的特征有数字轮廓特 征、数字笔划特征等。常用于数字识别的特征值有数字字符的端点、三度点、四 4
    度点、折点的个数与位置，有横向切割交点序列、纵向切割交点序列等。在这一 过程中，被认为是非特征值的像素点被忽略掉。 本实验中，由于预处理后的图像都是 16*16 大小的，所以我们把图像分成了 16*16= 256 个小格子，把每个格子里的像素值作为一个分量，形成一个 256 维的 矢量，将该矢量作为图像的特征向量。 3.分类识别 利用支持向量机进行手写体数字识别的分类函数形式上类似一个神经网络， 其输出是若干中间层节点的线性组合，而每一个中间层节点对应于输入样本与一 个支持向量的内积，因此也称为支持向量网络。 由于 SVM 是二分类器，如果要识别 0～9 的数字必须要多个 SVM 分类器组 合起来使用，这样工作量比较大，因此，本实验采用的是在 MATLAB 的基础上， 结合 libsvm 中的训练程序 svmtrain 和识别程序 svmpredict，利用 libsvm 加强工 具箱利用 GA（或者 gridsearch）来实现参数寻优，采用的核函数为 RBF 核函数。 本实验对每个字符提取了 5 个训练样本，所以共有 10 组样本，总共有 50 个训练样本。将每个字符对应的训练样本输入，程序将自动提取待识别图像的特 征，形成向量，进行训练。训练完成后，将测试图像输入，测试图像中，每个字 符有 3 个测试样本，共 10 组，总共有 30 个测试样本，程序自动进行特征提取后， 形成向量并分类。 七、实验代码 function CharacterRecognitionLibsvm % Character Recognition based on libsvm %% tic; close all; clear; clc; format compact; %% 载入训练数据 [FileName,PathName,FilterIndex] = uigetfile( ... 5
    {'*.jpg';'*.bmp'},'请导入训练图片','*.jpg','MultiSelect','on'); if ~FilterIndex return; end num_train = length(FileName); TrainData = zeros(num_train,16*16); TrainLabel = zeros(num_train,1); for k = 1:num_train pic = imread([PathName,FileName{k}]); pic = pic_preprocess(pic); TrainData(k,:) = double(pic(:)'); TrainLabel(k) = str2double(FileName{k}(4)); end %% 建立支持向量机 % [bestCVaccuracy,bestc,bestg] = ... % SVMcgForClass(TrainLabel,TrainData,-8,8,-8,8,10,0.8,0.8,4.5) ga_option.maxgen = 100; ga_option.sizepop = 20; ga_option.cbound = [0,100]; ga_option.gbound = [0,100]; ga_option.v = 10; ga_option.ggap = 0.9; [bestCVaccuracy,bestc,bestg] = ... gaSVMcgForClass(TrainLabel,TrainData,ga_option) cmd = ['-c ',num2str(bestc),' -g ',num2str(bestg)]; model = svmtrain(TrainLabel, TrainData, cmd); preTrainLabel = svmpredict(TrainLabel, TrainData, model); 6
    %% 载入测试样本 [FileName,PathName,FilterIndex] = uigetfile( ... {'*.jpg';'*.bmp'},'Çëµ¼Èë²âÊÔͼƬ','*.bmp','MultiSelect','on'); if ~FilterIndex return; end num_train = length(FileName); TestData = zeros(num_train,16*16); TestLabel = zeros(num_train,1); for k = 1:num_train pic = imread([PathName,FileName{k}]); pic = pic_preprocess(pic); TestData(k,:) = double(pic(:)'); TestLabel(k) = str2double(FileName{k}(4)); end %% 对测试样本进行分类 preTestLabel = svmpredict(TestLabel, TestData, model); assignin('base','TestLabel',TestLabel); assignin('base','preTestLabel',preTestLabel); TestLabel' preTestLabel' %% sub function of pre-processing pic function pic_preprocess = pic_preprocess(pic) pic = 255-pic; pic = im2bw(pic,0.4); [y,x] = find(pic == 1); pic_preprocess = pic(min(y):max(y), min(x):max(x)); pic_preprocess = imresize(pic_preprocess,[16,16]); %% % toc; 7
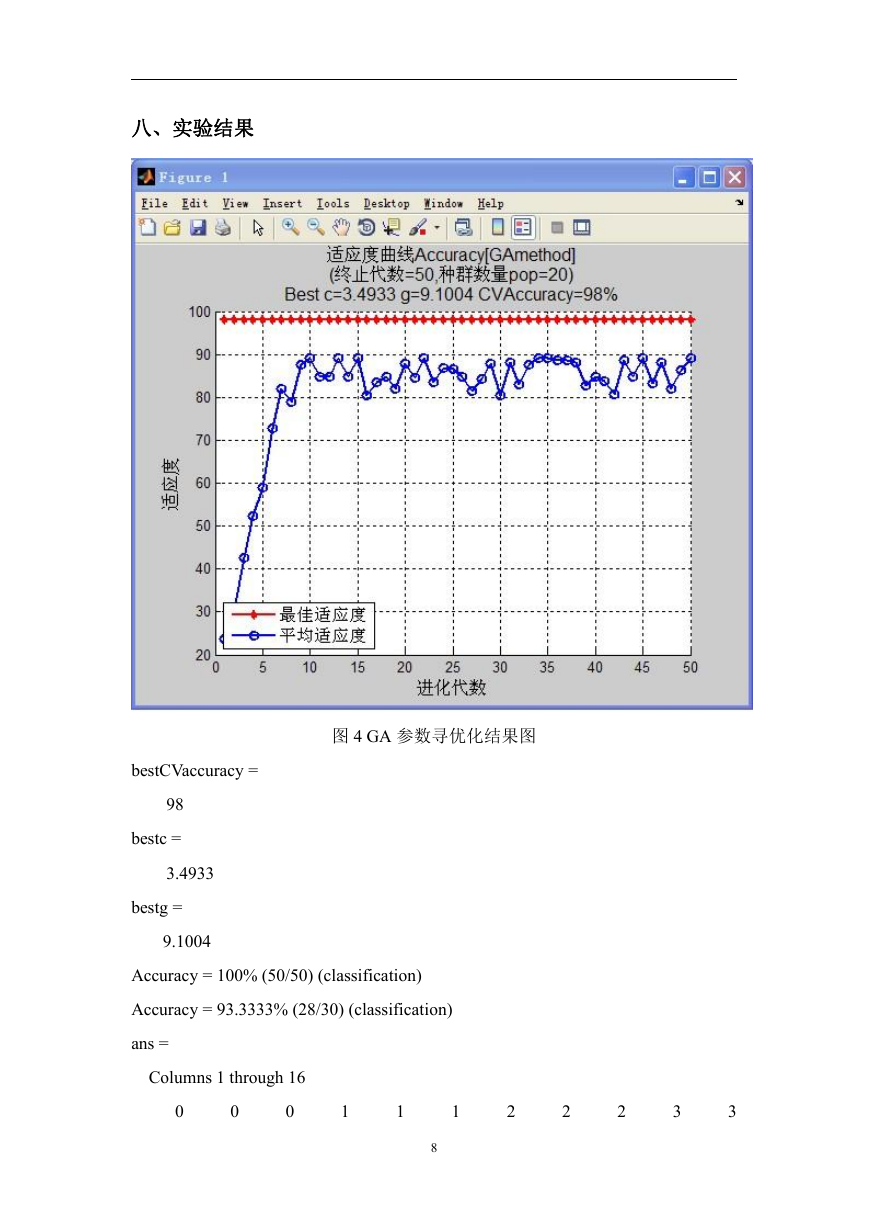
    八、实验结果 图 4 GA 参数寻优化结果图 bestCVaccuracy = 98 bestc = 3.4933 bestg = 9.1004 Accuracy = 100% (50/50) (classification) Accuracy = 93.3333% (28/30) (classification) ans = Columns 1 through 16 0 0 0 1 1 1 2 2 2 3 3 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    大数据

    共收录841份资料，累计11个分类，关注成员有19位，主要包括：Matlab,统计分析,数据挖掘,Hbase,Hive,flink,kafka,spark,Storm,算法与数据结构,Hadoop

    热门标签

    Matlab 统计分析 数据挖掘 Hbase Hive flink kafka spark Storm 算法与数据结构 Hadoop

    最新资料