logo资料库

vegan中文教程.pdf

发布时间：2022-06-18 发布人：admin 分类：说明书 资料大小：3.01M 资料格式：pdf 举报 版权申诉
第1页 / 共50页
第2页 / 共50页
第3页 / 共50页
第4页 / 共50页
第5页 / 共50页
第6页 / 共50页
第7页 / 共50页
第8页 / 共50页
资料共50页，剩余部分请下载后查看
    生态群落多元分析 R 程序包 vegan 教程 Jari Oksanen 2015.6.10 摘要 本教程演示了生态群落数据多元分析 R 语言程序包 vegan 的排序分析方法， 学习本教程之前您应了解 R 语言基本语法和群落排序的一般概念。vegan 包提供 包括非度量多维尺度分析（NMDS）在内的所有基本排序方法。教程也介绍了包 括邻近约束分析（CAP），冗余分析（RDA）和典范对应分析（CCA）等约束排 序方法。vegan 包还提供环境变量拟合以及绘制排序图的函数。 目录 1 简介 ......................................................................................................................................................................2 2 基本的排序方法 ..............................................................................................................................................2 2.1 非度量多维尺度分析 .........................................................................................................................2 2.2 群落相异性 ...........................................................................................................................................5 2.3 比较排序图：普氏旋转（Procrustes rotation） ...................................................................8 2.4 特征向量法 ........................................................................................................................................9 2.5 去趋势对应分析（DCA） ............................................................................................................ 12 2.6 排序图 ................................................................................................................................................. 14 3 使用环境因子被动解释排序轴 ............................................................................................................... 16 3.1 矢量拟合 ............................................................................................................................................ 17 3.2 曲面拟合 ............................................................................................................................................ 18 3.3 因子变量 ............................................................................................................................................ 19 4 约束排序 ......................................................................................................................................................... 21 4.1 模型说明 ............................................................................................................................................ 22 4.2 置换检验 ............................................................................................................................................ 25 4.3 模型建立 ............................................................................................................................................. 27 4.4 线性组合和加权平均 ...................................................................................................................... 33 1. 线性组合坐标 lc：约束变量的线性组合。 .................................................................. 33 2. 加权平均坐标 wa：物种坐标的加权平均。 ................................................................ 33 4.5 双序图箭头和环境标定 ................................................................................................................. 34 4.6 条件模型或偏模型 ........................................................................................................................... 35 5 相异性与环境 ................................................................................................................................................. 37 5.1 adonis：基于相异矩阵的多元方差分析 .................................................................................. 38 5.2 组的同质性和 beta 多样性 ........................................................................................................... 39 5.3 Mantel 检验....................................................................................................................................... 41 5.4 Protest:普鲁克检验 .......................................................................................................................... 43 6 分类 ................................................................................................................................................................... 44 6.1 聚类分析 ............................................................................................................................................ 44 6.2 类的显示和解释 .............................................................................................................................. 46 6.3 分类群落表 ......................................................................................................................................... 49 1
    1 简介 本教程演示了生态群落数据多元排序分析的操作流程。首先讨论了非约束排 序分析以及基于其结果的环境解释（此时环境因子不参与排序过程）。然后以典 范对应分析（CCA）为例介绍了约束排序，类似地，邻近约束分析（constrained analysis of proximities，CAP）和冗余分析（RDA）等方法也可以进行相同的排序 分析。最后，本教程介绍了不基于排序的物种-环境关系的分析方法以及群落的 聚类分析。 教程中的案例是经过检验的：这是一个 Sweave 文档（基于 LaTeX 的 R 代码 组织的文档）。源文件只包含文本和 R 命令：结果和统计图表的输出需要通过运 行 Sweave 源文件时生成。本文档中 R 是 2015-06-09 的版本(vegan 2.3-0 版本)， 其实 vegan 和 R 也在不断发展中。 教程主要涵盖了 vegan 包的排序方法，没有介绍 vegan 包其他同样重要的函 数，例如生物多样性分析函数：多样性指数(diversity()、renyi()、fisher.alpha())、 物种丰富度(specpool(), estimate())、物种积累曲线(specaccum())、物种丰富度模型 (radfit()、fisherfit()、prestonfit())等。vegan 也不是唯一能进行生态群落多元分析 的 R 语言工具。R 语言基础包有标准的统计工具，labdsv 包提供一些高级方法或 替代函数对 vegan 进行了补充，ade4 是利用欧几里得方法进行生态学数据分析的 包。 本教程仅介绍了基本的方法，并展示了常用案例的一般流程。我们认为排序 方法主要是作为一种图形工具，所以没有花太多精力展示精确的数值，取而代之 的是在绘图命令旁边穿插绘制结果。建议您参考本教程尝试自己的分析，探索不 同的替代方案，并花时间去理解命令以及函数的输出结果。教程仅对函数作了简 要的说明，如果想获得更全面的解释，请查看相应的帮助文档。需要注意本文档 也只是为了应用相应的函数而写的，想获得更坚实的理论背景，最好的方法是查 阅有关生态学群落排序方法的教科书或者学习相关的课程。 2 基本的排序方法 2.1 非度量多维尺度分析 非度量多维尺度分析（Non-metric multidimensional scaling, NMDS）可以用 MASS 包中的 isoMDS()函数实现，输入相异矩阵即可。vegan 的 vegdist()函数可 以计算群落的相异矩阵，默认是 Bray-Curtis 相异系数，现在通常称为 Steinhaus 相似指数，在芬兰称为 Sorensen 指数。基本步骤如下: > library(vegan) > library(MASS) 2
    > data(varespec) > vare.dis <- vegdist(varespec) > vare.mds0 <- isoMDS(vare.dis) NMDS排序结构通过迭代来不断最小化应力函数（stress function），默认情 况下是找到两个维度并使用度量尺度分析(cmdscale)作为初始结构进行调整。从 跟踪(trace)信息中可以看出迭代过程(通过设置参数trace = F来隐藏迭代过程)。 isoMDS()返回一个排序构建过程和应力函 数的列表(item points, stress)。 S应力函数是一个拟合度统计量，是排序空 间内对象结构与原始距离矩阵之间的相异程度 的度量。 NMDS将观察到的群落差异非线性地映射 到排序空间上，可以基于任何类型距离矩阵对 对象进行排序。可以用MASS包的函数 Shepard()或者vegan包的stressplot()函数来评估 NMDS的结果（Shepard图）。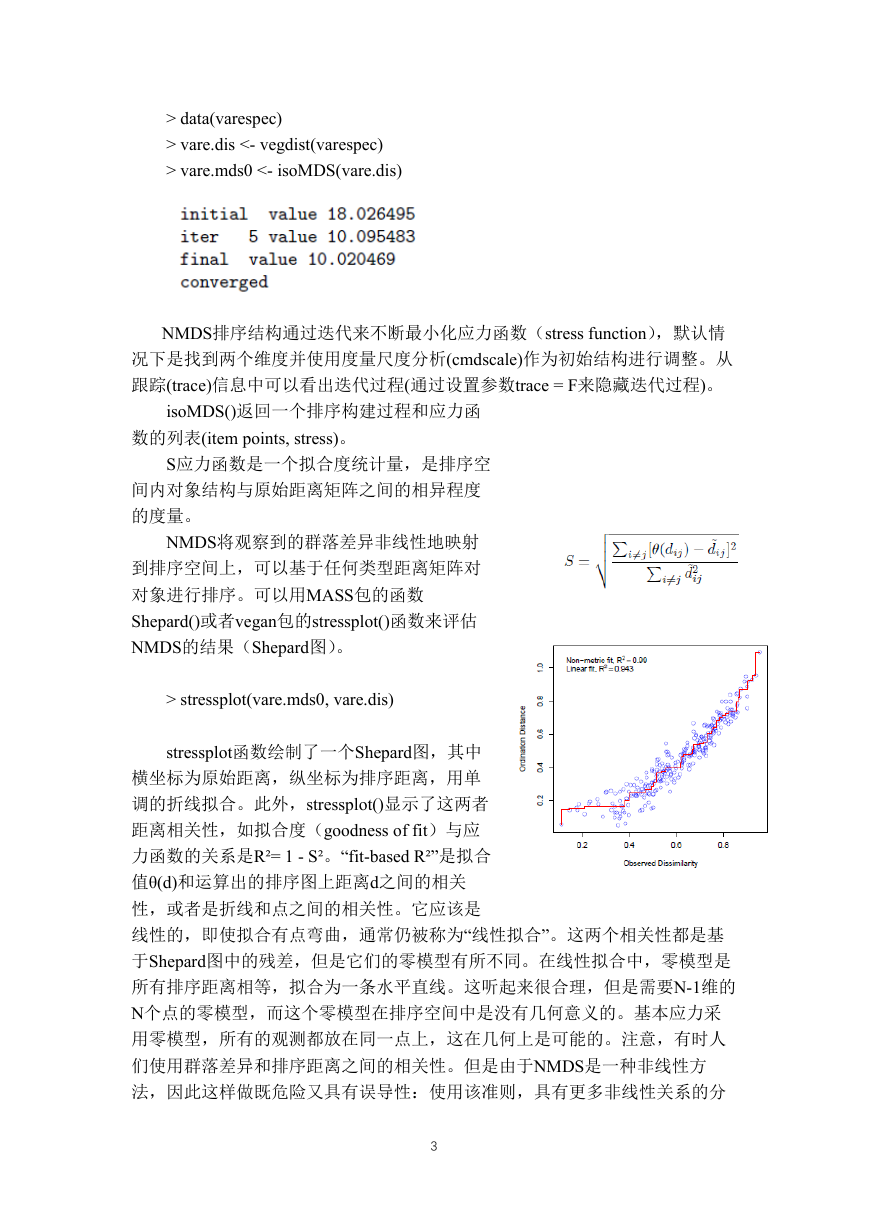 > stressplot(vare.mds0, vare.dis) stressplot函数绘制了一个Shepard图，其中 横坐标为原始距离，纵坐标为排序距离，用单 调的折线拟合。此外，stressplot()显示了这两者 距离相关性，如拟合度（goodness of fit）与应 力函数的关系是R²= 1 - S²。“fit-based R²”是拟合 值θ(d)和运算出的排序图上距离d之间的相关 性，或者是折线和点之间的相关性。它应该是 线性的，即使拟合有点弯曲，通常仍被称为“线性拟合”。这两个相关性都是基 于Shepard图中的残差，但是它们的零模型有所不同。在线性拟合中，零模型是 所有排序距离相等，拟合为一条水平直线。这听起来很合理，但是需要N-1维的 N个点的零模型，而这个零模型在排序空间中是没有几何意义的。基本应力采 用零模型，所有的观测都放在同一点上，这在几何上是可能的。注意，有时人 们使用群落差异和排序距离之间的相关性。但是由于NMDS是一种非线性方 法，因此这样做既危险又具有误导性：使用该准则，具有更多非线性关系的分 3
    类将会出现更多错误。 vegan 的 ordiplot()函数可以用来绘制 NMDS 的结果： > ordiplot(vare.mds0, type = "t") 相异矩阵没有物种的信息，因此只显示了样方信息（site）。 由于排序轴与初始相异结构之间存在非线性关 系，使得 NMDS 在迭代时最优化应力函数非常 困难：迭代容易陷入局部最优而不是全局最优。 因此，建议进行多次独立的尝试，并在应力函数 （stress）最小的类似解决方案中选择初始结构。 这 样 做 可 能 会 很 耗 精 力 ， 好 在 vegan 有 metaMDS()函数可以做到这一点。迭代过程输出 很长，可以设置 trace = FALSE 来隐藏迭代过程 显示，但通常我们希望有变化发生，尽管分析可 能需要很长时间： > vare.mds <- metaMDS(varespec, trace = FALSE) > vare.mds > plot(vare.mds, type = "t") 4
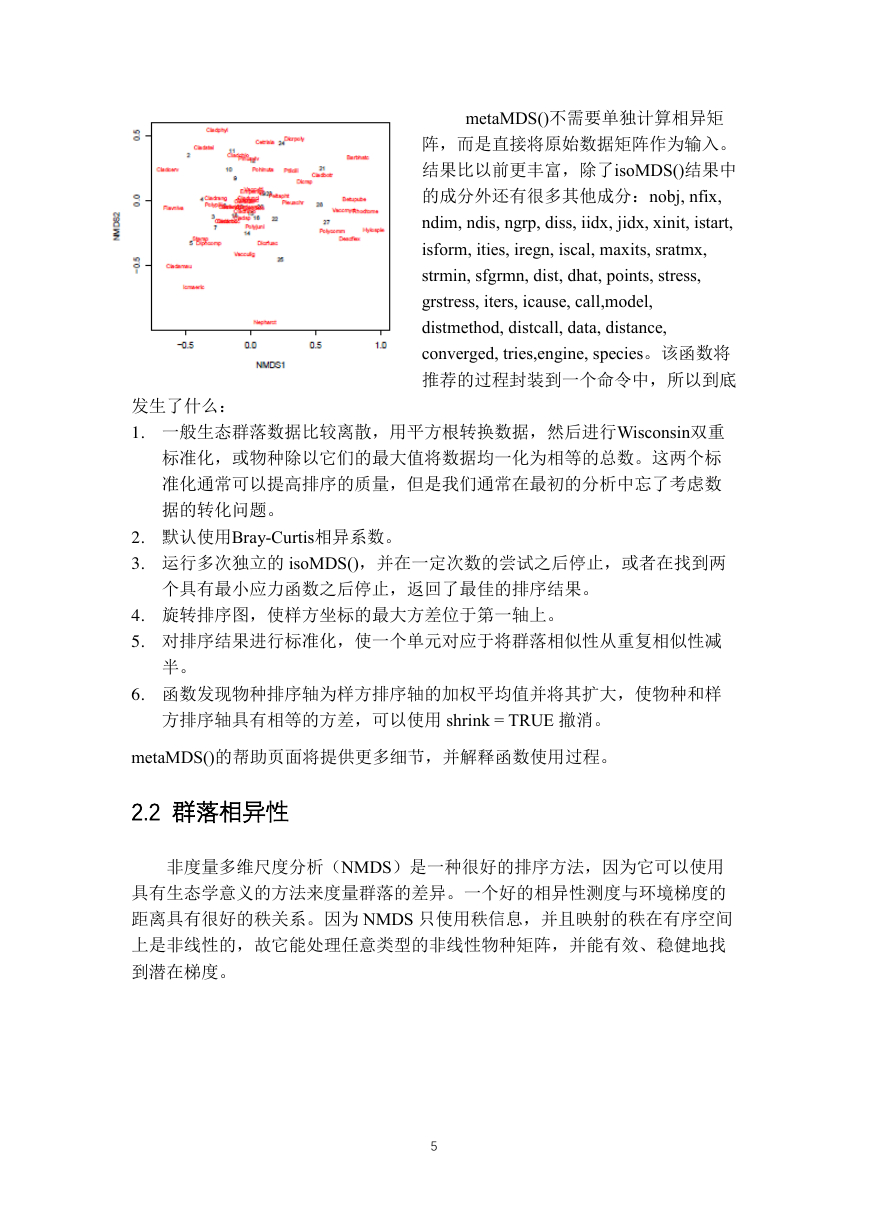
    metaMDS()不需要单独计算相异矩 阵，而是直接将原始数据矩阵作为输入。 结果比以前更丰富，除了isoMDS()结果中 的成分外还有很多其他成分：nobj, nfix, ndim, ndis, ngrp, diss, iidx, jidx, xinit, istart, isform, ities, iregn, iscal, maxits, sratmx, strmin, sfgrmn, dist, dhat, points, stress, grstress, iters, icause, call,model, distmethod, distcall, data, distance, converged, tries,engine, species。该函数将 推荐的过程封装到一个命令中，所以到底 发生了什么： 1. 一般生态群落数据比较离散，用平方根转换数据，然后进行Wisconsin双重 标准化，或物种除以它们的最大值将数据均一化为相等的总数。这两个标 准化通常可以提高排序的质量，但是我们通常在最初的分析中忘了考虑数 据的转化问题。 2. 默认使用Bray-Curtis相异系数。 3. 运行多次独立的 isoMDS()，并在一定次数的尝试之后停止，或者在找到两 个具有最小应力函数之后停止，返回了最佳的排序结果。 4. 旋转排序图，使样方坐标的最大方差位于第一轴上。 5. 对排序结果进行标准化，使一个单元对应于将群落相似性从重复相似性减 半。 6. 函数发现物种排序轴为样方排序轴的加权平均值并将其扩大，使物种和样 方排序轴具有相等的方差，可以使用 shrink = TRUE 撤消。 metaMDS()的帮助页面将提供更多细节，并解释函数使用过程。 2.2 群落相异性 非度量多维尺度分析（NMDS）是一种很好的排序方法，因为它可以使用 具有生态学意义的方法来度量群落的差异。一个好的相异性测度与环境梯度的 距离具有很好的秩关系。因为 NMDS 只使用秩信息，并且映射的秩在有序空间 上是非线性的，故它能处理任意类型的非线性物种矩阵，并能有效、稳健地找 到潜在梯度。 5
    最自然的相异性测度是欧氏距离，欧氏距离是许多特征向量排序方法默认 相异测度，它是物种空间中的距离。物种空间是指每个物种都是一个与所有其 他物种正交的轴，而样方是这个多维超空间中的点。然而，欧氏距离是基于差 值的平方，受单个最大方差影响较大。因此大多数有生态意义的相异系数是曼 哈顿（Manhattan）类型的，使用的是差值而不是差值的平方。良好的相异指数 的另一个特征是百分数系数：如果两个群落没有相同的物种，它们的相异指数 最大，即为 1。另外，即使没有相同的物种，欧氏和曼哈顿相异指数也会随总 体物种丰度的变化而变化。 vegan 包有 vegdist()函数可以计算各类相异系数，包 括 Bray-Curtis、Jaccard 和 Kulczyński 指数。所有这些都 属于曼哈顿类型，只使用一阶项（和以及差值），所有这 些都按样方总数进行相对化，并在两个被比较群落之间没 有相同物种时达到最大值 1。vegdist()函数是 R 基础 dist() 函数的一个简易替代，这两个函数都可以用于相异系数的 计算。 众多的相异指数有许多令人困惑的方面：一是同样的 指数名称却可能有完全不同的表达式：以右图曼哈顿相异 系数的两种可选择的表达式为例。另一个复杂的问题是命 名，vegdist()函数使用不够严格的口语化名字。vegan 的 默认指数是 Bray（或 Bray-Curtis），但它可能应该被称为 Steinhaus 指数，几年前它的名字是 Czekanowski 指数（但 现在这被认为是另一个指数），它也被称为 Sørensen 指数 （但经常拼写错误）。严格来说，Jaccard 是二元（有-无）系数，但其定量版本 在在 vegan 包称为 Ružička 指数。 这三个基本指标在梯度度量中被认为是较好的。此外，vegdist()函数还能够 计算其他类型的距离矩阵：Morisita、Horn-Morisita、Raup-Cric、Binomial 和 Mountford 指数能够比较不同抽样单位的相异性，而 Euclidean、Canberra 和 Gower 指数具有更好的理论基础。 metaMDS()函数使用 Bray-Curtis 相异系数作为默认值，这通常是一个不错 的选择。Jaccard （Ružička）指数具有完全相同秩的序，但具有更好的度量属 性，可能应该作为首选。rankindex()函数在 vegan 中使用秩相关作为默认值，可 用来研究哪个指数最好地沿着已知的梯度分离群落。下面的例子使用了 varechem 数据集中的所有环境变量，但都将其标准化为单位方差：是非线性相 关的，但它们的秩的序是相同的，因此它们的秩相关也是相同的。一般来说， 这三个推荐的指标是相当一致的。 > data(varechem) 6
    > rankindex(scale(varechem), varespec, c("euc","man","bray","jac","kul")) 许多教科书强调指标的度量性质，这些在某些方法中很重要，但在只使用 信息的 NMDS 中就不重要了。这些度量属性简单来说是： 1. 如果两个样方相同，它们的距离为零； 2. 如果两个样方不同，它们的距离大于零； 3. 距离是对称的； 4. 两个样方之间最短的距离是直线，不受其他样方的 影响。 这些条件听起来都很自然，但并不是所有的相异系数都能满足。实际上， 只有欧氏距离——可能还有 Jaccard 指数——满足这里讨论的相异系数的所有条 件，并且是度量性质的。许多其他的相异系数满足前三个条件，并且是半度量 性质的。 有一个学派说我们应该使用度量指标，并且首选的是欧氏距离。它们的缺 点之一是没有固定的界限，但是没有相同物种的两个样方的相异系数可能会不 同，甚至看起来比共有某些物种的两个样方更为相似。这可以通过标准化数据 来解决。由于欧氏距离是基于平方差的，一个自然的变换是将样方标准化为相 等的平方和，或者使用 decostand()函数将其标准化为向量范数： > dis <- vegdist(decostand(varespec, "norm"), "euclid") 当两个样方之间没有相同物种时，其弦距离达到最大值 。另一个推荐的 替代方法是 Hellinger 距离，它实际上是多度值先除以样方多度总和再取平方根 后计算的欧式距离： > dis <- vegdist(decostand(varespec, "hell"), "euclidean") 7 2
    即使进行了标准化处理，欧式距离仍然具有良好的特性，除了用于转换数 据之外。实际上即使使用其他指数，转换或标准化数据也常 常很有用。如果在最小的非零丰度和最大丰度之间存在较大 的差异，我们会想要减小这种差异，通常平方根变换足以平 衡数据。Wisconsin 双重标准化往往提高了相异系数的梯度 检测能力；这可以在 vegan 中使用函数 wisconsin()来实现。 在这里，我们首先将所有物种数分别除以它们的最大值，然 后将样方标准化到单位总量。在标准化之后，许多相异指数 在排序上变得相同，在 NMDS 中应得到相同的结果。 在 vegan 包中，不仅可以使用 vegdist()函数，vegdist() 与 R 的 dist()函数返回结构类似的相异矩阵，也可以使用标 准 R 的 dist()函数以及其他包里的兼容函数，如 dsvdis() （labdsv 包）、daisy()（cluster 包）和 distance()（analogue 包），以及 vegan 包 betadiver()中的 β 多样性指数。此外， vegan 有 designdist()函数，支持用上面的 A、B 和 J 的符号 来写它的方程，从而定义自己的相异系数，或者用二元数 据，2*2 列联表表示法，其中 a 是在两个比较样方发现的物 种数量，b 和 c 是只在其中一个样方发现的物种数量。以下 三个方程定义了相同的 Sørensen 指数，用共有物种的数量 除以比较样方的平均物种丰富度： > d <- vegdist(varespec, "bray", binary = TRUE) > d <- designdist(varespec, "(A+B-2*J)/(A+B)") > d <- designdist(varespec, "(b+c)/(2*a+b+c)", abcd=TRUE) Betadiver()函数在 vegan 中定义了更多的二元相异指数。 大多数已发表的相异指数可表示为 designdist 公式。但是，在现有函数中使 用固定的替代方法会更容易也更安全：在手动编写相异指数方程时很容易出 错。 2.3 比较排序图：普氏旋转（Procrustes rotation） 排序结果一般用排序图表示，比较两种排序方法构成的排序图是一个比较直 观的方法。两个排序结果可能非常相似，但是由于轴的方向和比例略有不同，它 们的差别很难观察到。实际上在 NMDS 中，虽然 metaMDS()使用简单的方法来 确定最后三个组分，但是轴的标尺、排序、比例和位置都还不确定。比较排序的 最好方法是使用普氏旋转(Procrustes rotation)。Procrustes rotation 使用均匀的比例 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料