logo资料库

徐州潘安湖风景区游览路线设计.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.92M 资料格式：docx 举报 版权申诉
第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
资料共14页，剩余部分请下载后查看
    徐州潘安湖风景区游览路线设计
    摘要
    徐州潘安湖风景区游览路线设计 摘要 本文针对徐州潘安湖风景区游览路线问题，利用最短路径算法，构建多个 模型以解决多个题目。 针对问题一，本文建立了模型 I—最短路径求解模型。根据题目要求计算 从景石出发，经过 1-6 所有景点最终到达湿地商业街的最短路径。依据最短路径 算法思想，考虑到该问题的背景是一个小型的湿地公园，只需经过 7 个，因而利 用 MATLAB 软件，采用暴力穷举模型，对总共 720 种可能进行对比分析，最终得 出最短路线的长度为 1820。 针对问题二，本文建立了模型 II—游览路线最优模型。考虑到要设置游览 时间最长，所以路径所消耗的时间要最短。根据步行速度 2 V  km h / ，以及森林 小剧场的开放时间这个约束条件，在问题一中利用贪心法，在问题一中的 720 种 可能中找到多个局部最优解，之后再对局部最优解进行穷举找出最优解，得出表 4 游览时间最长的路线信息结果。 针对问题三，本文建立了模型三—旅游团最优模型。根据题目的约束条件， 要为三个旅游团分别设计一条能游览完全部 7 个景点且游览总时间最长的路线， 并且每个景点同时只能容纳 1 个旅游团游览。以浏览时间最长为设计指标，建立 最优化方程，利用组合优化思想，对每个景点进行图化，设计加权网络图，将单 TSP 问题根据权值转换成 MTSP 问题[1]。之后利用遗传算法[2 计算多旅行商问题， 最后得出表 5 的旅行路线信息。 针对问题四，本文建立了模型……。考虑到题目在问题三的基础上，添加 步行速度以及总的等待时间短的约束条件。采用最优路径思想，建立双目标优化 模型，将两个目标综合起来，变成一个目标，从而减少目标数量，并且假设各个 旅游团的标准时间差相互独立，从而把每个旅游团的标准时间差相加，得出表 6 的路线信息。 针对问题五，
    关键词：写入关键词（3-5 个） 遗传算法 MTSP 穷举 图论 一、 问题重述 本题基于潘安湖景区的部分景点(如图 1 所示)，请在如下的假设下，完成徐 州潘安湖风景区游览路线设计问题。 假设： （1）任意两个景点之间的最短步行距离如表 1 给出。 （2）第二问、第三问假设步行速度 2 V  km h / 。 （3）游客在景区停留的时间由“景点之间的步行时间”、“景点游览时间（即 在景点内游玩的时间）” 和“在景区外的等待时间”三部分组成，其他时间忽略 不计，游览时间必须符合表 2 的要求。 1. 从景石出发，步行游览以下景点: ①游客服务中心，②阳光草坪，③森林小 剧场，④儿童科普体验区，⑤儿童戏水场，⑥湿地博物馆，⑦湿地商业街。 建立数学模型，找出从景石出发，到达⑦湿地商业街，并且经过①—⑥所有 景点至少 1 次的距离最短的路线，计算该路线的长度，并将相关结果填入表 格 3。注：在每个景点不用停留。 2. 如果某游客 12:00 从景石出发，要求他 17:00 前到达湿地商业街，17:30 离 开湿地商业街(注：根据表 2 的要求在湿地商业街游览时间至少为 30 分钟)。 建立数学模型，为该游客设计一条能游览完全部景点(景点①—⑦)且游览总 时间最长的游览路线（假设在各个景点没有等待时间），并完成表 4 的填写。 3. 如果有 3 个旅游团，12:00 同时从景石出发，要求三个旅游团 17:00 前到达 湿地商业街，17:30 离开湿地商业街(注：根据表 2 的要求在湿地商业街游览 时间至少为 30 分钟)，并且每个景点（湿地商业街除外）同时只能容纳 1 个
    旅游团游览，按照时间顺序后到达的旅游团，需要等待先到达的旅游团游览 结束之后才能开始游览。建立数学模型，为三个旅游团分别设计一条能游览 完全部 7 个景点且游览总时间最长的游览路线，并完成表 5 的填写。 4. 假设 3 个旅游团的步行速度可以在1 / km h 之间调节，但是总的平均 km h ，3 个旅游团 12:00 同时从景石出发，要求三个旅 km h 到3 / 步行速度不能超过 2 / 游团 17:00 前到达湿地商业街，17:30 离开湿地商业街(注：根据表 2 的要求 在湿地商业街游览时间至少为 30 分钟)，并且每个景点（湿地商业街除外） 同时只能容纳 1 个旅游团游览，按照时间顺序后到达的旅游团，需要等待先 到达的旅游团游览结束之后才能开始游览。建立数学模型，为三个旅游团分 别设计一条能游览完全部 7 个景点且游览总时间长，总的等待时间短的游览 路线，并完成表 6 的填写。 5. 在现实中，考虑如下两个不确定性因素 (1) 不同旅游团从景石出发的时间具有不确定性，例如，多个旅游团在不同 的时间从景石出发开始游览，在此情况下到达湿地商业街的时间可以顺 延。 (2) 每个景点的等待时间也存在不确定性因素，例如，旅游设施短时间的维 护和清理，或者受到散客客流的影响。 考虑上述两个不确定性因素，其它条件与问题 4 相同，建立数学模型， 为多个旅游团分别设计一条能游览完全部 7 个景点且游览总时间长，总的等 待时间短的游览路线。
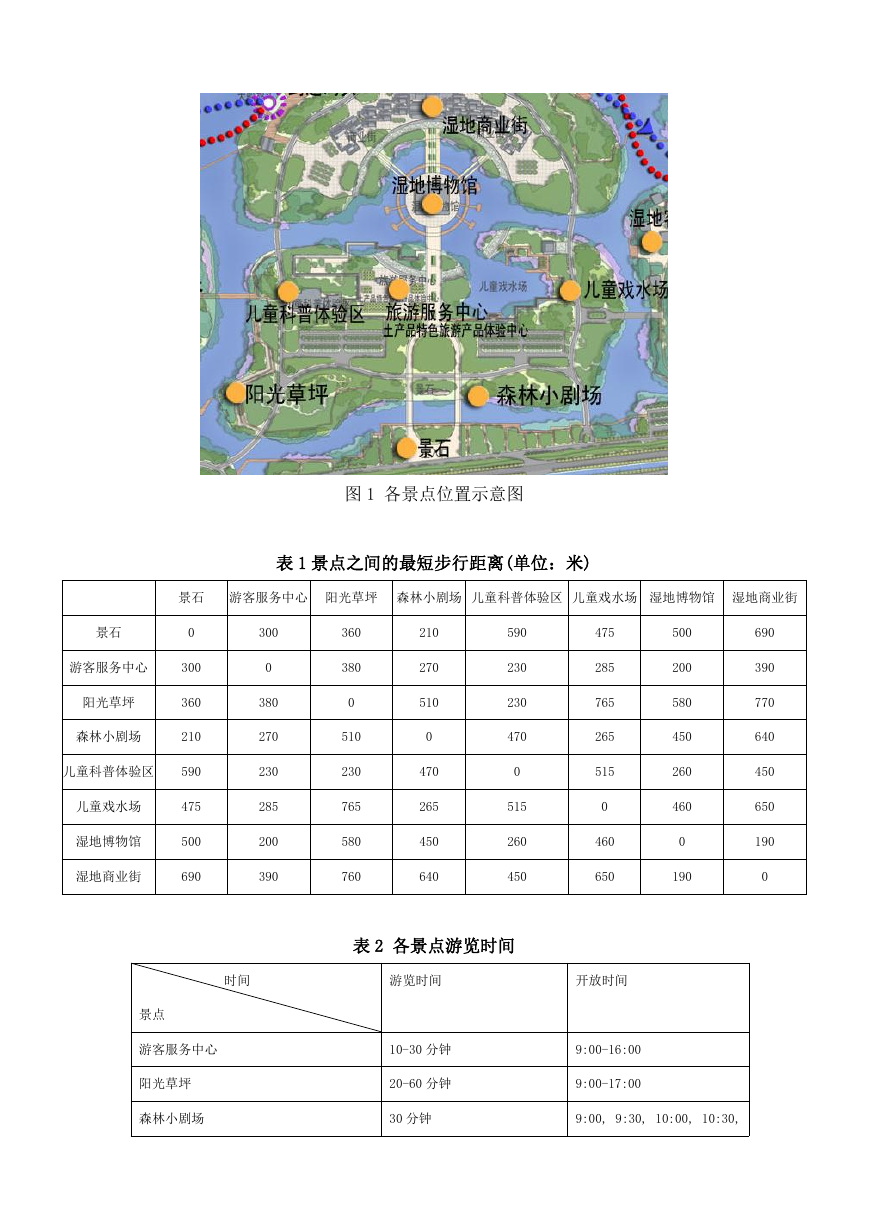
    图 1 各景点位置示意图 表 1 景点之间的最短步行距离(单位：米) 景石 游客服务中心 阳光草坪 森林小剧场 儿童科普体验区 儿童戏水场 湿地博物馆 湿地商业街 景石 游客服务中心 阳光草坪 森林小剧场 0 300 360 210 儿童科普体验区 590 儿童戏水场 湿地博物馆 湿地商业街 475 500 690 300 0 380 270 230 285 200 390 360 380 0 510 230 765 580 760 210 270 510 0 470 265 450 640 590 230 230 470 0 515 260 450 475 285 765 265 515 0 460 650 500 200 580 450 260 460 0 190 690 390 770 640 450 650 190 0 表 2 各景点游览时间 时间 游览时间 开放时间 景点 游客服务中心 阳光草坪 森林小剧场 10-30 分钟 20-60 分钟 30 分钟 9:00-16:00 9:00-17:00 9:00, 9:30, 10:00, 10:30,
    11:00, 11:30, 12:00, 12:30, 13:00, 13:30, 14:00, 14:30, 15:00, 15:30, 16:00, 16:30, 17:00 (半点和整点开放) 儿童科普体验区 儿童戏水场 湿地博物馆 湿地商业街 问题 1 分析： 30-60 分钟 20-60 分钟 30-60 分钟 30 分钟以上 9:00-17:00 9:00-17:00 9:00-17:00 9:00-21:30 二、 问题分析 由题目可知，该题要求在已知两个景点的距离情况下通过一定的路径，固定 起点和终点景点，要求遍历其他六个所有景点。此题作为典型的 TSP 旅行商问题， 加了终点不是起点且固定的条件。在现阶段解决传统的 TSP 问题中，往往会采用 退火算法或者结合遗传算法、蚁群算法等高级算法，但这些算法只在涉及的城市 数量庞大时较为有效，性价比高，因为这些算法并不能得到准确的最优解，只能 得到近似最优解。因此在此题中，固定起点终点仅仅涉及 6 个景点的顺序，一共 720 种可能。我们采用暴力穷举的模型，将每种情况的路径路程长比较得出最短 并输出路径。 问题 2 分析： 游客 12:00 从景石出发，17:00 前到达湿地商业街，17:30 离开湿地商业街 （游览时间最少为 30 分分钟）。设置游览时间最长，路径上损耗时间最短。总时 间控制在 5 个小时以内。由题意可以知道，在路上消耗的时间越短，那么就能尽 可能浏览时间更长。考虑到森林小剧场的开放时间，那么可以依此选择问题一中 的十次次优解，找到符合条件在森林小剧场等待的时间最短的路径情况。 问题 3 分析： 由题意可知，在路上消耗的时间越短，那么就能尽可能浏览时间更长。这就 要求设计为 3 个旅游团分别设计一条最短路径，而且能同时满足游览全部的 7 个
    景点，在一个景点只能容纳 1 个旅游团游览的情况下。由图论的知识可知，这是 在一定约束条件下求最短路径问题，即典型的多旅行商（MTSP)问题。根据图论 的现存的原理求出一个旅行团的最优路线，然后，可将模型改进至 3 个旅行团， 将各个旅行团之间的路线进行目标规划，通过对比分析，可以得出各个旅行团最 优的路径，从而保证旅行过程中总的游览时间最长。 问题 4 分析： 在问题三的模型下，问题四还引入了旅游团的速度和总的等待时间，我们可以 根据由最优路径的定义，从而建立双目标优化模型，即将两个目标都综合起来， 变为一个目标。我们可以假设各旅游团的标准差时间相互独立，由概率论可，多 个随机变量相互独立，多个随机变量和的标准差就等于各自标准差的和。从而把 每个旅行团的标准差时间相加。 三、 模型假设 （1）假设旅游团旅游的过程中没有突发状况的发生 （2）假设当日没有其他时间损失 （3）假设所假设的先后顺序对的 （4）假设各旅游团的期望时间和标准差时间互不影响 四、 符号系统 符号 M A1~A8 C T T1 gL 说明 景区距离的集合 景石和景点①—⑦ 旅游完整个景点的最短距离 在路上的时间 总共在路上耗费的时间 表示地点 i 需要调度服务，且由调度 g 完成该地点的调度任务 这里只列出部分符号
    五、 模型建立 先有统一介绍，对不同的问题分别建模、或根据模型分别讨论。内部可以有 小标题（与摘要相对应）。 5.1 问题 1 的建模与求解 5.1.1 现存模型（蚁群算法） 旅行商问题(Traveling Saleman Problem，TSP)是车辆路径调度问题(VRP)的 特例，由于数学家已证明 TSP 问题是 NP 难题，因此，VRP 也属于 NP 难题。旅 行商问题（TSP）又译为旅行推销员问题、货郎担问题，简称为 TSP 问题，是最 基本的路线问题，该问题是在寻求单一旅行者由起点出发，通过所有给定的需求 点之后，最后再回到原点的最小路径成本[3]。 蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表 明：一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不 能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互 影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的 物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。蚂蚁在运动时能够感 知这种物质,并且习惯于追踪此物质爬行,当然爬行过程中还会释放信息素。一条 路上的信息素踪迹越浓,其它蚂蚁将以越高的概率跟随爬行此路径,从而该路径上 的信息素踪迹会被加强,因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信 息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越 大。蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标 的。我们举例简单说明蚂蚁觅食行为： 如上图 a,b,c 的示意图：
    a 图是原始状态，蚂蚁起始点为 A，要到达 E，中途有障碍物，要绕过才能 到达。BC 和 BH 是绕过障碍物的 2 条路径(假设只有 2 条)。各个路径的距离 d 已经标定。 b 图是 t=0 时刻蚂蚁状态，各个边上有相等的信息素浓度，假设为 15； c 图是 t=1 时刻蚂蚁经过后的状态，各个边的信息素浓度，有变化；因为大 量蚂蚁的选择概率会不一样，而选择概率是和路径长度相关的。所以越短路径的 浓度会越来越大，经过此短路径达到目的地的蚂蚁也会比其他路径多。这样大量 的蚂蚁实践之后就找到了最短路径。所以这个过程本质可以概括为以下几点： 1.路径概率选择机制信息素踪迹越浓的路径,被选中的概率越大 2.信息素更新机制路径越短,路径上的信息素踪迹增长得越快 3.协同工作机制蚂蚁个体通过信息素进行信息交流。 从蚂蚁觅食的原理可见,单个个体的行为非常简单蚂蚁只知道跟踪信息素爬 行并释放信息素,但组合后的群体智能又非常高蚂蚁群能在复杂的地理分布的清 况下,轻松找到蚁穴与食物源之间的最短路径。这种特点恰恰与元启发算法的特 点相一致,蚁群优化算法正是受到这种生态学现象的启发后加以模仿并改进而来, 觅食的蚂蚁由人工蚁替代,蚂蚁释放的信息素变成了人工信息素,蚂蚁爬行和信息 素的蒸发不再是连续不断的,而是在离散的时空中进行。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料