logo资料库

最优化方法案例分析 大学生做的.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：3.51M 资料格式：doc 举报 版权申诉
第1页 / 共82页
第2页 / 共82页
第3页 / 共82页
第4页 / 共82页
第5页 / 共82页
第6页 / 共82页
第7页 / 共82页
第8页 / 共82页
资料共82页，剩余部分请下载后查看
    注意：1.题目自选，每组只选一个 2.选做第二部分案例 8 的小组有加分 3.第一次讨论课定在 4 月 6 号，地点：教七 216 讨论课要求：1.各小组提交报告，报告的写法参照数 学建模课程设计模板 2.各小组组长负责小组内容的报告（PPT 形式），报告完后回答其他小组的提问，小组成员谁 会谁作答 3.每个小组必须在讨论课中提出一个问 题以上，从不提问的小组所有成员讨论课以零分计 运筹学案例(第一部分) 案例 1 高压电器强电流试验计划的安排 某高压电器研究所属行业归口所，是国家高压电器试验检测中心，每年都有 大量的产品试验、中试、出口商检等任务。试验计划安排及实施的过程一般如下： ·提前一个月接受委托试验申请 ·按申请的高压电器类别及台数编制下月计划 ·按计划调度，试验产品进入试验现场 ·试验检测，出检测报告 ·试验完成，撤出现场 高压电器试验分强电流试验和高压电试验两部分，该研究所承担的强电流实 验任务繁重，委托试验的电器量很大，因此科学地计划安排试验计划显得非常重 要。 高压电器分十大类，委托试验的产品有一定随机性，但是试验量最多的产品 （占 85%以上）是以下八类： 1．35KV 断路器
    2．10KV 等级断路器 3．35KV 开关柜 4．10KV 等级开关柜 5．高压熔断器 6．负荷开关 7．隔离开关 8．互感器 这八类产品涉及全国近千个厂家，市场广阔，数量庞大。当前的强电流产品 试验收费标准见表 1-1。 表 1-1 强电流产品试验收费标准 产品类别 试验收费（万元） 1 8 2 6 3 4 5 6 7 8 4 2.5 1 2.2 1.5 1.4 由于强电流试验用的短路发电机启动时,会给城市电网造成冲击,严重影响市 网质量,故只能在中午 1 点用电低谷时启动,从而影响全月连续试验工时只有约 108 小时,任务紧张时只能靠加班调节。正常情况下各种试验所需试验工时见表 8-2。 表 1-2 各类产品试验所需工时 产品类别 试验收费（万元） 1 5 2 4 3 3 4 2 5 2 6 7 8 1.5 1 1.5 强电流试验特点是开机时耗电量大，而每次实验短路时，只持续几秒钟，虽 然短路容量在“0”秒时达 2500 MVA，但瞬时耗电量却很小。每天试验设备提 供耗电量限制为 5000 千瓦，每月 135 千千瓦，那麽每种产品耗量如表 8-3 所示。 各类产品的冷却水由两个日处理能力为 14 吨的冷却塔供给。每月按 27 天计，冷 却水月供给量为 14×27=378 吨。每月各类产品冷却水处理量见表 8-3。 表 1-3 各类产品试验耗电量与冷却水处理量 产品类别 1 2 3 4 5 6 7 耗电量（千瓦） 5000 75000 3000 3000 500 冷却水用量（吨） 10 9 8 8 1 4 2 8 2 600 700 700 根据以往的经验和统计报表显示第一类产品和第二类产品每月最多试验台 数分别为 6 台和 4 台，第三类和第四类产品则每月至少需分别安排 8 台和 10 台。
    根据上述资料，尝试建立数学模型辅助产生排产计划，对模型的优化结果进行解释， 并与实际情况做对比分析。 案例 2.福州市某乡作物种植计划的制定 福州市近郊某乡共有可耕地 2000 亩,其中沙质土地 400 亩,粘质土地 600 亩, 中性土地 1000 亩,主要种植 3 类作物: 第 1 类是以水稻为主的粮食类作物,第 2 类 是蔬菜类,第 3 类是经济作物,以本地特产茉莉花为代表作物。乡政府希望能制定 一个使全乡总收益最大的作物种植计划，据此指导个作业小组和农户安排具体生 产计划。 研究所面临的困难是缺乏历史统计资料及定量数据，只能靠实地调研及与有 经验的老农交谈而获得。因此建立的模型及计算结果只能作为乡政府做决策的参 考，但整个思路和运作过程无疑为科学决策起到了良好的示范作用。 为了简化问题，只考虑水稻、茉莉花作为粮食作物和经济作物的代表，蔬菜 则以当地出产的主要品种为基础测算出每亩的收益及成本的平均值。 每亩土地的费用主要统计和测算外购化肥、劳力工时、灌溉用水及用电等可 以计算的部分，每亩的收益也是根据可能收集到的数据如交公购粮、收购茉莉花
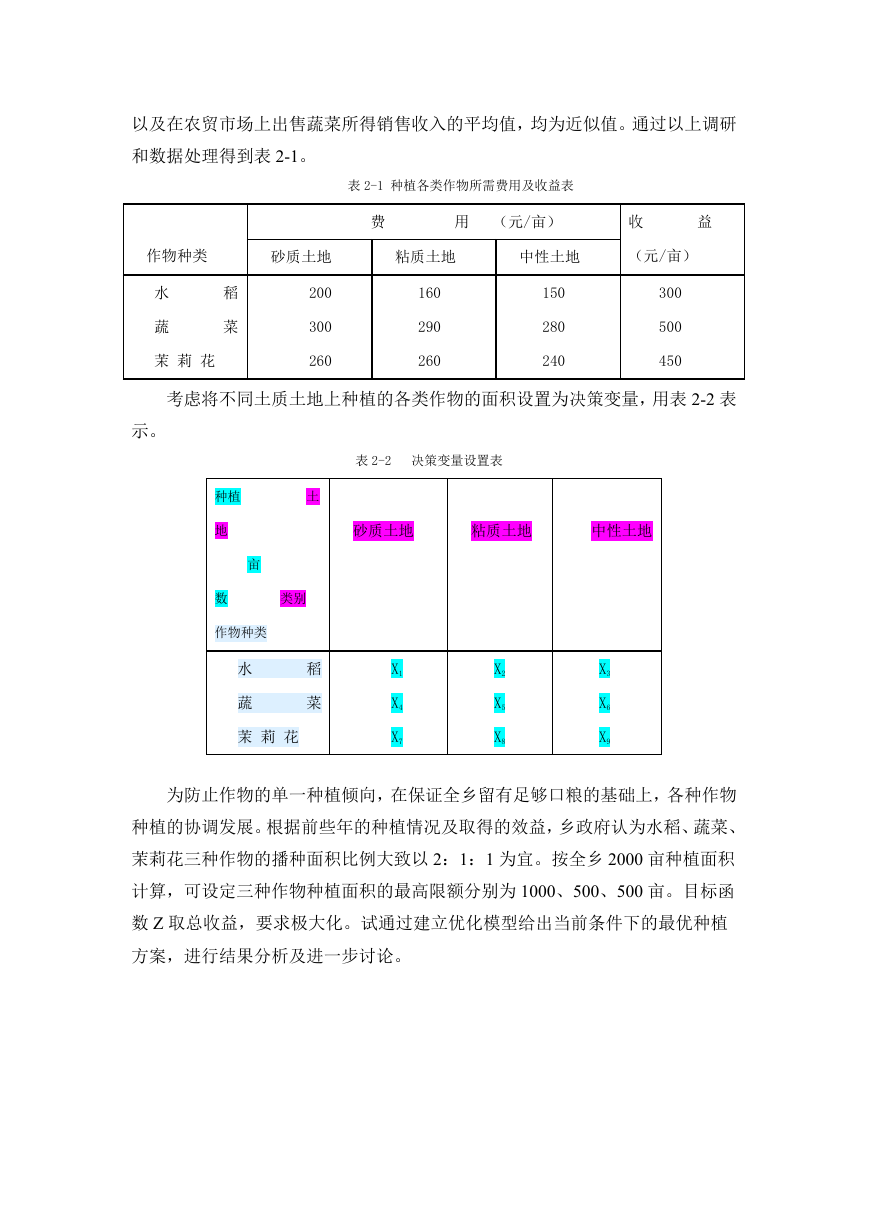
    以及在农贸市场上出售蔬菜所得销售收入的平均值，均为近似值。通过以上调研 和数据处理得到表 2-1。 表 2-1 种植各类作物所需费用及收益表 费 用 （元/亩） 收 益 作物种类 砂质土地 粘质土地 中性土地 （元/亩） 水 蔬 稻 菜 茉 莉 花 200 300 260 160 290 260 150 280 240 300 500 450 考虑将不同土质土地上种植的各类作物的面积设置为决策变量，用表 2-2 表 示。 表 2-2 决策变量设置表 土 稻 菜 种植 地 亩 数 类别 作物种类 水 蔬 茉 莉 花 砂质土地 粘质土地 中性土地 X1 X4 X7 X2 X5 X8 X3 X6 X9 为防止作物的单一种植倾向，在保证全乡留有足够口粮的基础上，各种作物 种植的协调发展。根据前些年的种植情况及取得的效益，乡政府认为水稻、蔬菜、 茉莉花三种作物的播种面积比例大致以 2：1：1 为宜。按全乡 2000 亩种植面积 计算，可设定三种作物种植面积的最高限额分别为 1000、500、500 亩。目标函 数 Z 取总收益，要求极大化。试通过建立优化模型给出当前条件下的最优种植 方案，进行结果分析及进一步讨论。
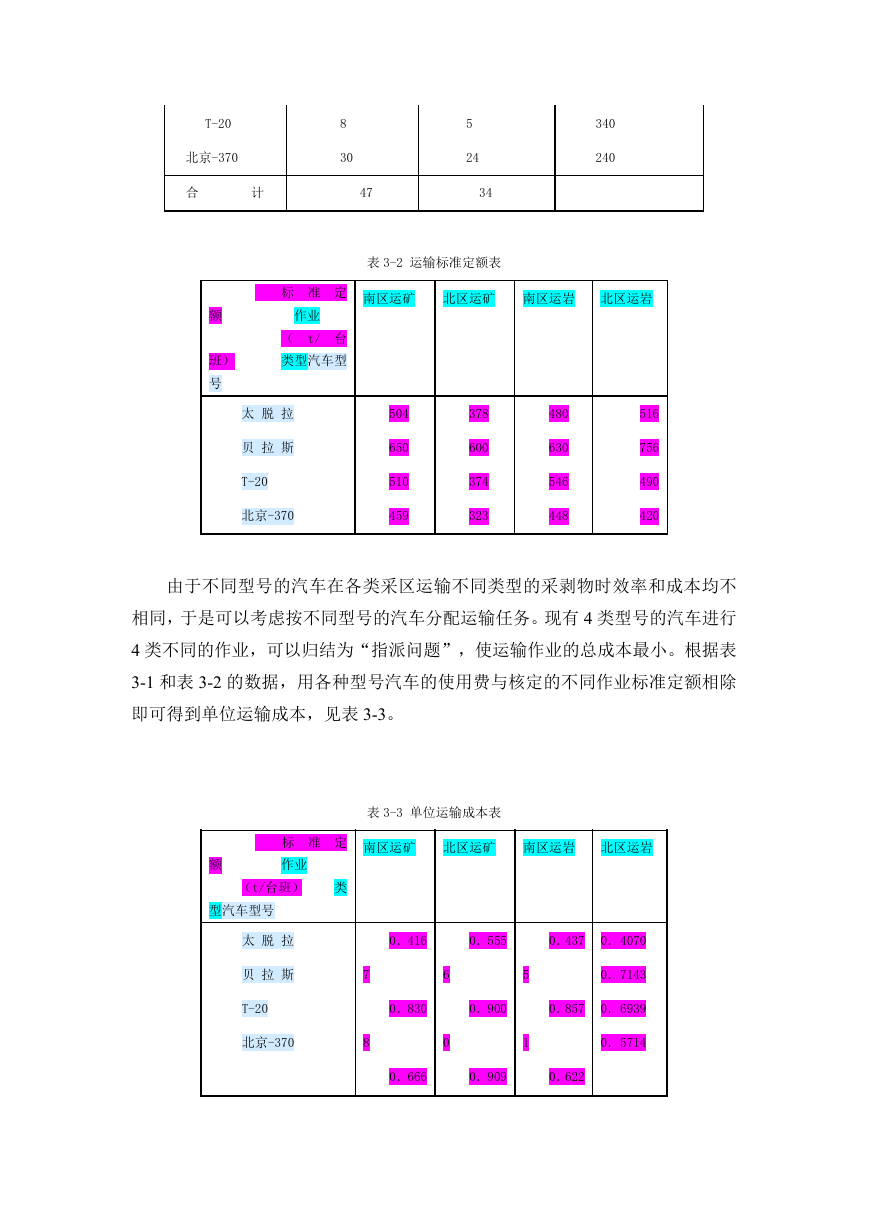
    案例 3 南方某百泥矿合理配车问题的研究 南方某白泥矿是一个南北狭长的露天矿，划分为北区、中区、南区三个开采 区，主要开采生产盆、碗用的白泥，在采矿场附近设有 5 个排土场。 由于开采条件日趋恶化，矿山运输设备效率又不高，人们普遍认为运输问题 已成为影响生产的主要矛盾，希望通过改善管理，挖掘运输潜力，提高经济效益。 全矿共有 4 种型号的运输车辆 34 台，当前的平均单位运费为 0.6490 元/t,运 输车辆的数量和使用费见表 3-1,核定的标准定额见表 3-2。 表 3-1 运输车辆的数量及使用费 汽 车 型 号 在 册 台 数 可 用 台 数 使用费（元/台班） 太 脱 拉 贝 拉 斯 5 4 3 2 210 540
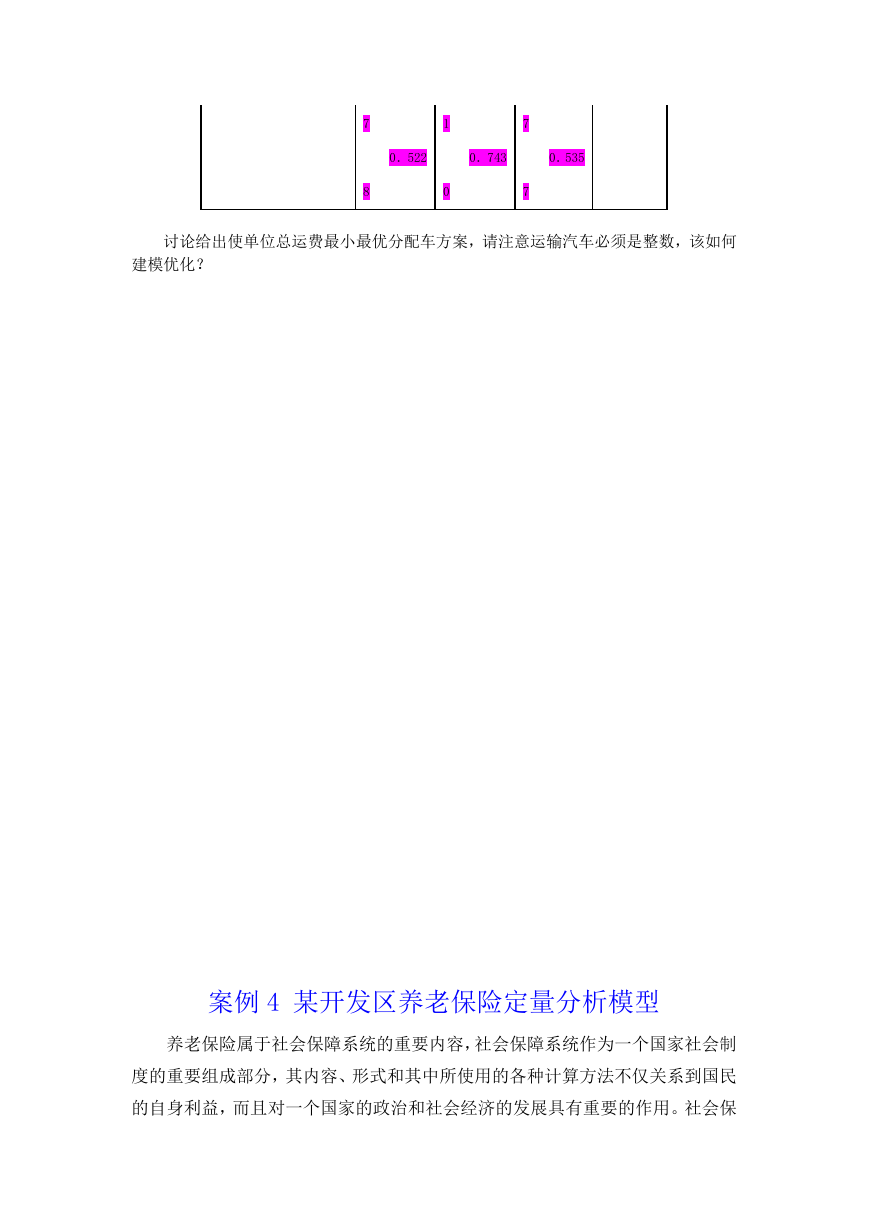
    T-20 北京-370 8 30 合 计 47 5 24 34 340 240 表 3-2 运输标准定额表 标 准 定 南区运矿 北区运矿 南区运岩 北区运岩 额 作业 （ t/ 台 类型汽车型 班） 号 太 脱 拉 贝 拉 斯 T-20 北京-370 504 650 510 459 378 600 374 323 480 630 546 448 516 756 490 420 由于不同型号的汽车在各类采区运输不同类型的采剥物时效率和成本均不 相同，于是可以考虑按不同型号的汽车分配运输任务。现有 4 类型号的汽车进行 4 类不同的作业，可以归结为“指派问题”，使运输作业的总成本最小。根据表 3-1 和表 3-2 的数据，用各种型号汽车的使用费与核定的不同作业标准定额相除 即可得到单位运输成本，见表 3-3。 表 3-3 单位运输成本表 南区运矿 北区运矿 南区运岩 北区运岩 标 准 定 额 作业 （t/台班） 类 型汽车型号 太 脱 拉 贝 拉 斯 T-20 北京-370 0．416 0．555 0．437 0．4070 7 8 0．830 6 0 0．900 5 1 0．7143 0．857 0．6939 0．5714 0．666 0．909 0．622
    7 8 0．522 1 0 0．743 7 7 0．535 讨论给出使单位总运费最小最优分配车方案，请注意运输汽车必须是整数，该如何 建模优化？ 案例 4 某开发区养老保险定量分析模型 养老保险属于社会保障系统的重要内容，社会保障系统作为一个国家社会制 度的重要组成部分，其内容、形式和其中所使用的各种计算方法不仅关系到国民 的自身利益，而且对一个国家的政治和社会经济的发展具有重要的作用。社会保
    障系统中所包含的定量分析和计算是多种多样的，主要包括三个方面：第一，对 社会保障基金提取量的测算；第二，对职工享受社会保障待遇的标准测算；第三， 对社会保障基金各阶段收付额的预测。 基本养老保险金的提取比例一般是一年或若干年调整一次，从数学模型的角 度看两者并无实质性区别，这里定义一年为一个阶段。考虑到养老保险制度是一 个长期制度，具体年限并不确定，因而阶段数可以根据实际问题的研究目标制定。 如：要确定 10 年内各年的提取比例，则阶段数就定为 10；也可以将老龄化程度 最高、养老保险金支付额最大的年份作为决策过程的终止年。不失一般性，将整 个决策过程定义为 n 个阶段。 状态变量 xk 定义为阶段 k 开始时的储备基金，M 是最大储备金额。 决策变量 uk 为阶段 k 基本养老保险金按工资总额提取的比例，这一比例也 应在一定范围之内。按照国际标准，提取比例达到 20%时即为社会预警线，29% 即达到社会承受的极限，因此我们设定 R 为提取的最大比例，若 sk 为阶段 k 的 工资总额，则有： dk-xk≤sk•uk≤min{sk•R,dk+dk+1+…+dn+A-xk} 其中 sk•R 就是基本养老保险金所能提取的最大金额。 已知阶段 k 开始时的储备基金是 xk，阶段 k 的基本养老保险金收入额为 sk• uk ，支付额是 dk。假定储备基金的年增值率为 ik，考虑资金的时间价值，则阶 段末即阶段 k+1 的初始储备基金为： xk+1=（1+ik）xk+sk•uk-dk，即状态转移方程。 可以看出，k+1 阶段的储备基金 xk+1 完全由 k 阶段的储备基金 xk 和基本养老 保险金的提取比例 uk 所决定，与前面的状态和决策无关，即满足无后效性。 设单位资金的管理费用为 L，则阶段 k 的管理费用为：L•sk•uk；设储备基金 的机会损失率为 jk，，则阶段 k 时储备基金的机会损失额为： jk•xk+1=jk[（1+ik）xk+sk•uk-dk]，于是可写出阶段效益的表达式： rk(xk,uk)=L•sk•uk+jk[（1+ik）xk+sk•uk-dk] 目标函数为各阶段效益之和，即 在此基础上，即可写出动态规划基本方程：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料