2019年广东省珠海市中考数学试题.doc-资料库

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

2019 年广东省珠海市中考数学试题说明：1.全卷共 4 页，考试用时 100 分钟，满分为 120 分。 2.答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场等、座位号。用 2 B 钳笔把对应该号码的标号涂黑。 3.选择题毎小题选出答案后，用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上。 4.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答題卡各题目指定区域内相应位置上，如需改动，先划掉原来的答案，然后再写上新的答案：不准使用铅笔和涂改液，不按以上要求作答的答案无效. 5.考生务必保持答题卡的整洁。考试结束时，将试卷和答题卡一并交回。一、选择题（本大题 5 小题，每小题 3 分，共 15 分）在毎小题列出的四个选项中，只有一个是正确的，请把答题卡上对应題目所选的选项涂黑. 1 2  的相反数是（） 1． A．2 1 2 2．边长为 3cm的菱形的周长是（ B． C．-2 ） D．  1 2 A．6cm B．9cm C．12cm D．15cm 3．下列计算中，正确的是（） A．2a+3b=5ab B．（3a3）2=6a6 C．a6+a2=a3 D．-3a+2a=-a 4．已知圆柱体的底面半径为 3cm，髙为 4cm，则圆柱体的侧面积为（） A． 24 cm 2 B． 36 cm 2 C． 12cm 2 D． 24cm 2 5．如图，线段 AB是⊙O的直径，弦 CD丄 AB，∠CAB＝20°，则∠AOD等于（） A．160° B．150° C．140° D．120° 第 5 题图二、填空题（本大题 5 小题，毎小题 4 分，共 20 分）请将下列各题的正确答案填写在答题卡相应的位置上. 6．比较大小：-2 -3（用“＞”、“=”、“＜”填空）。 7．填空， 2 x  4 x 3 (   x  2 )  1 w w w .x k b 1.c o m 8．桶里原有质地均匀、形状大小完全一样的 6 个红球和 4 个白球，小红不慎遗失了其中 2 个红球，现在从桶里随机摸出—个球，则摸到白球的概率为。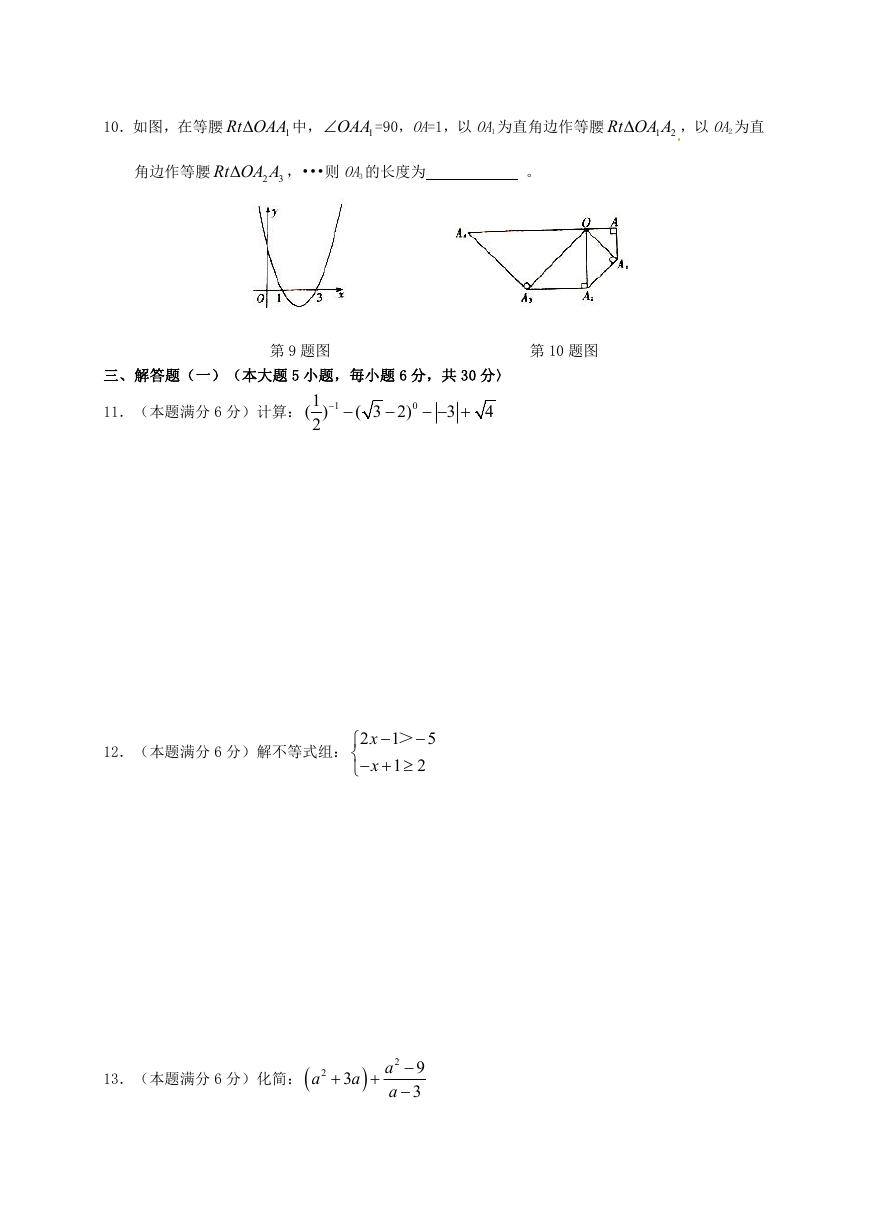 9．如图，对称轴平行于 y 轴的抛物线与 x轴交于（1，0），（3，0）两点，則它的对称轴为。

10．如图，在等腰 Rt OAA 1  中， 1OAA =90，OA=1，以 OA1 为直角边作等腰 Rt OA A 2  1 ，以 OA2 为直角边作等腰 Rt OA A 3  2 ，•••则 OA3 的长度为。第 9 题图第 10 题图三、解答题（一）（本大题 5 小题，毎小题 6 分，共 30 分〉 11．（本题满分 6 分）计算： 1( 2 ) 1   ( 3 2)  0    3 4 12．（本题满分 6 分）解不等式组： 5  1 2   ＞    1 2  x x 13．（本题满分 6 分）化简： 2 a  3 a   2 a a 9  3 

14．（本题满分 6 分）某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目，要求毎位学生必须且只需选考其中一项，该市东风中学初三（2）班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示. （1）求该班的学生人数：（2）若该校初三年级有 1000 人，估计该年级选考立定供远的人数。第 14 题图 xkb1.com 15．（本题满分 6 分）如图，在 Rt ABC （1）用尺规在边 BC上求作一点 P，使 PA=PB（不写作法，保留作图痕迹）中，∠ACB=90°。

（2）连结 AP，当∠B为度时，AP平分∠CAB. 四、解答题（二）（本大题 4 小题，毎小题 7 分，共 28 分〉第 15 题图 16．（本题满分 7 分）为庆祝商都正式营业，商都推出了两种购物方案。方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳 300 元会费成为该商都会员，则所有商品价格可获九折优惠• （1）以 x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中 y关于 x的函数解析式（2）若某人计划在商都购买价格为 5880 元的电视机一台，请分析选择哪种方案更省钱？ 17．（本题满分 7 分）如图，一艘渔船位于小岛Ｍ的北偏东 45°方向、距离小岛 180 海里的 A处，渔船从 A处沿正南方向航行一段距离后，到达位于小岛南偏东 60°方向的 B处。（1）求渔船从 A到 B的航行过程中与小岛 M之间的最小距离（结果用根号表示）：（2）若渔船以 20 海里/小时的速度从 B沿 BM方向行驶，求渔船从 B到达小岛 M的航行时间（结果精确到 0.1 小时）。（参考数据： 2 1.41, 3 1.73, 6    2.45 ）第 17 题图

18．（本题满分 7 分）如图，在 Rt ABC 中，∠BAC=90°，AB=4，AC=3，线段 AB为半圆 O的直径，沿射线 AB方向平移，使斜边与半圆 O相切于点 G，得ΔDEF，DF与 BC交千点 H. 将 Rt ABC （1）求 BE的长：（2）求 Rt ABC 与ΔDEF重叠（阴影）部分的面积。第 18 题图 19．（本题满分 7 分）如图，在平面直角坐标系中，边长为 2 的正方形 ABCD关于 y轴对称，边在 AD在 x轴上，点 B在第四象限，直线 BD与反比例函数 my  的图象交于点 B、E. x （1）求反比例函数及直线 BD的解析式：（2）求点 E的坐标。第 19 题图

五、解答题（三）（本大题 3 小题，毎小题 9 分，共 27 分） 20．（本题满分 9 分）阅读下列材料：解答“已知 x y  ，且 1, x y＞＜，试确定 x 2 0 y 的取值范围”有如下解法：解  x   y 2,    x y 2 、又  x ＞ 1, y  2 1. ＞ y ＞- 1. 又 0,  ＜ y 同理得： 1  ＜＜。 …………① 0 y 由①+②得 -1 1  1 x＜＜2 。 …………②、 y 0 2  ＜＜  x y  的取值范围是 0 x 2 y＜＜ x 请按照上述方法，完成下列问题：（1）已知 x y  ，且 3 x y＞2 ＜1，则 x , y 的取值范围是 .   成立，求 x a y y 的取值范围（结果用含 a的式子表示）。（2）已知 y x＞1 ＜-1 ，若 x , xk|b|1

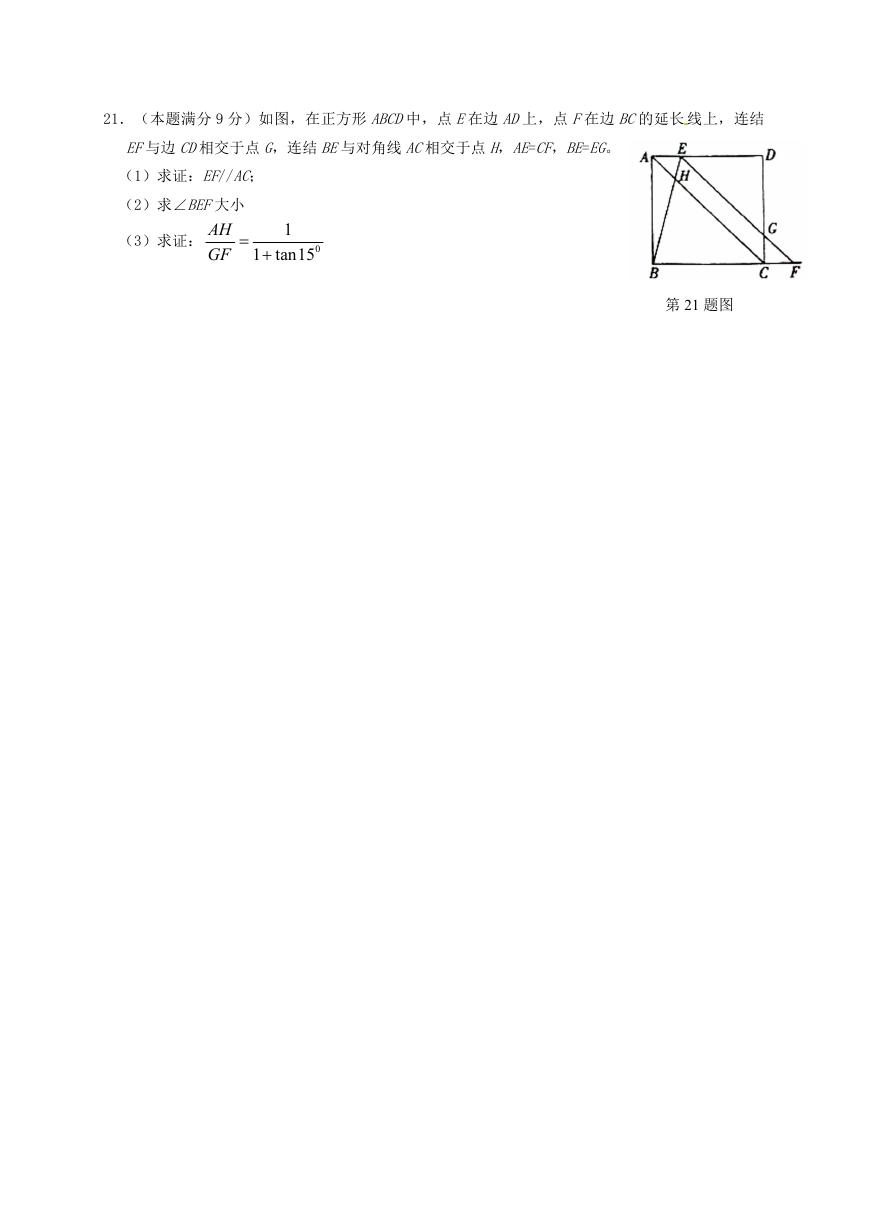
21．（本题满分 9 分）如图，在正方形 ABCD中，点 E在边 AD上，点 F在边 BC的延长线上，连结 EF与边 CD相交于点 G，连结 BE与对角线 AC相交于点 H，AE=CF，BE=EG。（1）求证：EF//AC；（2）求∠BEF大小（3）求证： AH GF  1 1 tan15  0 第 21 题图 [来源:学,科,网] w w w .x k b 1.c o m

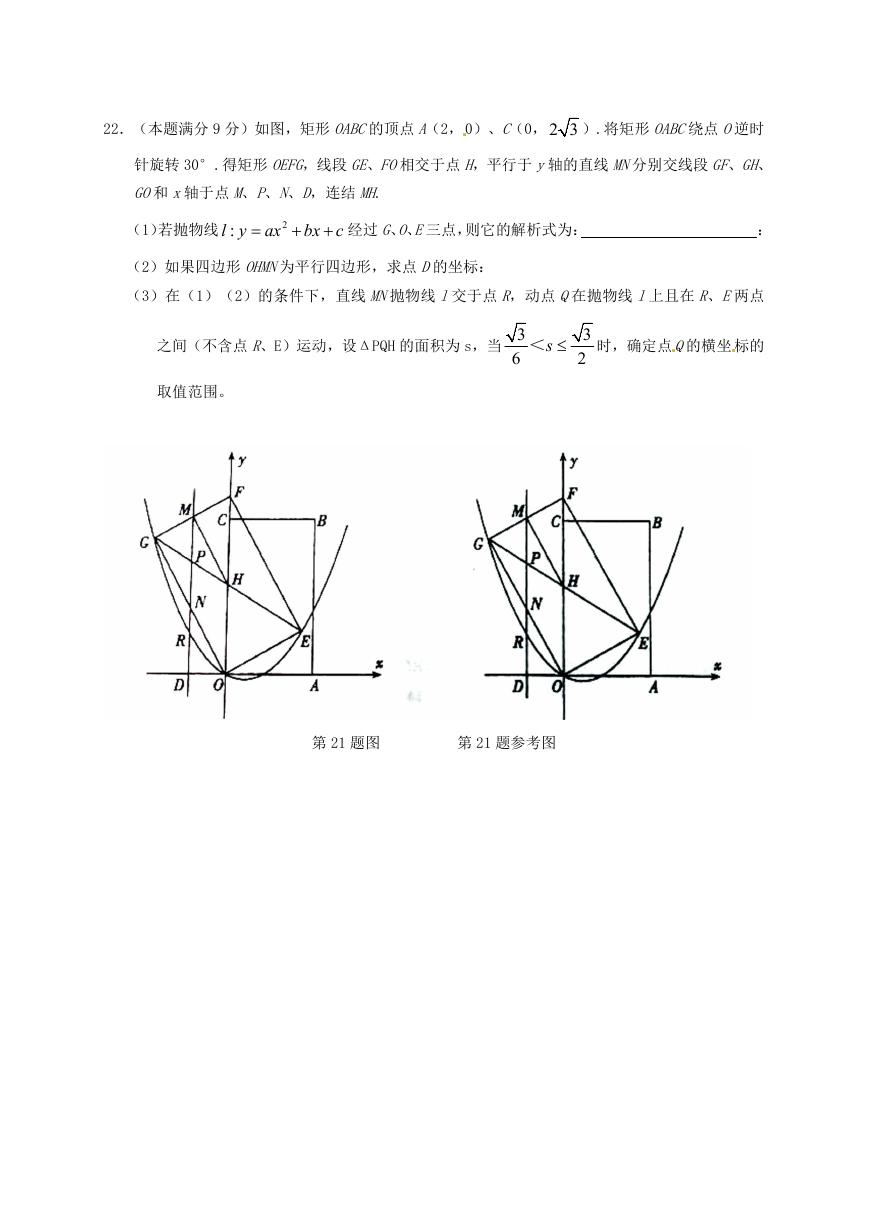
22．（本题满分 9 分）如图，矩形 OABC的顶点 A（2， 0）、C（0，2 3 ）.将矩形 OABC绕点 O逆时针旋转 30°.得矩形 OEFG，线段 GE、FO相交于点 H，平行于 y轴的直线 MN分别交线段 GF、GH、 GO和 x轴于点 M、P、N、D，连结 MH. （1）若抛物线 :l y  2 ax  bx  经过 G、O、E三点，则它的解析式为： c ：（2）如果四边形 OHMN为平行四边形，求点 D的坐标：（3）在（1）（2）的条件下，直线 MN抛物线 l交于点 R，动点 Q在抛物线 l上且在 R、E两点之间（不含点 R、E）运动，设ΔPQH 的面积为 s，当 3 6 s ＜ 3 2 时，确定点 Q的横坐标的取值范围。第 21 题图第 21 题参考图

资料库

2019年广东省珠海市中考数学试题.doc

相关推荐

中考

热门标签

最新资料