2018下半年教师资格考试初中数学面试真题.doc

发布时间：2022-09-07 发布人：admin 分类：说明书资料大小：1.62M 资料格式：doc 举报版权申诉

第1页 / 共30页

第2页 / 共30页

第3页 / 共30页

第4页 / 共30页

第5页 / 共30页

第6页 / 共30页

第7页 / 共30页

第8页 / 共30页

《多项式》

《有理数的乘方》

《行四边形的判定》

《轴对称现象》

《勾股定理》

2018 下半年教师资格考试初中数学面试真题《菱形的判定》一、试讲题目 1.题目：菱形的判定 2.内容： 3.基本要求 (1)试讲时间 10 分钟左右; (2)讲解要目的明确、条理清楚、重点突出; (3)讲解证思路,说明理根据,反思证时过程; (4)根据讲解的需要适当板书。【试题解析析】

《菱形的判定》学段:初中课型:新授课课时:1 课时教学过程：一、复习导入师:上课之前老师先带着大家一起复习一下之前学习过的萎形的定义和性质。(引导学生进行回顾) 生:一组临边相等的平行四边形是菱形。生:菱形的两组对边分别平行,四条边都相等;菱形具有平行四边形的所有性质。教师揭示课题:那么我们定一个平行四边形是否为菱形,除了用定义判定以外,还有没有别的方法?今天我们就一起来探究一下《菱形的判定》二、探究新知 (一)动手操作,实验探究师:请同学们拿出课前老师让大家准备的木条和钉子,将这两根木条的中心用钉子固定起来, 做成一个可以转动的十字架,然后周围围上一根橡皮筋,做成一个平行四边形。学生操作,教师巡视。巡视过程提醒学生注意安全操作。师:任意转动木条,大家发现这个四边形有什么特征,你的能证明你的结论吗? 师:继续转动木条,观察什么时候橡皮筋会围城萎形,如何去证明这个猜想?

生:对角线互相垂直的平行四边形是菱形。(猜想) 师:那这个命题的前提是什么? (二)几何证明,得出方法师:接下来同学们用几何语言描述这个命题。生:在◇ABCD 中,对角线 AC⊥BD，求证◇ABCD 是菱形。师:我们应该依据什么来证明呢? 生:可以依据菱形的定义来证明。生:由平行四边形的性质得到 BO=DO,由∠AOB=∠AOD=90°及 AO=AO,得 △ AOB≌△AOD，进而得到 AB=AD,最后得出◇ABCD 是菱形。 (三)归纳结论,形成判定定理通过探究和进一步证明可以归纳得到菱形的第二个判定方法:对角线互相垂直的平行四边形是菱形。三、巩因练习用课件例题,并让学生完成例题。四、课堂小结教师引导学生谈谈这节课学习的收获。

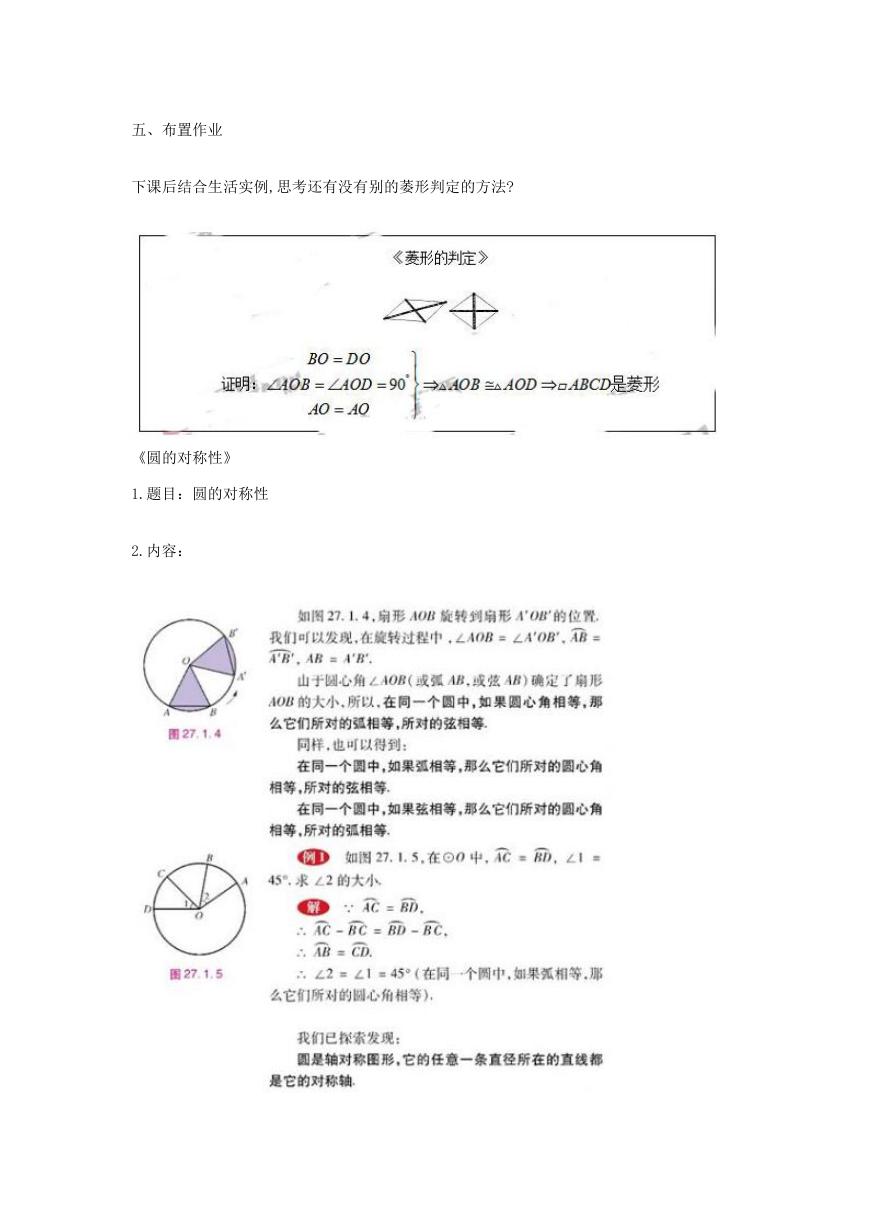
五、布置作业下课后结合生活实例,思考还有没有别的萎形判定的方法? 《圆的对称性》 1.题目：圆的对称性 2.内容：

3.基本要求：（1）试讲时间 10 分钟左右；（2）讲解要目的明确、条理清楚、重点突出；（3）根据讲解的需要适当板书和作图；（4）学生掌握圆的对称性；答辩题目：1.什么是对称图形？圆的对称轴有多少条？ 2.垂径定理的什么？二、考题解析【教学过程】 (一)引入新课教师引导学生在纸上画两个大小相同的圆，然后将其剪下来，引导学生思考：将两个圆放在一起会怎么样?若将其中一个转动，两个圆是否还会重合?通过这两个问题让学生认识到圆是旋转的对称图形，进一步提问：对称中心是什么?进一步引导学生思考与圆的对称性有关的性质有哪些?引出课题。 (二)探索新知对于导入中的问题，教师引导学生画两个完全相同的圆，然后将其中的一个圆剪下一个扇形 AOB，引导学生将扇形 AOB 放在另外一个圆上，将顶点放在圆心上，画出扇形 AOB，然后再引导学生将其旋转，再画出扇形 A'OB'，观察前后两个扇形，并思考：这两个扇形的中的圆心角、弦、弧有什么样的关系? 预设：两个扇形是完全相同的。

提问：扇形的大小由什么确定? 预设：扇形的大小由圆心角确定。提问：能否用一句话说说上述的发现。预设：如果圆心角相等，那么它们所对的弧相等，所对的弦相等。进一步提问：在同一个圆呢?还是在两个圆中?若在两个圆中存在，这两个圆是什么关系。师生共同总结得出：在等圆和同一个圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等。提问：能否说说上述结论中的条件和结论。预设：条件是在同圆或等圆中，圆心角相同，结论是：①所对的弧相等，②所对的弦相等。引导学生思考：如果互换条件和结论，那命题是否还正确? 预设 1：在同圆或等圆中，所对的弧相等，那么它们所对的圆心角相等，所对的弦也相等。预设 2：在同圆或等圆中，所对的弦相等，那么它们所对的圆心角相等，所对的弧也相等。最后师生共同得出：在同圆或等圆中，已知三个量中的其中一个量相等，就可以得出另外两个量也相等。组织学生进行动手操作，折一折，说说圆是什么样的图形?进一步提问它的对称轴是什么? 对称轴有多少条? 最后师生共同得出：圆是对称图形，它的任意一条直径所在的直线都是它的对称轴。引导学生思考：怎样将圆平均分成 2 等分，4 等分、8 等分?进一步提问还可以将圆平均分成多少等分?

最后师生共同得到：将圆沿直径对折平均分成 2 等分，再对折一次，平均成 4 等分，再对折就可以将圆平均分成 8 等分，再对折，就可以平均分成 16 等分了，再对折 32 等分等等。 (三)课堂练习例 1 (四)小结作业提问：今天有什么收获? 课后作业：思考当直径与弦垂直时，那所对的弧有什么关系? 【板书设计】略《平行线的性质》 1.题目：平行线的性质 2.内容：

3.基本要求：（1）有板书设计；（2）学生能够总结归纳出平行线的性质，并且应用性质判断角的关系；（3）教学中注意条理清晰，重点突出；（4）请在 10 分钟内完成试讲内容。答辩题目：1.随便说出 4 个教学中的基本事实。 2.如何检验学生对于知识的掌握？

分享到：

赞收藏

资料库

2018下半年教师资格考试初中数学面试真题.doc

相关推荐

教师资格考试

热门标签

最新资料