CPM算法（Uncovering_the_overlapping_community....pdf

发布时间：2022-06-01 发布人：admin 分类：说明书资料大小：0.54M 资料格式：pdf 举报版权申诉

ls03101409-6924225-4744302542943189799.pdf-第1页.png

第1页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第2页.png

第2页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第3页.png

第3页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第4页.png

第4页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第5页.png

第5页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第6页.png

第6页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第7页.png

第7页 / 共10页

ls03101409-6924225-4744302542943189799.pdf-第8页.png

第8页 / 共10页

文本预览

Uncovering the overlapping community structure of complex networks in nature and society 5 0 0 2 n u J 5 1 ] h p - c o s . s c i s y h p [ 1 v 3 3 1 6 0 5 0 / s c i s y h p : v i X r a Gergely Palla†‡, Imre Der´enyi‡, Ill´es Farkas†, and Tam´as Vicsek†‡ †Biological Physics Research Group of HAS, P´azm´any P. stny. 1A, H-1117 Budapest, Hungary, ‡Dept. of Biological Physics, E¨otv¨os University, P´azm´any P. stny. 1A, H-1117 Budapest, Hungary. Many complex systems in nature and society can be described in terms of networks capturing the intricate web of connections among the units they are made of [1, 2, 3, 4]. A question of interest is how to interpret the global organisation of such networks as the coexistence of their structural sub-units (communities) associated with more highly interconnected parts. Identifying these a pri- ori unknown building blocks (functionally related proteins [5, 6], industrial sectors [7], groups of people [8, 9], etc.) is crucial to the understanding of the structural and functional properties of networks. The existing deterministic methods used for large networks ﬁnd separated communi- ties, while most of the actual networks are made of highly overlapping cohesive groups of nodes. Here we introduce an approach to analyse the main statistical features of the interwoven sets of overlapping communities making a step towards the uncovering of the modular structure of com- plex systems. After deﬁning a set of new characteristic quantities for the statistics of communities, we apply an efﬁcient technique to explore overlapping communities on a large scale. We ﬁnd that overlaps are signiﬁcant, and the distributions we introduce reveal universal features of networks. Our studies of collaboration, word association, and protein interaction graphs demonstrate that the web of communities has non-trivial correlations and speciﬁc scaling properties. Most real networks typically contain parts in which the nodes (units) are more highly connected to each other than to the rest of the network. The sets of such nodes are usually called clusters, communities, cohesive groups, or modules [8, 10, 11, 12, 13], having no widely accepted, unique deﬁnition. In spite of this ambiguity the presence of communities in networks is a signature of the hierarchical nature of complex systems [5, 14]. The existing methods for ﬁnding communities in large networks are useful if the community structure is such that it can be interpreted in terms of separated sets of communities (see Fig. 1b and Refs. [10, 15, 16, 17, 18]). However, most real networks are characterised by well deﬁned statistics of overlapping and nested communities. Such a statement can be demonstrated by the numerous communities each of us belongs to, including those related to our scientiﬁc activities or personal life (school, hobby, family) and so on, as illustrated in Fig. 1a. Furthermore, members of our communities have their own communities, resulting in an extremely complicated web of the communities themselves. This has long been appreciated by sociologists [19], but has never been studied systematically for large networks. Another, biological example is that a large fraction of proteins belong to several protein complexes simultaneously [20]. In general, each node i of a network can be characterised by a membership number mi, which is the number of communities the node belongs to. In turn, any two communities α and β can share sov α,β nodes, which we deﬁne as the overlap size between these communities. Naturally, the communities also constitute a network with the overlaps being their links. The number of such links of community 1

a) Scientists Mathematicians Physicists Department of Biological Physics Biologists "zoom" "zoom" Hobby Scientific Community Family Friends Schoolmates c) b) all people Includes colleagues, friends, schoolmates, family members, etc. Figure 1: Illustration of the concept of overlapping communities. a) The black dot in the middle rep- resents either of the authors of this Letter, with several of his communities around. Zooming into the scientiﬁc community demonstrates the nested and overlapping structure of the communities, while de- picting the cascades of communities starting from some members exempliﬁes the interwoven structure of the network of communities. b) Divisive and agglomerative methods grossly fail to identify the com- munities when overlaps are signiﬁcant. c) An example of overlapping k-clique-communities at k = 4. The yellow community overlaps with the blue one in a single node, whereas it shares two nodes and a link with the green one. These overlapping regions are emphasised in red. Notice that any k-clique (complete subgraph of size k) can be reached only from the k-cliques of the same community through a series of adjacent k-cliques. Two k-cliques are adjacent if they share k − 1 nodes. α . Finally, the size scom of any community α can most α can be called as its community degree, dcom naturally be deﬁned as the number of its nodes. To characterise the community structure of a large network we introduce the distributions of these four basic quantities. In particular, we will focus on their cumulative distribution functions denoted by P (scom), P (dcom), P (sov), and P (m), respectively. For the overlap size, e.g., P (sov) means the proportion of those overlaps that are larger than sov. Further relevant statistical features will be introduced later. α The basic observation on which our community deﬁnition relies is that a typical community consists of several complete (fully connected) subgraphs that tend to share many of their nodes. Thus, we deﬁne a community, or more precisely, a k-clique-community as a union of all k-cliques (complete subgraphs of size k) that can be reached from each other through a series of adjacent k-cliques (where adjacency means sharing k − 1 nodes) [21, 23, 24]. This deﬁnition is aimed at representing the fact that it is an essential feature of a community that its members can be reached through well connected subsets of nodes. There are other parts of the whole network that are not reachable from a particular k-clique, but they potentially contain further k-clique-communities. In turn, a single node can belong to several communities. All these can be explored systematically and can result in a large number of overlapping communities (see 2

Fig. 1c for illustration). Note that in most cases relaxing this deﬁnition (e.g., by allowing incomplete k-cliques) is practically equivalent to lowering the value of k. For ﬁnding meaningful communities, the way they are identiﬁed is expected to satisfy several basic requirements: it cannot be too restrictive, should be based on the density of links, is required to be local, should not yield any cut-node or cut- link (whose removal would disjoin the community) and, of course, should allow overlaps. We employ the community deﬁnition speciﬁed above, because none of the others in the literature satisfy all these requirements simultaneously [21, 22]. Although the numerical determination of the full set of k-clique-communities is a polynomial prob- lem, we use an algorithm which is exponential, because it is signiﬁcantly more efﬁcient for the graphs corresponding to actual data. This method is based on ﬁrst locating all cliques (maximal complete subgraphs) of the network and then identifying the communities by carrying out a standard component analysis of the clique-clique overlap matrix [21]. For more details about the method and its speed see the Supplementary Information. We use our method for binary networks (i.e., with undirected and unweighted links). An arbitrary network can always be transformed into a binary one by ignoring any directionality in the links and keeping only those that are stronger than a threshold weight w∗. Changing the threshold is like changing the resolution (as in a microscope) with which the community structure is investigated: by increasing w∗ the communities start to shrink and fall apart. A very similar effect can be observed by changing the value of k as well: increasing k makes the communities smaller and more disintegrated, but at the same time, also more cohesive. When we are interested in the community structure around a particular node, it is advisable to scan through some ranges of k and w∗, and monitor how its communities change. As an illustration, in Fig. 2 we are depicting the communities of three selected nodes of three large networks: (i) the social network of scientiﬁc collaborators [25], (ii) the network of word associations [26] related to cognitive sciences, and (iii) the molecular-biological network of protein-protein interactions [27]. These pictures can serve as tests or validations of the efﬁciency of our algorithm. In particular, the communities of the author G. Parisi (who is well known to have been making signiﬁcant contributions in different ﬁelds of physics) shown in Fig. 2a are associated with his ﬁelds of interest, as it can be deduced from the titles of the papers involved. The 4-clique-communities of the word “bright” (Fig. 2b) correspond to the various meanings of this word. An important biological application is ﬁnding the communities of proteins, based on their interactions. Indeed, most proteins in the communities shown in Figs. 2c and 3 can be associated with either protein complexes or certain functions, as can be looked up by using the GO-TermFinder package [28] and the online tools of the Saccharomyces Genome Database (SGD) [29]. For some proteins no function is available yet. Thus, the fact that they show up in our approach as members of communities can be interpreted as a prediction for their functions. One such example can be seen in the enlarged portion of Fig. 3. For the protein Ycr072c, which is required for the viability of the cell and appears in the dark green community on the right, SGD provides no biological process (function). By far the most signiﬁcant GO term for the biological process of this community is “ribosome biogenesis/assembly”. Thus, we can infer that Ycr072c is likely to be involved in this process. Also, new cellular processes can be predicted if yet unknown communities are found with our method. These examples (and further ones included in the Supplementary Information) clearly demonstrate the advantages of our approach over the existing divisive and agglomerative methods recently used for large real networks. Divisive methods cut the network into smaller and smaller pieces, each node is 3

Figure 2: The community structure around a particular node in three different networks. The commu- nities are colour coded, the overlapping nodes and links between them are emphasised in red, and the volume of the balls and the width of the links are proportional to the total number of communities they belong to. For each network the value of k has been set to 4. a) The communities of G. Parisi in the co-authorship network of the Los Alamos cond-mat archive (for threshold weight w∗ = 0.75) can be associated with his ﬁelds of interest. b) The communities of the word “bright” in the South Florida Free Association norms list (for w∗ = 0.025) represent the different meanings of this word. c) The commu- nities of the protein ZDS1 in the DIP core list of the protein-protein interactions of S. cerevisiae can be associated with either protein complexes or certain functions. forced to remain in only one community and be separated from its other communities, most of which then necessarily fall apart and disappear. This happens, e.g., with the word “bright” when we apply the method described in Ref. [16]: it tends to stay together mostly with the words of the community related to “light”, while most of its other communities (e.g., those related to “colors”, see Fig. 2b) completely disintegrate (“green” gets to the vegetables, “orange” to the fruits, etc.). Agglomerative methods do the same, but in the reverse direction. For example, when we applied the agglomerative method of Ref. [18], at some point “bright”, as a single word, joined a “community” of 890 other words. In addition, such methods inevitably lead to a tree-like hierarchical rendering of the communities, while our approach allows the construction of an unconstrained network of communities. The networks chosen above have been constructed in the following ways. In the co-authorship net- 4

work of the Los Alamos e-print archives [25] each article contributes the value 1/(n − 1) to the weight of the link between every pair of its n authors. In the South Florida Free Association norms list [26] the weight of a directed link from one word to another indicates the frequency that the people in the survey associated the end point of the link with its start point. For our purposes these directed links have been replaced by undirected ones with a weight equal to the sum of the weights of the corresponding two oppositely directed links. In the DIP core list of the protein-protein interactions of S. cerevisiae [27] each interaction represents an unweighted link between the interacting proteins. These networks are very large, consisting of 30739, 10617, and 2609 nodes and 136065, 63788, and 6355 links, respectively. Although different values of k and w∗ might be optimal for the local community structure around different nodes, we should set some global criterion to ﬁx their values if we want to analyse the statistical properties of the community structure of the entire network. The criterion we use is based on ﬁnding a community structure as highly structured as possible. In the related percolation phenomena [24] a giant component appears when the number of links is increased above some critical point. Therefore, to approach this critical point from below, for each selected value of k (typically between 3 and 6) we lower the threshold w∗ until the largest community becomes twice as big as the second largest one. In this way we ensure that we ﬁnd as many communities as possible, without the negative effect of having a giant community that would smear out the details of the community structure by merging many smaller communities. We denote by f ∗ the fraction of links stronger than w∗, and use only those values of k for which f ∗ is not too small (not smaller than 0.5). This has led us to k = 6 and 5 with f ∗ = 0.93 and 0.75, respectively, for the collaboration network, and k = 4 with f ∗ = 0.67 for the word association network. For the former network both sets of parameters result in very similar communities (see the Supplementary Information). Since for unweighted networks no threshold weight can be set, for these we simply select the smallest value of k for which no giant community appears. In case of the protein interaction network this gives k = 4, resulting in 82 communities. Due to this relatively low number, we can depict the entire network of protein communities as presented in Fig. 3. 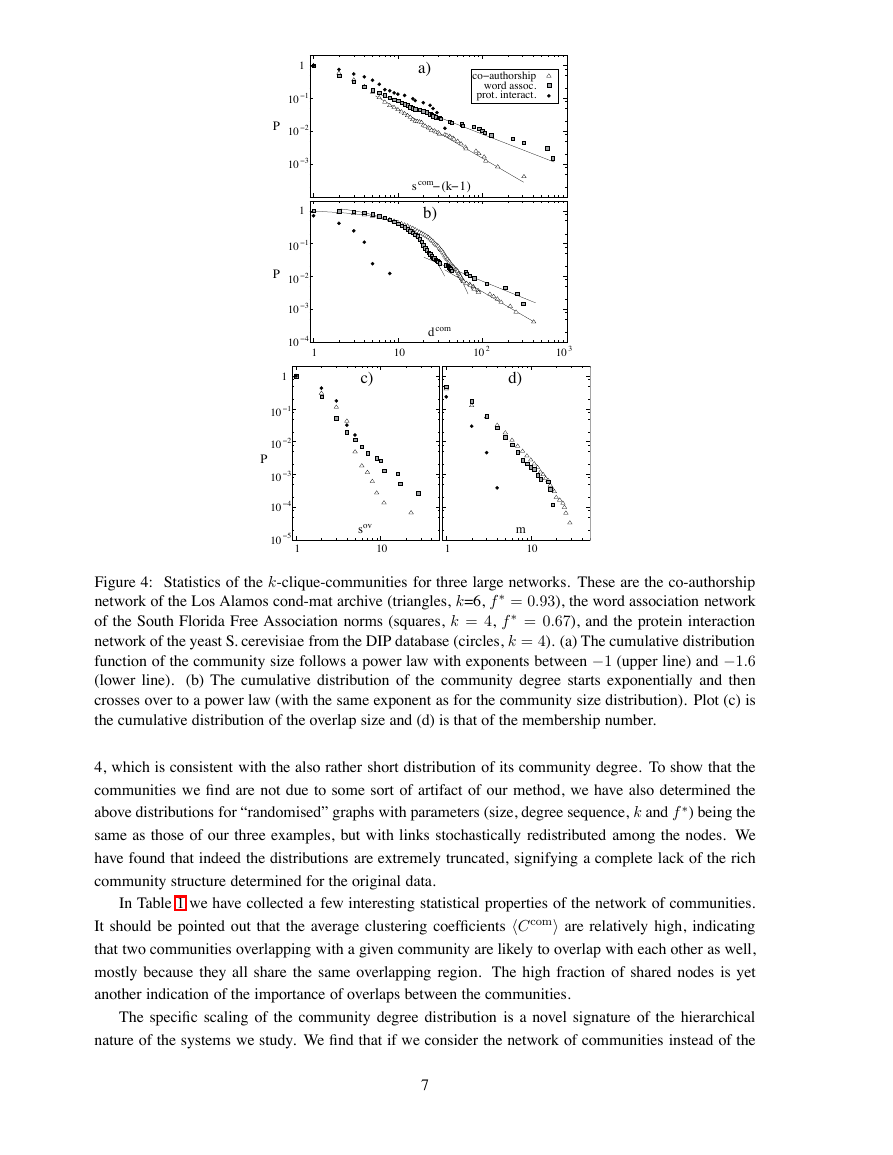The four distributions characterising the global community structure of these networks are displayed in Fig. 4. Although the scaling of the size of non-overlapping communities has already been demon- strated for social networks [18, 17], it is striking to observe how this aspect of large real networks is preserved even when a more complete picture (allowing overlaps) is investigated. In Fig. 4a the power law dependence P (scom) ∼ (scom)−τ with an exponent ranging between τ = 1 and 1.6 is well pro- nounced and is valid nearly over the entire range of community sizes. ) with a characteristic community degree dcom It is well known [2, 3, 4] that the nodes of large real networks have a power law degree distri- bution. Will the same kind of distribution hold when we move to the next level of organisation and consider the degrees of the communities? Remarkably, we ﬁnd that it is not the case. The community degrees (Fig. 4b) have a very unique distribution, consisting of two distinct parts: an exponential decay (which is in the order of P (dcom) ∼ exp(−dcom/dcom hdcomi shown in Table 1), followed by a power law tail ∼ (dcom)−τ . This new kind of behaviour is consistent with the community size distribution assuming that on average each node of a community has a contribution δ to the community degree. The tail of the community degree distribution is, therefore, simply proportional to that of the community size distribution. At the ﬁrst part of P (dcom), on the other hand, a characteristic scale dcom 0 ∼ kδ appears, because the majority of the communities have a size of the order of k (see Fig. 4a) and their distribution around dcom dominates this part of the curve. Thus, the degree to which P (dcom) deviates from a simple scaling depends on k or, in other words, on the 0 0 0 5

43S complex and protein metabolism Prt1 Cka2 Cdc68 CK2 complex and transcription regulation Ckb1 Protein phosphatase type 2A complex (part) Abf1 Arp4 Hht1 Rts3 Tpd3 Sir4 Cdc55 Pph21 Pph22 Zds2 Gic2 Hst1 Hos2 Sif2 Snt1 Cph1 Set3c complex Zds1 Hos4 Bob1 Set3 Ste20 Bem1 Cdc24 Hcr1 Sui1 Tif34 Tif35 Ckb2 Sua7 Tif5 Rpg1 Tif6 Ribosome biogenesis/assembly Nop7 Nog2 Mak11 Rpf2 Dbp10 Ytm1 Puf6 Bud20 Nsa2 Arx1 Rlp7 Nop15 Nug1 Ycr072c Has1 Erb1 Cka1 Nop12 Mak21 Brx1 Mak5 Sda1 Nop2 Cic1 Hta1 Nop4 Nop6 Htb1 DNA packaging, Mdn1 Rrp12 chromatin assembly Hhf1 Sir3 Chromatin silencing Sir1 Rrp14 Cell polarity, Cla4 budding Cdc12 Bni5 Gic1 Rga1 Cdc42 Cdc11 Gin4 Shs1 Kcc4 Far1 Pheromone response (cellular fusion) Cdc10 Cdc3 Cytokinesis (septin ring) Figure 3: Network of the 82 communities in the DIP core list of the protein-protein interactions of S. cerevisiae for k = 4. The area of the circles and the width of the links are proportional to the size of the corresponding communities (scom α,β), respectively. The coloured communities are cut out and magniﬁed to reveal their internal structure. In this magniﬁed picture the nodes and links of the original network have the same colour as their communities, those that are shared by more than one community are emphasised in red, and the grey links are not part of these communities. The area of the circles and the width of the links are proportional to the total number of communities they belong to. α ) and to the size of the overlaps (sov prescribed minimum cohesiveness of the communities. The extent to which different communities overlap is also a relevant property of a network. Although the range of overlap sizes is limited, the behaviour of the cumulative overlap size distribution P (sov), shown in Fig. 4c, is close to a power law for each network, with a rather large exponent. We can conclude that there is no characteristic overlap size in the networks. Finally, in Fig. 4d we display the cumulative distribution of the membership number, P (m). These plots demonstrate that a node may belong to a number of communities. In the collaboration and the word association network there seems to be no characteristic value for the membership number: the data are close to a power law dependence, with a large exponent. In the protein interaction network, however, the largest membership number is only 6

1 10 −1 P 10 −2 10 −3 1 10 −1 P 10 −2 10 −3 10 −4 1 1 10 −1 10 −2 10 −3 10 −4 P 10 −5 1 a) co−authorship word assoc. prot. interact. com 1 s −(k− ) b) d com 10 10 2 10 3 c) d) sov 10 1 m 10 Figure 4: Statistics of the k-clique-communities for three large networks. These are the co-authorship network of the Los Alamos cond-mat archive (triangles, k=6, f ∗ = 0.93), the word association network of the South Florida Free Association norms (squares, k = 4, f ∗ = 0.67), and the protein interaction network of the yeast S. cerevisiae from the DIP database (circles, k = 4). (a) The cumulative distribution function of the community size follows a power law with exponents between −1 (upper line) and −1.6 (lower line). (b) The cumulative distribution of the community degree starts exponentially and then crosses over to a power law (with the same exponent as for the community size distribution). Plot (c) is the cumulative distribution of the overlap size and (d) is that of the membership number. 4, which is consistent with the also rather short distribution of its community degree. To show that the communities we ﬁnd are not due to some sort of artifact of our method, we have also determined the above distributions for “randomised” graphs with parameters (size, degree sequence, k and f ∗) being the same as those of our three examples, but with links stochastically redistributed among the nodes. We have found that indeed the distributions are extremely truncated, signifying a complete lack of the rich community structure determined for the original data. In Table 1 we have collected a few interesting statistical properties of the network of communities. It should be pointed out that the average clustering coefﬁcients hC comi are relatively high, indicating that two communities overlapping with a given community are likely to overlap with each other as well, mostly because they all share the same overlapping region. The high fraction of shared nodes is yet another indication of the importance of overlaps between the communities. The speciﬁc scaling of the community degree distribution is a novel signature of the hierarchical nature of the systems we study. We ﬁnd that if we consider the network of communities instead of the 7

co-authorship word assoc. prot. interact. N com hdcomi 12.10 2450 11.33 670 82 1.54 hC comi 0.44 0.56 0.17 hri 58% 72% 26% Table 1: Statistical properties of the network of communities. N com is the number of communities, hdcomi is the average community degree, hC comi is the average clustering coefﬁcient of the network of communities, and hri represents the average fraction of shared nodes in the communities. nodes themselves, we still observe a degree distribution with a fat tail, but a characteristic scale appears, below which the distribution is exponential. This is consistent with our understanding of a complex system having different levels of organisation with units speciﬁc to each level. In the present case the principle of organisation (scaling) is preserved (with some speciﬁc modiﬁcations) when going to the next level in good agreement with the recent ﬁnding of the self-similarity of many complex networks [30]. With recent technological advances, huge sets of data are accumulating at a tremendous pace in vari- ous ﬁelds of human activity (including telecommunication, the internet, stock markets) and in many areas of life and social sciences (biomolecular assays, genetic maps, groups of web users, etc.). Understanding both the universal and speciﬁc features of the networks associated with these data has become an actual and important task. The knowledge of the community structure enables the prediction of some essential features of the systems under investigation. For example, since with our approach it is possible to “zoom” onto a single unit in a network and uncover its communities (and the communities connected to these, and so on), we provide a tool to interpret the local organisation of large networks and can predict how the modular structure of the network changes if a unit is removed (e.g., in a gene knock out experiment). A unique feature of our method is that we can simultaneously look at the network at a higher level of organisation and locate the communities that play a key role within the web of communities. Among the many possible applications is a more sophisticated approach to the spreading of infections (e.g., real or computer viruses) or information in highly modular complex systems. References [1] Watts, D. J. & Strogatz, S. H. Collective dynamics of ’small-world’ networks. Nature 393, 440–442 (1998). [2] Barab´asi, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999). [3] Albert, R. & Barab´asi, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002). [4] Mendes, J. F. F. & Dorogovtsev, S. N. Evolution of Networks: From Biological Nets to the Internet and WWW (Oxford University Press, Oxford, 2003). [5] Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z., & Barab´asi, A.-L. Hierarchical organization of modularity in metabolic networks. Science 297, 1551–1555 (2002). [6] Spirin, V. & Mirny, L. A. Protein complexes and functional modules in molecular networks. Proc. Natl. Acad. Sci. USA 100, 12123–12128 (2003). [7] Onnela, J.-P., Chakraborti, A., Kaski, K., Kert´esz, J., & Kanto, A. Dynamics of market correlations: Taxonomy and portfolio analysis. Phys. Rev. E 68, 056110 (2003). 8

分享到：

赞收藏

资料库

CPM算法（Uncovering_the_overlapping_community....pdf

相关推荐

行业

热门标签

最新资料