遗传算法用于NP 完全问题的求解.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.31M 资料格式：pdf 举报版权申诉

sd_junxi-1828329-4744302543287604317.pdf-第1页.png

第1页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第2页.png

第2页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第3页.png

第3页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第4页.png

第4页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第5页.png

第5页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第6页.png

第6页 / 共7页

sd_junxi-1828329-4744302543287604317.pdf-第7页.png

第7页 / 共7页

文本预览

2 2 2 2 2 2 2 第 36 卷　第 2 期 Vol. 36 　No. 2 　　　　　　文章编号 :0559 7234 (2001) 02 0171 07 山　东　大　学　学　报 (自然科学版) JOURNAL OF SHANDON G UN IV ERSIT Y 　　　　2001 年 6 月 J un. 2001 遗传算法用于 NP 完全问题的求解杨　青1 　马　军2 (1. 山东公安专科学校 ,山东济南 250014 ; 2. 山东大学计算机系 ,山东济南 250100) 摘要 :讨论了如何利用遗传算法求解布尔表达式的可满足性问题 ,并给出该结果对求解其他 N P 完全问题时的应用. 关键词 :遗传算法 ;布尔表达式可满足问题 ;N P 中图分类号 : TP301 　　　文献标识码 :A 完全问题遗传算法是基于生物学进化原理的一种全局搜索算法 ,通过用计算机模拟生物进化过程 ,使群体不断优化 ,并在变化过程中找出最优解. 其特点是简单、通用、鲁棒性强和适于并行处理. 把遗传算法用于求解 N P 完全问题 ,可为求解 N P 完全问题给出新的思路. 遗传算法的框架是由 Holland[ 1 ]于本世纪 60 年代提出的 ,可描述为 : 1) 随机产生初始种群 ; 2) 利用适应度函数对个体计算函数值 ; 3) 按一定的概率选择对个体进行选择、交叉、变异等操作产生新种群 ; 4) 重复 2 、3 两步 ,直到收敛. (找到最佳解或迭代次数充分多 ,停止计算. ) N P 完全问题通常被认为是一些人们难以在有限的时间、空间内对问题求出最佳解的问题[ 2 ] . 目前人们对 N P 完全问题通常采用以下二种方法进行求解 : ①舍去寻找最优解的要求 ,寻找对一般问题比较接近最优解的近似解 ; ②利用非常规的求解技术求解 ,其中包括利用神经网络和遗传算法进行问题求解[ 1 ,3～9 ] . 布尔表达式的可满足性问题 (以下简称 SA T 问题) 是 N P 完全问题中的核心问题. 已证明 ,对任意 N P 完全问题求解 ,均可以转化为对 SA T 问题的求解 ,并且转化算法为多项式时间的. 尽管在理论上 ,所有 N P 完全问题的求解难度是相同的 ,但并非所有的 N P 完全问题都可以很容易地表示为适合于应用遗传算法的表达式 ,如旅行商问题[ 5 ] . 所以若能很好地对 SA T 问题进行求解 ,对其他不适宜表示成遗传算法表达式的问题 ,可在多项式时间内将其转化为一个对 SA T问题求解问题 ,然后求解 SA T问题 ,并把其结果在收稿日期 :2000 05 基金项目 :国家 863 作者简介 :杨青 (1972 - ) ,女 ,讲师 ,在读硕士生. 研究方向为遗传算法、近似算法. 22 306 主题 (863 ZT06 306 01 4) 和山东省自然科学基金 ( Z99 G01) 资助项目.

271 　　　　　　　　山　东　大　学　学　报 (自然科学版) 　　　　　　　　　第 36 卷多项式时间内变换成为到原问题的解. 本文主要讨论了利用遗传算法求解 SA T 问题的方法 ,并同时讨论了对其他 N P 完全问题的应用. 因目前还难于对遗传算法的性能给出精确的数学分析 ,故本文采用国际上目前评价遗传算法性能的惯用方法 ,对几个典型实例给出了计算机模拟实验结果. 1 　SA T 问题 SA T 可描述为对任意给出的布尔变量表达式 F ( x 1 , x 2 , …, x n) , 判断是否存在一个对其变量 x 1 , x 2 , …, x n 的真值指派使表达式 F 的值为真. 显然对 SA T 问题的真值指派可用向量 ( x 1 , x 2 , …, x n) 表示. 其中让 x i ∈{ 0 ,1} ,0 表示 x i 取假 ;1 表示 x i 取真. 这种表达式非常适合用遗传算法求解 ,如长度固定 ,可用二进制表示 , 且一个位的变化不会影响其它位的值等. 适应度函数是遗传算法设计中的关键要素之一. 对 SA T 问题的适应度函数最简单的方法是定义 val ( Ci) = 1 if ( x 1 , x 2 , …, x n) 使 Ci 为“真”,否则为 0 , Ci 为一子句. 进一步定义对逻辑运算 not ,or 和 and 的函数值 :设 Ci 为任意字句 ,定义 val (not Ci) = 1 - val ( Ci) ; val (or C1 , …, Cn) = max (val ( C1) , …,val ( Cn) ) ; val (and C1 , …, Cn) = ave (val ( C1) , …,val ( Cn) ) = 例如 ,对布尔表达式 x 1 and ( x 1 or 珔x 2) ,由下表给出函数 Val 的值. 从这个例子来看 , 1 val ( Ci) . 1 n ∑n 表 1 　适应度函数的值 Table 1 　The value of payoff function x 1 x 2 适应度函数的值 0 0 1 1 0 1 0 1 (ave0 (max (0 , (1 0) ) ) ) = 0. 5 (ave0 (max (0 , (1 - 1) ) ) ) = 0. 0 (ave1 (max (1 , (1 - 0) ) ) ) = 1. 0 (ave1 (max (1 , (1 - 1) ) ) ) = 1. 0 只有当适应度函数值为 1 时 (第 3 ,4 行) ,所对应的解是正确的 , 否则不正确. 但引入上述定义后 ,比较两个布尔表达式相等与否 ,不能仅从其对应的适应度函数值来判断 , 否则可能会引起矛盾. 如表 2 和表 3 所给出的布尔表达式 ( ( x 1 and x 2) and x 3) 、( x 1 and ( x 2 and x 3) ) 的适应度函数值 , ave ( ave ( x 1 , x 2 ) x 3 ) ≠ave ( x 1 ave ( x 2 , x 3 ) ) , 根据上文定义 , 表 2 　适应度函数的值表 3 　适应度函数的值 Table 2 　The value of payoff function Table 3 　The value of payoff function x 1 x 2 x 3 适应度函数的值 x 1 x 2 x 3 适应度函数的值 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 (ave (ave0 ,0) 0) = 0 (ave (ave0 ,0) 1) = 0. 5 (ave (ave0 ,1) 0) = 0. 25 (ave (ave0 ,1) 1) = 0. 75 (ave (ave1 ,0) 0) = 0. 25 (ave (ave1 ,0) 1) = 0. 75 (ave (ave1 ,1) 0) = 0. 5 (ave (ave1 ,1) 1) = 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 (ave0 (ave0 ,0) ) = 0 (ave0 (ave0 ,1) ) = 0. 25 (ave0 (ave1 ,0) ) = 0. 25 (ave0 (ave1 ,1) ) = 0. 5 (ave1 (ave0 ,0) ) = 0. 5 (ave1 (ave0 ,1) ) = 0. 75 (ave1 (ave1 ,0) ) = 0. 75 (ave1 (ave1 ,1) ) = 1

第 2 期　　　　　　　　　杨青等 :遗传算法用于 NP 完全问题的求解　　　　　　　　　　 371 可推出 val ( ( x 1 and x 2) and x 3) ≠val ( x 1 and ( x 2 and x 3) ) ,显然 ,这违背了对 and 的结合律. 但是我们可以规定只有当适应度函数值为 1 时 ,解是正确的 ;否则 ,解不正确. 在上两表中 ,前 7 个解都不正确 ,仅第 8 个解正确. 从这个意义上讲 ,val ( ( x 1 and x 2) and x 3) = val ( x 1 and ( x 2 and x 3) ) , 不违背 and 的结合律. 即使如此 , 仍然存在其他问题. 对式 x 1 and x 2 , 由表 4 给出函数的 val 值 ,显然 ,第 1 ～ 3 行都是正确解 ,但 2 、3 行适应度函数值不为 1 ,这与上文发生矛盾. 经分析发现 ,只有 F 中包含 ( …and …) 子句时 ,才会出现这个问题. 可用 De Morgn 定律将否定运算深入到每个变量 ,如将 x 1 and x 2 转换为 x 1or x 2 ,则问题可被解决. 所以在采用上述适应度函数时 , 可以要求首先把 F 化为析取范式或合取范式 ,而这个转化可以在线性时间内完成[10 ] . 表 4 　适应度函数的值 Table 4 　The value of payoff function x 1 x 2 适应度函数的值 0 0 1 1 0 1 0 1 1 1 1 1 ave (0 ,0) = 1 ave (0 ,1) = 0. 5 ave (1 ,0) = 0. 5 ave (1 ,1) = 0 2 　用遗传算法解 SA T 问题以下给出算法的主要步骤. 步骤 1 　建立一个初始种群 P = { X 1 , X 2 , …, X n} ,其中 , X i = { x 1 x 2 , …, x m } (1 ≤ i ≤ n) 是一串二进制表达式. g = 0 , g 代表进化过程中的繁衍代数 , n 代表样本总数 , m 代表二进制表达式的长度 ; 步骤 2 　对当前种群 P 中每一个体计算 f ( X i) . if ( f ( X i) = 1) 　{ 停止计算 ,返回问题解 X i 以及迭代次数 g} else 　{ 标记当前种群最优解 X b 及当前种群最大适应度函数值 f b = f ( X b) } . 标记开始计算以来最优解 X max 及对应最大的适应度函数值 f max = f ( X max) . If ( f b > f max) 　f max = f b ; 　s = 0 ; else 　s = s + 1 ; 若 s 足够大 , 停止计算 ; (迭代次数足够大 , 最大适应度函数值 f max 不增长 , 停止计算. )

471 　　　　　　　　山　东　大　学　学　报 (自然科学版) 　　　　　　　　　第 36 卷步骤 3 　初始化交配池 M 和后代 O M = O = ; ; 步骤 4 　for i = 1 to n do 　{ 从当前种群 P 中用随机的方法选择一个个体 X i ; M = M ∪ X i} ; 步骤 5 　交叉在 M 中按交叉概率 PC 选择交叉父代 ,对交叉父代随机配对 ,并在随机产生的交叉位置进行交叉 ,生成交叉子代 ; 　　　　O = ( M - { 交叉父代} ) ∪{ 交叉子代} ; 步骤 6 　变异设 O = { Y 1 , Y 2 , …, Y n} ,对 Y i 中的每一位按变异概率 Pm 进行变异 ; 步骤 7 　替换假设 X b 是上一代种群 P 中的最优解 , Y b 是新产生子代 O 中最差解 : P = ( O - { Y b} ) ∪{ X b} ; g = g + 1 ; 步骤 8 　goto 步骤 2. 3 　实验结果现在分别以 3 种表达式为例 ,说明利用遗传算法求解 SA T 的情况. 表达式 1 : ( x 1 ∧ x 2 ∧ … ∧ x m ) ∨ ( x 1 ∧ x 2 ∧ … ∧ x m ) ; 表达式 2 : ( x 1 ∧ x 2 ∧ … ∧ x m ) ∨ ( x 1 ∧ x 1 ∧ x 2 ∧ … ∧ x m ) ; 表达式 3 :任意具有 n 个以上真值指派的布尔表达式. 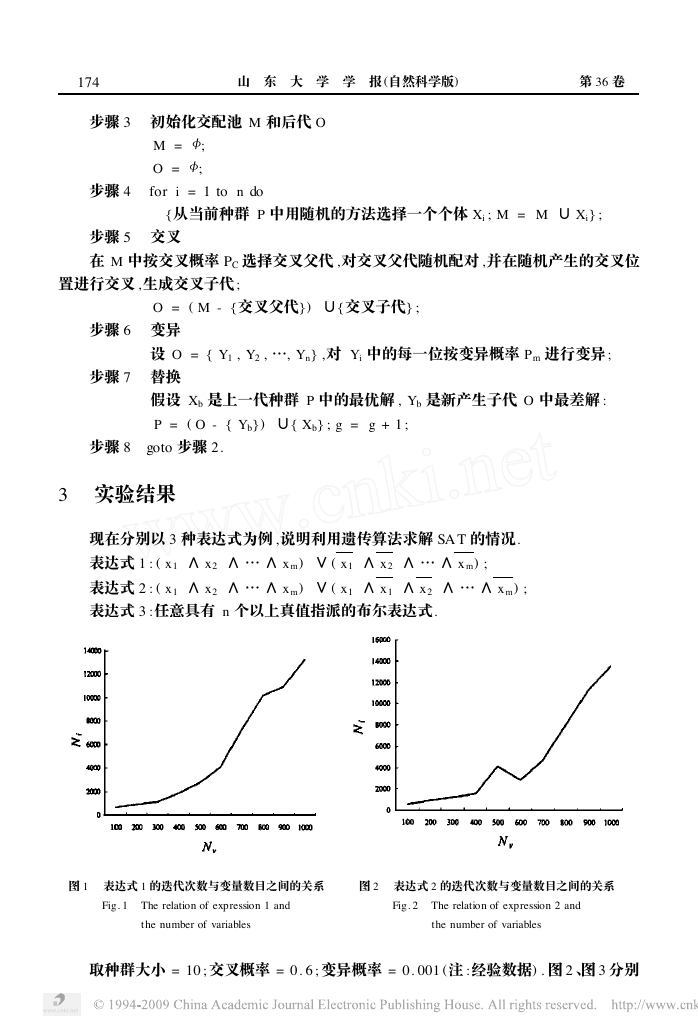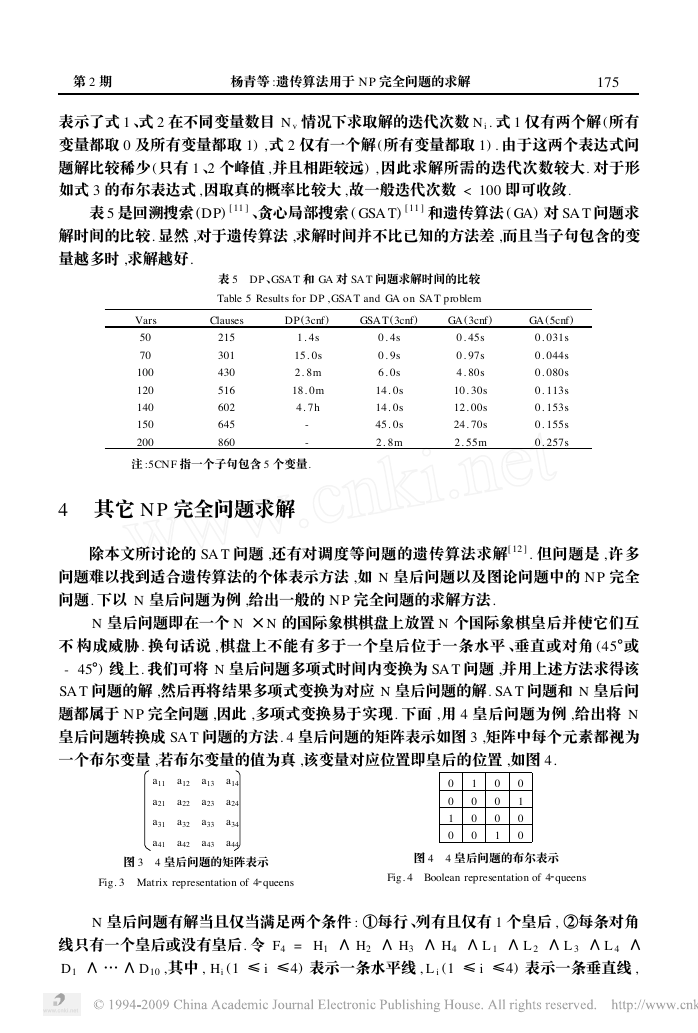图 1 　表达式 1 的迭代次数与变量数目之间的关系图 2 　表达式 2 的迭代次数与变量数目之间的关系 Fig. 1 　The relation of expression 1 and Fig. 2 　The relation of expression 2 and the number of variables the number of variables 取种群大小 = 10 ;交叉概率 = 0. 6 ;变异概率 = 0. 001 (注 :经验数据) . 图 2 、图 3 分别

2 2 第 2 期　　　　　　　　　杨青等 :遗传算法用于 NP 完全问题的求解　　　　　　　　　　 571 表示了式 1 、式 2 在不同变量数目 N v 情况下求取解的迭代次数 N i . 式 1 仅有两个解 (所有变量都取 0 及所有变量都取 1) ,式 2 仅有一个解 (所有变量都取 1) . 由于这两个表达式问题解比较稀少 (只有 1 、2 个峰值 ,并且相距较远) , 因此求解所需的迭代次数较大. 对于形如式 3 的布尔表达式 ,因取真的概率比较大 ,故一般迭代次数 < 100 即可收敛. 表 5 是回溯搜索 (DP) [ 11 ] 、贪心局部搜索 ( GSA T) [ 11 ] 和遗传算法 ( GA) 对 SA T 问题求解时间的比较. 显然 ,对于遗传算法 ,求解时间并不比已知的方法差 ,而且当子句包含的变量越多时 ,求解越好. 表 5 　DP、GSAT 和 GA 对 SAT 问题求解时间的比较 Table 5 Results for DP , GSAT and GA on SAT problem Clauses DP(3cnf) GSAT(3cnf) GA (3cnf) 215 301 430 516 602 645 860 1. 4s 15. 0s 2. 8m 18. 0m 4. 7h - - 0. 4s 0. 9s 6. 0s 14. 0s 14. 0s 45. 0s 2. 8m 0. 45s 0. 97s 4. 80s 10. 30s 12. 00s 24. 70s 2. 55m GA (5cnf) 0. 031s 0. 044s 0. 080s 0. 113s 0. 153s 0. 155s 0. 257s Vars 50 70 100 120 140 150 200 　　　　　　注 :5CNF 指一个子句包含 5 个变量. 4 　其它 N P 完全问题求解除本文所讨论的 SA T 问题 ,还有对调度等问题的遗传算法求解[ 12 ] . 但问题是 ,许多问题难以找到适合遗传算法的个体表示方法 ,如 N 皇后问题以及图论问题中的 N P 完全问题. 下以 N 皇后问题为例 ,给出一般的 N P 完全问题的求解方法. N 皇后问题即在一个 N ×N 的国际象棋棋盘上放置 N 个国际象棋皇后并使它们互不构成威胁. 换句话说 , 棋盘上不能有多于一个皇后位于一条水平、垂直或对角 (45°或 - 45°) 线上. 我们可将 N 皇后问题多项式时间内变换为 SA T 问题 ,并用上述方法求得该 SA T 问题的解 ,然后再将结果多项式变换为对应 N 皇后问题的解. SA T 问题和 N 皇后问题都属于 N P 完全问题 ,因此 ,多项式变换易于实现. 下面 ,用 4 皇后问题为例 ,给出将 N 皇后问题转换成 SA T 问题的方法. 4 皇后问题的矩阵表示如图 3 ,矩阵中每个元素都视为一个布尔变量 ,若布尔变量的值为真 ,该变量对应位置即皇后的位置 ,如图 4. a11 a21 a31 a41 a12 a22 a32 a42 a13 a23 a33 a43 a14 a24 a34 a44 0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 图 3 　4 皇后问题的矩阵表示 Fig. 3 　Matrix representation of 4 queens 图 4 　4 皇后问题的布尔表示 Fig. 4 　Boolean representation of 4 queens N 皇后问题有解当且仅当满足两个条件 : ①每行、列有且仅有 1 个皇后 , ②每条对角线只有一个皇后或没有皇后. 令 F4 = H1 ∧ H2 ∧ H3 ∧ H4 ∧ L 1 ∧ L 2 ∧ L 3 ∧ L 4 ∧ D1 ∧ … ∧ D10 ,其中 , Hi (1 ≤ i ≤4) 表示一条水平线 , L i (1 ≤ i ≤4) 表示一条垂直线 ,

671 　　　　　　　　山　东　大　学　学　报 (自然科学版) 　　　　　　　　　第 36 卷 D i (1 ≤i ≤10) 表示一条对角线. 根据定义 ,以第一行为例对 F4 行、列做转换. 因为 ,每行只能包含一个皇后 , H1 对应布尔表达式为 : 　　　　　　(or (and a11 a12 a13 a14) (and a11 a12 a13 a14) (and a11 a12 a13 a14) (and a11 a12 a13 a14) ) 根据转换 ,若第一行有且只有一个皇后 , 只需令对应皇后位置的布尔变量值为 1 , 其它位置的布尔变量值为 0 , H1 对应的布尔表达式即可满足 ;反之 , 若 H1 对应的布尔表达式可满足 ,则第一行有且只有一个皇后 ,其位置即值为 1 的布尔变量所在的位置. 其它行、列的转换过程与 H1 的转换过程相似. 对角线的转换以 a21 a12 (设 a21 a12 为 D1) 为例 , D1 可表示为 : 　　　　　　(or (and a21 a12) (and a21 a12) (and a21 a12) ) 若对角线只有 1 个皇后 ,令皇后位置的变量为 1 ,其他为 0 ,表达式前两行中必定有一行值为 1 ;若没有皇后 ,令该对角线上所有变量值为 0 ,则最后一行值为 1. 因此 ,若对角线上只有一个皇后或没有皇后 , D1 一定为 1. D1 为 1 时 ,若前两行中有一行值为 1 ,该对角线有一个皇后 ,其位置在值为 1 的变量位置 ;若最后一行值为 1 , 该对角线上所有变量值为 0 , 即该对角线没有皇后. 因此 , D1 为 1 时 ,该对角线只有 1 个皇后或没有皇后. 其他对角线转换同理. 由转换过程可知 ,若 4 皇后问题有解 ,则满足 ①②两个条件 ,所有的 Hi 、D i 、L i 值为 1 , F4 为真 ;反之 ,若 F4 为真 ,所有 Hi 、D i 、L i 的值必定为 1 , ①②两个条件被满足 ,4 皇后问题有解. 同理 ,若 N 皇后问题有解 ,只需令对应皇后位置的变量为 1 ,其它变量为 0 ,则相应的 SA T 问题有解 ;反之 ,若 SA T 问题有解 ,仅在值为 1 的变量所在位置安置皇后即可 , 其转换也是多项式时间的. 5 　结束语因 SA T 问题的表示、适应度函数的选取 ,比较适合于遗传算法 ,又因大多 SA T 问题的实例有许多可满足的真值指派 ,即其搜索空间中有许多等高的峰 ,非常适合于遗传计算. 通常对这样的 SA T 问题的实例 ,只需很少的迭代次数便可找到真值指派. 本文的计算机模拟又表明 ,若 SA T 的实例确实有解 ,即使对只有一、两解的实例 (具有单峰或相距较远的双峰) ,若变量数目 n 在 1000 之内 ,也可以在较少的迭代次数内判定. 因 SA T 问题为 N P 完全问题的核心问题 ,求解其它 N P 完全问题 ,可先将其转换为 SA T 问题 ,然后将对应 SA T 问题的解转换为原问题的解. 这样可以避开对某些问题难以找出适合遗传计算的表达式的困难. 故本文给出一种利用遗传算法求解 N P 完全问题的一般框架.

第 2 期　　　　　　　　　杨青等 :遗传算法用于 NP 完全问题的求解　　　　　　　　　　 771 参考文献 : [ 1 ] Holland J . Adaptation in Natural and Artificial Systems[ M ] . Ann Arbor : The University of Michigan Press ,1975. [ 2 ] Hochbaum D. Approximation Algorithms for NP hard Problems[ M ] . Berkeley ,CA : PWS Publishing Company ,1997. [ 3 ] Hou E S H ,Ansari N ,Ren H. A genetic algorithms for multiprocessor scheduling[J ] . IEEE Trans. Parallel and Distribut ed Systems ,1994 ,5 (2) :113～120. [ 4 ] De Jong K A. Genetic Algorithms :A 10 Year Perspective[ A ] . in : Proceedings of the First International Conference on Genetic Algorithms , Grefenstette J J ,Hillsdale ,NJ :Lawrence Erlbaum Associates Publishers ,1985 ,169～177. [ 5 ] Gold berg D ,Lingle R. Alleles ,Loci and the Traveling Salesman Problem[ A ] . In :Same to [ 4 ] . 154～159. [ 6 ] Grefenstette J J , Gopal R ,Rosmaita B , Gucht D. Genetic Algorithms for the Travelling Salesman Problem[ A ] . In : Same to [ 4 ] ,160～168. [ 7 ] Smith D. Bin Packing with Adaptive Search[ A ] . In :Same to [ 4 ] ,202～207. [ 8 ] Davis L . Handbook of Genetic Algorithms[ M ] . New York :Van Nostrand Reinhold Publishers ,1991. [ 9 ] Goldberg D E. Genetic Algorithms in Search ,Optimization and Machine Learning[ M ] . New York :Addison Wesley Pub lishing Company ,1989. [ 10 ] Nilsson N J . Artificial Intelligence ,A New Synthesis[ M ] . New York :Morgan Kanfmann Publishers ,1998. [ 11 ] Selman B ,Levelsque H J ,Mitchell D. A New Method for Solving Hard Satisfiabilit y Problems[ A ] . In : Proceedings of the Tenth National Conference on Artificial Intelligence (AAAI - 92) , Whitley L ,San Jose ,CA :Duxpury press ,J uly , 1992 ,440～446. [ 12 ] 玄光男 ,程润伟. 遗传算法与工程计算[ M ] . 汪定伟等译. 北京 :科学出版社 ,2000. SOL V IN G N P COMPL ETE PROBL EMS B Y GEN ETIC AL GORITHMS YAN G Qing1 ,MA J un2 (1. Dept . of B asic Cou rses , S handong Public Secu rity College , Ji nan 250014 , S handong , Chi na ;2. Dept . of Com puter Science , S handong U niv . , Ji nan 250100 , S handong , Chi na) Abstract :How to solve t he Boolean Satisfiability Problem (SA T) by genetic algorit hms is dis cussed. The applications of t he results for ot her N P Key words :genetic algorit hm ;Boolean satisfiability problem ;N P Complete problems are also shown. complete problems

分享到：

赞收藏

资料库

遗传算法用于NP 完全问题的求解.pdf

相关推荐

开发技术

热门标签

最新资料