2019年福建小升初数学真题及答案.doc

发布时间：2022-09-03 发布人：admin 分类：说明书资料大小：0.14M 资料格式：doc 举报版权申诉

第1页 / 共6页

第2页 / 共6页

第3页 / 共6页

第4页 / 共6页

第5页 / 共6页

第6页 / 共6页

文本预览

2019 年福建小升初数学真题及答案 (试卷满分 100 分，考试时间 90 分钟) 题号填空题选择题计算题应用题总分得分一、填空题。（1-2 小题每空 1 分，3-8 小题，每小题 2 分，共 18 分） 1. 七五折＝( ) %＝＝( （） 16 )(填小数) 2. 2550毫升=（）升 4米7厘米＝( )厘米 3.6小时=( )分 3．王老师到商店去买5个篮球和3个足球，需要348元，如果买3个篮球和2个足球，需要216 元，一个篮球( ) 元。 4. 用一个小数减去末位数字不为零的整数,如果给整数添上一个小数点,使它变成小数,差就增加 154.44, 这个整数是（）。 5. 客车速度每小时 72 千米,货车速度每小时 60 千米,两列火车相向而行,货车每节车厢长 10 米,火车头与车尾守室长相当于两节车厢,每节车厢装 50 吨含铁 60%的铁矿石,客车司机发现这列货车从他身边过时共花时间 12 秒,问这货车装的铁矿石共可炼铁（）吨。 6. —个圆柱体，如果把它的高截短 6 厘米，表面积就减少 75.36 平方厘米，则体积减少（）立方厘米。 7. 已知小强比小刚早出生6年，今年小强的年龄是小刚年龄的2倍少3岁，那么两人今年的年龄之和是（）岁。 8. 有一个最简分数，把分子加上分母，分母也加上分母，所得到的新分数是原分数的9倍，这个最简分数是（）。二、选择：（每题 2 分，共 10 分） 1. 与 4%不相等的数是（） A. 0.04 B. 4 C. 4/100 2. 用丝带捆扎一种礼品盒如下，结头处长 25 厘米，要捆扎这种礼品盒需准备( )分米的丝带比较合理。

A. 21.5 分米 B. 23 分米 C. 30 分米 3. 一个平行四边形的一组邻边分别长 8 厘米和 12 厘米，平行四边形的一条高是 10 厘米，这个平行四边形的面积是（）。 A. 80 平方厘米 B. 120 平方厘米 C. 80 平方厘米或 120 平方厘米 4. 甲、乙两堆煤，从甲堆中运 A. 1 5 B. 2 5 1 5 给乙，则两堆煤相等，原来甲比乙多（）。 C. 2 3 5.一瓶油4/5千克，先倒出它的1/5，再往瓶里加1/5千克。现在瓶内的油比原来( )。 A. 增多 B. 减少 C. 不变三、算一算。（共 36 分） 1. 直接写出得数。（8 分） × 6 = 5 6 2 5 9.2 + 4.7= 3 4 1 3 + = 1.5×0.06= 1 6 46 - 3 5 = 8÷2.5= 8.3-5.6= 8 1 9 ÷ 1 2 3 = 1 5 ÷ 2. 能简算的要简算。（9 分） 14×96÷7 18×（200＋ 1 18 ） 5 8 ×50%÷0.125× 3. 求未知数的值。（9 分） x- 1 3 =1.4 6×3﹣1.8x＝7.2 2 5 ：3.5＝ 6 7 ：x

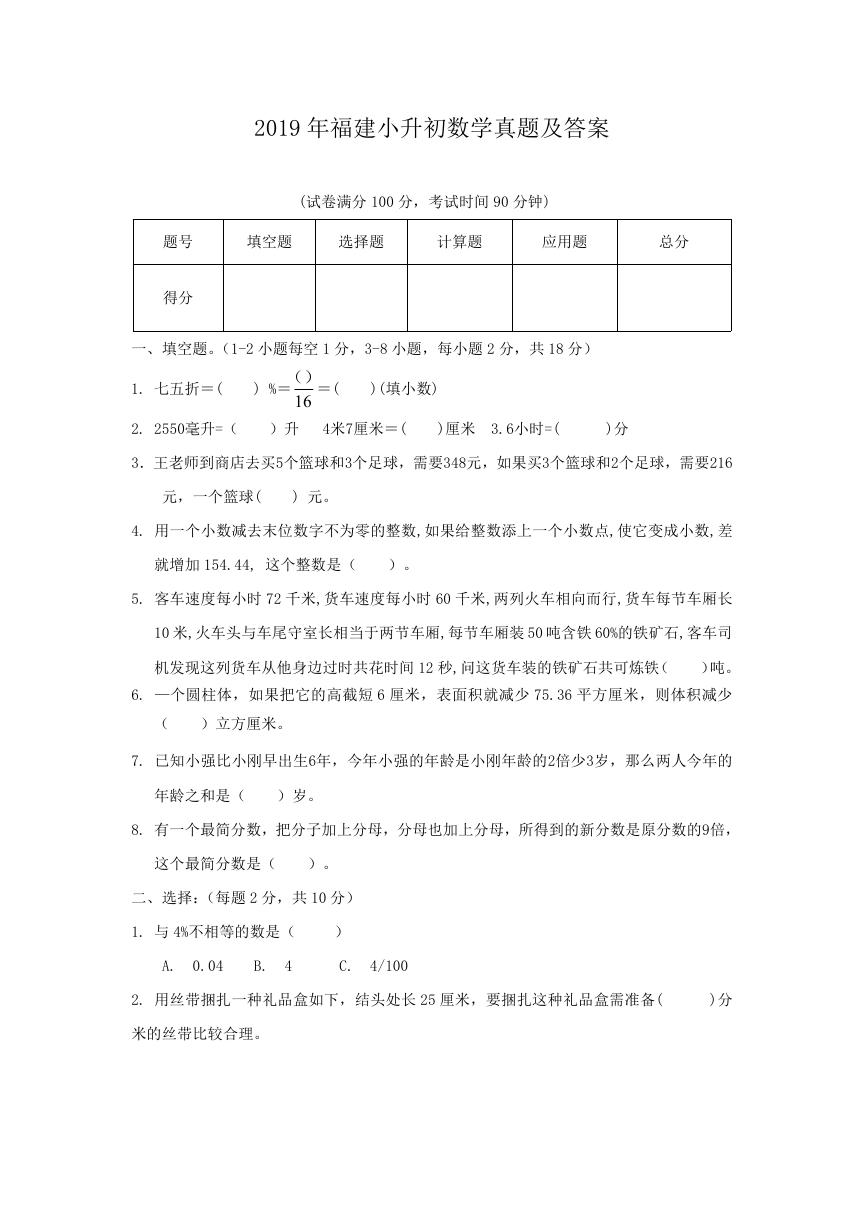
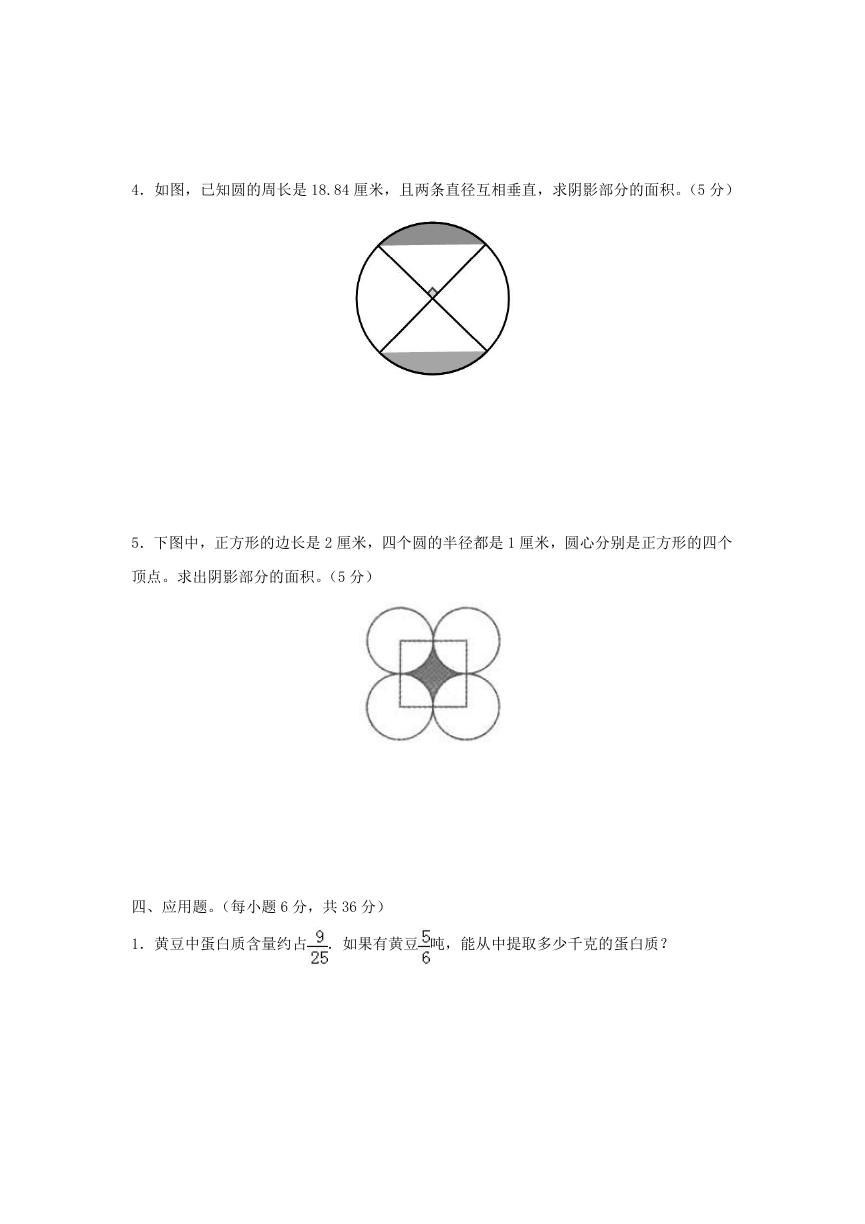
4．如图，已知圆的周长是 18.84 厘米，且两条直径互相垂直，求阴影部分的面积。（5 分） 5．下图中，正方形的边长是 2 厘米，四个圆的半径都是 1 厘米，圆心分别是正方形的四个顶点。求出阴影部分的面积。（5 分）四、应用题。（每小题 6 分，共 36 分） 1．黄豆中蛋白质含量约占．如果有黄豆吨，能从中提取多少千克的蛋白质？

2．北京四环路上分布着不同规模的桥梁 147 座．其中立交桥数量占桥梁总数的，人行天桥占桥梁总数的，这两种桥共有多少座？ 3. 某石油进口国九月的石油进口量比八月减少了 5%，由于国际油价上涨，九月进口石油的费用比八月增加了 14%，求九月石油价格比八月增长了百分之多少？ 4. 一项工作，两个师傅和三个徒弟合作需要 22 天完成，如果三个师傅和两个徒弟合作需 9 要 12 天完成，如果一名徒弟单独做需多少天完成？ 7 5. 甲、乙、丙三人都在银行有存款，乙的存款数比甲的2倍少100元，丙的存款数比甲、乙两人的存款和少300元，甲的存款是丙的 2 5 ，那么甲、乙、丙共有存款多少元? 6. 商店里有大、中、小规格的弹子盒子,分别装有同样规格的弹子 13、11、7 粒.如果有人要买 20 粒,那么不必拆盒(一大盒加一小盒即可)如果要买 23 粒,就必须拆盒卖,你能不能找出一个最小数,凡是来买弹子的数目超过这个数,肯定不必拆开盒子卖,请说明理由?

一、填空题。（1-2 小题每空 1 分，3-8 小题，每小题 2 分，共 18 分）参考答案 1. 75 12 0.75 2. 2.55 407 216 3. 48 4. 156 5. 1260. 6. 75.36 7. 24 8. 二、选择：（每题 2 分，共 10 分） 1.B 2.B 3.A 4. C 5. B 三、算一算。（共 36 分） 1. 13.9 0.9 3.2 2.7 2. 192 3601 1 3. 2.1 6 7.5 11 12 193 30 1 17 2 3 1 0 8 4. 圆的半径为 18.84÷ 3 . 1 4 ÷ 2 = 3 厘米 [3×3×3.14﹣（3+3）×3] ÷ 2 = 5 . 1 3 平方厘米 5．2×2-1×1×3.14=0.86（平方厘米）四、应用题。（每小题 6 分，共 36 分） 1． × = （吨）；吨=300（千克）；答：能从中提取 300 千克的蛋白质 2．147×（）=147× =93（座）,答：两种桥共有 93 座。 3. [100×l00×(l＋14%)÷95－100] ÷100=20% 答：九月石油价格比八月增长了 20%。 4. (1÷ 22 ＋1÷ 9 12 )÷5＝ 7 11 60 1÷ 22 － 9 11 ×2＝ 60 1 12 1÷ 1 ＝12（天） 12 答：一名徒弟单独做需要 12 天。 5. 解：设甲为x元，乙即为（2x-100）元，丙即为（3x-400）元。列方程： 2 5 （3x-400）=x 解得：x=800（元）则乙 2×800-100= 1500（元）、丙 3×800-400=2000（元） 800+1500+2000=4300（元）答：甲、乙、丙共有存款 4300 元. 6 .这个数是 30.

因为 31=7+11+13, 32=7×3+11, 33=7+13×2, 34=7×3+13, 35=11×2+13, 36=11×2+7×2, 37=11+13×2. 这七个连续整数均不须拆开盒子卖,故以后可在每个数的基础上,加上 7 的若干倍就可以了.

分享到：

赞收藏

资料库

2019年福建小升初数学真题及答案.doc

相关推荐

小升初

热门标签

最新资料