基于OS-ELM的风速修正及短期风电功率预测.pdf-资料库

weixin_38684328-12941700-rticle-3000017011.pdf-第1页.png

第1页 / 共6页

weixin_38684328-12941700-rticle-3000017011.pdf-第2页.png

第2页 / 共6页

weixin_38684328-12941700-rticle-3000017011.pdf-第3页.png

第3页 / 共6页

weixin_38684328-12941700-rticle-3000017011.pdf-第4页.png

第4页 / 共6页

weixin_38684328-12941700-rticle-3000017011.pdf-第5页.png

第5页 / 共6页

weixin_38684328-12941700-rticle-3000017011.pdf-第6页.png

第6页 / 共6页

基于基于OS-ELM的风速修正及短期风电功率预测的风速修正及短期风电功率预测随着时间的推移，风电场风电功率预测模型的适用性逐渐降低，导致预测精度下降。为了解决该问题，基于在线序列-极限学习机(OS-ELM)算法提出了风电场短期风电功率预测模型的在线更新策略，建立的OS-ELM模型将风电场的历史数据固化到隐含层输出矩阵中，模型更新时，只需将新产生的数据对当前网络进行更新，大大降低了计算所需的资源。采用极限学习机(ELM)算法对数值天气预报(NWP)的预测风速进行修正，并根据风电功率的置信区间对预测功率进行二次修正。实验结果表明，采用OS-ELM算法更新后的模型适用性增强，预测精度提高；采用基于风电功率置信区间的功率修正模型后，风电功率的预测精度明显提高。 0 引言引言随着全球化石能源储量的日渐匮乏以及环境问题的日益突出，新能源的开发与利用受到人们的广泛关注。在众多新能源中，风能作为环保清洁的可再生能源具有储量大、分布广等优势，日益受到各个国家的重视[1]。然而，与常规能源不同，风电具有间歇性和波动性特点，给电力系统的安全、稳定运行以及保证电能质量带来了巨大的压力[2]。对风电功率进行准确的预测，将有助于削弱风电接入对电网造成的不利影响，保证了电力系统的安全、稳定[3-4]。在短期风电功率预测方面，国内外学者做了大量的研究，常用的统计学习方法包括卡尔曼滤波法、模糊预测法以及支持向量机等。总结目前国内外的研究现状可知，前人的研究主要集中在如下4点：(1)数据预处理。为了提高风能到电能转换的模型精度，提出了很多数据预处理的方法，如小波分析法[5]、经验模态分解法[6-7]、混沌时间序列法[8]以及数据挖掘中的聚类分析[9]等。(2)利用寻优算法对模型参数进行优化，如粒子群算法、遗传算法[10-11]等。(3)研究风速风向对功率影响较多，很少考虑其他气象要素对风电机组出力的影响。(4)研究风速到风电功率的转化模型较多，而研究风速及风电功率的统计修正较少。风电功率预测模型随着风电场季节及训练样本的变化不断调整，需要模型能根据新样本实时更新。但是传统神经网络模型由于训练样本不变，随着训练时间的延长，该模型会导致预测结果越来越不准确，因此为了提高整个训练网络的外延能力，需要不断地更新样本数据。但是样本数量的增加也造成了训练所需要的资源显著增加。针对上述问题，本文提出了在线序列极限学习机(OS-ELM)算法，解决了模型更新问题，同时基于极限学习机算法建立了 1 OS-ELM算法原理算法原理式(2)中，H被称为隐含层输出矩阵，β表示输出权值矩阵，T表示网络的输出矩阵。求解以下方程组的最小二乘解可得β 为了更好地适应短期风电功率预测模型的在线更新，引入OS-ELM。OS-ELM算法主要包括两个步骤[12-13]： (1)初始化阶段：给定网络初始的隐含层节点数，输入初始训练样本数据，初始化网络并设置网络参数，求得初始隐含层输出矩阵H0和输出权值向量β0。

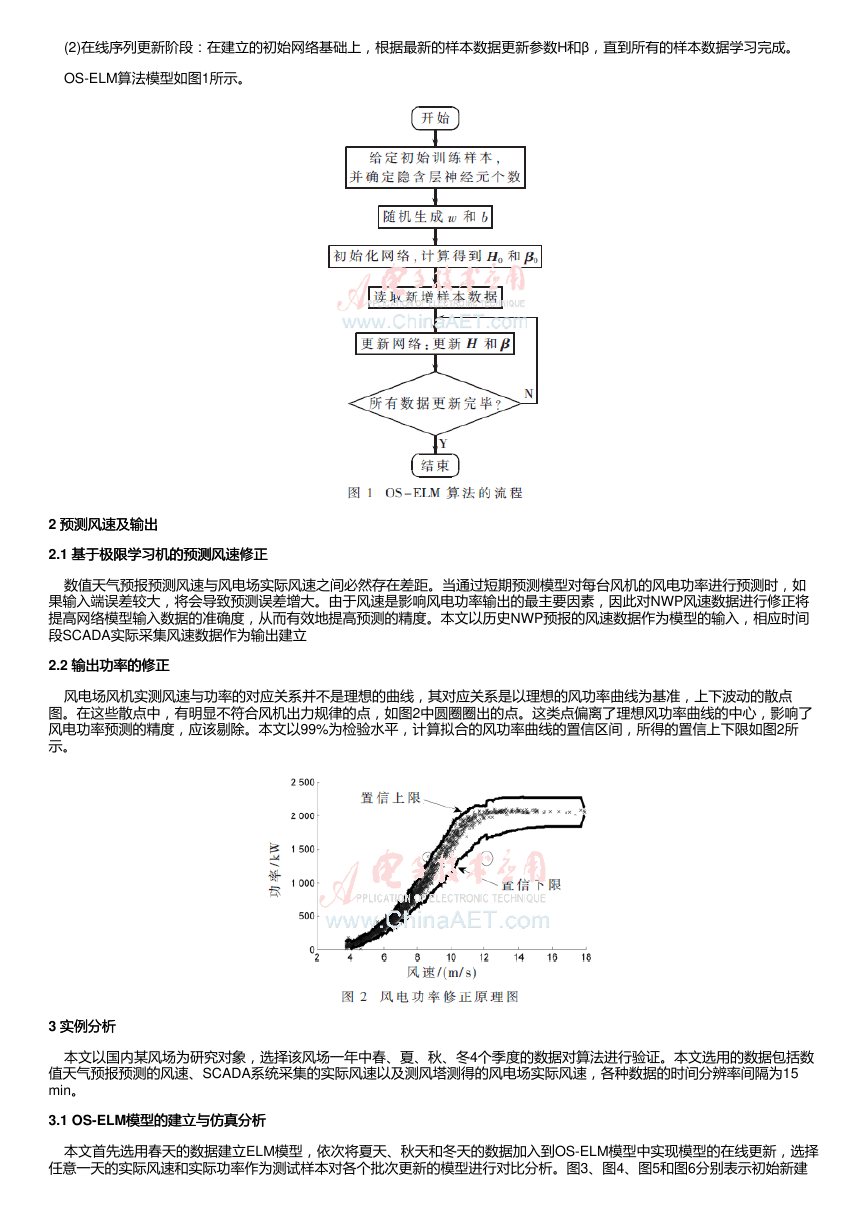
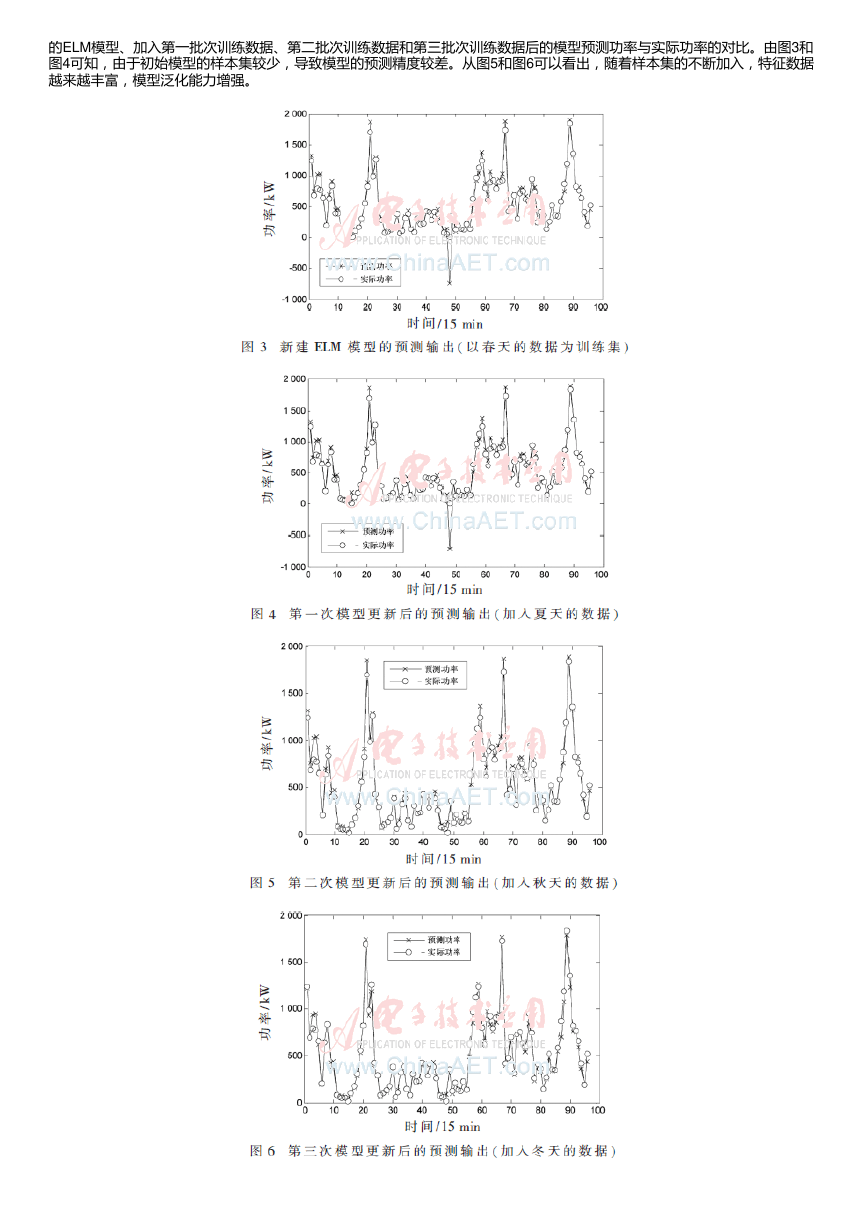
(2)在线序列更新阶段：在建立的初始网络基础上，根据最新的样本数据更新参数H和β，直到所有的样本数据学习完成。 OS-ELM算法模型如图1所示。 2 预测风速及输出预测风速及输出 2.1 基于极限学习机的预测风速修正基于极限学习机的预测风速修正数值天气预报预测风速与风电场实际风速之间必然存在差距。当通过短期预测模型对每台风机的风电功率进行预测时，如果输入端误差较大，将会导致预测误差增大。由于风速是影响风电功率输出的最主要因素，因此对NWP风速数据进行修正将提高网络模型输入数据的准确度，从而有效地提高预测的精度。本文以历史NWP预报的风速数据作为模型的输入，相应时间段SCADA实际采集风速数据作为输出建立 2.2 输出功率的修正输出功率的修正风电场风机实测风速与功率的对应关系并不是理想的曲线，其对应关系是以理想的风功率曲线为基准，上下波动的散点图。在这些散点中，有明显不符合风机出力规律的点，如图2中圆圈圈出的点。这类点偏离了理想风功率曲线的中心，影响了风电功率预测的精度，应该剔除。本文以99%为检验水平，计算拟合的风功率曲线的置信区间，所得的置信上下限如图2所示。 3 实例分析实例分析本文以国内某风场为研究对象，选择该风场一年中春、夏、秋、冬4个季度的数据对算法进行验证。本文选用的数据包括数值天气预报预测的风速、SCADA系统采集的实际风速以及测风塔测得的风电场实际风速，各种数据的时间分辨率间隔为15 min。 3.1 OS-ELM模型的建立与仿真分析模型的建立与仿真分析本文首先选用春天的数据建立ELM模型，依次将夏天、秋天和冬天的数据加入到OS-ELM模型中实现模型的在线更新，选择任意一天的实际风速和实际功率作为测试样本对各个批次更新的模型进行对比分析。图3、图4、图5和图6分别表示初始新建

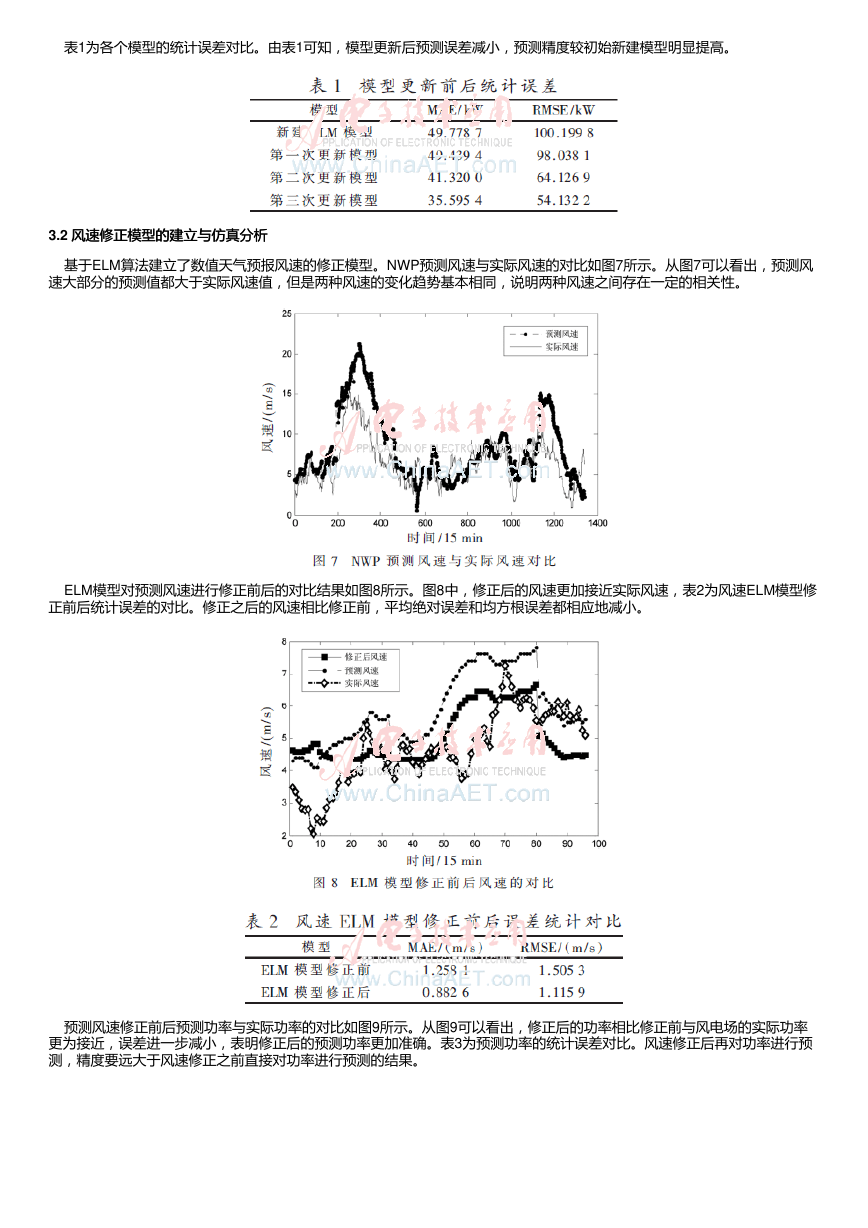
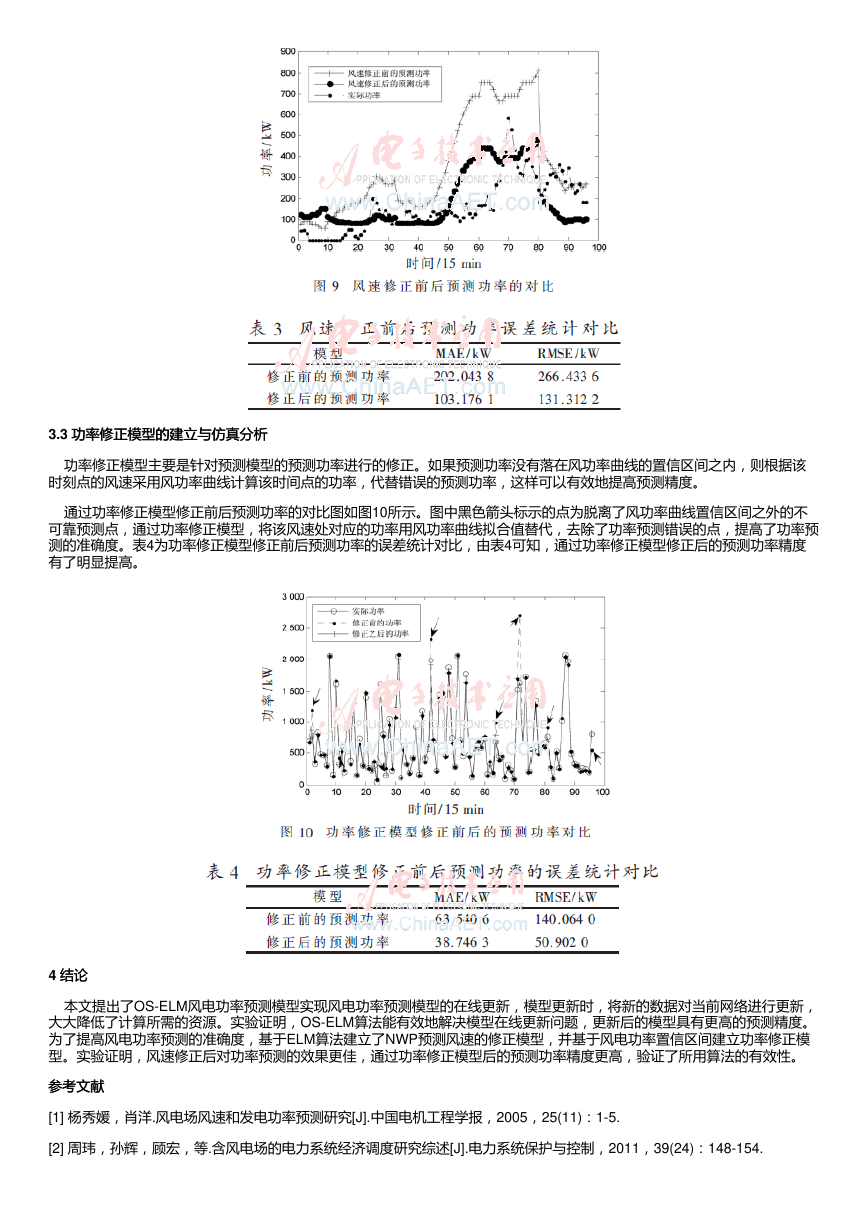
的ELM模型、加入第一批次训练数据、第二批次训练数据和第三批次训练数据后的模型预测功率与实际功率的对比。由图3和图4可知，由于初始模型的样本集较少，导致模型的预测精度较差。从图5和图6可以看出，随着样本集的不断加入，特征数据越来越丰富，模型泛化能力增强。

表1为各个模型的统计误差对比。由表1可知，模型更新后预测误差减小，预测精度较初始新建模型明显提高。 3.2 风速修正模型的建立与仿真分析风速修正模型的建立与仿真分析基于ELM算法建立了数值天气预报风速的修正模型。NWP预测风速与实际风速的对比如图7所示。从图7可以看出，预测风速大部分的预测值都大于实际风速值，但是两种风速的变化趋势基本相同，说明两种风速之间存在一定的相关性。 ELM模型对预测风速进行修正前后的对比结果如图8所示。图8中，修正后的风速更加接近实际风速，表2为风速ELM模型修正前后统计误差的对比。修正之后的风速相比修正前，平均绝对误差和均方根误差都相应地减小。预测风速修正前后预测功率与实际功率的对比如图9所示。从图9可以看出，修正后的功率相比修正前与风电场的实际功率更为接近，误差进一步减小，表明修正后的预测功率更加准确。表3为预测功率的统计误差对比。风速修正后再对功率进行预测，精度要远大于风速修正之前直接对功率进行预测的结果。

3.3 功率修正模型的建立与仿真分析功率修正模型的建立与仿真分析功率修正模型主要是针对预测模型的预测功率进行的修正。如果预测功率没有落在风功率曲线的置信区间之内，则根据该时刻点的风速采用风功率曲线计算该时间点的功率，代替错误的预测功率，这样可以有效地提高预测精度。通过功率修正模型修正前后预测功率的对比图如图10所示。图中黑色箭头标示的点为脱离了风功率曲线置信区间之外的不可靠预测点，通过功率修正模型，将该风速处对应的功率用风功率曲线拟合值替代，去除了功率预测错误的点，提高了功率预测的准确度。表4为功率修正模型修正前后预测功率的误差统计对比，由表4可知，通过功率修正模型修正后的预测功率精度有了明显提高。 4 结论结论本文提出了OS-ELM风电功率预测模型实现风电功率预测模型的在线更新，模型更新时，将新的数据对当前网络进行更新，大大降低了计算所需的资源。实验证明，OS-ELM算法能有效地解决模型在线更新问题，更新后的模型具有更高的预测精度。为了提高风电功率预测的准确度，基于ELM算法建立了NWP预测风速的修正模型，并基于风电功率置信区间建立功率修正模型。实验证明，风速修正后对功率预测的效果更佳，通过功率修正模型后的预测功率精度更高，验证了所用算法的有效性。参考文献参考文献 [1] 杨秀媛，肖洋.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25(11)：1-5. [2] 周玮，孙辉，顾宏，等.含风电场的电力系统经济调度研究综述[J].电力系统保护与控制，2011，39(24)：148-154.

[3] 张勇，肖建，迟永宁.基于机组调峰能力的电力系统风电接纳能力研究[J].太阳能学报，2014，3(6)：998-1003. [4] 张保会，李光辉，王进.风电接入电力系统故障电流的影响因素分析及对继电保护的影响[J].电力自动化设备， 2012，32(2)：1-8. [5] J.S.P.C，H.M.I.P，V.M.F.M.Short-term wind power forecasting in Portugal by neural networks and wavelet transform[J].Renewable Energy，2011(36)：1245-1251. [6] An Xueli，Jiang Dongxiang，Zhao Minghao，et al.Short-term prediction of wind power using EMD and chaotic theory[J].Nonlinear Science and Numerical Simulation，2012(17)：1036-1042. [7] 王韶，杨江平，李逢兵，等.基于经验模式分解和神经网络的短期风速组合预测[J].电力系统保护与控制，2012，40(10)：6- 11. [8] 刘纯，吕振华，黄越辉，等.长时间尺度风电出力时间序列建模新方法研究[J].电力系统保护与控制，2013，41(1)：7-13. [9] 武小梅，白银明，文福拴.基于RBF神经元网络的风电功率短期预测[J].电力系统保护与控制，2011，39(15)：80-83. [10] 叶小岭，刘波，邓华.基于小波分析和PSO优化神经网络的短期风电功率预测研究[J].可再生能源，2014，32(10)：1486- 1492. [11] 陆宁，武本令，刘颖.基于自适应粒子群优化的SVM模型在负荷预测中的应用[J].电力系统保护与控制，2011，39(15)： 43-47. [12] 马永杰，云文霞.遗传算法研究进展[J].计算机应用研究，2012，29(4)：1201-1206. [13] Xiao Dong，Wang Jichun，Mao Zhizhong.The research on the modeling method of batch process based on OS-ELM- RMPLS[J].Chemometrics and Intelligent Laboratory Systems，2014(134)：118-122.

资料库

基于OS-ELM的风速修正及短期风电功率预测.pdf

相关推荐

开发技术

热门标签

最新资料