logo资料库

主曲率均匀的网格光顺.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.48M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    2 第 27 卷 　第 1 期 2004 年 1 月 2 2 2 2 计 　　算 　　机 　　学 　　报 CHIN ESE J OU RNAL OF COMPU TERS Vol. 27 No. 1 Jan. 2004 　 主曲率均匀的网格光顺 刘胜兰 　周儒荣 　聂军洪 　周来水 (南京航空航天大学 CAD/ CAM 工程研究中心 　南京 210016) 摘 　要 　针对三角网格数据提出了一种主曲率均匀的光顺方法. 该算法首先通过建立局部抛物二次曲面来估算网 格顶点的主曲率和主方向 ,其次以邻点的主曲率和主方向的加权平均作为光顺后顶点的曲率值 ,然后由新曲率值 和二次曲面方程计算出调整后的顶点位置 ,实现模型的光顺. 进行局部光顺时 ,将区域内的点组成各个封闭环 ,根 据邻点所在环的层次分配权值 ,可以满足是否去除或保留内部区域特征的需要. 该文给出了应用实例 ,结果表明本 方法对网格模型实施整体和局部光顺均有较好的效果 ,光顺前后模型体积变化较小. 关键词 　网格光顺 ; 主曲率 ; 主方向 中图法分类号 TP391 Mesh Smoothing Using Principal Curvature Flow L IU Sheng Lan 　ZHOU Ru Rong 　N IE J un Hong 　ZHOU Lai Shui ( CA D/ CA M Engi neeri ng Research Center , N anji ng U niversity of Aeronautics & Ast ronautics , N anji ng 210016) be Abstract 　 A new algorit hm is presented for fairing arbitrary triangular meshes by inverse distance weighted average of principle curvature. Firstly , principal curvatures and principal directions are esti mated using local parabolic quadratic equations by weighted least square met hod. Then t he principal faired mesh is adopted as t he weighted average of neighbors’princi curvature of a vertex on t he to pal curvatures. The new curvatures can determine a new local parabolic quadratic equation. For satis fying t he new equation , every vertex should move towards its normal direction. Thus , t he new posi tions of vertices and a smoot hed mesh could be obtained. When fairing a specified local area , vertices are arranged on t he closed loops beforehand so t hat t he interior area can be well defeatured or feature retained by setting different weights for loops. In addition , some examples are provided to graphically demonstrate t hat t he presented algorit hm has volume preserved advantage and produces good results for fairing global or local mesh models. Keywords 　 mesh smoot hing ; principal curvature ; principal direction 1 　引 　言 在测量过程中 ,由于测量环境的振动和镜面反 射等因素 ,测量数据不可避免地存在测量噪声 ,去除 数据噪声的操作通常称为光顺. 对某一模型 ,如果只 需去除局部的噪声 ,我们称之为局部光顺. 测量数据 由离散的点构成 ,由于三角网格模型可描述测量点 01 08 08 ;修改稿收到日期 :2003 12. 本课题得到国家自然科学基金 (60273097) 、高等学校优秀青年教师教学科研奖励计 收稿日期 :2003 划和江苏省创新人才培养基金 (B K2001408) 资助.刘胜兰 ,女 ,1972 年生 ,讲师 ,博士研究生 ,从事 CAD/ CAM 、反求工程的研究. E mail : meeslliu @nuaa. edu. cn. 周儒荣 ,男 ,1935 年生 ,教授 ,博士生导师 ,主要研究领域为数字化设计与制造、反求工程. 聂军洪 ,男 ,1977 年生 , 博士研究生 ,从事反求工程方面的研究. 周来水 ,男 ,1962 年生 ,教授 ,博士生导师 ,主要研究领域为数字化设计与制造、反求工程、基于 Web 的 CAD/ CAM 等.
    08 计 　　算 　　机 　　学 　　报 2004 年 因此 ,本文提出了一种主曲率均匀的光顺方法 : 以邻点的主曲率和主方向的加权平均值作为光顺后 顶点的主曲率和主方向 ,由此确定顶点的调整量. Karbacher 是使顶点在各个方向的法曲率相等 ,光顺后 丢失了顶点的主方向信息 ,因而变形比本文方法大. 本文第 2 节计算网格上各顶点的主曲率和主方 向 ,第 3 节根据均匀后的主曲率和主方向计算顶点 在法矢上的位置调整 ,第 4 节给出一种局部区域的 光顺方法 ,第 5 节给出应用实例 ,第 6 节是结论. 2 　主曲率 、主方向计算 Milroy[ 9 ]通过在顶点处拟合一抛物二次曲面的 方法 ,实现对 OCS (Ort hogonal Cross Section Model) 模型的主曲率和主方向的计算. 该方法只要邻点数 目大于 3 个且邻点不共线就可实现 ,此条件在三角 网格模型中很容易满足. Milroy 在顶点处建立的二次曲面是 S ( u , v) = ( u , v , h ( u , v ) ) ,式中 h ( u , v ) = au2 + buv + cv 2 . 如图 1 所示 ,以 P 为原点 , h 轴为曲面在 P 点的法 矢 N 的方向 , u , v 相互正交且在 P 的切平面内 , ( Phuv) 坐标系由绝对坐标系 ( O xyz ) 经如下变换而 得 : O 平移至 P ,经旋转使得 z 轴与 h 轴重合 , 此时 u , v 可取 x , y 轴. T1 , T2是 P 点的两个主曲率对应 的主方向 ,在 P 点的切平面内 ,且相互正交. 局部坐标系的 h 轴依赖于 P 点的法矢 ,因此需 先估算出每一顶点的法矢. 如图 2 所示 , 设 V i是三 角网格上的一个顶点 , 有 m 个相邻三角片 Fj 和 m 之间的拓扑组织关系 ,因而作为测量数据的一种表 示方式在逆向工程中得到大量应用. 目前 ,对三角网格曲面的光顺研究主要从三个 方面展开 :最小能量法 、信号处理法和曲率均匀法. 最小能量法的原理是[ 1 ] :如果曲面在小扰度下的变 形能最小 ,曲面就最光顺. 参数多项式曲面 (如 B 样 条曲面) 的 光 顺 通 常 采 用 这 种 方 法. Kobbelt [ 2 ] 和 Welch[ 3 ]给出了三角网格离散模型下曲率的估算方 法 ,建立了能量方程并给出求解方法. 这种方法的主 要问题是能量最小化的求解过程复杂 、计算量大 、速 度慢. Taubin[ 4 ]用信号处理的方法将离散傅立叶变换 应用到三维数据点 ,曲面光顺问题就转化为信号的 低通滤波 ,由此来确定顶点沿拉普拉斯算子方向上 的调整. 由于拉普拉斯算子是一个线性算子 ,因而该 方法计算简单 、速度快 ,得到大量应用 ,该方法也被 称作拉普拉斯光顺法. Kobbelt [ 5 ]也舍弃了最小能量 法 ,采用这种方法对多分辨率网格模型进行光顺 ; Desbrun[ 6 ]用隐函数方法实现了网格的拉普拉斯调 整. 信号处理方法的关键问题是如何选取合适的参 数来合理区分低通信号和噪声. 主要问题是会使曲 率大的局部收缩过快 ,而曲率小的部位又得不到补 偿 ,曲面容易产生不希望的变形 ,Desbrun[ 6 ] 、刘新 国[ 7 ]加入体积保持约束来抑制模型的过度收缩. 曲率均匀法的目标是减少网格顶点间的曲率变 化 ,以平均后的曲率与原曲率之间的差值来确定顶 点的调整量. 计算曲率的方法很多 ,但往往并不能由 该方法反算出顶点位置 ,因而曲率均匀法的研究并 不多见. Karbacher[ 8 ] 在顶点和邻点之间拟合一圆 弧 ,圆弧半径就是顶点在该方向上的法曲率半径 ,调 整目标是使顶点在各个方向上的法曲率趋于该点的 平均曲率值 ,实现了测量数据的光顺. 该方法计算速 度很快 ,但容易使网格曲面在各处趋于球面. 本文算 法的基本思想是主曲率均匀 ,它在体积保持和局部 光顺时的边界光滑等方面比 Karbacher 方法有明显 的优点. 曲面上的某一点处沿不同的方向有不同的法曲 率 ,其中最大和最小的法曲率就是该点的主曲率 ,对 应的方向是主方向. 如果曲面上有一条特征线 ,线上 某点的主方向之一与特征线的走向相同. 由欧拉公 式[ 1 ]可知 :如果曲面上某两点的主曲率和主方向相 等 ,则该两点在任意方向上的法曲率均相等. 可以推 论出 :如果主曲率均匀变化 ,则各个方向上的法曲率 也均匀变化 ,平均曲率也均匀变化.
    个相邻顶点 V j , nj是相邻的三角片 Fj的单位法矢 , d i , j是顶点 V i 与邻点 V j 的长度 , d j , j + 1是邻点 V j + 1的长度. 由文献[10 ] ,顶点 V i的法矢 N i为 与 V j N i = ∑ ·nj , dj , j +1 m j = 1 d i , j + d i , j 其中 di , m +1 + d j , j +1 = di ,1 +1 (1) 获得法矢 Ni后 ,顶点 V i处的局部坐标系 ( Phuv) 就可建立 ,邻点 V j ( x j , y j , z j) 在该局部坐标下的坐 标值为 ( uj , v j , hj) . 二次曲面就可由邻点的局部坐标 用最小二乘法来拟合 ,在所有的邻点 V j中 , 靠近 V i 的邻点更能体现 V i点曲面的局部形状 ,因此我们根 据顶点与邻点的距离给邻点分配权值 w j , 就可得到 加权最小二乘意义下的二次曲面. V j与曲面 S ( u , v) 之间的加权最小二乘误差函数为 m Q = ∑ j = 1 u j v j au2 j + bujv j + cv 2 j - uj v j hj 2 ·w j 18 ( a - c) 2 + b2 T 1 = (1 ,λ1) = b , c - a - T 2 = (1 ,λ2) = c - a - ( a - c) 2 + b2 , - b (6) 当 b = 0 时 ,曲面 S ( u , v ) 是一椭球面 , 主方向 在 u , v 轴上. 当 a < c 时 , T1 在 u 轴上 , 当 a > c 时 , T1在 v 轴上 , 当 a = c 时 , 椭球面就退化为球 面 ,主方向可以是任意值 ,我们规定它为 (0 ,0) . 有 若 a < c ,则 T1 = (1 ,0) T2 = (0 ,1) ;若 a > c ,则 T1 = (0 ,1) T2 = (1 ,0) ; 若 a = c ,则 T1 = (0 ,0) T2 = (0 ,0) . 由公式 k = L + 2 Mλ+ Nλ2 E + 2 Fλ+ Gλ2 ,可得 V i点的主曲率为 k1 = a + c - ( a - c) 2 + b2 k2 = a + c + ( a - c) 2 + b2 (7) 1 期 刘胜兰等 :主曲率均匀的网格光顺 3 　顶点位置调整 (2) 则 m j = 1 j m . = 0 和 Q b j a + ∑w j u3 = 0 ,可得到 j v j b + ∑w j u2 其中权值 w j = e - dj/ max ( dj ) ,1 均简写为 ∑. 要使 Q 最小 , 在以下叙述中 , ∑ Q Q = 0 , a c ∑w j u4 　　 ∑w j u2 j hj ∑w j u3 　　 ∑w j ujv j hj ∑w j u2 　　 ∑w j v 2 j hj j a + ∑w j u jv 3 j v j a + ∑w j u2 j b + ∑w j uj v 3 j b + ∑w jv 4 j c = j c = j c = j v 2 j v 2 j v 2 (3) 解线性方程组 (3) , 得到曲面 S ( u , v ) 的参数 a , b 和 c. V i点的主曲率记为 k1 , k2 ,主方向记为 T1 , T2 , 曲面 S ( u , v) 在 u = 0 , v = 0 处的主曲率 、主方向就 是网格顶点 V i的主曲率 、主方向. 由曲面的第一 、第 二基本公式可知 , 主方向的方位 λ= d v/ d u 是方程 ( GM - FN )λ2 + ( GL - EN )λ+ ( FL - EM ) = 0 的 根 ,对曲面 S ( u , v) ,当 u = 0 , v = 0 时 ,有 bλ2 + 2 ( a - c)λ - b = 1 当 b ≠0 时 ,解方程 (4) ,可得 c - a - λ1 = ( a - c) 2 + b2 b ( a - c) 2 + b2 b 因此当 b ≠0 时 ,主方向为 c - a + λ2 = (4) (5) 本文提出的主曲率均匀光顺法中 , 顶点位置的 调整是根据均匀后顶点的主曲率和主方向来确定 的 ,因此需计算均匀后的主曲率和主方向. 我们先计 算主方向 , 由于 T1 , T2相互垂直 , 实际只需考虑主 方向 T1即可. 以 T1与 u 轴的夹角θ(即 arctgλ1) 来 描述顶点 V i 的主方向 , 对邻点 V j ,θj 是 T1 ( V j ) 在 V i的局部坐标平面 uv 上的投影与 u 轴之间的夹 角 ,如果 T1 ( V j) 为 (0 , 0) ,表明 V j的主方向不确定 , 此时令 θj =θ. 根据加权平均可获得均匀后的主方 向θ′. 均匀后的主曲率就是邻点 V j在θ′方向及 (θ′+ π/ 2) 方向上的法曲率的加权平均 ,设 V j的主曲率分 别记做 k1 j , k2 j , V j 在该方向上的法曲率可以根据 欧拉公式来计算 , 权值 w j的计算同式 (2) . 因此 , 得 到 V i点调整后的主方向θ′,主曲率 k′1, k′2分别为 / ∑w j θ′= ∑θj w j k′1= ∑ k1 jcos2 (θj - θ′) + 　k2 jsin2 (θj - θ′) w j k′2= ∑ k1 jsin2 (θj - θ′) + 　k2 jcos2 (θj - θ′) w j / ∑w j / ∑w j (8) 在式 (5) 和式 (7) 中 , 如果 k1 , k2 ,λ1是已知数 , 由 3 个方程也可以解出变量 a , b , c. 主曲率均匀后 可确定一个新的曲面 , 将式 (8) 的结果代入式 (5) , (7) 中 ,则解出曲面参数 a′, b′和 c′为 a′= ( k′1+ k′2λ′2 1) / ( (1 + λ′2 b′= λ′1( k′1- k′2) / (1 + λ′2 1) / ( (1 +λ′2 c′= ( k′2+ k′1λ′2 1) / 2) 1) 1) / 2) (9)
    28 计 　　算 　　机 　　学 　　报 2004 年 loop) 可从大到小分配 ,例如本算法中常采 (记作 w 用的一种分配方案是 1 ,0. 5 ,0. 0. 在进行局部光顺时 , 用 w loop ×w j取代式 (9) 中的 w j ,可以更多地去除 内部特征 ,选定区域与外部形状更协调一致. 其中 ,λ′1= tg (θ′) , V i的局部坐标为 (0 , 0 , 0) , 仍然在 新曲面上 ,而邻点 V j与新曲面在 h 轴上存在偏差 , 记为Δh ( V j) : Δh ( V j) = a′u2 j - hj j + b′ujv j + c′v 2 (10) 要使得 V i 的主曲率均匀 , 每个邻点 V j 需在 h 轴上移动Δh ( V j ) 距离. 如果我们让 V j保持位置不 动 ,而让新曲面在 h 轴上有一个相反的位移也可满足 要求 ,此时 V i与移动后的曲面在 h 轴上就有偏差. 由 于调整是在所有顶点上进行的 ,因此光顺时 V i只需移 动偏差的一半位移即可. V i在 h 轴上的调整位移δ为 (11) δ = - ∑w jΔh ( V j) / 2 ∑w j 根据实际需要 ,调整操作可迭代数次. 4 　局部光顺 对于选定区域的局部光顺 , 我们希望选定区域 与外围区域曲率协调一致 , 而不只是内部区域的曲 率相一致 ,因此外围邻点比内部邻点的作用大 ,应该 分配更大的权值. 对网格模型上的一个选定区域 ,其 边界上的顶点由三角片的边连接成一封闭环. 若去掉 边界上的顶点及与顶点相邻的三角片 ,剩余网格构成 的区域也有一个边界 ,也可以得到一个封闭环. 因此 , 由边界向内 ,区域内的点可连接成一系列的封闭环 , 环的层次 ( loop) 分别为 0 , 1 , …, n ,且环与环之间没 有交点 ,如图 3 所示. 当 loop ( V j) < loop ( V i) 时 ,称 V j在 V i的环外 ;当 loop ( V j) = loop ( V i) 时 ,称 V j在 V i的 环 上 ; 当 loop ( V j ) > loop ( V i ) 时 , 称 V j 在 V i 的环内. 当邻点分别在环外 、环上和环内时 ,权值 5 　应用实例 应用本文算法 , 作者在 1. 5 GHz 的 Pentium IV 计算机上对若干网格模型进行了光顺操作 ,所有模 型均在 flat shading 模式下显示 ,并比较了光顺前后 模型的体积变化. 体积变化可以在一定程度上作为 模型变形的量化体现 ,本文采用 Desbrun[6 ] 的方法 来计算网格体积 :从空间任取一点 (如原点) ,各三角 片与该点形成的有向棱锥体的体积之和. 图 4 是一兔子模型 , 有顶点 7347 个 、三角片 14690 个 ,其中图 (a) 为光顺前模型 ,图 (b) 为光顺 5 次的结果 ,图 (c) 为光顺 200 次的结果 ,图 (d) 为 Kar bacher 算法光顺 5 次的结果 , 图 (e) 为 Karbacher 算 法光顺 10 次的结果. 图 5 是一圆环模型 , 有顶点 1800 个 、三角片 3600 个 ,其中图 5 (a) 为光顺前模型 ,图 (b) 为光顺 5 次的结果 ,图 (c) 为光顺 200 次的结果 ,图 (d) 为 Kar bacher 算法光顺 5 次的结果 , 图 (e) 为 Karbacher 算 法光顺 100 次的结果.
    2 2 2 1 期 刘胜兰等 :主曲率均匀的网格光顺 38 由图 4 ,图 5 可以看出 ,本算法对网格模型中的 噪声有较好的去除效果. 在迭代次数较少时 , Kar bacher 算法的光顺效果稍好 ;随着迭代次数的增加 , 本算法对形状剧烈变化的区域 (如兔子耳朵处) 有较 好的收敛性 , 而 Karbacher 算法在该区域容易引起 发散 ;本算法会使模型保持原有的凹凸 ,而不是趋于 平坦. 表 1 中对比了模型的光顺时间和光顺前后的 体积变化 ,可以看出 ,本算法复杂度较高 , 但比 Kar bacher 算法能更好地保持模型的体积. 因此 ,本算法 与信号处理方法相比 ,能避免模型的过度收缩. 表 1 　光顺时间及体积的对比 模型 初始 体积 光顺一次 时间 (s) 本文算法 光顺 5 次 体积 体积 变化 ( %) 光顺 200 次 体积 变化 ( %) 体积 光顺一次 时间 (s) Karbacher 算法 光顺 5 次 体积 体积 变化 ( %) 光顺 100 次 体积 体积 变化 ( %) 兔子 1. 484 E4 圆环 1. 012 E6 1. 90 0. 47 1. 488 E4 1. 015 E6 0. 29 0. 30 1. 501 E4 1. 073 E6 1. 12 6. 03 0. 57 0. 14 1. 388 E4 1. 078 E6 6. 50 6. 12 - - 2. 118 E6 109. 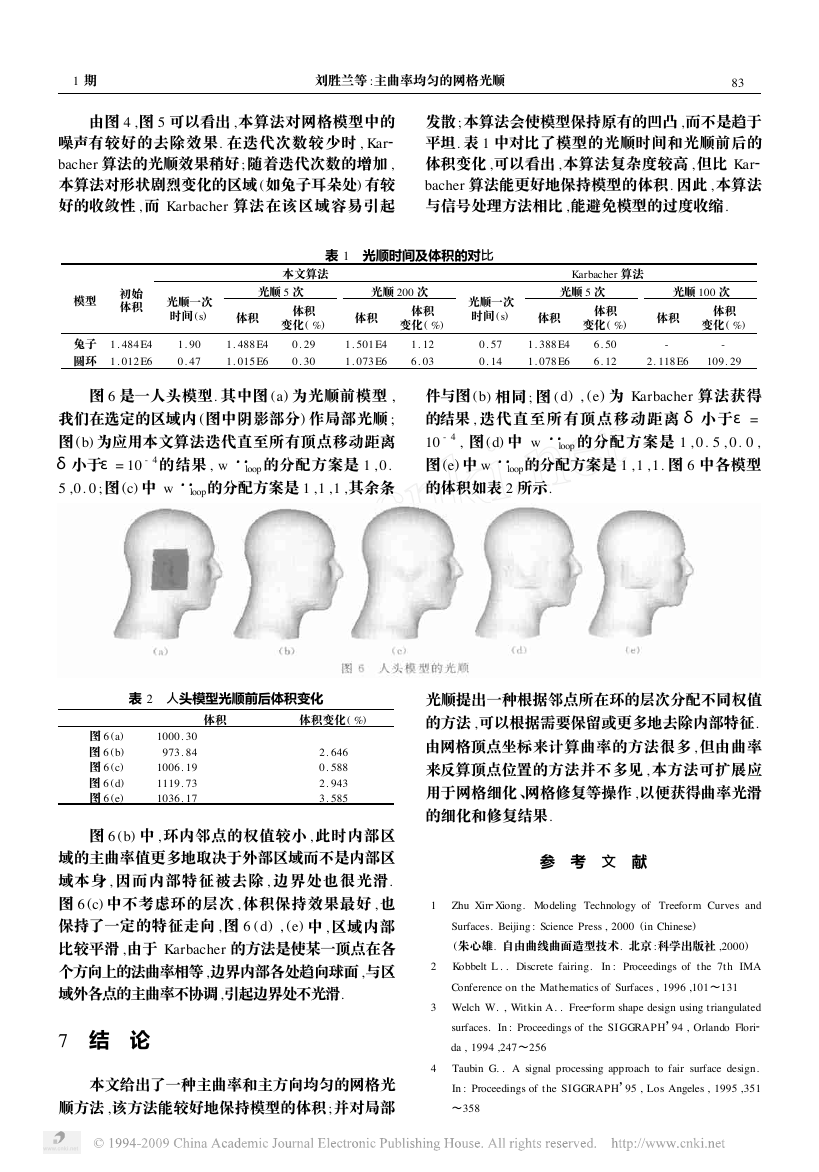29 图 6 是一人头模型. 其中图 (a) 为光顺前模型 , 我们在选定的区域内 (图中阴影部分) 作局部光顺 ; 图 (b) 为应用本文算法迭代直至所有顶点移动距离 δ小于ε= 10 - 4的结果 , w loop 的分配方案是 1 , 0. loop的分配方案是 1 ,1 ,1 ,其余条 5 ,0. 0 ;图 (c) 中 w 件与图 (b) 相同 ; 图 ( d) , (e) 为 Karbacher 算法获得 的结果 , 迭代直至所有顶点移动距离 δ 小于ε= 10 - 4 , 图 (d) 中 w loop 的分配方案是 1 , 0. 5 , 0. 0 , 图 (e) 中 w loop的分配方案是 1 , 1 , 1. 图 6 中各模型 的体积如表 2 所示. 表 2 　人头模型光顺前后体积变化 体积 体积变化 ( %) 图 6 (a) 图 6 (b) 图 6 (c) 图 6 (d) 图 6 (e) 1000. 30 973. 84 1006. 19 1119. 73 1036. 17 2. 646 0. 588 2. 943 3. 585 光顺提出一种根据邻点所在环的层次分配不同权值 的方法 ,可以根据需要保留或更多地去除内部特征. 由网格顶点坐标来计算曲率的方法很多 , 但由曲率 来反算顶点位置的方法并不多见 , 本方法可扩展应 用于网格细化 、网格修复等操作 ,以便获得曲率光滑 的细化和修复结果. 图 6 (b) 中 , 环内邻点的权值较小 , 此时内部区 域的主曲率值更多地取决于外部区域而不是内部区 域本身 , 因而内部特征被去除 , 边界处也很光滑. 图 6 (c) 中不考虑环的层次 , 体积保持效果最好 , 也 保持了一定的特征走向 , 图 6 ( d) , (e) 中 , 区域内部 比较平滑 ,由于 Karbacher 的方法是使某一顶点在各 个方向上的法曲率相等 ,边界内部各处趋向球面 ,与区 域外各点的主曲率不协调 ,引起边界处不光滑. 7 　结 　论 本文给出了一种主曲率和主方向均匀的网格光 顺方法 ,该方法能较好地保持模型的体积 ;并对局部 参 考 文 献 1 Zhu Xin Xiong. Modeling Technology of Treeform Curves and Surfaces. Beijing : Science Press , 2000 (in Chinese) (朱心雄. 自由曲线曲面造型技术. 北京 :科学出版社 ,2000) 2 Kobbelt L . . Discrete fairing. Conference on the Mathematics of Surfaces , 1996 ,101～131 In : Proceedings of the 7th IMA 3 Welch W. , Witkin A. . Free form shape design using triangulated surfaces. In : Proceedings of the SIGGRAPH’94 , Orlando Flori da , 1994 ,247～256 4 Taubin G. . A signal processing approach to fair surface design. In : Proceedings of the SIGGRAPH’95 , Los Angeles , 1995 ,351 ～358
    48 计 　　算 　　机 　　学 　　报 2004 年 5 Kobbelt L . , Campagna S. , Vorsatz J . , Seidel H. P. . Interactive smoothing of scattered 3D data. In : Ellson R. N. , Nurre J . H. resolution modeling on arbitrary meshes. In : Proceedings of multi the SIGGRAPH’98 , Orlando Florida , 1998 ,105～114 Dimensional Image Capture and Applications , Wash eds. Three ington : SPIE Press , 1998 ,168～177 6 Desbrun M. , Meyer M. , Schroder P. , Barr A. . Implicit fairing 9 Milroy M. J . , Bradley C. , Vickers G. W. . Segmentation of a 7 8 of irregular meshes using diffusion and curvature flow. In : Pro ceedings of the SIGGRAPH’99 , Los Angeles , 1999 ,317～324 Liu Xin Gann , Peng Qun J un , Heng Phen Guo , Bao Hu Sheng. 10 around model using an active contour. Computer Aided De wrap signed , 1997 , 29 (4) : 299～320 Ke Ying Lin. Geometric Modeling for Three Dimensional Scat Volume preserved multiresolution mesh modeling. Chinese Journal of Computers , 2000 ,23 (9) : 905～910 (in Chinese) (刘新国 , 鲍虎军 , 王平安 , 彭群生. 体积保持的多分辨率多边 形网格的光顺造型. 计算机学报 ,2000 ,23 (9) : 905～910) Karbacher S. , Hausler G. . A new approach for modeling and tered Data and Its Application[ Ph. D. dissertation ] . Nanjing Uni versity of Aeronautics & Astronautics , Nanjing , 1992 ( in Chi nese) (柯映林. 离散数据的几何造型技术及其应用研究 [ 博士学位 论文 ] . 南京航空航天大学 ,南京 , 1992) L IU Sheng Lan , born in 1972 , lec turer and Ph. D. candidate. Her main re search interests include CAD/ CAM and reverse engineering. visor. His research interests include digital design & manufac ture and reverse engineering. NIE Jun Hong , Ph. D. candidate. His main research in terests include CAD/ CAM and reverse engineering. ZHOU Lai Shui , professor , Ph. D. supervisor. His re search interests include digital design & manufacture , reverse engineering and Web based CAD/ CAM. ZHOU Ru Rong , born in 1935 , professor , Ph. D. super Background This paper reports two project . “Computer Solution of the Dimensional Jigsaw Puzzles and It’s Application”aims at Multi developing geometric methods for automatic shape recognition and matching from measured data. Another projects “ Key Technology of Innovation Design Based on Virtual Digital Sam ples”aims at proposing a systematic scheme and developing nec essary technologies to reconstruct a CAD model from“Virtual Digital Samples”such as scattered point clouds , mesh models etc. Some work such as data simplification , triangular mesh model reconstruction from cloud data and piecewise B spline sur faces fitting over arbitrary triangle meshes has been accom plished. This work is proposed for smoothing the globe and local arbitrary triangle meshes obtained from measure equipments.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料