logo资料库

隔震支座力学模型对隔震分析的影响.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.53M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 隔震支座力学模型对隔震分析的影响# 袁涌，李林* （华中科技大学土木工程与力学学院，武汉，430074） 5 摘要：随着近年来地震工程的发展，基础隔震结构的应用越来越广泛，而铅芯隔震橡胶支座 以其突出的优点更是运用十分广泛。铅芯隔震橡胶支座的力学模型通常采用双线性力学模型 进行模拟，而实际上支座发生大变形时，其滞回曲线呈现三线性的形态，本文就此提出确定 三线性力学模型参数的计算方法，并通过 ANSYS 分析软件对采用不同力学模型进行的建筑 隔震分析结果做了对比，对比研究表明多遇地震下分析结果相差很小，罕遇地震下分析结果 差别较大。 关键词：隔震分析 铅芯隔震橡胶支座 力学模型 三线性力学模型 双线性力学模型 中图分类号：TU312 10 15 the Study on the isolation analysis result depending on the isolation bearing mechanics model Yuan Yong, Li Lin (College of civil engineering and mechanics, Huazhong University of Science and Technology,Wuhan,430074) 20 25 30 Abstract: With the development of earthquake engineering in recently years, the application of base isolation structure is more and more widely. Because of the prominent advantage of lead- rubber isolation bearings, it is widely used in this range. The mechanical model of lead- rubber isolation bearings usually use bilinear hysteretic model, but the actual hysteretic behaviors under major earthquake presents tri-linear perform. So it is necessary to consider the impact of differences of the large deformation bearing mechanics model for isolation analysis. In order to correctly utilize the analysis model, basing on the theory study, the mechanical parameters of the tri-linear model of isolation bearing was studied. The different dynamic response of two kind of isolated structures which is used bilinear model and tri-linear model of lead rubber bearings was also discussed. Key words: Isolation analysis; Lead-rubber isolation bearings; Mechanical model; Tri-linear mechanical model; Bilinear mechanical model 0 引言 隔震结构在当下地震多发期内所表现出的良好性能使得其对传统的抗震设计带来巨大 35 的挑战[1]。隔震支座具有良好的水平变形能力，设置在结构中能显著增大结构的自振周期， 减小其层剪力和层位移，吸收地震能量，使上部结构不会发生严重的破坏[2]。现阶段，无铅 芯隔震橡胶支座在隔震分析时所采用的力学模型通常为等效线性力学模型,铅芯隔震橡胶支 座通常采用双线性滞回模型[3,4]。但是在对铅芯隔震橡胶支座进行大量试验后发现，铅芯隔 震橡胶支座在大变形条件下，橡胶层会出现明显的硬化现象，其滞回曲线不再表现为双线性 40 力学特性，而呈现“三线性”的力学形态[5]，而如今在隔震分析中并未考虑大变形下支座力 学模型差异所带来的影响，均采用等效线性或者双线性力学模型，特别是在大震作用下分析 结果存在误差。因此需要在分析中考虑支座的大变形硬化作用，采用三线性力学模型。而三 线性力学模型的力学参数如何确定？三线性和双线性力学模型在隔震结构中对结构的隔震 基金项目：国家自然科学基金(51278219)，教育部博士点基金(20090142120075) 作者简介：袁涌(1976 年 2 月)，男，副教授，主要研究方向：结构减隔震控制与实验技术. E-mail: yuanyonghuagong@gmail.com - 1 -
    中国科技论文在线 http://www.paper.edu.cn 分析结果有怎样的影响？这是本论文主要讨论的两个问题。本文旨在寻求确定三线性力学模 45 型力学参数的计算方法，并利用结构分析软件分析具体隔震结构的隔震支座采用不同的力学 模型时其隔震分析结果的差异性，对当今隔震分析结果的可靠性进行了研究。 1 支座力学模型参数的确定 1.1 双线性力学模型 铅芯隔震橡胶支座的水平刚度及简化力学模型通常是根据试验的具体曲线拟合而成，常 50 用的双线性力学模型就是应用最小二乘法原理将试验所得滞回曲线数据进行拟合而得出具 体的力学参数，实际上就是利用最小二乘法原理确定两条直线和试验曲线拟合[6]。原理如下： 已知各数据点（xi，yi）（i=1,2,„,n），拟确定的直线方程为 Y=a+bX，其中 a，b 为待定系 数，根据最小二乘法原理，计算值 yj（=a+bxi）与实测值 yi 误差的平方和 最 小为优化判据，令 ，要使其最小，则只需对 a，b 求偏导数并令其等 55 于零，即可求解 a，b。 （1.1） （1.2） 整理上面两个式子可得到： 60 （1.3） 求出 a，b 之后，就可以确定双线型滞回曲线，如图 1 所示，其中 K1 为屈服前刚度，K2 为 屈服后刚度，Fy 和 uy 为屈服力和屈服位移，Fm 和 um 为最大水平力和最大位移。 65 1.2 三线性力学模型 图 1 双线性力学模型 Fig.1 Bilinear mechanical model 当把实际的试验滞回曲线模拟成三线性滞回曲线（如图 2）时，不再采用最小二乘法原 理，本研究主要根据支座等效阻尼比不变的原则来确定[7]，支座的等效阻尼比可表示为： （1.4） - 2 - 2()iiabxy2(,)()iiababxy2()2()0iiiiabxynabxya22()2()0iiiiiiixabxyaxbxxyb（）()/(1)iiiiiaxyxynx()/iibynax4eqWW
    中国科技论文在线 http://www.paper.edu.cn 70 其中， 为等效阻尼比， 为滞回环的面积， 为最大应变能。 图 2 三线性力学模型 Fig.2 Tri-linear mechanical model 由此，可提出以下假设： 75 （1）曲线的屈服前刚度和最大位移点不变； （2）屈服后，试验滞回曲线与三线性力学模型所包围的面积（假设试验曲线在上方时 面积为正，如图 2 所示，A1 为正值，A2 为负值）之和为零，即 A1+A2=0； （3）假定试验滞回曲线与简化三线性力学模型滞回环的面积相等，这是为了保证支座 的等效阻尼比保持不变。 80 屈服前刚度 K1 与双线性力学模型的确定方法一致，那么屈服点（ ， ）已知，最 大位移点（ ， ）也已知，唯一需要确定的是强化位移点的坐标（ ， ），根据假 设（1）和（2）可以列出两个方程求解 和 。 85 90 图 3 三线性力学模型计算图 Fig.3 Calculation of tri-linear mechanical model 根据假设（1），要使 A1+A2=0，则只需满足试验曲线与横轴所围的面积与三线性力学模 型（ ， ）段与横轴所围的面积相等即可，通过曲线面积积分，可以把试验所得第三圈 滞回曲线滞回环的面积 A0 求出来，这里不再详述，根据图 3 可以求出三线性力学模型（ ， ）段与横轴所围的面积，可列出方程一： （1.5） 根据假设（2），设试验滞回曲线滞回环面积为 A，要使模拟的滞回曲线滞回环面积不 变，则必须求出三线性力学模型滞回环的面积，如图 5 所示，滞回环的面积可表示为 4SOabc+2S - 3 - eqW(/2)mmWFuyuyFmumFpupFpupFyumuyumu011()()()()22ypypmpmpFFuuFFuuA
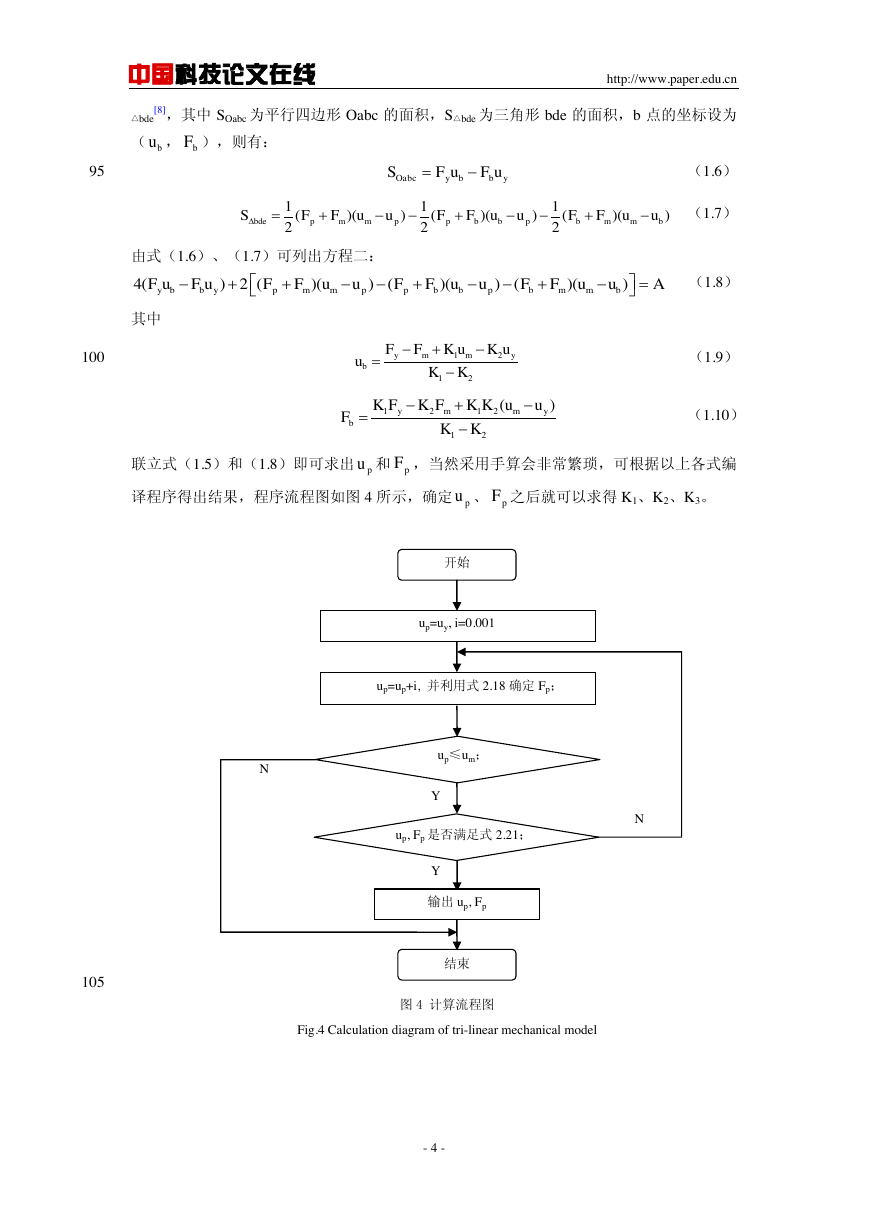
    中国科技论文在线 http://www.paper.edu.cn [8]，其中 SOabc 为平行四边形 Oabc 的面积，S△bde 为三角形 bde 的面积，b 点的坐标设为 △bde （ ， ），则有： 95 （1.6） 由式（1.6）、（1.7）可列出方程二： 其中 100 （1.7） （1.8） （1.9） （1.10） 联立式（1.5）和（1.8）即可求出 和 ，当然采用手算会非常繁琐，可根据以上各式编 译程序得出结果，程序流程图如图 4 所示，确定 、 之后就可以求得 K1、K2、K3。 开始 up=uy, i=0.001 up=up+i, 并利用式 2.18 确定 Fp； N up≤um； Y up, Fp 是否满足式 2.21； N Y 输出 up, Fp 结束 图 4 计算流程图 Fig.4 Calculation diagram of tri-linear mechanical model 105 - 4 - bubFOabcybbySFuFu111()()()()()()222bdepmmppbbpbmmbSFFuuFFuuFFuu4()2()()()()()()ybbypmmppbbpbmmbFuFuFFuuFFuuFFuuA1212ymmybFFKuKuuKK121212()ymmybKFKFKKuuFKKpupFpupF
    中国科技论文在线 http://www.paper.edu.cn 110 Fig.5 Curve area calculation of tri-linear mechanical model 图 5 三线性力学模型曲线面积求解图 2 隔震分析结果对比研究 为明确不同的隔震支座力学模型对隔震分析结果的影响，本文将对实际工程进行模拟分 析，分别采用双线性力学模型和三线性力学模型对铅芯隔震橡胶支座进行模拟，对采用两种 不同模型的结构在地震作用下的时程分析结果进行对比分析，研究其差异性的大小，从而评 115 估现阶段隔震设计的有效性和合理性。 所采用的实际模型为某保险中心大楼，采用钢筋混凝土框架结构形式，结构体型规则， 平面尺寸 81.7m×51.65m，共四层，除第一层层高 3m 外，其余各层均为 6m。该建筑的设防 烈度为 8 度，设计基本地震加速度值 0.20g，设计地震分组为第三组，II 类场地。 采用的隔 震方案为在底层外围柱下布置铅芯隔震支座 GZY4Q 920x231，中部柱下布置普通隔震橡胶支 120 座 GZY 1120x246。 图 6 分析模型图 Fig.6 Analysis model 经验算，该隔震结构所选择的隔震方案能起到良好的隔震效果，满足规范中关于支座竖 125 向压力、抗倾覆、水平最大位移限值及上部结构层剪力、层间位移和层间位移角限值的规定 [9]。该隔震结构的第一自振周期可延长到非隔震结构的 2 倍，使结构远离地震的卓越周期， 对降低上部结构的地震响应有利。根据以上的隔震方案采用 ANSYS 对该结构进行有限元分 析（模型如图 6），采用梁单元 BEAM188 模拟梁柱构件，用 SHELL63 单元模拟楼板，对 于活荷载和墙体自重的输入，将其简化为梁柱节点上的集中质量，利用质量单元 MASS21 进行模拟，隔震支座采用 COMBIN39 单元进行模拟[10]，其力学参数如下（注：括号中的数 130 - 5 -
    中国科技论文在线 http://www.paper.edu.cn 表示罕遇地震下的参数）：普通支座：等效水平刚度 Kq=4（4）kN/mm。铅芯支座：双线 性力学模型：K1=20.9（29）kN/mm； K2=1.9（2.6）kN/mm；等效水平刚度 Kq=5（3.9）kN/mm； Fy=323kN。三线性力学模型：K1=20.9（29）kN/mm； K2=1（1.45）kN/mm； K3=0（10.9） kN/mm；Kq=5（3.9）kN/mm；Fy=323kN；up=220mm。 135 选用 EL central 波、TAFT 波和人工波对该结构在多遇和罕遇地震作用下的时程响应进 行分析，分别对支座水平位移，上部结构层剪力、层间位移和层间位移角进行对比分析。通 过对比发现，在多遇地震下，隔震分析结果相差很小，均在 1%以内，可见多遇地震下，铅 芯隔震支座无论采用双线性力学模型还是三线性力学模型，影响不大。下面将主要讨论罕遇 地震作用下的差异性。 140 通过分析可知，罕遇地震作用下，采用三线性力学模型的支座水平位移将变大（如图 7、 8），以 X 向为例，双线性力学模型的支座位移最大值分别为 216.5mm、182.3mm、204.1mm， 三线性力学模型的支座位移最大值分别为 225.7mm、198.1mm、214.4mm，其差值比率分别 为 4.249%、8.667%和 5.047%，可见支座最大位移不能超过后期强化位移时，差异性更大； 超过后期强化位移越多，差异性将越来越小。 145 (a) 双线性力学模型 (b) 三线性力学模型 (a) Bilinear mechanical model (b) Tri-linear mechanical model 图 7 罕遇地震作用下隔震支座的滞回曲线 Fig.7 Hysteresis curve of isolation bearing under severe earthquake 150 (a) X 向 (b) Y 向 (a) X-direction (b) Y-direction 图 8 罕遇地震作用下支座水平位移最大值对比 Fig.8 Maxi-horizontal displacement comparison of the isolation bearing under severe earthquake - 6 -
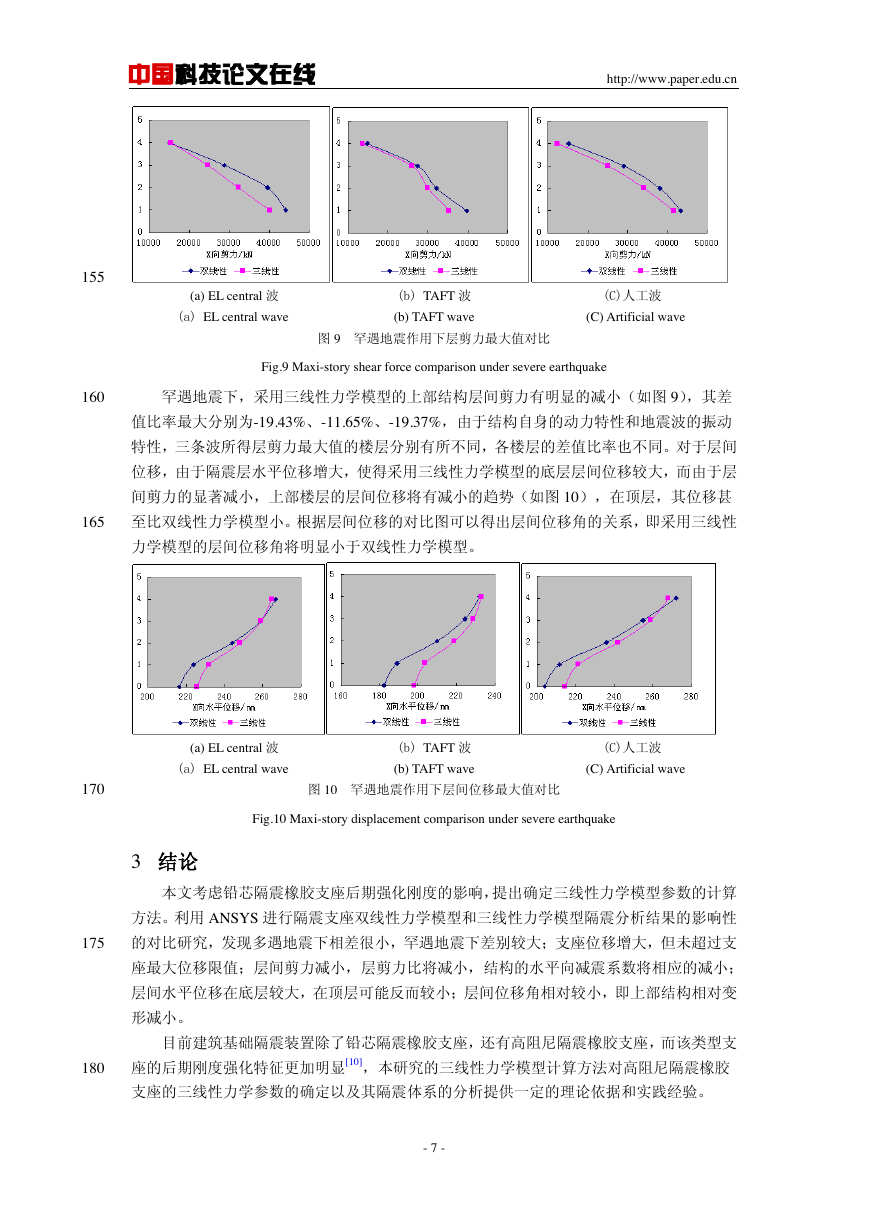
    中国科技论文在线 http://www.paper.edu.cn 155 (a) EL central 波 (b) TAFT 波 (C)人工波 (a) EL central wave (b) TAFT wave (C) Artificial wave 图 9 罕遇地震作用下层剪力最大值对比 Fig.9 Maxi-story shear force comparison under severe earthquake 160 罕遇地震下，采用三线性力学模型的上部结构层间剪力有明显的减小（如图 9），其差 值比率最大分别为-19.43%、-11.65%、-19.37%，由于结构自身的动力特性和地震波的振动 特性，三条波所得层剪力最大值的楼层分别有所不同，各楼层的差值比率也不同。对于层间 位移，由于隔震层水平位移增大，使得采用三线性力学模型的底层层间位移较大，而由于层 间剪力的显著减小，上部楼层的层间位移将有减小的趋势（如图 10），在顶层，其位移甚 165 至比双线性力学模型小。根据层间位移的对比图可以得出层间位移角的关系，即采用三线性 力学模型的层间位移角将明显小于双线性力学模型。 (a) EL central 波 (b) TAFT 波 (C)人工波 (a) EL central wave (b) TAFT wave (C) Artificial wave 170 图 10 罕遇地震作用下层间位移最大值对比 Fig.10 Maxi-story displacement comparison under severe earthquake 3 结论 本文考虑铅芯隔震橡胶支座后期强化刚度的影响，提出确定三线性力学模型参数的计算 方法。利用 ANSYS 进行隔震支座双线性力学模型和三线性力学模型隔震分析结果的影响性 175 的对比研究，发现多遇地震下相差很小，罕遇地震下差别较大；支座位移增大，但未超过支 座最大位移限值；层间剪力减小，层剪力比将减小，结构的水平向减震系数将相应的减小； 层间水平位移在底层较大，在顶层可能反而较小；层间位移角相对较小，即上部结构相对变 形减小。 目前建筑基础隔震装置除了铅芯隔震橡胶支座，还有高阻尼隔震橡胶支座，而该类型支 180 座的后期刚度强化特征更加明显[10]，本研究的三线性力学模型计算方法对高阻尼隔震橡胶 支座的三线性力学参数的确定以及其隔震体系的分析提供一定的理论依据和实践经验。 - 7 -
    中国科技论文在线 http://www.paper.edu.cn [参考文献] (References) 185 190 195 [1] 唐家祥.建筑结构基础隔震[M]. 武汉:华中理工大学出版社,1993 [2] 党育，杜永峰，李慧.基础隔震结构设计及施工指南[M].北京:中国水利水电出版社，2007 [3] 周云.耗能减震加固技术与设计方法[M]. 北京:科学出版社,2006 [4] 日本建筑学会.隔震结构设计[M]. 北京:地震出版社,2006 [5] 袁涌，朱宏平，资道铭. 高阻尼橡胶隔震支座的力学性能及隔震效果分析研究[J]，预应力技术，2011， 84(1)：20-23 [6] A.B.M.Saiful Islam,Raja Rizwan Hussain.Non-linear time domain analysis of base isolated muti-storey building under site specific bi-directional seismic loading[J].Automation in Construction,2012,22(3):554-566. [7] Philippe Gueguen.Experimental analysis of seismic response of one base-isolation building according to different levels of shaking:example of the Martinique earthquake[J].Bull Earthquake Eng,2012,10(4):1285-1298 [8] 北京金土木软件技术有限公司.Pushover 分析在建筑工程抗震设计中的应用[M].中国建筑工业出版社， 2010.11~12 [9] 住房和城乡建设部，GB50011-2010.建筑抗震设计规范及条文说明[S].北京：中国建筑出版社，2010 [10] 朱坤.高阻尼橡胶支座力学性能及其隔震效果分析研究[D]. 武汉：华中科技大学,2009 - 8 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料