logo资料库

时间序列分析 ARIMA.ppt

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：1.73M 资料格式：ppt 举报 版权申诉
第1页 / 共33页
第2页 / 共33页
第3页 / 共33页
第4页 / 共33页
第5页 / 共33页
第6页 / 共33页
第7页 / 共33页
第8页 / 共33页
资料共33页，剩余部分请下载后查看
    确定性时间序列模型及 SARIMA模型的应用
    引言 所谓时间序列就是按照时间的顺序把随机 事件变化发展的过程记录下来的一列有序数据。 对时间序列进行观察、研究，找寻它变化发展 的规律，预测它将来的走势就是时间序列分析。 时间序列预测方法是通过时间序列的历史数据 揭示现象随时间变化的规律,将这种规律延伸 到未来，从而对该现象的未来做出预测。时间 序列预测方法分为两大类:一类是确定性时间 序列分析方法,另一类是随机性时间序列分析 方法。本文应用时间序列分析法对某地区社会 消费品零售总额进行分析研究。
    引言 社会消费品零售总额是指各种经济类型的 批发零售贸易业、餐饮业、制造业和其他行业 对城乡居民和社会集团的消费品零售额和农民 对非农业居民零售额的总和。它能够反映各行 业通过多种商品流通渠道向居民和社会集团供 应的生活消费品总量,是研究国内零售市场变动 情况、反映经济景气程度的重要指标,也是政府 进行宏观经济调控的重要依据。鉴于此,对我国 社会消费品零售额进行事前的预测分析就显得 十分必要,将有助于对我国经济走向进行分析并 进行相关决策，了解未来经济发展态势。
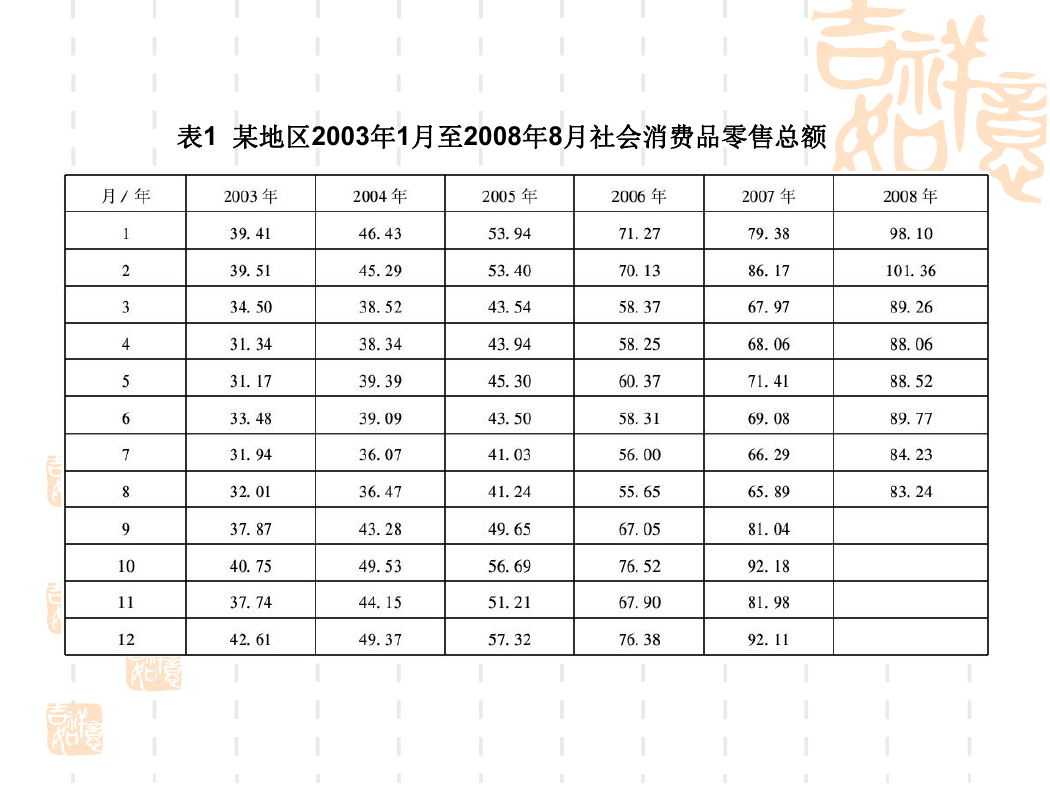
    引言 本文选取2003年1月至2008年8月各月某 地区社会消费品零售总额资料(见表1),借助 于EXCEL及EVIEWS软件对数据进行处理,运用 时间序列的确定性因素分解方法和SARIMA(季 节 间 列 型 析 0 8 至 0 9 年12月社会消费品零售总额进行预测。为检 验模型的效果,将2008年1月至8月的观测值作 为评价预测精度的参照对象。
    表1 某地区2003年1月至2008年8月社会消费品零售总额
    1. 确定性时间序列模型分析 T T 确定性时间序列分析的特点是认为数据 去掉随机扰动后,剩下的部分可以用确定的 时间函数来表示。最常用的确定性时间序列 分析方法是确定性因素分解方法,它把时间 序列分解成四个部分:趋势项(T)、季节项 (S)、循环项(C)和随机项(I)，通常把T和C 并在一起统称为趋势波动。常见的确定性时 间序列模型有:加法模型( ),乘 法 模 型 ( ） 及 混 合 模 型 S ( ）。 T T    x t S I t I   t t t t t x t  S t  ( T t x t   I t )
    确定性时间序列分析的流程图： 绘制 时序图 选择 拟合模型 计算 季节指数 消除季节影响 拟合趋势变动规律 残差检验 短期预测 本文采用混合模型进行分析预测，基本 思想是先分离出时间序列的基本趋势 和 季 节 波 动 （ 本 文 数 据 为 月 度 数 据 ， 故 ），然后按混合模型进行组合而 得到预测模型： 1,2, jF ( ) t  ,12 j  f x t  ( ) f t F  j
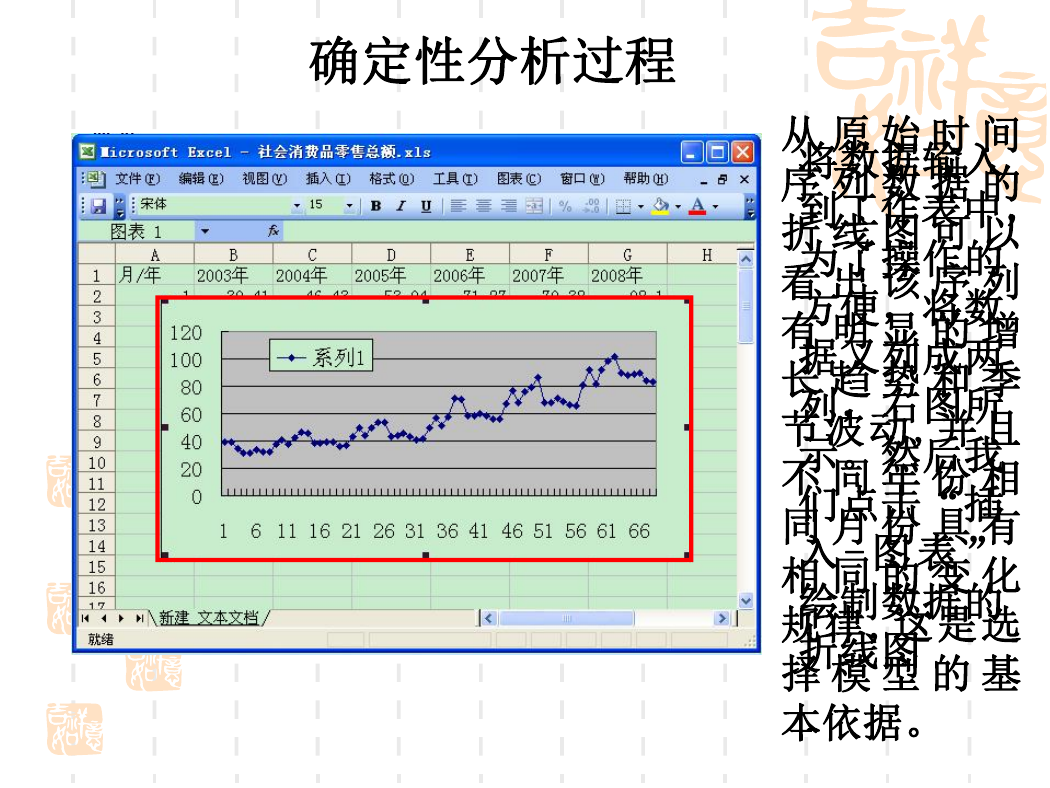
    确定性分析过程 从 原 始 时 间 将数据输入 序 列 数 据 的 到工作表中， 折 线 图 可 以 为了操作的 看 出 该 序 列 方便，将数 有 明 显 的 增 据又列成两 长 趋 势 和 季 列，右图所 节波动,并且 示。然后我 不 同 年 份 相 们点击“插 同 月 份 具 有 入 - 图 表 ” 相 同 的 变 化 绘制数据的 规律,这是选 折线图 择 模 型 的 基 本依据。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料