第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
信号与系统实验报告.doc
武汉大学教学实验报告
电子信息学院 通信工程 专业
2014 年 10 月 31 日
实验名称
周期信号的合成与分解
指导教师
姓名 虞延平 年级 2012 学号 2012301200010 成绩
一、 预习部分
1. 实验目的
2. 实验基本原理
3. 主要仪器设备（含必要的元器件、工具）
一.实验目的：
1．在理论学习的基础上，通过实验深刻领会周期信号傅里叶级数分解的物理意
义；
2．理解实际应用中通常采用有限项级数来逼近无限项级数，此时方均误差随项
数的增加而减小；
3．观察并初步了解 Gibbs 现象；
4．深入理解周期信号的频谱特点，比较不同周期信号频谱的差异。
二．实验原理：
满足Dirichlet 条件的周期信号f(t)可以分解成三角函数形式的傅里叶级
表达式为:
f
( )
t
a
0
a
1
cos(
t
1
)
b
1
sin(
t
1
)
a
cos(
n t
1
)
b
sin(
n t
1
)
n
n
a
0
n
1
[
a
n
cos(
n t
1
)
b
n
sin(
n t
1
)]
式中n为正整数；角频率 1 由周期T1 决定。该式表明：任何满足Dirichlet 条
件的周期信号都可以分解成直流分量及许多正弦、余弦分量。这些正弦、余弦分
量的频率必定是基频f1 的整数倍。通常把频率为f1 的分量称为基波，频率为nf1 的
分量称为n 次谐波。周期信号的频谱只会出现在0,
1, 2 1,…,n 1,… 等离散的频
率点上，这种频谱称为离散谱，是周期信号频谱的主要特点。 ( )
t 波形变化越
f
剧烈，所包含的高频分量的比重就越大；变化越平缓，所包含的低频分量的比重
就越大。
一般来说，将周期信号分解得到的三角函数形式的傅里叶级数的项数是无限的。
也就是说，通常只有无穷项的傅里叶级数才能与原函数精确相等。但在实际应用
中，显然无法取至无穷多项，而只能采用有限项级数来逼近无穷项级数。而且，
所取项数越多，有限项级数就越逼近原函数，原函数与有限项级数间的方均误差
就越小，而且低次谐波分量的系数不会因为所取项数的增加而变化。当选取的傅
里叶有限级数的项数越多，所合成的波形的峰起就越靠近 f(t)的不连续点。当
所取得项数 N 很大时，该峰起值趋于一个常数，约等于总跳变值的 9%，这种现
象称为 Gibbs 现象。
三．主要仪器设备：
1.实验环境：matlab 软件环境
2.主要用到的 matlab 函数：
① subplot: divides the current figure into rectangular panes that are
numbered rowwise.
② plot: 2-D line plot.
③ max: Largest elements in array.
④ stem：Plot discrete sequence data.
二、 实验操作部分
1. 实验数据、表格及数据处理
2. 实验操作过程（可用图表示）
3. 实验结论
1.实验内容：
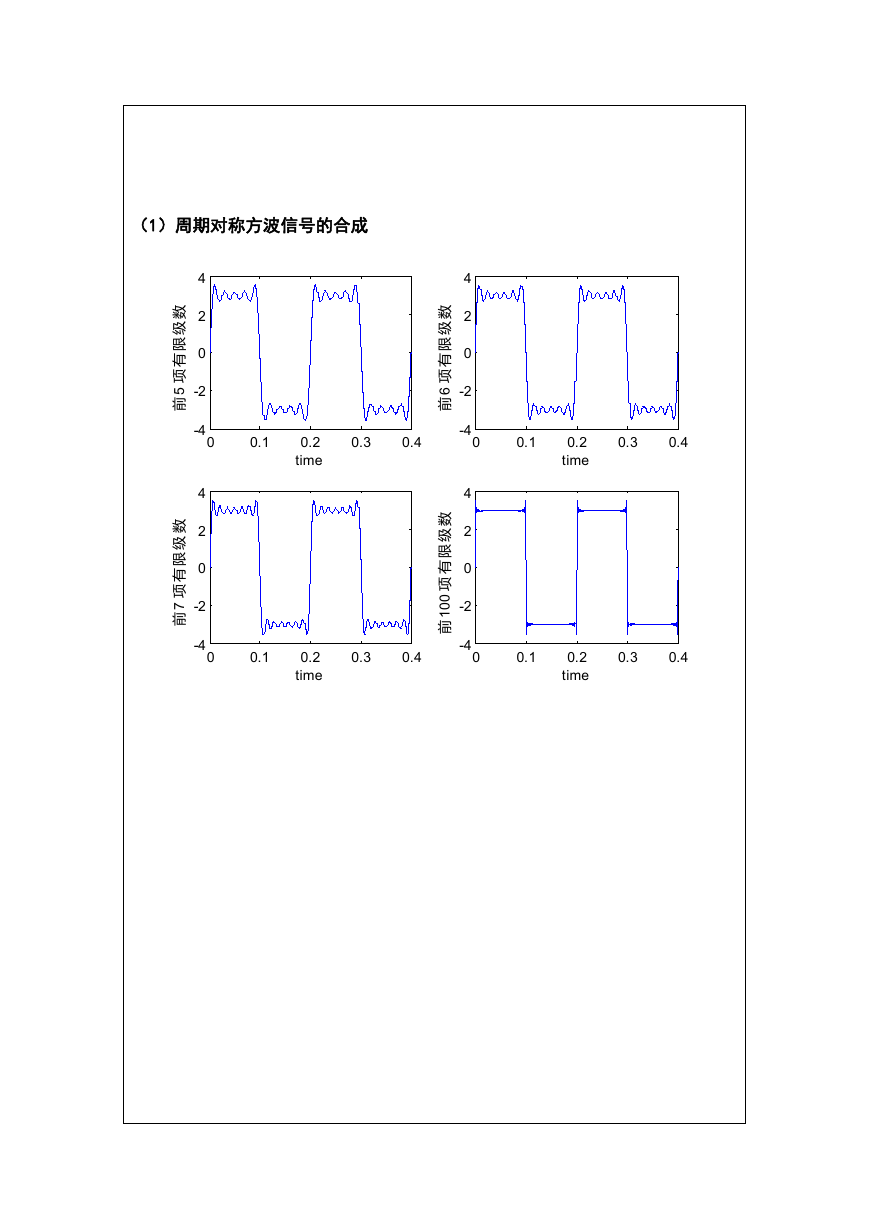
（1）周期对称方波信号的合成
周期奇对称方波信号可以用无穷个奇次谐波分量的傅里叶级数来表示：
f
( )
t
2
E
1
n
2
n
0
sin[(2
n
1)
t
1
]
1
选取奇对称周期方波的周期 T=0.02s，幅度 E=6，采用有限项级数来逼近该函数。
分别取前 1、2、5 和 100 项有限级数来近似，在 M 文件中编写程序并把结果显示在
一幅图中，观察它们逼近方波的过程。
（2）观察 Gibbs 现象并计算峰起值 w
在 M 文件中编写程序，分别取前 5,6,7 和 100 项有限级数来逼近奇对称方波，观
察 Gibbs 现象，并且分别计算峰起值 Gibbs，并且在图像中显示出来。观察峰起
值 gibbs 与 0.09 关系。
（3）周期奇对称三角信号的合成，观察 Gibbs 现象并计算峰起值
周期奇对称方三角波号可以用无穷个奇次谐波分量的傅里叶级数来表示：
f
( )
t
1
2
E
2n
n
0
sin[2
n t
1
]
设计采用有限项级数逼近奇对称周期三角信号的实验， 分别取前1、5、25 和
100项有限级数来逼近奇对称三角信号，在M文件中编写程序，观察 Gibbs 现象，
并且分别计算峰起值 z，并且在图像中显示出来。观察峰起值 zx 与 0.09 关系。
4． 周期信号的频谱
分析奇对称方波信号与偶对称三角信号的频谱，编制程序并显示结果，深入
讨论周期信号的频谱特点和两信号频谱的差异。
2.实验过程：
（1）周期对称方波信号的合成
%奇对称方波合成
%奇对称方波合成
clear
clc
Fs=10000;
T = 1/Fs;
t=0:0.0001:100;
y=0;
for i=1:100
y=y+pi/12*(sin((2*i-1)*20*pi*t)/(2*i-1));
end
figure(1)
plot(t,y);
axis([0,1,-0.5,0.5]);
xlabel('time');
ylabel('前 100 项有限级数');
N=length(t)-1;
NFFT = 2^nextpow2(N); % Next power of 2 from length of y
Y = fft(y,NFFT)/N;
f = Fs/2*linspace(0,1,NFFT/2+1);
figure(2)
plot(f,2*abs(Y(1:NFFT/2+1)))
axis([0,100,0,0.5]);
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
（2）观察 Gibbs 现象并计算峰起值 Gibbs
%奇对称方波合成
%观察 Gibbs 现象
Gibbs=0;
gibbs=0;
t=0:0.0001:0.4;
sishu=12/pi;
y=0;
for i=1:5
y=y+sishu*(sin((2*i-1)*10*pi*t)/(2*i-1));
end
subplot(221)
plot(t,y);
axis([0,0.4,-4,4]);
Gibbs=max(y);
gibbs=num2str((Gibbs-3)/6);
text(0.03,2,gibbs);
xlabel('time');
ylabel('前5 项有限级数');
Gibbs=0;
gibbs=0;
y=0;
for i=1:6
y=y+sishu*(sin((2*i-1)*10*pi*t)/(2*i-1));
end
subplot(222);
plot(t,y);
axis([0,0.4,-4,4]);
Gibbs=max(y);
gibbs=num2str((Gibbs-3)/6);
text(0.03,2,gibbs);
xlabel('time');
ylabel('前6 项有限级数');
Gibbs=0;
gibbs=0;
y=0;
for i=1:7
y=y+sishu*(sin((2*i-1)*10*pi*t)/(2*i-1));
end
subplot(223)
plot(t,y);
axis([0,0.4,-4,4]);
Gibbs=max(y);
gibbs=num2str((Gibbs-3)/6);
text(0.03,2,gibbs);
xlabel('time');
ylabel('前7 项有限级数');
Gibbs=0;
gibbs=0;
y=0;
for i=1:100
y=y+sishu*(sin((2*i-1)*10*pi*t)/(2*i-1));
end
subplot(224)
plot(t,y);
axis([0,0.4,-4,4]);
Gibbs=max(y);
gibbs=num2str((Gibbs-3)/6);
text(0.03,2,gibbs);
xlabel('time');
ylabel('前100 项有限级数');
（3）周期奇对称三角信号的合成，观察 Gibbs 现象并计算峰起值
%奇对称三角波合成
clear
clc
Fs=10000;
T = 1/Fs;
t=0:0.0001:100;
y=0;
for i=1:100
y=y+(1/pi*(-1)^(i+1))/i*sin(i*20*pi*t);
end
figure(1)
plot(t,y);
axis([0,1,-1,1]);
xlabel('time');
ylabel('前 100 项有限级数');
N=length(t)-1;
NFFT = 2^nextpow2(N); % Next power of 2 from length of y
Y = fft(y,NFFT)/N;
f = Fs/2*linspace(0,1,NFFT/2+1);
figure(2)
MagY=2*abs(Y(1:NFFT/2+1));
plot(f,2*abs(Y(1:NFFT/2+1)))
axis([0,50,0,0.5]);
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
（1）周期对称方波信号的合成
数
级
限
有
项
5
前
数
级
限
有
项
7
前
4
2
0
-2
-4
0
4
2
0
-2
-4
0
数
级
限
有
项
6
前
数
级
限
有
项
0
0
1
前
4
2
0
-2
-4
0
4
2
0
-2
-4
0
0.1
0.2
time
0.3
0.4
0.1
0.2
time
0.3
0.4
0.1
0.2
time
0.3
0.4
0.1
0.2
time
0.3
0.4
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
