logo资料库

eviews面板数据模型详解.doc

发布时间：2022-06-16 发布人：admin 分类：说明书 资料大小：0.84M 资料格式：doc 举报 版权申诉
第1页 / 共22页
第2页 / 共22页
第3页 / 共22页
第4页 / 共22页
第5页 / 共22页
第6页 / 共22页
第7页 / 共22页
第8页 / 共22页
资料共22页，剩余部分请下载后查看
    1.已知 1996—2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均消费 （ cp ，不变价格）和人均收入（ip ，不变价格）居民，利用数据（1）建立面板 数据（panel data）工作文件；（2）定义序列名并输入数据；（3）估计选择面板 模型；（4）面板单位根检验。 年人均消费（consume）和人均收入（income）数据以及消费者价格指数（p）分别见表 9.1，9.2 和 9.3。 表 9.1 1996—2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均消费（元）数据 人均消费 1996 1997 1998 1999 2000 2001 2002 CONSUMEAH 3607.43 3693.55 3777.41 3901.81 4232.98 4517.65 4736.52 CONSUMEBJ 5729.52 6531.81 6970.83 7498.48 8493.49 8922.72 10284.6 CONSUMEFJ 4248.47 4935.95 5181.45 5266.69 5638.74 6015.11 6631.68 CONSUMEHB 3424.35 4003.71 3834.43 4026.3 4348.47 4479.75 5069.28 CONSUMEHLJ 3110.92 3213.42 3303.15 3481.74 3824.44 4192.36 4462.08 CONSUMEJL 3037.32 3408.03 3449.74 3661.68 4020.87 4337.22 4973.88 CONSUMEJS 4057.5 4533.57 4889.43 5010.91 5323.18 5532.74 6042.6 CONSUMEJX 2942.11 3199.61 3266.81 3482.33 3623.56 3894.51 4549.32 CONSUMELN 3493.02 3719.91 3890.74 3989.93 4356.06 4654.42 5342.64 CONSUMENMG 2767.84 3032.3 3105.74 3468.99 3927.75 4195.62 4859.88 CONSUMESD 3770.99 4040.63 4143.96 4515.05 5022 5252.41 5596.32 CONSUMESH 6763.12 6819.94 6866.41 8247.69 8868.19 9336.1 10464 CONSUMESX 3035.59 3228.71 3267.7 3492.98 3941.87 4123.01 4710.96 CONSUMETJ 4679.61 5204.15 5471.01 5851.53 6121.04 6987.22 7191.96 CONSUMEZJ 5764.27 6170.14 6217.93 6521.54 7020.22 7952.39 8713.08 表 9.2 1996—2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均收入（元）数据 人均收入 1996 1997 1998 1999 2000 2001 2002 INCOMEAH 4512.77 4599.27 4770.47 5064.6 5293.55 5668.8 6032.4 INCOMEBJ 7332.01 7813.16 8471.98 9182.76 10349.69 11577.78 12463.92 INCOMEFJ 5172.93 6143.64 6485.63 6859.81 7432.26 8313.08 9189.36 INCOMEHB 4442.81 4958.67 5084.64 5365.03 5661.16 5984.82 6679.68 INCOMEHLJ 3768.31 4090.72 4268.5 4595.14 4912.88 5425.87 6100.56 INCOMEJL 3805.53 4190.58 4206.64 4480.01 4810 5340.46 6260.16 INCOMEJS 5185.79 5765.2 6017.85 6538.2 6800.23 7375.1 8177.64 INCOMEJX 3780.2 4071.32 4251.42 4720.58 5103.58 5506.02 6335.64 INCOMELN 4207.23 4518.1 4617.24 4898.61 5357.79 5797.01 6524.52 INCOMENMG 3431.81 3944.67 4353.02 4770.53 5129.05 5535.89 6051 INCOMESD 4890.28 5190.79 5380.08 5808.96 6489.97 7101.08 7614.36 INCOMESH 8178.48 8438.89 8773.1 10931.64 11718.01 12883.46 13249.8 INCOMESX 3702.69 3989.92 4098.73 4342.61 4724.11 5391.05 6234.36 INCOMETJ 5967.71 6608.39 7110.54 7649.83 8140.5 8958.7 9337.56 INCOMEZJ 6955.79 7358.72 7836.76 8427.95 9279.16 10464.67 11715.6
    表 9.3 1996—2002 年中国东北、华北、华东 15 个省级地区的消费者物价指数 物价指数 1996 1997 1998 1999 2000 2001 PAH PBJ PFJ PHB 109.9 101.3 100 97.8 100.7 100.5 111.6 105.3 102.4 100.6 103.5 103.1 105.9 101.7 99.7 99.1 102.1 98.7 107.1 103.5 98.4 98.1 99.7 100.5 PHLJ 107.1 104.4 100.4 96.8 98.3 100.8 PJL PJS PJX PLN 107.2 103.7 99.2 98 98.6 101.3 109.3 101.7 99.4 98.7 100.1 100.8 108.4 102 101 98.6 100.3 99.5 107.9 103.1 99.3 98.6 99.9 100 PNMG 107.6 104.5 99.3 99.8 101.3 100.6 PSD PSH PSX PTJ PZJ 109.6 102.8 99.4 99.3 100.2 101.8 109.2 102.8 100 101.5 102.5 100 107.9 103.1 98.6 99.6 103.9 99.8 109 103.1 99.5 107.9 102.8 99.7 98.9 98.8 99.6 101.2 101 99.8 2002 99 98.2 99.5 99 99.3 99.5 99.2 100.1 98.9 100.2 99.3 100.5 98.4 99.6 99.1 （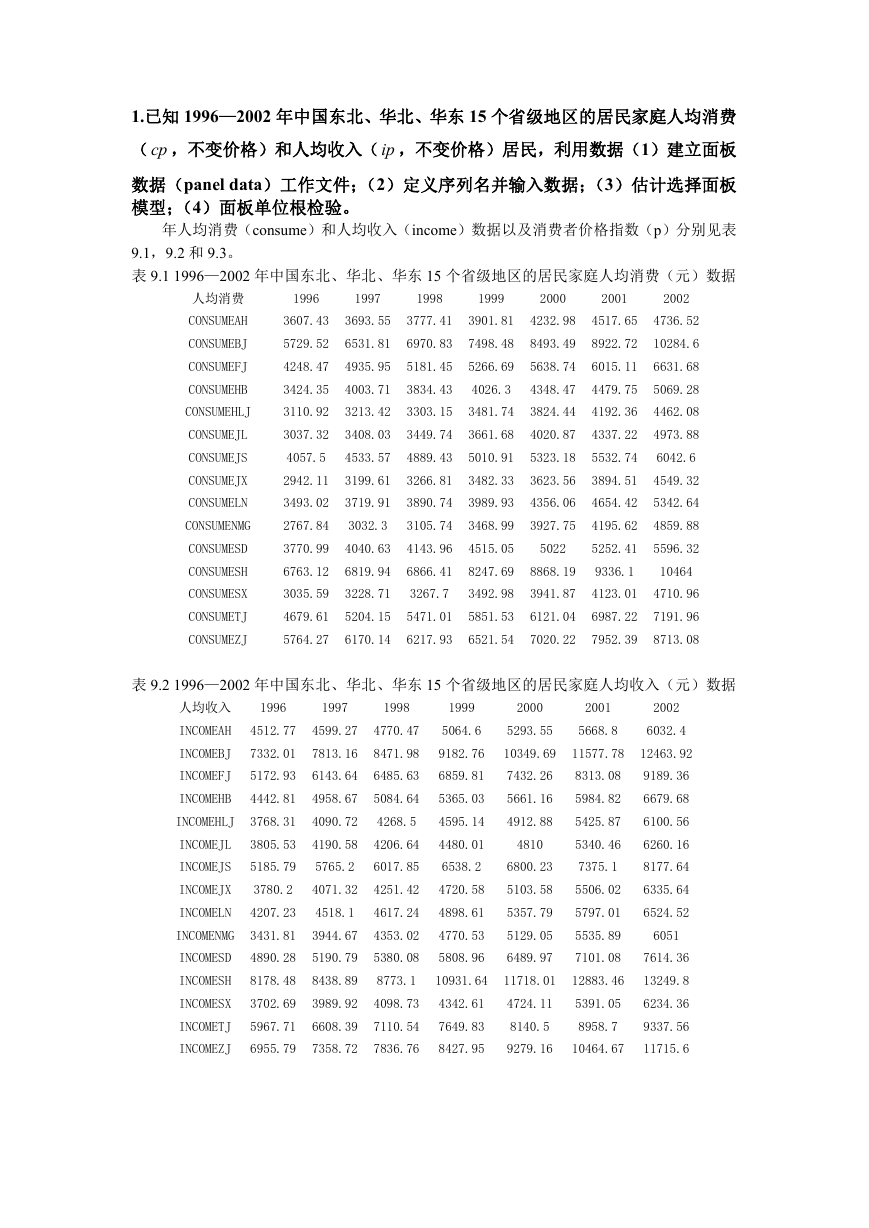1）建立面板数据工作文件 首先建立工作文件。打开工作文件后，过程如下：
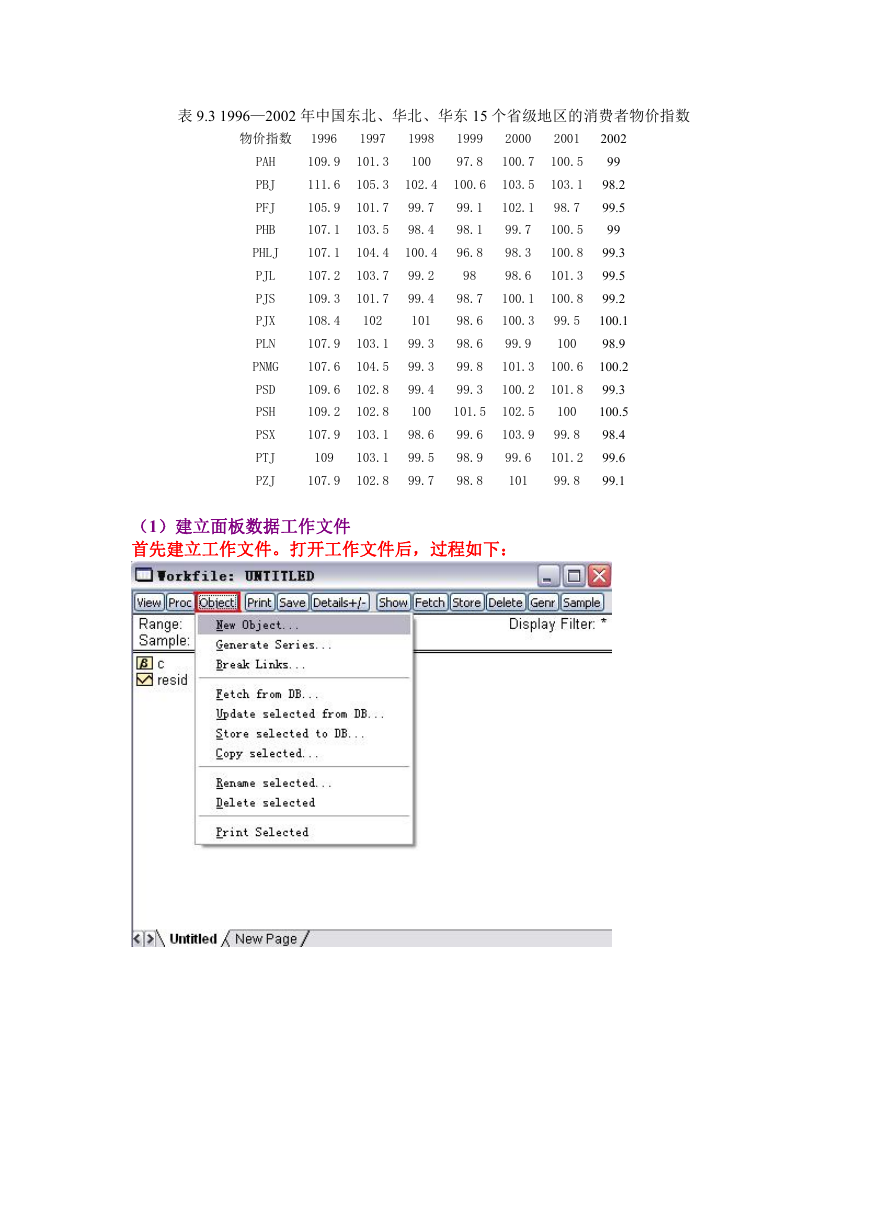
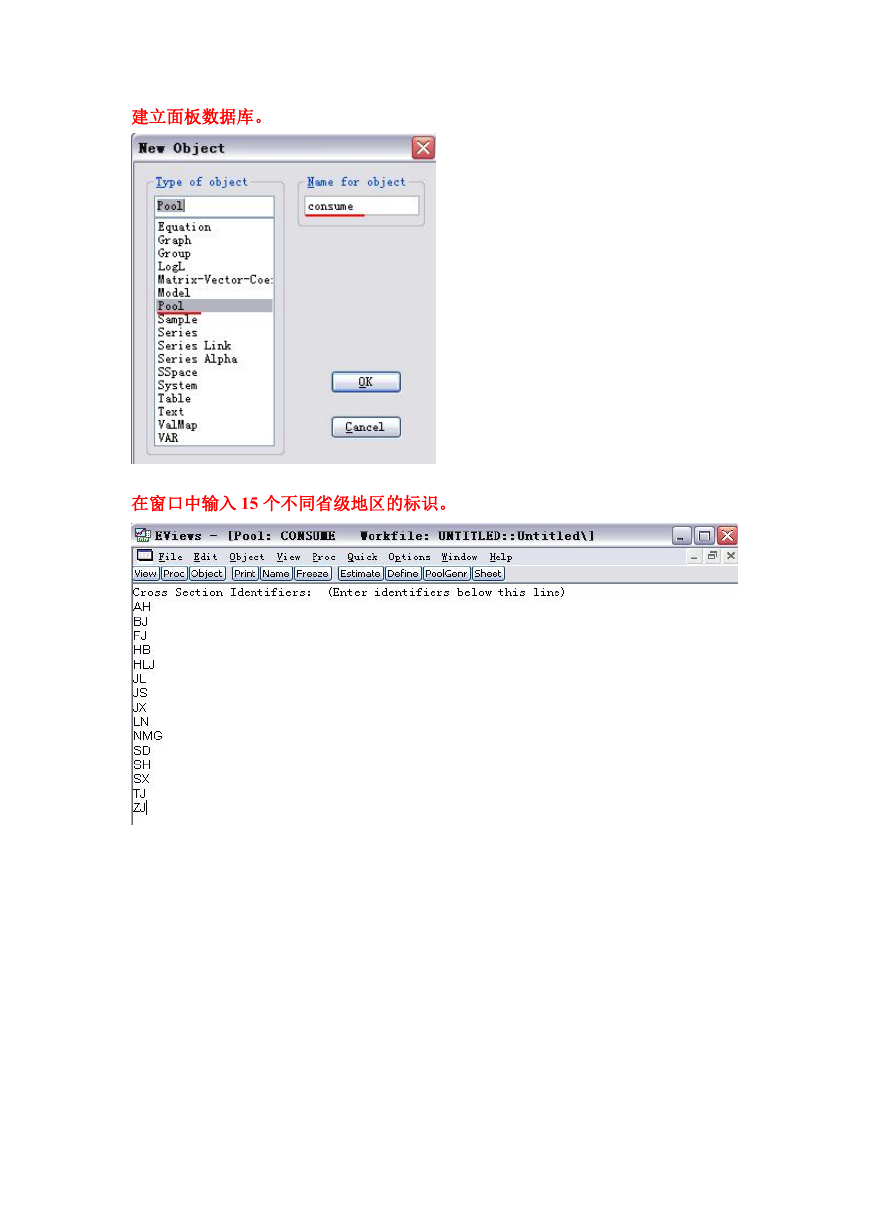
    建立面板数据库。 在窗口中输入 15 个不同省级地区的标识。
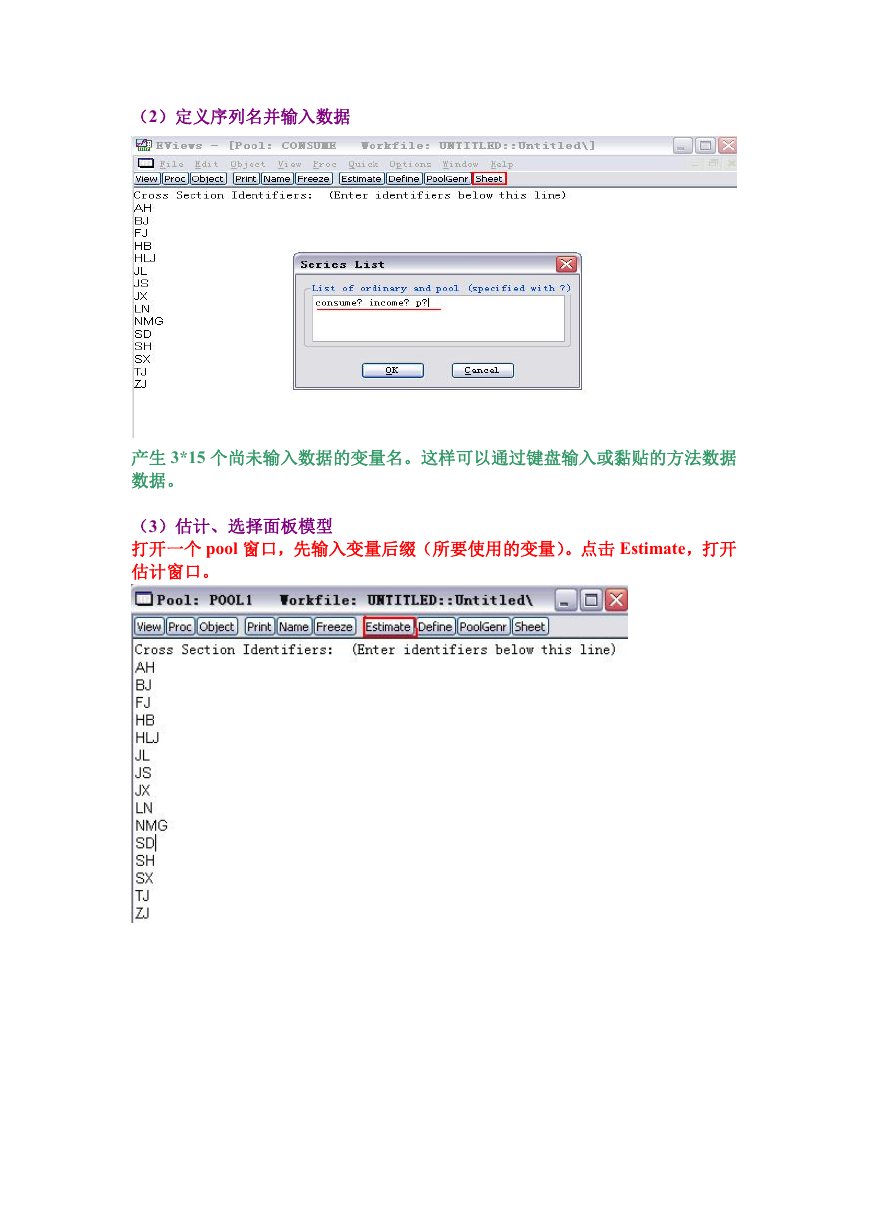
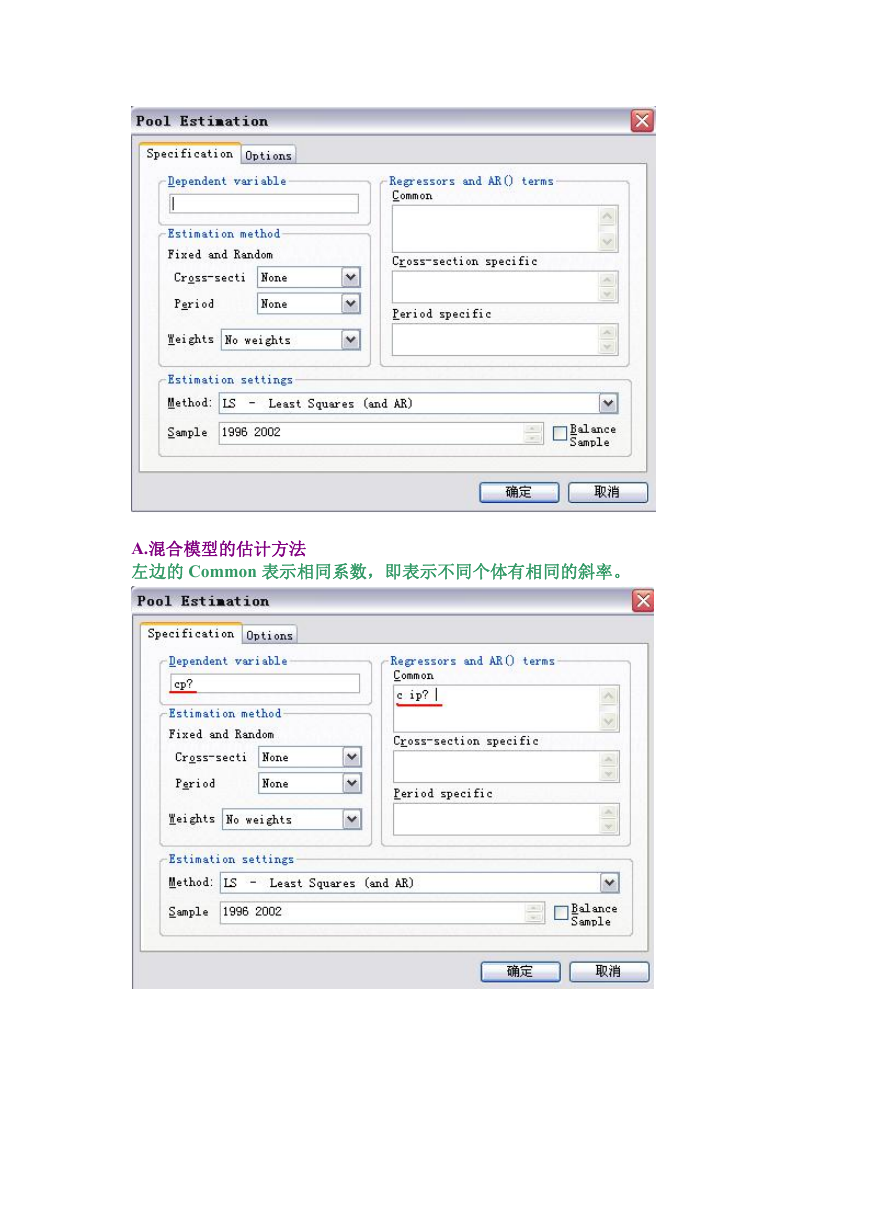
    （2）定义序列名并输入数据 产生 3*15 个尚未输入数据的变量名。这样可以通过键盘输入或黏贴的方法数据 数据。 （3）估计、选择面板模型 打开一个 pool 窗口，先输入变量后缀（所要使用的变量）。点击 Estimate，打开 估计窗口。
    A.混合模型的估计方法 左边的 Common 表示相同系数，即表示不同个体有相同的斜率。
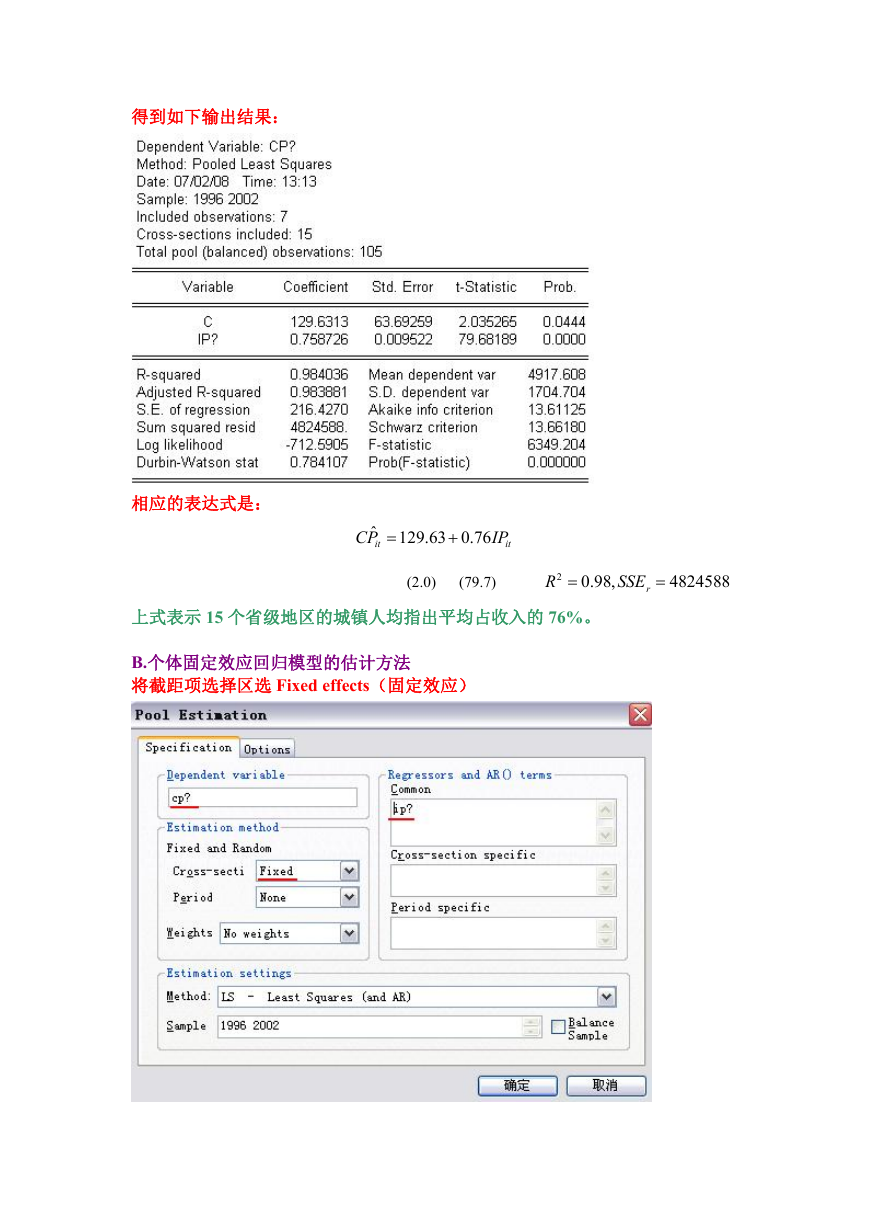
    得到如下输出结果： 相应的表达式是： ˆ CP it  129.63 0.76  IP it 上式表示 15 个省级地区的城镇人均指出平均占收入的 76%。 (2.0) (79.7) 2 R  0.98, SSE r  4824588 B.个体固定效应回归模型的估计方法 将截距项选择区选 Fixed effects（固定效应）
    得到如下输出结果： 相应的表达式为： ˆ CP it  515.6 0.70  IP it  36.3 D 1  537.6 D 2   ... 198.6 D 15 (6.3) (55) 2 R  0.99, SSE r  2270386 其中虚拟变量 1 D D 2 , ,..., D 的定义是： 15 D i     1, 0, i 如果属于第 个个体, 1,2,...,15 其他  i 15 个省级地区的城镇人均指出平均占收入 70%。从上面的结果可以看出北京市
    居民的自发性消费明显高于其他地区。 接下来用 F 统计量检验是应该建立混合回归模型，还是个体固定效应回归模型。 0H ： i  。模型中不同个体的截距相同（真实模型为混合回归模型）。 1H ：模型中不同个体的截距项 i不同（真实模型为个体固定效应回归模型）。 F 统计量定义为：   ( SSE )] F  r ) /[( SSE u SSE u 1) NT k / (  (    NT N k  NT N k  )  ( SSE r SSE u 1) N SSE   u / ( ) NT N k  ) / (  其中 SSE 表示约束模型，即混合估计模型的残差平方和， r SSE 表示非约束模型，即 u 1N  个被估参数。 个体固定效应回归模型的残差平方和。非约束模型比约束模型多了 所以本例中： F   (4824588 227386) / (15 1)  2270386 / (105 15 1)    8.1  F 0.05 (14,89) 1.8  所以推翻原假设，建立个体固定效应回归模型更合理。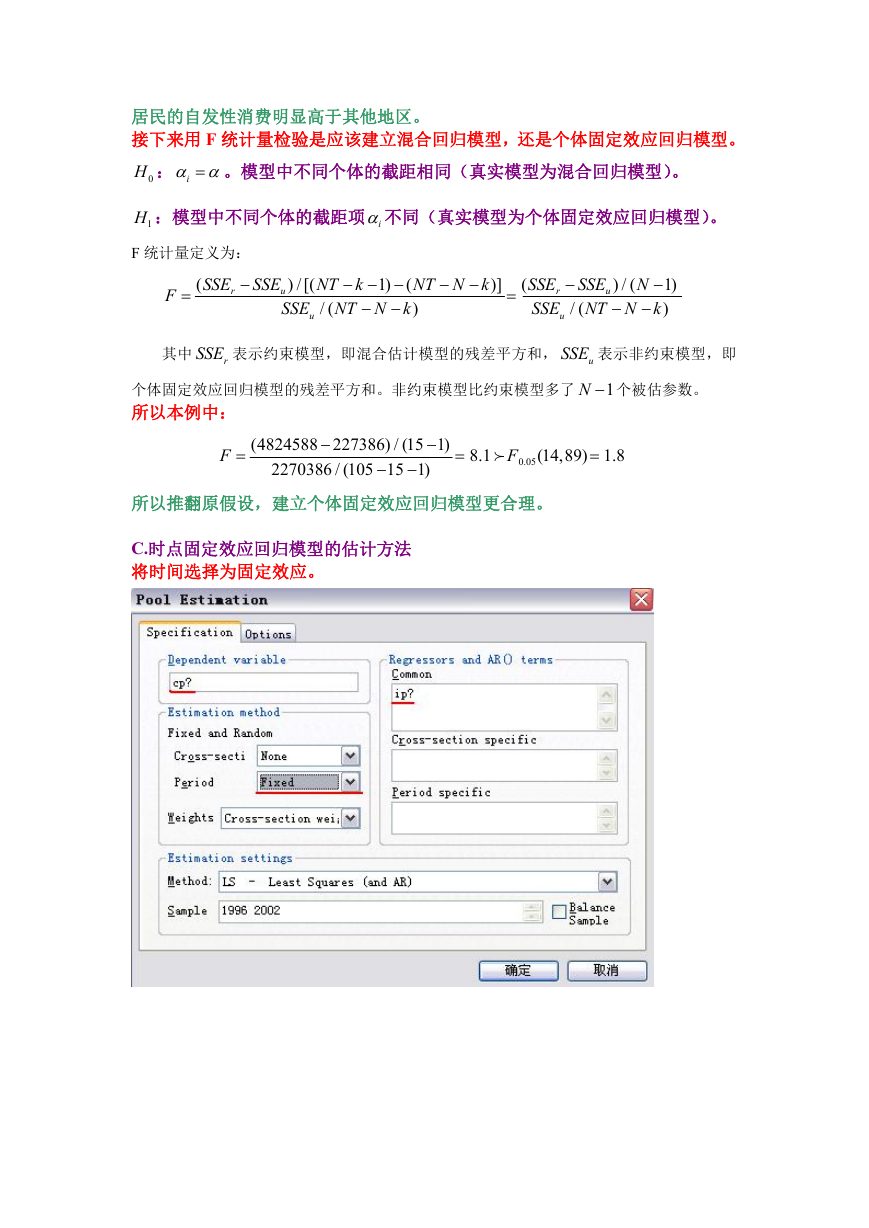 C.时点固定效应回归模型的估计方法 将时间选择为固定效应。
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料