第1页 / 共34页
第2页 / 共34页
第3页 / 共34页
第4页 / 共34页
第5页 / 共34页
第6页 / 共34页
第7页 / 共34页
第8页 / 共34页
图卷积网络Graph Convolutional Network（GCN）的理解和详细推导.pdf
1. 为什么会出现图卷积神经网络？
2. 图卷积网络的两种理解方式
2.1 vertex domain(spatial domain)：顶点域（空间域）
2.2 spectral domain：频域方法（谱方法）
3. 什么是拉普拉斯矩阵？
3.1 常用的几种拉普拉斯矩阵
普通形式的拉普拉斯矩阵
对称归一化的拉普拉斯矩阵（Symmetric normalized Laplacian）
随机游走归一化拉普拉斯矩阵（Random walk normalized Laplacian）
泛化的拉普拉斯 (Generalized Laplacian)
3.2 无向图的拉普拉斯矩阵有什么性质
3.3 为什么GCN要用拉普拉斯矩阵？
3.4. 拉普拉斯矩阵的谱分解（特征分解）
3.5 拉普拉斯算子
4. 如何通俗易懂地理解卷积？
4.1 连续形式的一维卷积
4.2 离散形式的一维卷积
4.3 实例:掷骰子问题
5. 傅里叶变换
5.1 连续形式的傅立叶变换
5.2 频域（frequency domain）和时域（time domain）的理解
5.3 周期性离散傅里叶变换（Discrete Fourier Transform, DFT）
6. Graph上的傅里叶变换及卷积
6.1 图上的傅里叶变换
6.2 图的傅立叶变换——图的傅立叶变换的矩阵形式
6.3 图的傅立叶逆变换——图的傅立叶逆变换的矩阵形式
6.4 图上的傅里叶变换推广到图卷积
7. 为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？特征值表示频率？
7.1 为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？
7.2 怎么理解拉普拉斯矩阵的特征值表示频率？
8. 深度学习中GCN的演变
8.1 Spectral CNN
8.2 Chebyshev谱CNN（ChebNet）
8.3 CayleyNet
8.4 一阶ChebNet（1stChebNet）-GCN
GCN的优点
GCN的不足
9. GCN的一些改进
9.1 邻接矩阵的探索
Adaptive Graph Convolution Network (AGCN)
Dual Graph Convolutional Network(DGCN)
9.2 空间域的GCNs（ConvGNNs）
Neural Network for Graphs (NN4G)
Contextual Graph Markov Model (CGMM)
Diffusion Convolutional Neural Network (DCNN)扩散卷积神经网络
Diffusion Graph Convolution(DGC) 扩散图卷积
PGC-DGCNN
Partition Graph Convolution (PGC)
Message Passing Neural Networks (MPNN) 信息传递神经网络
Graph Isomorphism Network (GIN) 图同构网络
GraphSage
Graph Attention Network (GAT)图注意力网络
Gated Attention Network (GAAN)-门控注意力网络
Mixture Model Network (MoNet)
PATCHY-SAN
Large-scale Graph Convolution Networks (LGCN)
GraphSAGE
FastGCN
AS-GCN
StoGCN（或VR-GCN）
Cluster-GCN
复杂度对比
10. GCN的一些应用
11. GCN代码分析和数据集Cora、Pubmed、Citeseer格式
12. 从空间角度理解GCN
13. GCN处理不同类型的图
关于带权图问题
关于有向图问题
节点没有特征的图
14. 问题讨论
Q1：GCN中邻接矩阵为什么要归一化？
Q2:GCN中邻接矩阵为什么要renormalization？
Q3:GCN中参数矩阵W的维度如何确定？怎么理解GCN是transductive的？
Q4：为什么GCN里使用NELL数据集相比于其他三个的分类准确率这么低？
Q5：目前GCN的分类准确率仅为80%左右，如何提高GCN在Citeseer、Cora、Pubmed、Nell上的分类准确率？
Q6：增加GCN层数，为何准确率还降低了？
资料下载
参考
1. 为什么会出现图卷积神经网络？
普通卷积神经网络研究的对象是具备Euclidean domains的数据，Euclidean domains data数据最显著的特征是他们具有规则的空间结
构，如图片是规则的正方形，语音是规则的一维序列等，这些特征都可以用一维或二维的矩阵来表示，卷积神经网络处理起来比较高效。
CNN的【平移不变性】在【非矩阵结构】数据上不适用
平移不变性（translation invariance）：比较好理解，在用基础的分类结构比如ResNet、Inception给一只猫分类时，无论猫怎么扭
曲、平移，最终识别出来的都是猫，输入怎么变形输出都不变这就是平移不变性，网络的层次越深这个特性会越明显。
平移可变性（translation variance）：针对目标检测的，比如一只猫从图片左侧移到了右侧，检测出的猫的坐标会发生变化就称为
平移可变性。当卷积网络变深后最后一层卷积输出的feature map变小，物体在输入上的小偏移，经过N多层pooling后在最后的小
feature map上会感知不到，这就是为什么R-FCN原文会说网络变深平移可变性变差。
离散卷积本质就是一种加权求和。CNN中的卷积就是一种离散卷积，本质上就是利用一个共享参数的过滤器（kernel），通过计算中心像
素点以及相邻像素点的加权和来构成feature map实现空间特征的提取，当然加权系数就是卷积核的权重系数(W)。
那么卷积核的系数如何确定的呢？是随机化初值，然后根据误差函数通过反向传播梯度下降进行迭代优化。这是一个关键点，卷积核的参
数通过优化求出才能实现特征提取的作用，GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。
生活中很多数据不具备规则的空间结构，称为Non Euclidean data，如，推荐系统、电子交易、分子结构等抽象出来的图谱。这些图谱中
的每个节点连接不尽相同，有的节点有三个连接，有的节点只有一个连接，是不规则的结构。对于这些不规则的数据对象，普通卷积网络
的效果不尽人意。CNN卷积操作配合pooling等在结构规则的图像等数据上效果显著，但是如果作者考虑非欧氏空间比如图(即graph，流
形也是典型的非欧结构，这里作者只考虑图)，就难以选取固定的卷积核来适应整个图的不规则性，如邻居节点数量的不确定和节点顺序
的不确定。
例如，社交网络非常适合用图数据来表达，如社交网络中节点以及节点与节点之间的关系，用户A（有ID信息等）、用户B、帖子都是节
点，用户与用户之间的关系是关注，用户与帖子之间的关系可能是发布或者转发。通过这样一个图谱，可以分析用户对什么人、什么事感
兴趣，进一步实现推荐机制。
总结一下，图数据中的空间特征具有以下特点：
1） 节点特征：每个节点有自己的特征；（体现在点上）
2） 结构特征：图数据中的每个节点具有结构特征，即节点与节点存在一定的联系。（体现在边上）
总地来说，图数据既要考虑节点信息，也要考虑结构信息，图卷积神经网络就可以自动化地既学习节点特征，又能学习节点与节点之间的
关联信息。
综上所述，GCN是要为除CV、NLP之外的任务提供一种处理、研究的模型。
图卷积的核心思想是利用『边的信息』对『节点信息』进行『聚合』从而生成新的『节点表示』。
2. 图卷积网络的两种理解方式
GCN的本质目的就是用来提取拓扑图的空间特征。 而图卷积神经网络主要有两类，一类是基于空间域或顶点域vertex domain(spatial
domain)的，另一类则是基于频域或谱域spectral domain的。通俗点解释，空域可以类比到直接在图片的像素点上进行卷积，而频域可以
类比到对图片进行傅里叶变换后，再进行卷积。
所谓的两类其实就是从两个不同的角度理解，关于从空间角度的理解可以看本文的从空间角度理解GCN
2.1 vertex domain(spatial domain)：顶点域（空间域）
基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有
代表性的方法有 Message Passing Neural Networks(MPNN)[1], GraphSage[2], Diffusion Convolution Neural Networks(DCNN)[3],
PATCHY-SAN[4]等。
2.2 spectral domain：频域方法（谱方法）
这就是谱域图卷积网络的理论基础了。这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。从整个研究的时间进程来看：首先
研究GSP（graph signal processing）的学者定义了graph上的Fourier Transformation，进而定义了graph上的convolution，最后与深度
学习结合提出了Graph Convolutional Network。
基于频域卷积的方法则从图信号处理起家，包括 Spectral CNN[5], Cheybyshev Spectral CNN(ChebNet)[6], 和 First order of
ChebNet(1stChebNet)[7] 等
论文Semi-Supervised Classification with Graph Convolutional Networks就是一阶邻居的ChebNet
认真读到这里，脑海中应该会浮现出一系列问题：
Q1 什么是Spectral graph theory？
Spectral graph theory请参考维基百科的介绍，简单的概括就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质
Q2 GCN为什么要利用Spectral graph theory？
这是论文（Semi-Supervised Classification with Graph Convolutional Networks）中的重点和难点，要理解这个问题需要大量的数学定义
及推导
过程：
（1）定义graph上的Fourier Transformation傅里叶变换（利用Spectral graph theory，借助图的拉普拉斯矩阵的特征值和特征向量研究
图的性质）
（2）定义graph上的convolution卷积
下面将介绍关于频谱域的图卷积网络的推导相关的内容。
3. 什么是拉普拉斯矩阵？
拉普拉斯矩阵(Laplacian matrix) 也叫做导纳矩阵、基尔霍夫矩阵或离散拉普拉斯算子，主要应用在图论中，作为一个图的矩阵表示。对
于图 G=(V,E)，其Laplacian 矩阵的定义为 L=D-A，其中 L 是Laplacian 矩阵， D=diag(d)是顶点的度矩阵（对角矩阵）,d=rowSum(A)，
对角线上元素依次为各个顶点的度， A 是图的邻接矩阵。
Graph Fourier Transformation及Graph Convolution的定义都用到图的拉普拉斯矩阵。
频域卷积的前提条件是图必须是无向图，只考虑无向图，那么L就是对称矩阵。
3.1 常用的几种拉普拉斯矩阵
普通形式的拉普拉斯矩阵
L中的元素给定为：
L = D − A
L =i,j
⎪⎧diag(v )i
⎨
−1
⎩⎪
0
i = j
i = j and v is adjacent to v
otherwise
i
j
其中diag(vi) 表示顶点 i 的度。
对称归一化的拉普拉斯矩阵（Symmetric normalized Laplacian）
=sys D LD
L
−1/2
−1/2
=
I − D AD
−1/2
−1/2
矩阵元素定义为：
sys
=i,j
L
⎪⎪⎧1
⎨
−
⎩⎪⎪
0
1
i
diag(v )diag(v )
j
i = j and diag(v ) = 0
i = j and v is adjacent to v
otherwise
i
i
j
很多GCN的论文中应用的是这种拉普拉斯矩阵
随机游走归一化拉普拉斯矩阵（Random walk normalized Laplacian）
=rw D L =
L
−1
I − D A−1
矩阵元素定义为：
rw
=i,j
L
⎪⎧1
⎨
− diag(v )i
⎩⎪
0
1
泛化的拉普拉斯 (Generalized Laplacian)
泛化的拉普拉斯(用得少)定义为:
i,j
⎪⎧Q < 0
⎨
Q = 0
⎩⎪
anynumber
i,j
i
i = j and diag(v ) = 0
i = j and v is adjacent to v
otherwise
i
j
i = j and diag(v ) = 0
i = j and v is adjacent to v
otherwise
i
i
j
一个拉普拉斯矩阵的计算例子（依据于上图）：
1
1
0
1
0
0
⎪⎪⎪⎪⎪⎪⎧0
⎨
⎩⎪⎪⎪⎪⎪⎪
1
0
0
1
0
0
1
3
0
0
0
0
1
0
1
0
1
0
0
1
0
1
0
0
0
0
1
2
0
0
0
A =
⎪⎪⎪⎪⎪⎪⎪⎧
⎩⎪⎪⎪⎪⎪⎪⎪
⎨
1
2
0
0
0
0
0
0
0
1
0
1
1
0
0
0
1
3
0
0
−1/2
D
=
0
0
0
1
0
⎪⎪⎪⎪⎪⎪⎫
0⎭⎪⎪⎪⎪⎪⎪
⎬
，D =
⎪⎪⎪⎪⎪⎪⎧2
⎨
⎩⎪⎪⎪⎪⎪⎪
0
0
0
0
0
0
3
0
0
0
0
0
0
2
0
0
0
0
0
0
3
0
0
0
0
0
0
3
0
0
0
0
0
0
⎪⎪⎪⎪⎪⎪⎫
1⎭⎪⎪⎪⎪⎪⎪
⎬
, L =
D − A =
0
0
0
0
1
3
0
⎪⎪⎪⎪⎪⎪⎪⎫
⎭⎪⎪⎪⎪⎪⎪⎪
⎬
0
0
0
0
0
1
, L
sys D LD
−1/2
=
−1/2
=
I − D AD
−1/2
−1/2
=
−1
0
0
−1
0
⎪⎪⎪⎪⎪⎪⎧ 2
⎨
⎩⎪⎪⎪⎪⎪⎪
⎪⎪⎪⎪⎪⎪⎪⎧ 1
⎩⎪⎪⎪⎪⎪⎪⎪
1
− 6
0
1
− 6
0
0
⎨
0
−1
2
−1
0
0
−1
3
−1
0
−1
0
1
− 6
1
1
− 6
0
1
− 9
0
0
0
−1
3
−1
−1
0
1
− 6
1
1
− 6
0
0
−1
−1
0
−1
3
0
1
− 6
0
1
− 6
1
1
− 9
1
− 3
0
0
0
−1
0
⎪⎪⎪⎪⎪⎪⎫
1 ⎭⎪⎪⎪⎪⎪⎪
⎬
0
1
− 9
0
1
− 9
1
0
⎪⎪⎪⎪⎪⎪⎪⎫
⎭⎪⎪⎪⎪⎪⎪⎪
⎬
0
0
0
1
− 3
0
1
可以看出，标准归一化的拉普拉斯矩阵还是对称的，并且符合前面的公式定义。
Graph Convolution与Diffusion相似之处，当然从Random walk normalized Laplacian就能看出了两者确有相似之处（其实两者只差一个
相似矩阵的变换，可参考Diffusion-Convolutional Neural Networks)
其实维基本科对Laplacian matrix的定义上写得很清楚，国内的一些介绍中只有第一种定义。这让我在最初看文献的过程中感到一些的困
惑，特意写下来，帮助大家避免再遇到类似的问题。
3.2 无向图的拉普拉斯矩阵有什么性质
（1）拉普拉斯矩阵是半正定矩阵。（最小特征值大于等于0）
（2）特征值中0出现的次数就是图连通区域的个数。
（3）最小特征值是0，因为拉普拉斯矩阵（普通形式：
向量；
（4）最小非零特征值是图的代数连通度。
L = D − A
拉普拉斯矩阵的半正定性证明,如下：
要证明拉普拉斯矩阵是半正定的，只需要证明其二次型
证明：
T
f Lf ≥
0
）每一行的和均为0，并且最小特征值对应的特征向量是每个值全为1的
f LfT
T
T
T
= f Df − f Af
= f ∗ diag(d) ∗ f − f Af
f ∗ a ]f
ij
j
2
d f −
i i
=
T
j
m
∑
i=1
f ∗ f ∗ a
i
j
ij
[
m
∑
j=1
m
∑
i,j=1
2
d f −
i i
m
∑
i=1
m
∑
i=1
1
= [
2
=
=
1
2
m
∑
i=1
m
∑
i,j=1
2
d f − 2
i i
m
∑
i,j=1
f f a +
i j
ij
m
∑
j=1
2
d f ]
j
j
a (f − f )
ij
j
i
2
所以，对于任意一个属于实向量
f ∈ Rm
(f为m∗1的实数列向量 )，都有此公式成立：
T
f Lf =
1
2
m
∑
i,j=1
a (f −
ij
i
2
f )j
3.3 为什么GCN要用拉普拉斯矩阵？
拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解）
由于卷积在傅里叶域的计算相对简单，为了在graph上做傅里叶变换，需要找到graph的连续的正交基对应于傅里叶变换的基，因此
要使用拉普拉斯矩阵的特征向量。
3.4. 拉普拉斯矩阵的谱分解（特征分解）
GCN的核心基于拉普拉斯矩阵的谱分解，文献中对于这部分内容没有讲解太多，初学者可能会遇到不少误区，所以先了解一下特征分
解。
特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方
法。只有对可对角化矩阵或有n个线性无关的特征向量的矩阵才可以施以特征分解。
不是所有的矩阵都可以特征分解，其充要条件为n阶方阵存在n个线性无关的特征向量。
但是拉普拉斯矩阵是半正定矩阵（半正定矩阵本身就是对称矩阵），有如下三个性质：
对称矩阵一定n个线性无关的特征向量
半正定矩阵的特征值一定非负
对阵矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。
由上拉普拉斯矩阵对称知一定可以谱分解，且分解后有特殊的形式。
对于拉普拉斯矩阵其谱分解为：
L = UΛU =−1 U
⎡λ1 ⋱
⎣
⎤
λn⎦
−1
U
其中
U = (
u1 u2
,
, ⋯ ,
un
)
，是列向量为单位特征向量的矩阵，也就说 是列向量，Λ是n个特征值构成的对角阵。
ul
由于 U 是正交矩阵，即
UU =T
E
,所以特征分解又可以写成：
L = UΛU =−1 UΛU T
注意，特征分解最右边的是特征矩阵的逆，只是拉普拉斯矩阵是对称矩阵才可以写成特征矩阵的转置。
3.5 拉普拉斯算子
定义：拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子，定义为梯度（ ）的散度（
的实函数，则f的拉普拉斯算子∆定义为：
∇f
∇ ⋅ f
，即
∇f ⋅ f
）。因此如果f是二阶可微
f的拉普拉斯算子也是笛卡尔坐标系xi中的所有非混合二阶偏导数：
∆f = ∇ f =2
∇ ⋅ ∇f
∆f =
n
∑
i=1
∂ f2
2
∂xi
函数f的拉普拉斯算子也是该函数的海塞矩阵(是一个多元函数的二阶偏导数构成的方阵)的迹：
∆f = tr(H(f))
拉普拉斯算子(Laplacian operator) 的物理意义是空间二阶导，准确定义是：标量梯度场中的散度，一般可用于描述物理量的流入流出。
比如说在二维空间中的温度传播规律，一般可以用拉普拉斯算子来描述。
拉普拉斯矩阵也叫做离散的拉普拉斯算子。
4. 如何通俗易懂地理解卷积？
4.1 连续形式的一维卷积
在泛函分析中，卷积是通过两个函数f(x)和g(x)生成第三个函数的一种算子，它代表的意义是：两个函数中的一个(取g(x)，可以任意取)函
数，把g(x)经过翻转平移,然后与f(x)的相乘，得到的一个新的函数，对这个函数积分，也就是对这个新的函数求它所围成的曲边梯形的面
积。
设f(t),g(t)是两个可积函数，f(t)与g(t)的卷积记为
平移量的函数。也就是：
f(t) ∗ g(t)
，它是其中一个函数翻转并平移后与另一个函数乘积的积分，是一个自变量是
f(t) ∗ g(t) =
∫
+∞
−∞
f(τ)g(t −
τ)dτ =
∫
+∞
−∞
f(t −
τ)g(τ)dτ
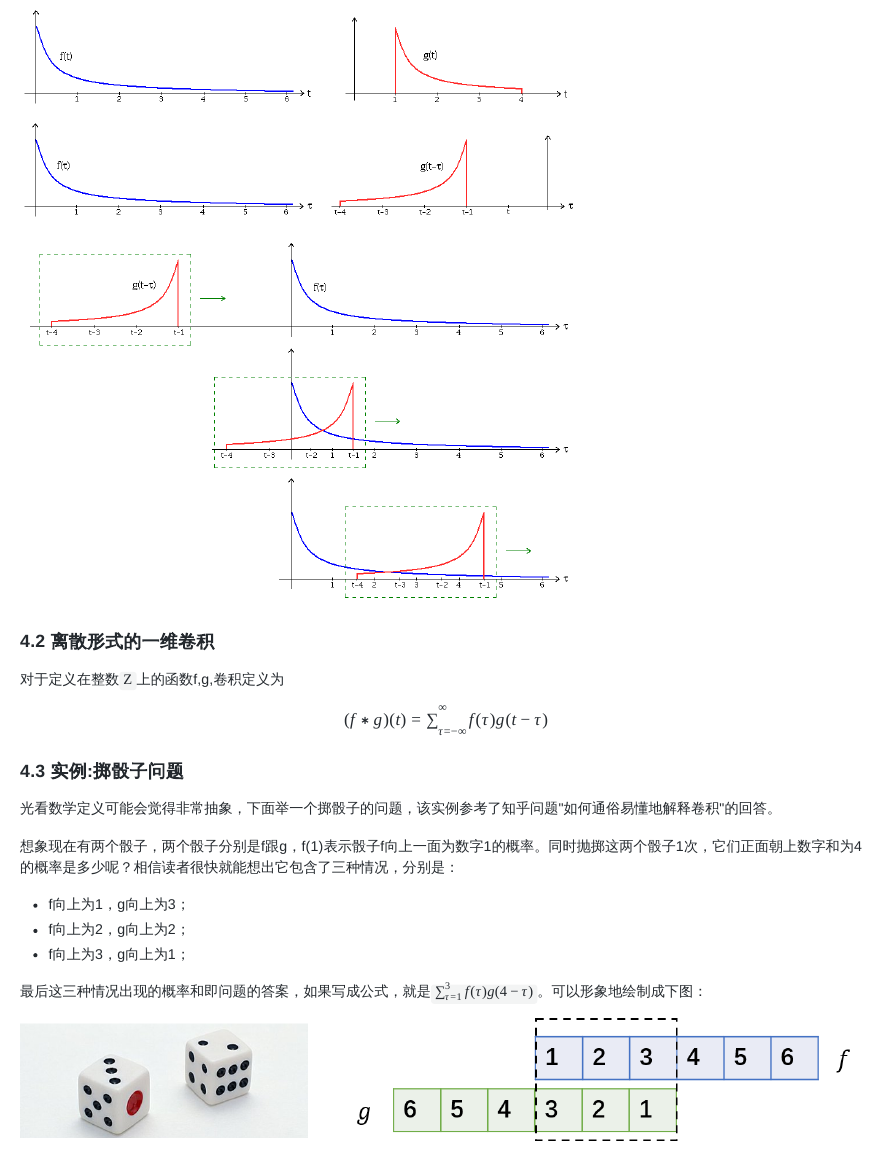
4.2 离散形式的一维卷积
对于定义在整数 上的函数f,g,卷积定义为
Z
4.3 实例:掷骰子问题
(f ∗ g)(t) =
∞
∑
τ=−∞
f(τ)g(t −
τ)
光看数学定义可能会觉得非常抽象，下面举一个掷骰子的问题，该实例参考了知乎问题"如何通俗易懂地解释卷积"的回答。
想象现在有两个骰子，两个骰子分别是f跟g，f(1)表示骰子f向上一面为数字1的概率。同时抛掷这两个骰子1次，它们正面朝上数字和为4
的概率是多少呢？相信读者很快就能想出它包含了三种情况，分别是：
f向上为1，g向上为3；
f向上为2，g向上为2；
f向上为3，g向上为1；
最后这三种情况出现的概率和即问题的答案，如果写成公式，就是
3
∑τ =1
f(τ)g(4 −
τ)
。可以形象地绘制成下图：
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
