2018年云南昆明理工大学现代设计理论考研真题.doc

发布时间：2022-09-16 发布人：admin 分类：说明书资料大小：0.05M 资料格式：doc 举报版权申诉

第1页 / 共2页

第2页 / 共2页

文本预览

2018 年云南昆明理工大学现代设计理论考研真题一、填空题：（每空 1 分，共 15 分） 1.无约束优化问题极值存在的必要条件是点处 2. 函数  , f x x 2 1   2 x 1  2 x 2  4 x x 1 2  在 5 X  0 T [2 4] 点处的梯度为矩阵 H 为 3.牛顿法和阻尼牛顿法最主要的区别是 , 充分条件是该，海赛。 4. 变尺度法的迭代公式为 xk+1=xk- αkHk ▽ f(xk) ，其中 Hk 必须满足的条件的是、、。 5.与梯度成锐角的方向为函数值方向，与负梯度成锐角的方向为函数值方向，与梯度成直角的方向为函数值方向。 6. 工程中常用的失效分布类型：、、、二、判断题（每题 2 分，共 10 分，对的打√，错的打ⅹ） 1.机械强度可靠性设计时应力-强度干涉理论中的“强度”是指机械零件的材料强度。（） 2.鲍威尔法会出现退化现象的根本原因是不能保证每轮迭代的搜索方向组中各搜索方向是线性无关的。（） 3.鲍威尔方法是一种直接方法、共轭方向法和坐标轮换法。（） 4.为了保证计算的精度，被分析对象的有限元模型必须和几何模型完全一致。（） 5.利用内点惩罚函数法可以求解含有等式约束的优化模型（）二、简答题：（每题 10 分，共 30 分） 1.试叙述有限元分析基本思想和主要步骤（10 分） 2.请简述数值迭代法的基本思想和关键问题（10 分） 3. 有人认为在进行机械结构设计中使用安全系数就是已经考虑了产品的可靠性，这种想法正确吗，为什么？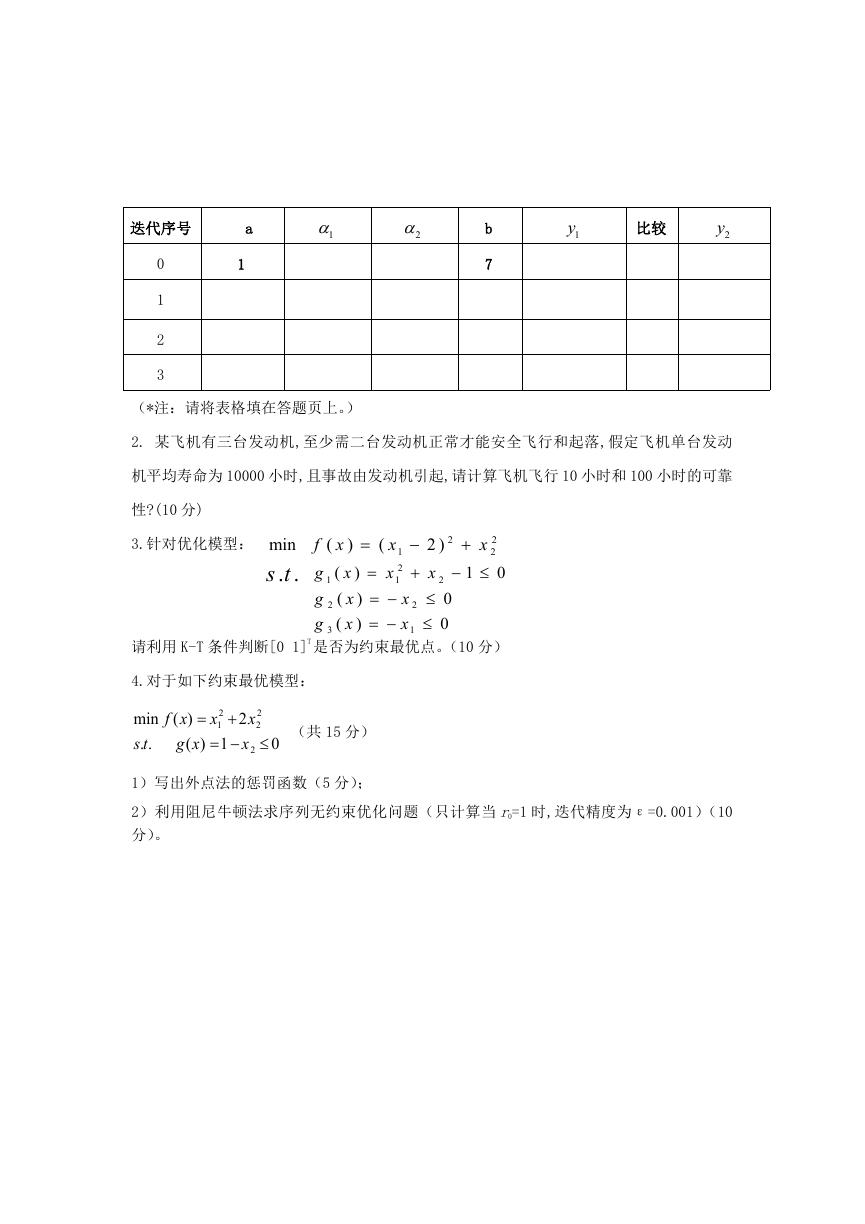（10 分）三、计算题：（45 分） 1、用黄金分割法求目标函数  f    2-6 +9  的极小值的计算过程，请完成（共 10 分）。

1 2 a 1 b 7 1y 比较 2y 迭代序号 0 1 2 3 （*注：请将表格填在答题页上。） 2. 某飞机有三台发动机,至少需二台发动机正常才能安全飞行和起落,假定飞机单台发动机平均寿命为 10000 小时,且事故由发动机引起,请计算飞机飞行 10 小时和 100 小时的可靠性?(10 分) 3.针对优化模型： min f g..ts g g ( 1 2 3 ) x ( x ( x ( x ( x  1 2 x  1   ) ) ) x x  1 2 2 x  0   2 1 2 )2 x    2 0 0 请利用 K-T 条件判断[0 1]T 是否为约束最优点。（10 分） 4.对于如下约束最优模型： 2 2 min ( ) x x f x   1 ( ) 1 . . g x x s t   2 2 2  0 （共 15 分） 1）写出外点法的惩罚函数（5 分）； 2）利用阻尼牛顿法求序列无约束优化问题（只计算当 r0=1 时,迭代精度为ε=0.001）（10 分）。

分享到：

赞收藏

资料库

2018年云南昆明理工大学现代设计理论考研真题.doc

相关推荐

考研

热门标签

最新资料