（中）popl95-基于图可达性的精确过程间数据流分析.pdf-资料库

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第1页.png

第1页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第2页.png

第2页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第3页.png

第3页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第4页.png

第4页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第5页.png

第5页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第6页.png

第6页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第7页.png

第7页 / 共31页

qq_39350874-12500474-（中）popl95-基于图可达性的精确过程间数据流分析.pdf-第8页.png

第8页 / 共31页

基于图形可达性的精确的过程间数据流分析 ThomasReps,SusanHorwitz,andMoolySagiv

摘要本文介绍了如何在多项式时间内，通过转化为一类特殊的图可达性问题，解决一大类程序间数据流分析问题，以实现精确求解。这种方法唯一的限制是数据流事实集必须是有限集，数据流函数必须分布在汇流运算符上（无论是并集运算还是交集运算）。这类问题包括-但不限于经典的可分离问题(也称为“gen/kill”或“位向量”问题)。例如，可达性问题，可用表达式问题和活变量问题（reachingdefifinitions,availableexpressions,andlivevariables）。此外，我们的技术处理的问题类别包括许多不可分离的问题，包括truly-live变量，复制常量传播，以及可能未初始化变量（truly-livevariables,copyconstantpropagation,andpossibly- uninitializedvariables）。结果是从C程序的初步实验研究中报告的（用于寻找可能的非初始化变量的问题）。 1. 导言本文介绍了如何在多项式时间内找到一大类过程间数据流分析问题的精确解。与进程内数据流分析中“精确”是指“满足所有路径”[20]不同的，一种精确的进程间数据流分析算法是指必须“满足所有有效路径”的解决方案。(如果满足这样一个事实，即当一个程序完成后，它返回到最近一次调用点[31，15，6，24，21，29]-见第2节，则说这个路径是有效的) 以往关于精确过程间数据流分析的相关工作可分为以下几类：  特定个体问题的多项式时间算法(例如。恒定传播[5，14]，流敏感摘要信息[6]和指针分析[24])。  一种用于有限类问题的多项式时间算法：局部可分问题(经典“位向量”或“gen/kill”问题的过程间版本 ) ，其中包括 reachingdefinitions 、 availableexpressions,andlivevariable[22]。  一类非常普遍的问题的算法[10，31，21]。第三类中引用的工作集中在一般性上，没有提供多项式时间算法。

与以前的工作相比，本文提供了一种多项式时间算法，用于寻找一般类过程间数据流分析问题的精确解。这个类包括所有的问题，其中数据流事实集D是一个有限的集合，数据流函数(在2D→2D中)分布在满足运算符上（无论是并集还是交集，取决于问题）。我们将把这类问题成为 “ 过程间有限分布子集问题 ” （Interprocedural,Finite,Distributive,Subsetproblem），或者简称为IFDS问题。所有的局部可分离问题(locallysparableproblem)都是IFDS问题。此外，许多不可分离的实际问题也是IFDS问题-例如：truly-livevariables[13]，copyconstantpropagation[12.pp.660]，以及 possibly-uninitializedvariables。我们的结果基于两个理解： 1) 通过限制域是原子数据流事实和数据流函数的幂集来分配，我们能够有效地创建简单的函数表示，总结过程的效果（通过支持从输入事实到输出事实的高效查找操作）。对于局部可分问题，摘要函数的表示是稀疏的。这允许我们的算法与以前针对这类问题的最有效的算法一样有效，但不会失去通用性。 2) 不是通过确定主循环的每次迭代成本并乘以迭代次数来计算我们算法的最坏情况成本，而是可以将算法的成本分解为三个贡献方面，并绑定为每个方面执行的操作的总成本（见附录）。我们工作最重要的方面可以总结如下：.  在第3节中，我们证明了所有的IFDS问题都可以通过将它们转化为一种特殊的图可达性问题来精确地解决：沿过程间可实现路径的可达性。与有向图中的普通可达性问题相反(例如，传递闭包），可实现路径可达性问题涉及一些考虑路径的约束。可实现路径模拟了调用返回结构的程序执行，并且只考虑“返回”可以与相应的 “调用”匹配的路径。  在第4节中，我们提出了一种新的多项式时间算法来解决可实现路径可达性问题。算法运行时间为O(ED3)；这个运行时间：比先前已知的该问题的最好算法渐近速度更快[16]。

 正如第5节所讨论的，新的可实现路径可达性算法是自适应的，当应用于具有受限形式的常见问题实例时，具有更好的渐近时间性能。例如，在局部可分问题的一般情况下，算法的性能有一个渐进改进。我们的工作概括了Knoop和Steffen[22]的工作，即我们的算法处理了一类更大的问题，但是在局部可分离的问题上，算法运行的时间与Knoop-Steffen算法的O(ED)时间相同。  对于过程间数据流分析问题的模糊（过于保守）答案可以通过处理每个过程间数据流分析问题来获得，就好像它本质上是一个大的过程内问题一样。在图可达性术语中，这相当于考虑所有路径，而不是只考虑过程间可实现的路径。对于IFDS问题，我们可以绑定所需的额外成本，以获得更精确的（可实现的路径）答案。在局部可分问题的重要特例中，根本没有“惩罚”-这两种解决方案都可以在时间O(ED) 中得到。在分配情况下，惩罚是D的一个因素：我们的可实现路径可达性算法的运行时间是O(ED3)，而所有路径的可达性解可以在时间O(ED2)中找到。然而，在第6节所报告的初步实验中，其中涉及D在70-142范围内的例子，观察到的惩罚最多为3.4倍。  Callahan给出了几种“过程间流敏感的副作用问题”的算法[6]。虽然这些问题（从某种技术角度）与IFDS数据流分析问题略有不同，但经过小的适应，第4节的算法可以应用于这些问题，并且比Callahan给出的算法渐近速度更快。此外，我们的算法处理Callahan的问题（这些问题是局部可分离的问题）的自然泛化到一类分配流敏感的副作用问题(这项工作和其他有关工作见第7节)。  可实现路径可达性问题也是进程间程序切片问题的核心，而该问题最快的先前已知算法是Horwitz、Reps和Binkley[16]给出的算法。本文所描述的可实现路径可达性算法得到了一种改进的过程间程序切片算法——其运行时间渐近快于Horwitz-Rep- Binkley算法。该算法的运行速度是Horwitz-Reps-Binkley算法的6倍[28]。  我们的数据流分析算法已经实现，并用于分析几个C程序。初步实验结果见第6 节。空间限制迫使我们以缩写形式对待上述一些材料。论文中所述所有定理的证明-

以及大量的补充材料，都可以在[27]中找到。

2.分配过程间数据流分析问题IFDS框架 IFDS框架是Sharir和Pnueli的“功能方法”的变体，用于过程间数据流分析[31]，其扩展类似于Knoop和Steffen给出的扩展，以便处理递归过程具有局部变量和参数的程序 [21]。这些框架将Kildall关于过程内数据流分析问题的“全路径满足”解决方案[20]的概念推广到过程间数据流分析问题的“全路径满足”解决方案。 IFDS框架的设计尽可能笼统（特别是支持有程序调用、参数以及全局和局部变量的语言）。在这个框架中可以指定的任何问题都可以使用我们的算法有效地解决；语义正确性是一个正交问题。希望利用我们的结果的问题设计者有两个义务：（Ⅰ)对问题进行编码，使其满足我们框架的条件；(Ⅱ）表明编码与编程语言的语义一致[9，10]。在IFDS框架中对问题进行编码可能会导致精度的损失。例如，在通过引用传递参数的语言中，存在别名的问题实例可能会失去精度。但是，找到IFDS问题的解决方案的过程不会带来精度的进一步损失。要指定IFDS框架，我们需要以下定义：定义2.1在IFDS框架中，程序a使用称为超图的有向图 G*=(N*，E*)表示。G*由流图集合G1，G2,···（每个程序一个）组成，其中一个， Gmain代表程序的主要程序。每个流程图Gp都有一个唯一的开始节点sp，和一个唯一的退出节点ep。流图的其他节点以通常的方式表示过程的语句和谓词，只是过程调用由两个节点表示，一个调用节点和一个返回点节点(过程p的调用和返回点节点集分别用 Callp和Retp表示；超图中所有调用和返回站点节点集分别用Call和Ret表示)。除了连接单个流图节点的普通过程内边外，对于每个程序调用，用调用节点c和返回点节点r表示，G*有三个边：  一种过程内的从c到r的“调用-返回点边”（call-to-return-siteedge）；  一种从c到程序调用开始节点的“过程间调用-开始边”（call-to-startedge）；  一种过程间的从程序退出点到r的“退出-返回点边”（exit-to-return-site）。

(call-to-return-site也包括在内，这样IFDS框架就可以处理带有本地变量和参数的程序。在call-to-return-site和exit-to-return-site边上的数据流函数允许有关保存在调用站点上的局部变量的信息与保存在被调用过程末尾的全局变量的信息相结合）。在讨论时间和空间需求时，我们使用集合的名称来表示集合的大小。例如，我们使用Call，而不是|Call|来表示图G中的调用节点数(我们与本约定有两个小的偏差，分别使用|N*|和|E*|)。例图1显示了一个示例程序及其超图G*。定义2.2一个长度为j的path从节点m到节点n的路径是一个j边的（可能是空的）序列，可以表示为[e1，e2，···，ej]，其中对于所有的i，1≤i≤j-1，边ei是边ei+1的来源。 “(程序间)有效路径”（interprocedurallyvalidpath）的概念抓住了这样一个概念:并不是G 中的所有路径都代表潜在的执行路径。定义2.3令G*中的每个调用节点都有一个惟一的索引i。对于每个这样的索引调用节点ci，用符号“(i”标记ci的call-to-start边出口；用符号“)i”标记相应的exit-to-return-site节点的入口。对于同一过程中的每一对节点m，n，从m到n的路径是一个相同同级有效路径，如果路径中标记的边序列是由以下无上下文语法匹配的非终端生成的平衡括号语言中的字符串：对于超图G*中的每一对节点m,n，一条从m到n的路径是一个有效路径，如果路径中标记边的序列是一个由非终结符产生的语言字符串，在以下语法中是有效的(在这里匹配的定义如上所示): 我们用IVP(m，n)表示从m到n的所有有效路径的集合。 *无效路径例子（译注）：

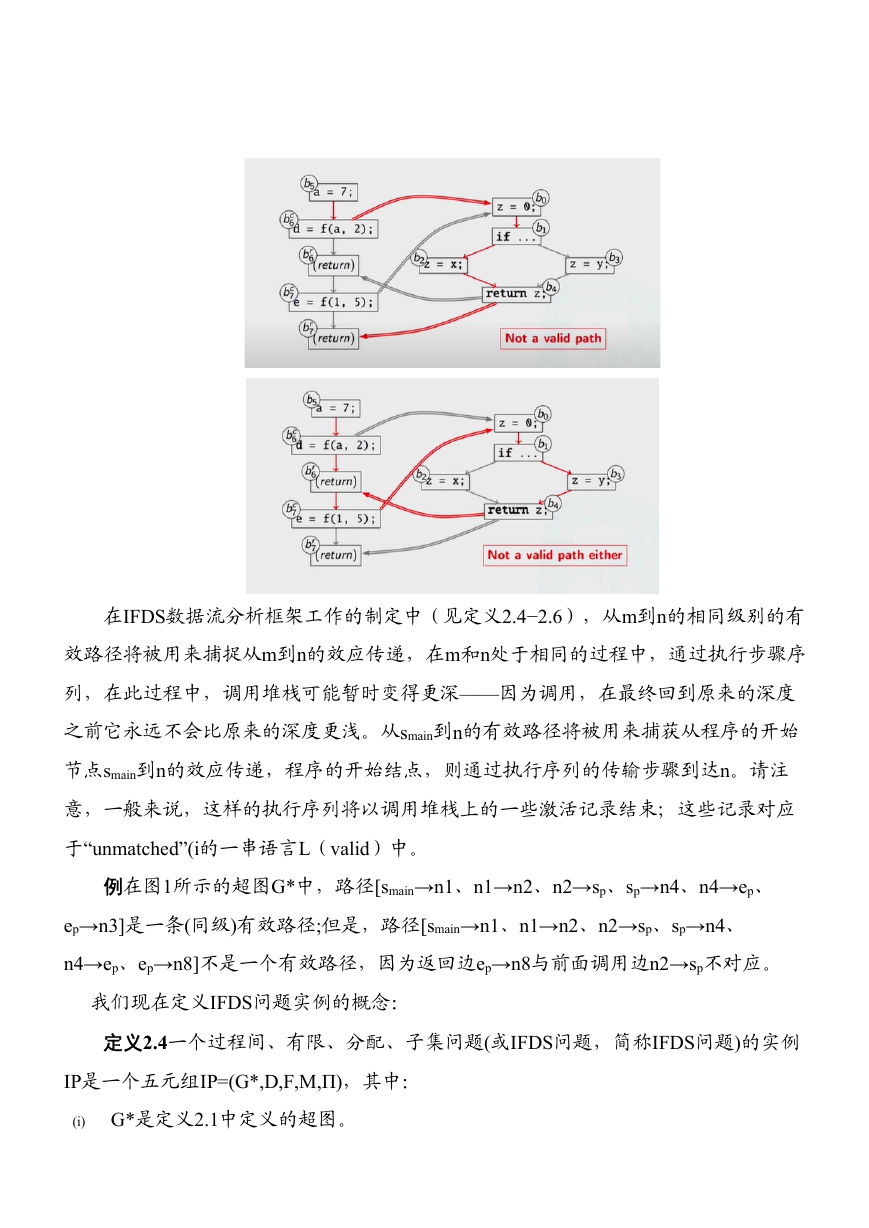
在IFDS数据流分析框架工作的制定中（见定义2.4−2.6），从m到n的相同级别的有效路径将被用来捕捉从m到n的效应传递，在m和n处于相同的过程中，通过执行步骤序列，在此过程中，调用堆栈可能暂时变得更深——因为调用，在最终回到原来的深度之前它永远不会比原来的深度更浅。从smain到n的有效路径将被用来捕获从程序的开始节点smain到n的效应传递，程序的开始结点，则通过执行序列的传输步骤到达n。请注意，一般来说，这样的执行序列将以调用堆栈上的一些激活记录结束；这些记录对应于“unmatched”(i的一串语言L（valid）中。例在图1所示的超图G*中，路径[smain→n1、n1→n2、n2→sp、sp→n4、n4→ep、 ep→n3]是一条(同级)有效路径;但是，路径[smain→n1、n1→n2、n2→sp、sp→n4、 n4→ep、ep→n8]不是一个有效路径，因为返回边ep→n8与前面调用边n2→sp不对应。我们现在定义IFDS问题实例的概念：定义2.4一个过程间、有限、分配、子集问题(或IFDS问题，简称IFDS问题)的实例 IP是一个五元组IP=(G*,D,F,M,П)，其中： (i) G*是定义2.1中定义的超图。

资料库

（中）popl95-基于图可达性的精确过程间数据流分析.pdf

相关推荐

课程资源

热门标签

最新资料