第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
BP神经网络逼近非线性函数.doc
一、试论述人工神经网络的特点及发展概况
答：人工神经网络是利用物理器件来模拟生物神经网络的某些结构和功能；即从
人脑的生理结构出发，来研究人的智能行为，模拟人脑的信息处理能力；从
而反映了人脑功能若干基本特征，如并行处理、学习、联想、模式分类等。
神经网络的主要特点有：并行分布处理；
非线性映射；
通过训练进行学习；
适应与集成；
硬件实现等。
人工神经网络的发展概况：
1、兴起阶段：
(1)早在 1943 年，心理学家 McCulloch 和数学家 Pitts 总结了生物神经元的一些
基本生理特性，提出了形式神经元的数学描述与结构方法，即 M—P 模型：
y
；它的提出兴起了对神经网络的研究。
Sgn
(
j
xw
ji
i
j
)
i
(2)1949 年心理学家 D．O．Hebb 提出神经元之间突触联系强度可变的假设。他
认为学习过程是在突触上发生的，突触的联系强度随其前后神经元的活动而变
化。根据这一假设提出的学习率为神经网络的学习算法奠定了基础。即：
w
ij
i
(0
i
x
i
(
k
)
x
j
(
k
()
i
j
)
j
)
(3)1958 年，Rosenblatt 提出了感知机，第一次把神经网络的研究付诸工程实践。
2、萧条阶段：
主要的影响因素：
(1)60 年代，美国著名人工智能学者 Minsky 和 Papert 对 Rosenblatt 的工作进
行了深入的研究，写了很有影响的《感知机》一书，指出感知机的处理能力有限，
甚至连 XOR 这样的问题也不能解决，并指出如果引入隐含神经元，增加神经网络
的层次，可提高神经网络的处理能力，但是研究对应的学习方法非常困难。
(2)那时人工智能的以功能模拟为目标的另一分支，出现了转机，产生了以知识
信息处理为基础的知识工程，给人工智能从实验室走向实用带来了希望。
(3)微电子技术的发展，使传统计算机的处理能力有很大提高，数字计算机的发
展使当时科技界普遍认为它能解决一切问题，包括模式识别、机器人控制等，因
而不必去寻找新的计其理论与实现方法。
(4)当时的工艺水平还未能达到制作实用的具有足够规模的神经网络，用分离的
电子管即使是晶体管所制作的神经网络也只能作示教性的表演。
3、兴盛阶段：
主要研究成果：
1982 年，美国物理学家 J.Hopfield 提出了 Hopfield 网络模型，在研究中
他引入了能量函数，阐明了神经网络与动力学的关系；并用非线性动力学的方法
来研究网络特性，从而建立了神经网络稳定性判据；并指出信息存储在网络中神
经元之间的连接上；这一成果的取得使神经网络的研究取得了突破性进展。
1984 年， Hopfield 设计与研制了他所提出的神经网络模型的电路，并指出
网络中的每一神经元可以用运算放大器来实现，所有神经元的连接可以用电子线
路来模拟，这—方案为神经网络的工程实现指明了方向。同时在应用研究上，他
成功地解决了旅行商(TSP)问题，引起了人们的震惊。
1986 年 D.E.Rumelhart 和 J.L.Mcclelland 等人提出了多层网络反向传播算
法,简称 BP 网络;该算法可用来解决函数逼近等问题。
Hopfield 网和反向传播算法的提出使人们看到了神经元网络的前景和希
望；1987 年在美国召开了国际神经网络会议，它掀起了神经网络研究的热潮。
二、试给出实现图 2-1 所示模式分类的感知器网络，其中，“○”表示 1，“×”
表示 0。
图 2-1
图 2-2
感知器中， )1(
1 、 )1(
2 和 )1(
3 为隐层中的三个神经元， )2(
1 是一个起逻辑“与非”
作用的位于输出层的神经元。其中，
0
1 , XX
0
2
为输入，第一层有三个神经元，每
一个的输出分别是 1
1X 、 1
2X 、 1
3X ，第二层为输出层， 2
1X 为输出，
输入输出变换关系为：
q
)
(
i
q
)
(
Sf
(
i
)
3,2,1
q
1
1
2,1
(
S
i
S
q
)
q
(
i
0
)
0
S
(
q
)
i
2
j
1
(
q
)
w
ij
x
j
(
q
)1
x
i
从图 2-1 中可以看出，每个点对应于 L1 、L2 、L3 的输出为（在线的上面的点输
出为 1，在线下面的点输出为-1）：
1～3 点均为（1 -1 1）
4～8 点均为（-1 -1 -1）
9～11 点均为（-1 1 1）
12 点为（1 1 1）
a b c d 为（-1 -1 1）
这显然是一个三维空间，建立如下图所示坐标系：
这样就可以把“○”和“×”分开。红点即为“○”，黄点即为“×”。于是可以
图 2-3
找一个平面把红点和黄点分开，即可设计出 W(2)
13、 )2(
1 。
11、W(2)
12、W(2)
三. 试用 BP 神经网络逼近非线性函数
f(u) =
)5.0u(9.1e
sin(10u)
其中，u[-0.5,0.5]
%输入样本
u=-0.5:0.01:0.5;
a=exp(-1.9*(u+0.5));
b=sin(10*u);
y=a.*b;
plot(u,y);
title('要逼近的非线性函数');
xlabel('time');
ylabel('unlinear function');
%使用 newff 函数创建前馈神经网络，初始化的权值和阈值为零，隐层采用正切 S 型神经元，
输出层采用线形神经元
net = newff(minmax(u),[5,1],{'tansig' 'purelin'} ,'trainlm');
%绘出目标函数图象
%给出题头
%X 轴的标注
%Y 轴的标注
%目标函数输出
y1 = sim(net,u);
figure;
plot(u,y, u,y1,'r')
%绘出目标函数图象和未经训练的网络逼近函
数
%给出题头
%X 轴的标注
%Y 轴的标注
%训练次数
%性能函数值
%网络训练
%绘出目标函数图象，未经训练的网络逼近函数
original-');
title('没有训练的网络仿真结果');
xlabel('time');
ylabel('simulating output--
legend('要逼近的非线性函数','未训练的网络输出');
net.trainParam.epochs=60;
net.trainParam.goal=0.001;
net =train(net,u,y);
figure;
y2 = sim(net,u);
plot(u,y, u,y1,'r',u,y2,'g--')
和训练的网络逼近函数
title('training result');
xlabel('time');
ylabel('output of simulating');
legend('要逼近的非线性函数','未训练的网络输出','训练后的网络输出');
%给出题头
%X 轴的标注
%Y 轴的标注
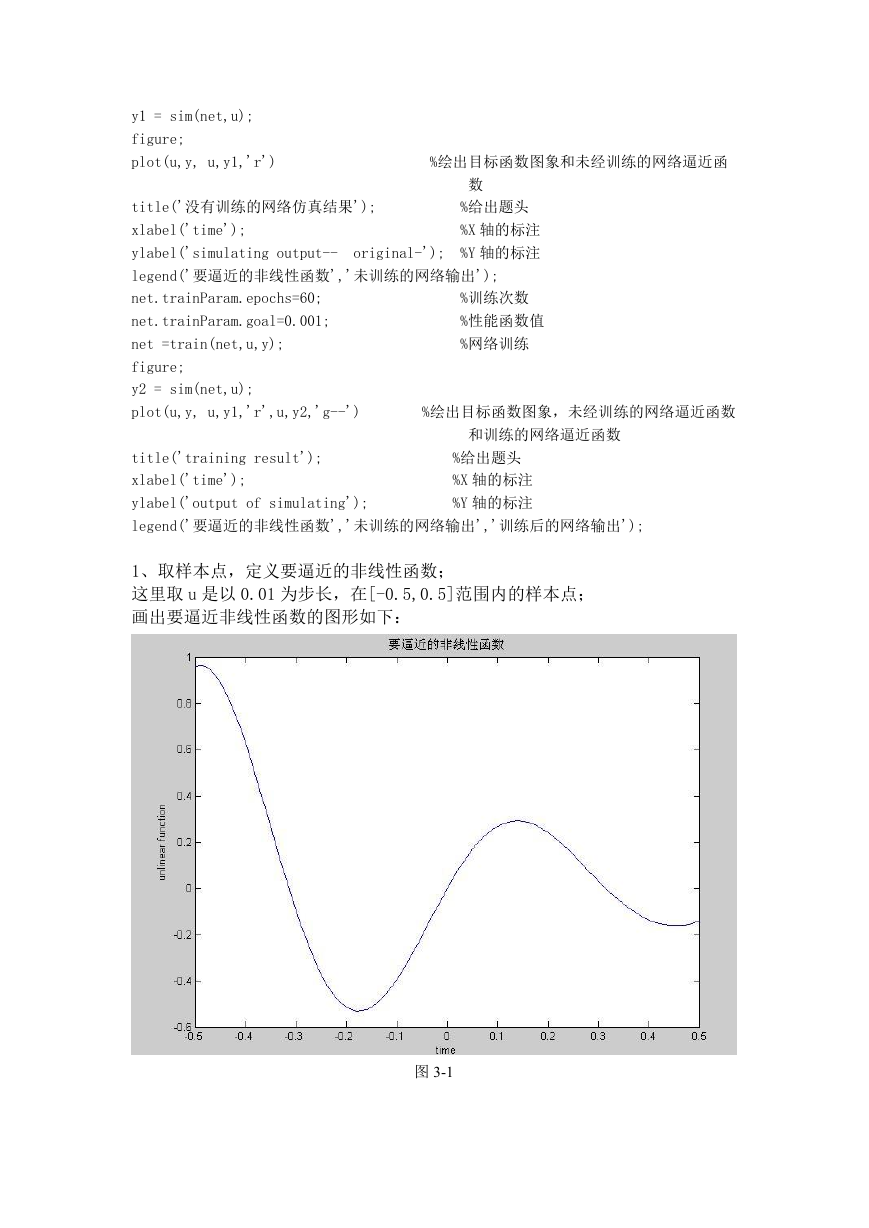
1、取样本点，定义要逼近的非线性函数；
这里取 u 是以 0.01 为步长，在[-0.5,0.5]范围内的样本点；
画出要逼近非线性函数的图形如下：
图 3-1
2、建立相应的 BP 神经网络
MATLAB 中，使用函数 newff 建立 BP 网络，本题中采用双层网络，选择各神经单
元的传递函数分别为 tansig 函数和 purelin 函数，设置 BP 网络反向函数为
trainlm。
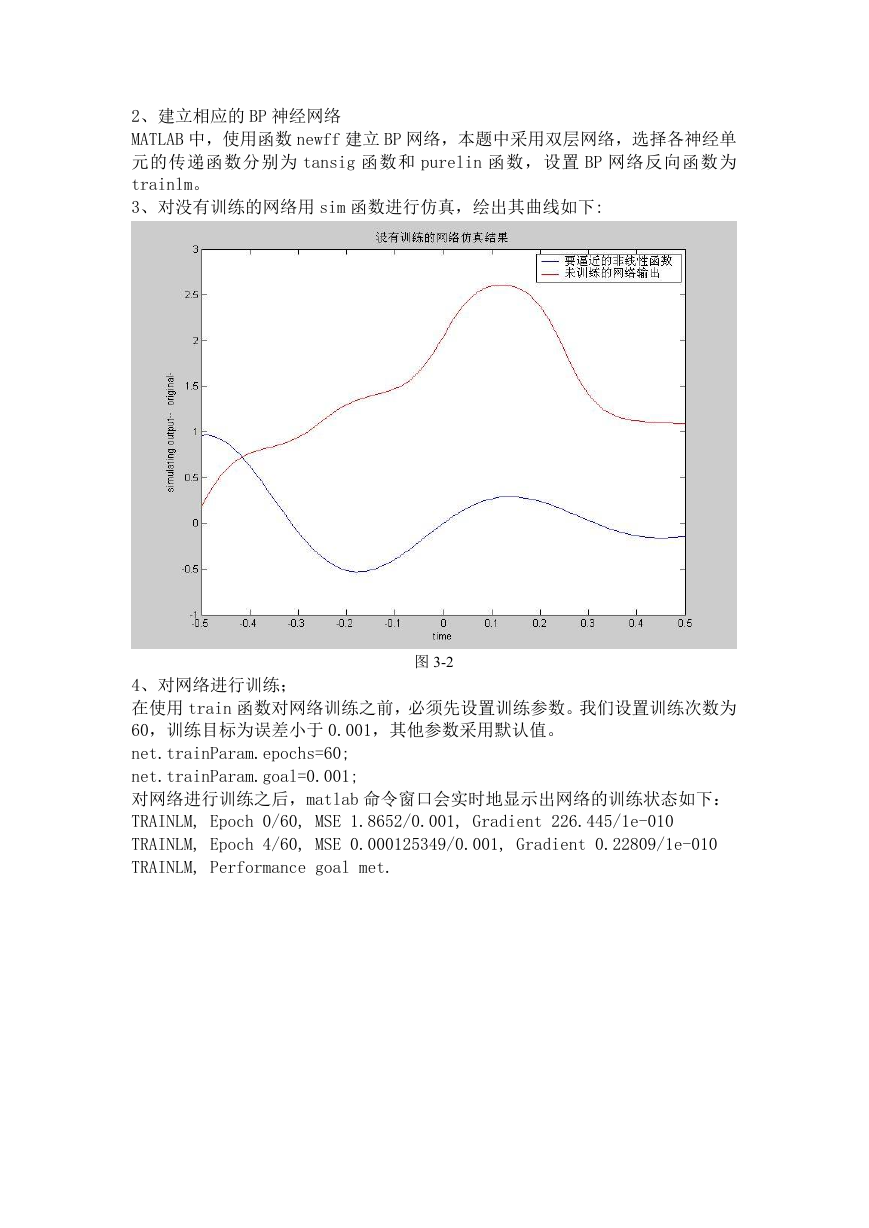
3、对没有训练的网络用 sim 函数进行仿真，绘出其曲线如下:
图 3-2
4、对网络进行训练；
在使用 train 函数对网络训练之前，必须先设置训练参数。我们设置训练次数为
60，训练目标为误差小于 0.001，其他参数采用默认值。
net.trainParam.epochs=60;
net.trainParam.goal=0.001;
对网络进行训练之后，matlab 命令窗口会实时地显示出网络的训练状态如下：
TRAINLM, Epoch 0/60, MSE 1.8652/0.001, Gradient 226.445/1e-010
TRAINLM, Epoch 4/60, MSE 0.000125349/0.001, Gradient 0.22809/1e-010
TRAINLM, Performance goal met.
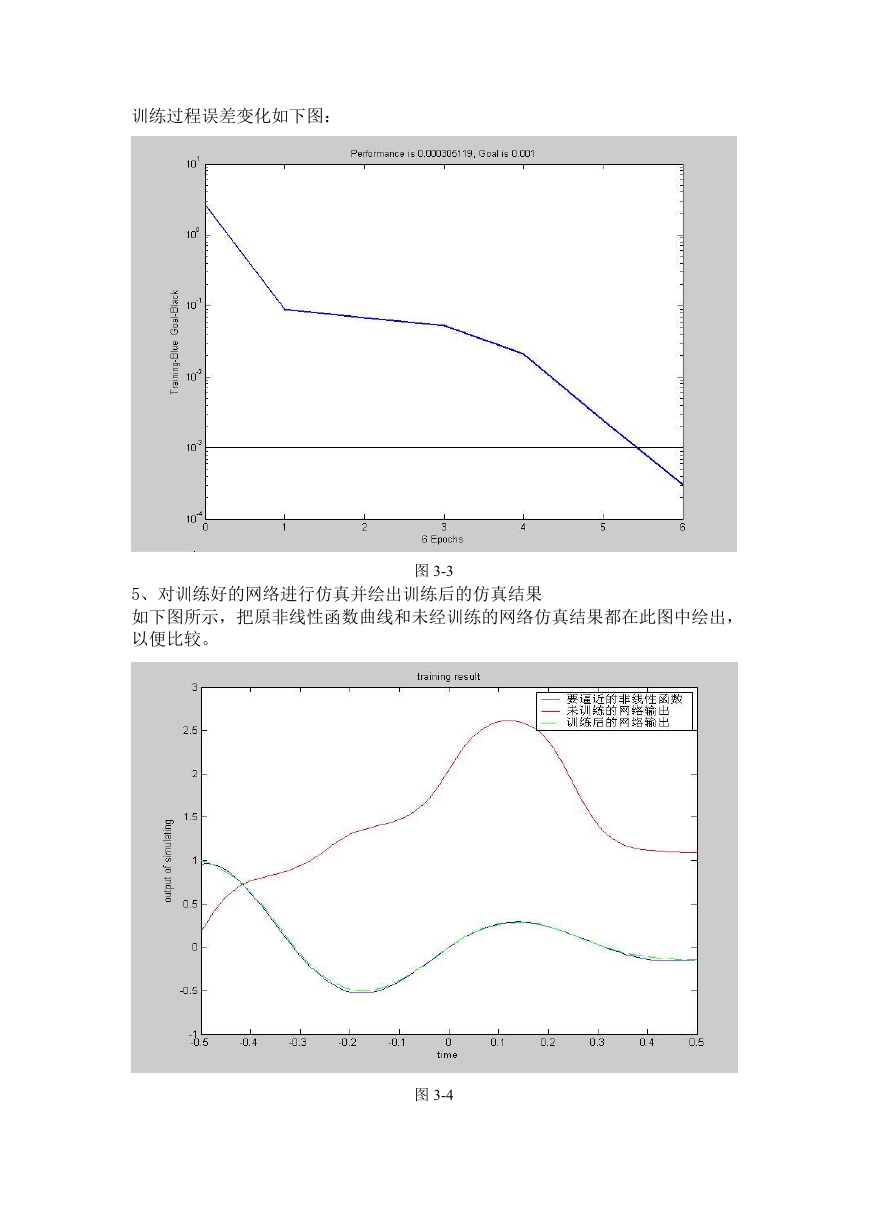
训练过程误差变化如下图：
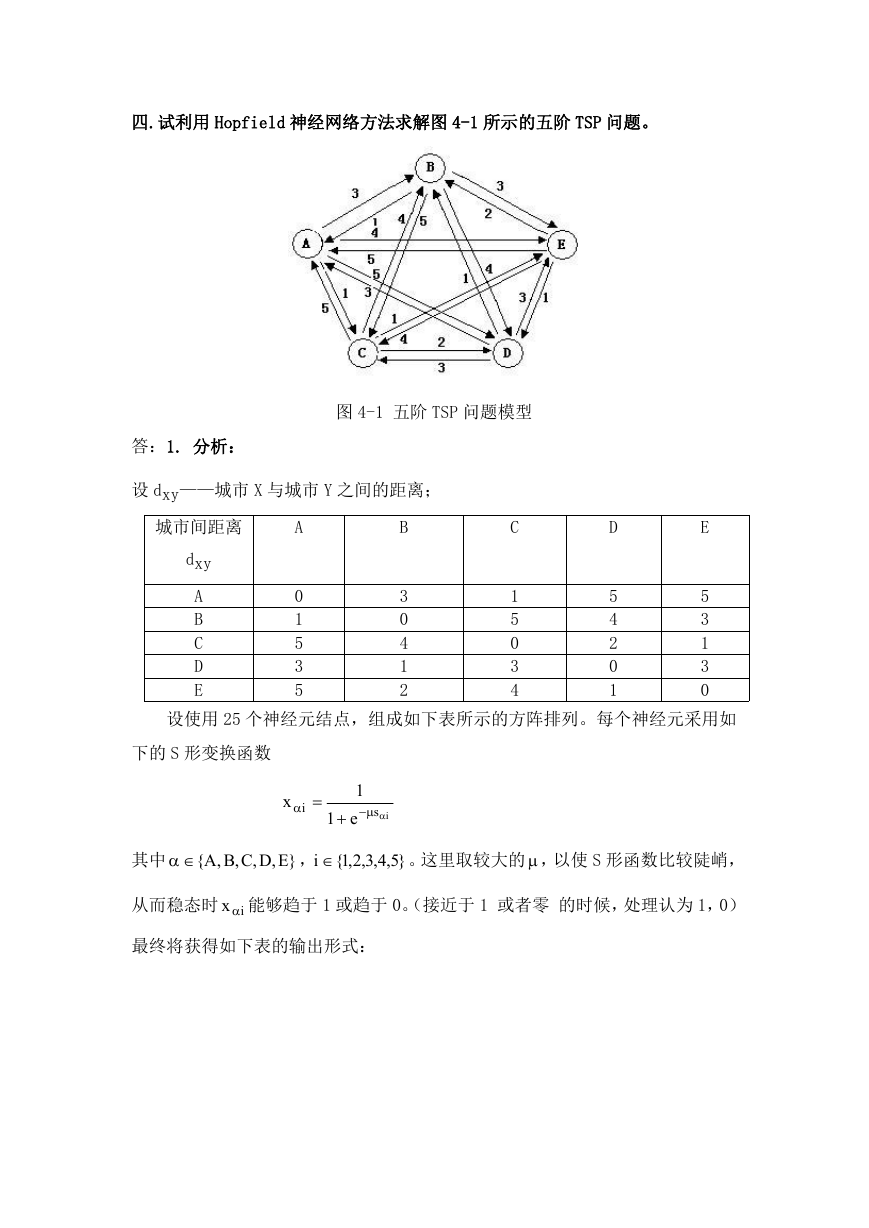
5、对训练好的网络进行仿真并绘出训练后的仿真结果
如下图所示，把原非线性函数曲线和未经训练的网络仿真结果都在此图中绘出，
以便比较。
图 3-3
图 3-4
四.试利用 Hopfield 神经网络方法求解图 4-1 所示的五阶 TSP 问题。
图 4-1 五阶 TSP 问题模型
答：1. 分析：
设 dxy——城市 X 与城市 Y 之间的距离；
城市间距离
dxy
A
B
C
D
E
A
0
1
5
3
5
B
3
0
4
1
2
C
1
5
0
3
4
D
5
4
2
0
1
E
5
3
1
3
0
设使用 25 个神经元结点，组成如下表所示的方阵排列。每个神经元采用如
下的 S 形变换函数
x
i
1
is
e1
其中
}E,D,C,B,A{
，
}5,4,3,2,1{i
。这里取较大的 ，以使 S 形函数比较陡峭，
从而稳态时 ix 能够趋于 1 或趋于 0。（接近于 1 或者零 的时候，处理认为 1，0）
最终将获得如下表的输出形式：
城市名
A
B
C
D
E
1
0
1
0
0
0
访问顺序标示
3
1
0
0
0
0
4
0
0
0
0
1
5
0
0
1
0
0
2
0
0
0
0
1
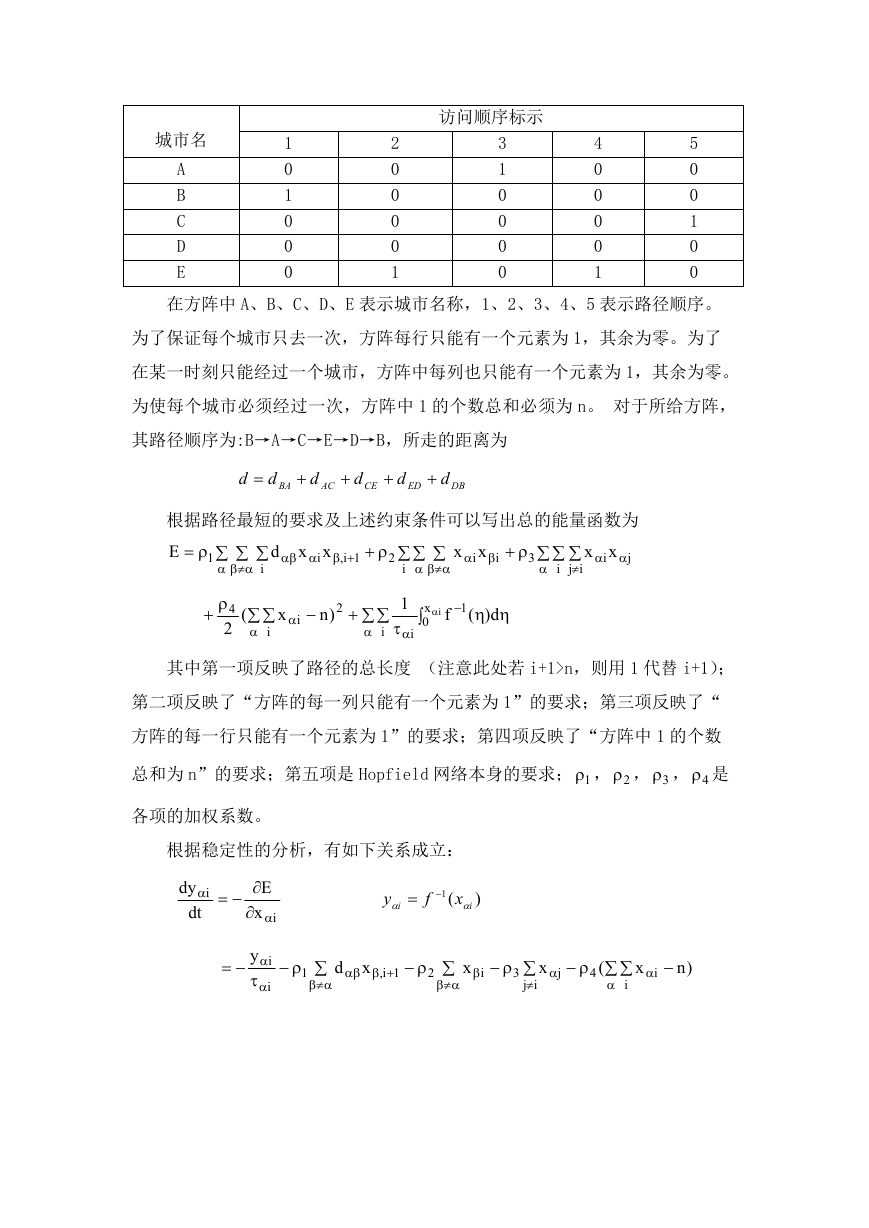
在方阵中 A、B、C、D、E 表示城市名称，1、2、3、4、5 表示路径顺序。
为了保证每个城市只去一次，方阵每行只能有一个元素为 1，其余为零。为了
在某一时刻只能经过一个城市，方阵中每列也只能有一个元素为 1，其余为零。
为使每个城市必须经过一次，方阵中 1 的个数总和必须为 n。 对于所给方阵，
其路径顺序为:B→A→C→E→D→B，所走的距离为
d
d
BA
d
AC
d
CE
d
ED
d
DB
根据路径最短的要求及上述约束条件可以写出总的能量函数为
E
d
xx
1i,
i
xx
i
xx
i
j
1
2
i
i
i
3
ij
i
4
2
(
i
x
i
2
)n
1
i
i
ix
0
f
1
d)(
其中第一项反映了路径的总长度 （注意此处若 i+1>n，则用 1 代替 i+1）；
第二项反映了“方阵的每一列只能有一个元素为 1”的要求；第三项反映了“
方阵的每一行只能有一个元素为 1”的要求；第四项反映了“方阵中 1 的个数
总和为 n”的要求；第五项是 Hopfield 网络本身的要求； 1 ， 2 ， 3 ， 4 是
各项的加权系数。
根据稳定性的分析，有如下关系成立：
i
dy
dt
E
x
i
y
i
f
(1
x
i
)
y
i
i
1
d
x
1i,
2
x
i
ij
3
x
j
(
4
i
x
i
)n
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
