2XXX 年 X 月 第 X 卷 第 X 期 doi：10. 19665/j.issn.1001-2400.2XXX.0X.0 西安电子科技大学学报 JOURNAL OF XIDIAN UNIVERSITY Xxx.2XXX Vol.XX No.X 对 ABY3 框架的专题研究报告 肉夹馍1 (1. 西安电子科技大学 网络与信息安全学院，陕西 西安 710071) 摘要：本文研究了一个关于隐私保护的机器学习通用框架，该框架先分析加法和乘法的秘密共享方案， 在此基础上研究共享十进制值的不动点乘法、矩阵乘法、评估分段多项式函数的定制协议以及 ABY 之 间的转换，并用其运用到线性回归、logistic 回归和神经网络模型。协议是在一个三服务器模型中，数据 所有者在三个服务器之间秘密共享他们的数据，这些服务器使用三方计算（3PC）对联合数据上的模型 进行训练和评估。 关键词：机器学习；3PC；秘密共享 文献标识码：A 中图分类号： 文章编号：1001-2400(2XXX)0X-0-0 1 调研对象 本文研究的论文来自 CCS 2018 年的一篇会议，论文题目：ABY3: A Mixed Protocol Framework for Machine Learning(ABY3：一种用于机器学习的混合协议框架)，作者是 Peter Rindal 和 Payman Mohassel。 2 问题与安全需求 技术的更新与实现，缩小了大量工作的处理时间。但是用于机器学习的 MPC 技术主要局限于两个服 务器模型，并不能从这些加速中获益，而且大部分方案针对的是较弱的半诚实攻击者的安全。所以作者研 究的是三服务器模型下的隐私保护机器学习，但是这个场景不仅仅只限于三方。 然而，直接将新的 3PC 技术应用到机器学习算法上，并不能为隐私保护机器学习加速。 ·第一个挑战是 3PC 技术只适用于 Z2k 环上的计算。而在机器学习计算中，训练数据和中间参数都是 十进制值，不能使用模运算进行本地处理。 ·第二个挑战是，大多数机器学习过程需要在算术运算（如乘法和加法）和非算术运算（如近似激活 函数（如 logistic 函数）和分段多项式函数（如 RELU））之间来回切换。不同共享类型之间转换成本高昂， 且性能也需考虑在内。 3 前人工作及研究现状 前人在决策树、k-均值聚类、支持向量机分类、线性回归和 logistic 回归上的隐私保护机器学习都有研 究。这些论文提出了基于安全多方计算的解决方案，但由于没有充分利用 MPC 的最新进展和缺乏实现， 且开销成本较大。 3.1 线性回归 Nikolaenko 等人提出了使用线性同态加密(LHE)和混淆电路的组合进行的水平分割数据上的隐私保护 线性回归协议，并在具有数百万个样本的数据集上评估它。Gascon 等人将结果扩展到竖直分割数据，并表 现出更好的性能。但是，这两篇文章都将问题缩小到使用姚氏混淆电路协议求解线性系统，这使得训练时 间的开销较大且无法应用于非线性模型。该篇文章中，使用随机梯度下降（SGD）方法进行训练，这种方 法产生更快的协议，并且能够训练非线性模型，例如神经网络。Mohassel 和 Zhang 最近的工作也使用 SGD ______________________________ 收稿日期： 基金项目： 作者简介： 网络出版地址： 网络出版时间： 

2 西安电子科技大学学报 第 XX 卷 进行训练，使用算术、布尔和 Yao 共享 2PC 的混合（通过 ABY 框架）。他们还介绍了一种新的近似不动 点乘法方法，该方法避免了截断小数的布尔运算，并产生了用于训练线性回归模型的最新性能。以上仅限 于双服务器模型，没涉及该文提到的 3PC 模型。Gilad Bachrach 等人提出了一个支持隐私保护线性回归的 框架。然而，由于大量使用混淆电路，该框架的伸缩性不好。 3.2 logistic 回归 Wu 等人考虑了隐私保护的 logistic 回归。他们提出用多项式逼近 logistic 函数，用 LHE 训练模型。然 而，复杂度在近似多项式的程度上呈指数级。Aono 等人考虑一个不同的安全模型，其中一个不受信任的服 务器从多个客户端收集并组合加密的数据，并将其传输到一个受信任的客户端，以在明文上训练该模型。 但是，在此设置中，聚合数据的明文将泄漏给训练模型的客户端。 3.3 神经网络 Shokri 和 Shmatikov 提出了一种解决方案，两台服务器在训练期间共享部分系数的变化。虽然该系统 非常高效（完全不需要加密操作），但这些系数变化容易泄露。 Riazi 等人和 Liu 等人每个人都对 ABY 框架提出了效率改进，并将其用于隐私保护神经网络推理。 Chandran 等人提出了一个自动编译程序为 ABY 组件的框架，并说明了如何使用它来评估神经网络模型。 这些构造都基于两方协议，并且由于新的 3PC 技术而没有从主要的加速中获益。它们也只为半诚实的对手 提供安全保障。 Mohassel 和 Zhang 为此定制了 ABY 框架，提出了一种新的避免布尔电路的近似定点乘法协议，并用 它训练神经网络模型。他们的定点乘法技术仅限于 2PC。 4 课本思路 首先 3PC 可衍生到 MPC，大概率情况下会用上 secret share，尤其是在机器学习模型和隐私保护中，也 就意味着联邦学习能够可以采取这一系列思路。对于训练线性回归模型，只需要使用算术共享，即加法复 制共享。但是，在逻辑回归和神经网络训练中，也通用需要执行需要位级运算的计算。一般用是使用布尔 共享，即加法共享或 3PC 姚共享。前者的通信效率更高，但轮数与电路深度成正比；后者轮数较少，而通 信成本较高。 关 于 ABY 框 架 可 参 考 Demmler 等 人 的 ABY - A framework for efficient mixed-protocol secure two-partycomputation 论文中提到的 ABY 框架。 5 Paper 的最终思路 5.1 加法 首先我们需要知道 ABY 的三种共享的形式，分别是： x 1 x 1 LSB Arithmetic : Boolean . :. CGYao   x   x   x x   3 x  3 x   x 2 x 2 ( x 1 : B A Y ) 2 加密数据采用的是复制秘密共享技术。 通过对三个随机值 x 、、 1 x 3 x 2 kZ 2 进行采样，使得 x  x 1  x 2  x 3 ，他们共享一个秘密值 2 。这些 share 以对   kZx 被表示为 Ax 。比如有一些算法搜索共享，若想把它们中的两个 x 和 y 加起来，在本地进行相应的share 的形式分配，其中第 i 方持有第 i 对。这样的共享将 , xx 3 2 , xx 3 , xx 1  1   ,   , 2 加法，得到总和的新 share，即 z i  x i  y i 。 http://journal.xidian.edu.cn/xdxb 

第 X 期 5.2 乘法 对 ABY3 框架的专题研究报告 3 乘法的情况实际上更复杂，不能仅仅在本地做个乘法共享的 iz ，这样会丢失交叉积。该文使用了一种 称为复制的秘密共享的方案，即双方不持有三个shares 中的一个share，而是持有三个shares 中的两个shares。 每一方都可以计算一些交叉项的子集。这样每一方都能在本地计算出一个新的 share iz 。 y 2  y 3 )  xy     ( x 1 yx 11 yx 12 yx 13 x      2 yx 21 yx 2 yx 3 )( y x 1 3 yx  31 yx  2 yx  33 2 3 2 yx 31 yx 2 yx 3 yx  13 yx  12 yx  33 2 2 z 1 z z 2 3    yx 11 yx 21 yx 2 3    这样，第一方有 1 1, yx 出 2z 后给第三方，第三方有 和 2, yx 3 和 3, yx 2 ，自行求出 1z 后给第二方，第二方有 1 1, yx 和 2, yx 2 ，自行求 3, yx 3 ，自行求出 3z 后给第一方。这样每个点都有两个本地shares， 可进行乘法计算。 5.3 定点乘法 做乘法运算时，实际上会遇到一个问题，得到的数字位数是原来的两倍。简单的可以直接删掉底部和 顶部部分，可能会在底部得到一些舍入误差，可能会在顶部的字节上舍入。此文提出一种方法，其主要思 想是，简单地切换到一种有两个秘密共享的类型，然后切换回去并执行此操作。 m   : preprocess r Z  2       ' z x y      ' reveal t z     ' 2/ t z r   .1 .2 .3 l   ' r    r l 2/    r  首先，预处理一个随机值r ，它是双方共享的秘密。最开始计算 'r ，它和r 是同一个版本，但是底部 的l 位被截断了，这个部分在预处理阶段可实现。在联机阶段做传统的乘法协议。现在就有两 shares，t 和 'r ， l t 2/ 有点像第一个 share，而 'r 像是第二个 share。该方法最终几乎没有传统整数乘法的开销，并 且可以支持定点计算。 5.4 矩阵乘法 有一个二维矩阵 X 和一个向量 Y，把它们相乘得到 Z。按照传统的矩阵乘法算法，取每一行和每一列， 计算内积就得到了相应的元素，形成一个矩阵。这样做的通信开销很大。再看到前边的乘法，首先计算所 有这些矩阵项的本地 share iz ，这个内积，然后只传达最终结果 iz ，在最后一次计算出结果。 5.5 分段多项式 在机器学习算法中，会对当前数据应用非线性函数。多方计算技术不能很好地处理指数类型的除法， 但是激活函数通常会使用这些除法。该文用近似的方法来代替这些传统的方法。 http://journal.xidian.edu.cn/xdxb 

4 西安电子科技大学学报 第 XX 卷 首先按阈值 it 将函数或目标函数划分为 0, f 和 ，评估多项式性能的策略是取和。 f f 2 1     xf 1 m   i  0    x  t i   x  t      x f i i 1  中间的括号部分是一个范围查询，验证 x 是否在 it 到 1it 的两个范围内，然后把值乘以相应的函数， 最后把它们加起来。一般使用传统的 MPC 技术可以很容易地计算出这些多项式 if ，可以得出哪个是好的。 问题在于，如何计算这个范围查询边界是否是公共的，然而要查的内容是私人或秘密的。 B  x  t i  b i  c i   B     Convert Most  Converty  to  significan   t i bit binary     t i arithmetic t   x   x      1  b b i i B  to  首先取阈值 it ，然后减去 x，再采用 binary seeker Shane 方案。在这个 binary secret Shane 方案 中，最重要的有效位实际上是作为符号位的。通过转换为 Boolean secret Shane，就可以立即有用的符号 位。在最终与 if 多项式的乘法运算之前，需要把它转换回 arithmetic seeker Shane 格式。 5.6 线性回归 机器学习算法中的线性回归是给定一些点，找到一条直线穿过它们，直线和点之间的偏差最小。试图 找到一个线性函数 f ，因为 f 是线性的，所以可以把它表示为输入 ix 的内积，每个维度都有相应的权重。 我们试图找到使距离目标 y 最小的权重。 x  11  x  21  ...  x     ，    x 1 d x 2 d ... x x 12 x 22 ... x y 1 y 2 ... y ... ... ... ...             X   y nd 1 n 2 n n 迭代权重定义为： w j (   w  j ) xywX ij  i i ，括号部分是某种预测值输出-真正的标签，再乘以误 差方向和学习率，最终会收敛到最优w 。这些乘法运算就可用上上方的矩阵乘法。 5.7 logistic 回归 logistic 回归在线性回归的基础上再往前走一步，即判断分类。相比于计算线性回归： ww  1 B X  T B  ( X  Yw B ) B logistic 回归需要计算： ww  1 B ((  X  T B X B  ) Yw B  ) ，  )( z  1  e z 1 这里的函数将一种任意值映射到 0 和 1，解决分类问题。但是它是非线性的，并不适用于 MPC。所 http://journal.xidian.edu.cn/xdxb 

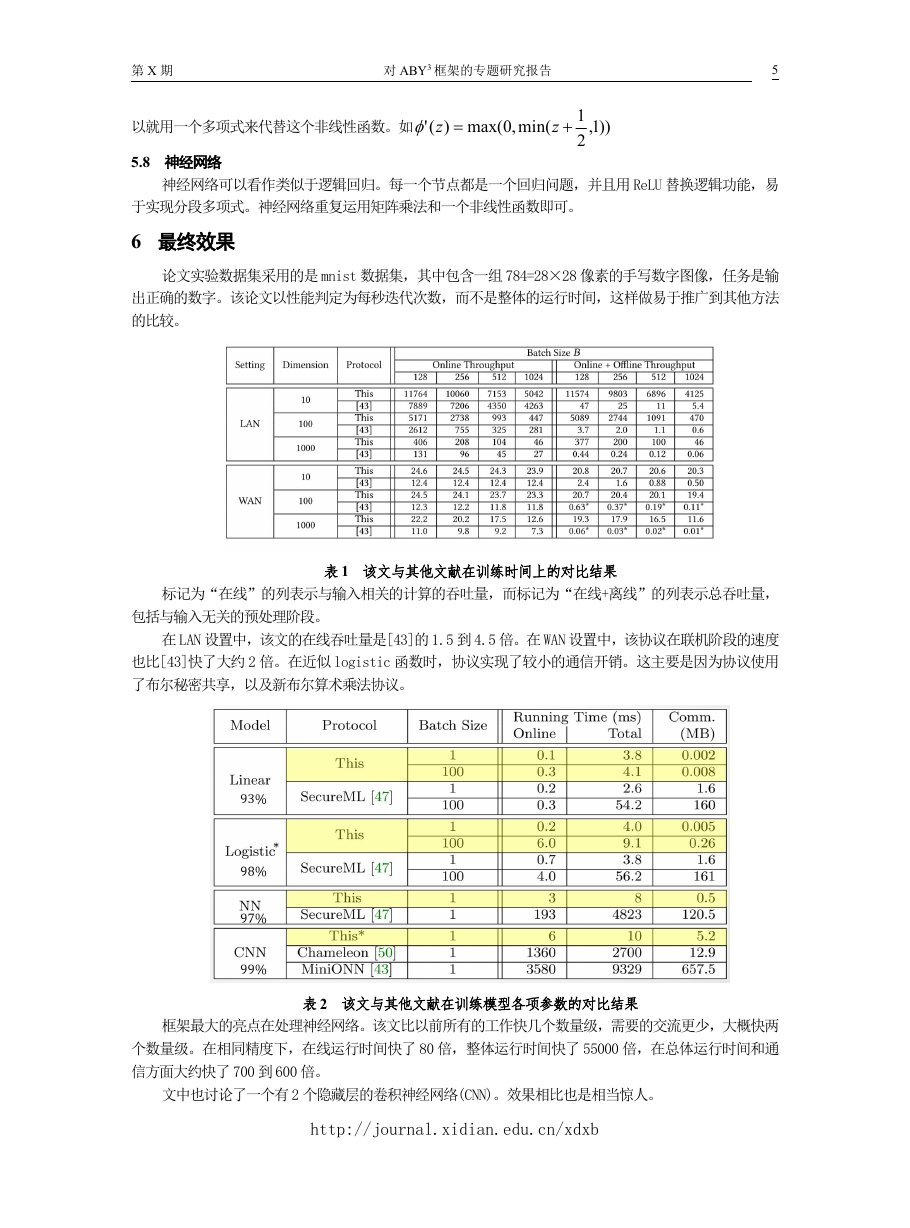
第 X 期 对 ABY3 框架的专题研究报告 5 以就用一个多项式来代替这个非线性函数。如 )(' z  ,0max( min( z  5.8 神经网络 1 2 ))1, 神经网络可以看作类似于逻辑回归。每一个节点都是一个回归问题，并且用 ReLU 替换逻辑功能，易 于实现分段多项式。神经网络重复运用矩阵乘法和一个非线性函数即可。 6 最终效果 论文实验数据集采用的是 mnist 数据集，其中包含一组 784=28×28 像素的手写数字图像，任务是输 出正确的数字。该论文以性能判定为每秒迭代次数，而不是整体的运行时间，这样做易于推广到其他方法 的比较。 标记为“在线”的列表示与输入相关的计算的吞吐量，而标记为“在线+离线”的列表示总吞吐量， 表 1 该文与其他文献在训练时间上的对比结果 包括与输入无关的预处理阶段。 在 LAN 设置中，该文的在线吞吐量是[43]的 1.5 到 4.5 倍。在 WAN 设置中，该协议在联机阶段的速度 也比[43]快了大约 2 倍。在近似 logistic 函数时，协议实现了较小的通信开销。这主要是因为协议使用 了布尔秘密共享，以及新布尔算术乘法协议。 表 2 该文与其他文献在训练模型各项参数的对比结果 框架最大的亮点在处理神经网络。该文比以前所有的工作快几个数量级，需要的交流更少，大概快两 个数量级。在相同精度下，在线运行时间快了 80 倍，整体运行时间快了 55000 倍，在总体运行时间和通 信方面大约快了 700 到 600 倍。 文中也讨论了一个有 2 个隐藏层的卷积神经网络(CNN)。效果相比也是相当惊人。 http://journal.xidian.edu.cn/xdxb