High Performance Discrete Fourier Transforms on
Graphics Processors
Naga K. Govindaraju, Brandon Lloyd, Yuri Dotsenko, Burton Smith, and John Manferdelli
{nagag,dalloyd,yurido,burtons,jmanfer}@microsoft.com
Microsoft Corporation
Abstract—We present novel algorithms for computing discrete
Fourier transforms with high performance on GPUs. We present
hierarchical, mixed radix FFT algorithms for both power-of-two
and non-power-of-two sizes. Our hierarchical FFT algorithms
efficiently exploit shared memory on GPUs using a Stockham
formulation. We reduce the memory transpose overheads in
hierarchical algorithms by combining the transposes into a block-
based multi-FFT algorithm. For non-power-of-two sizes, we use a
combination of mixed radix FFTs of small primes and Bluestein’s
algorithm. We use modular arithmetic in Bluestein’s algorithm
to improve the accuracy. We implemented our algorithms using
the NVIDIA CUDA API and compared their performance with
NVIDIA’s CUFFT library and an optimized CPU-implementation
(Intel’s MKL) on a high-end quad-core CPU. On an NVIDIA
GPU, we obtained performance of up to 300 GFlops, with typical
performance improvements of 2–4× over CUFFT and 8–40×
improvement over MKL for large sizes.
I. INTRODUCTION
The Fast Fourier Transform (FFT) refers to a class of
algorithms for efficiently computing the Discrete Fourier
Transform (DFT). The FFT is used in many different fields
such as physics, astronomy, engineering, applied mathematics,
cryptography, and computational finance. Some of its many
and varied applications include solving PDEs in computational
fluid dynamics, digital signal processing, and multiplying large
polynomials. Because of its importance,
the FFT is used
in several benchmarks for parallel computers such as the
HPC challenge [1] and NAS parallel benchmarks [2]. In this
paper we present algorithms for computing FFTs with high
performance on graphics processing units (GPUs).
The GPU is an attractive target for computation because of
its high performance and low cost. For example, a $300 GPU
can deliver peak theoretical performance of over 1 TFlop/s
and peak theoretical bandwidth of over 100 GiB/s. Owens et
al. [3] provides a survey of algorithms using GPUs for general
purpose computing. Typically, general purpose algorithms for
the GPU had to be mapped to the programming model pro-
vided by graphics APIs. Recently, however, alternative APIs
have been provided that expose low-level hardware features
that can be exploited to provide significant performance gains
[4], [5], [6], [7]. In this paper we target NVIDIA’s CUDA API,
though many of the concepts have broader application.
Main Results: We present algorithms used in our library
for computing FFTs over a wide range of sizes. For smaller
sizes we compute the FFT entirely in fast, shared memory.
For larger sizes, we use either a global memory algorithm or
a hierarchical algorithm, depending on the size of the FFTs
and the performance characteristics of the GPU. We support
non-power-of-two sizes using a mixed radix FFT for small
primes and Bluestein’s algorithm for large primes. We address
important performance issues such as memory bank conflicts
and memory access coalescing. We also address an accuracy
issue in Bluestein’s algorithm that arises when using single-
precision arithmetic. We perform comparisons with NVIDIA’s
CUFFT library and Intel’s Math Kernel Library (MKL) on a
high end PC. On data residing in GPU memory, our library
achieves up to 300 GFlops at factory core clock settings,
and overclocking we achieve 340 GFlops. We obtain typical
performance improvements of 2–4× over CUFFT and 8–
40× over MKL for large sizes. We also obtain significant
improvements in numerical accuracy over CUFFT.
The rest of the paper is organized as follows. After dis-
cussing related work in Section II we present an overview
of mapping FFT computation to the GPU in Section III. We
then present our algorithms in Section IV and implementation
details in Section V. We compare results with other FFT
implementation in Section VI and then conclude with some
ideas for future work.
II. RELATED WORK
A large body of research exists on FFT algorithms and
their implementations on various architectures. Sorensen and
Burrus compiled a database of over 3400 entries on efficient
algorithms for the FFT [8]. We refer the reader to the book
by Van Loan [9] which provides a matrix framework for
understanding many of the algorithmic variations of the FFT.
The book also touches on many important implementation
issues.
The research most related to our work involves accelerating
FFT computation by using commodity hardware such as GPUs
or Cell processors. Most implementations of the FFTs on the
GPU use graphics APIs such as current versions of OpenGL
or DirectX [10], [11], [12], [13], [14], [15]. However, these
APIs do not directly support scatters, access to shared memory,
or fine-grained synchronization available on modern GPUs.
Access to these features is currently provided only by vendor-
specific APIs. NVIDIA’s FFT library, CUFFT [16], uses the
CUDA API [5] to achieve higher performance than is possible
with graphics APIs. Concurrent work by Volkov and Kazian
[17] discusses the implementation of FFT with CUDA. We
also use CUDA for FFTs, but we handle a much wider range
of input sizes and dimensions.
�
Fig. 1. Architecture and programming model on the NVIDIA GeForce 8800 GPU. On the left, we illustrate a high-level diagram of the GPU scalar processors
and memory hierarchy. This GPU has 128 scalar processors and 80 GiB/s peak memory bandwidth. On the right, we illustrate the programming model for
scheduling computation on GPUs. The data in the GPU memory is decomposed into independent thread blocks and scheduled on the multiprocessors.
Several researchers have examined the implementation of
the FFT on the Cell processor [18], [19], [20], [21], [22].
Our results for large sizes on commodity GPUs are generally
higher than published results for the Cell for large sizes.
III. OVERVIEW OF GPUS AND FFTS
A. Overview of GPUs
In this paper we focus primarily on NVIDIA GPUs, al-
though many of the principles and techniques extend to other
architectures as well. Fig. 1 highlights the hardware model
of a NVIDIA GeForce 8800 GPU. The GPU consists of a
large number of scalar, in-order processors that can execute the
same program in parallel using threads. Scalar processors are
grouped together into multiprocessors. Each multiprocessor
has several fine-grain hardware thread contexts, and at any
given moment, a group of threads called a warp, executes
on the multiprocessor in lock-step. When several warps are
scheduled on a multiprocessor, memory latencies and pipeline
stalls are hidden primarily by switching to another warp. Each
multiprocessor has a large register file. During execution,
the program registers are allocated to the threads scheduled
on a multiprocessor. Each multiprocessor also has a small
amount of shared memory that can be used for communication
between threads executing on the scalar processors. The GPU
memory hierarchy is designed for high bandwidth to the global
memory that
is visible to all multiprocessors. The shared
memory has low latency and is organized into several banks
to provide higher bandwidth.
At a high-level, computation on the GPU proceeds as
follows. The user allocates memory on the GPU, copies the
data to the GPU, specifies a program that executes on the
multiprocessors and after execution, copies the data back to
the host. In order to execute the program on a domain, the
user decomposes the domain into blocks. The thread execution
manager then assigns threads to operate on the blocks and
write the output to global memory.
B. Overview of FFTs
N−1
The forward Discrete Fourier Transforms (DFT) of a
N−1
complex sequence x = x0, . . . , xN−1
is an N-point
complex sequence, X = X0, . . . , XN−1, where Xk =
j=0 xje−2πijk/N . The inverse DFT is similarly defined
as xk = 1
j=0 Xje2πijk/N . A na¨ıve implementation of
N
DFTs requires O(N 2) operations and can be expensive. FFT
algorithms compute the DFT in O(N log N) operations. Due to
the lower number of floating point computations per element,
the FFT can also have higher accuracy than a na¨ıve DFT. A
detailed overview of FFT algorithms can found in Van Loan
[9]. In this paper, we focus on FFT algorithms for complex
data of arbitrary size in GPU memory.
C. Mapping FFTs to GPUs
Performance of FFT algorithms can depend heavily on the
design of the memory subsystem and how well it is exploited.
Although GPUs provide a high degree of memory parallelism,
the index-shuffling stage (also referred to as bit-reversal for
radix-2) of FFT algorithms such as Cooley-Tukey can be
quite expensive due to incoherent memory accesses. In this
paper, we avoid the index-shuffling stage using Stockham
formulations of the FFT. This, however, requires that we
perform the FFT out-of-place. Fig. 2 shows pseudo-code for
a Stockham radix-R FFT with specialization for radix-2. In
each iteration, the algorithm can be thought of combining the
R FFTs on subsequences of length Ns into the FFT of a new
sequences of length RNs by performing an FFT of length R
on the corresponding elements of the subsequences.
The performance of traditional GPGPU implementations of
FFT using graphics APIs is limited by the lack of scatter
operations, that is, a thread cannot write to an arbitrary location
in memory. The pseudo-code shown in Fig. 2 writes to R
different locations each iteration (line 29). Without scatter,
R values must be read for each output generated rather than
MultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPGPU MemoryProblem DomainThread BlockRegsRegsRegsShared MemoryThread BlockRegsRegsRegsShared MemoryThread Execution ManagerMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPMultiprocessorShared MemorySPSPSPSPSPSPSPSPSPSPSPSPSPSPSPSPGPU MemoryDRAMDRAMDRAMDRAMDRAMDRAM�
reading R values for every R outputs [14]. GPUs and APIs
that support writing multiple values to the same location in
multiple buffers can save the redundant reads, but must either
use more complex indexing when accessing the values written
in a preceding iteration, or after each iteration, they must
copy the values to their proper location in a separate pass
[15], which consumes bandwidth. Thus scatter is important
for conserving memory bandwidth.
Fig. 2 also shows pseudo-code for an implementation of the
FFT on a GPU which supports scatter. The main difference
between GPU_FFT() and CPU_FFT() is that the index j
into the data is generated as a function of the thread number
t, the block index b, and the number of threads per block T
(line 13). Also, the iteration over values of Ns are generated
by multiple invocations of GPU_FFT() rather than in a loop
(line 3) because a global synchronization between threads is
needed between the iterations, and for many GPUs the only
global synchronization is kernel termination.
Despite the fact
that GPU_FFT() uses scatter,
For each invocation of GPU_FFT(), T is set to N/R and
the number of thread blocks B is set to M, where M is the
number of FFTs to process simultaneously. Processing multi-
ple FFTs at the same time is important because the number
of warps used for small-sized FFTs may not be sufficient to
achieve full utilization of the multiprocessor or to hide memory
latency while accessing global memory. Processing more than
one FFT results in more warps and alleviates these problems.
it still
has a number of performance issues. First,
the writes to
memory have coalescing issues. The memory subsystem tries
to coalesce memory accesses from multiple threads into a
smaller number of accesses to larger blocks of memory. But
the space between consecutive accesses generated during first
few iterations (small Ns) is too large for coalescing to be
effective (line 29). Second, the algorithm does not exploit low-
latency shared memory to improve data reuse. This is also
a problem for traditional GPGPU implementations as well,
because the graphics APIs do not provide access to shared
memory. Finally, to handle arbitrary lengths, we would need
to write a separate specialization for all possible radices R.
This is impractical, especially for large R. In the next section
we will discuss how we address each of these issues.
Because GPUs vary in shared memory sizes, memory, and
processor configurations, the FFT algorithms should ideally
be parameterized and auto-tuned across different algorithm
variants and architectures.
IV. FFT ALGORITHMS
In this section, we present several FFT algorithms — a
global memory algorithm that works well for larger FFTs with
higher radices on architectures with high memory bandwidth, a
shared memory algorithm for smaller FFTs, a hierarchical FFT
that exploits shared memory by decomposing large FFTs into a
sequence of smaller ones, mixed-radix FFTs that handle sizes
that are multiples of small prime factors, and an implementa-
tion of Bluestein’s algorithm for handling larger prime factors.
Fig. 2. Reference implementation of the radix-R Stockham algorithm. Each
iteration over the data combines R subarray of length Ns into arrays of length
RNs. The iterations stop when the entire array of length N is obtained.
The data is read from memory and scaled by so-called twiddle factors (lines
20–25), combined using an R-point FFT (line 26), and written back out to
memory (lines 27–29). The number of threads used for GPU_FFT(), T , is
N/R. The expand() function can be thought of as inserting a dimension
of length N2 after the first dimension of length N1 in a linearized index.
We also discuss extensions to handle multi-dimensional FFTs,
real FFTs, and discrete cosine transforms (DCTs).
A. Global Memory FFT
As mentioned in Section III.B,
the pseudo-code for
GPU_FFT() in Fig. 2 can lead to poor memory access coa-
lescing, which reduces performance. On some GPUs the rules
for memory access coalescing are quite stringent. Memory
accesses to global memory are coalesced for groups of CW
threads at a time, where CW is the coalescing width. CW is
16 for recent NVIDIA GPUs. Coalescing is performed when
each thread in the group access either a 32-bit, 64-bit, or 128
bit word in sequential order and the address of the first thread
is aligned to (CW× word size). Bandwidth for non-coalesced
accesses is about an order of magnitude slower. Later GPUs
have more relaxed coalescing requirements. Coalescing is
performed for any access pattern, so long as all the threads
access the same word size. The hardware issues memory
transactions in blocks of 32, 64, or 128 bytes while seeking to
float2* CPU_FFT(int N, int R, 1 float2* data0, float2* data1) { 2 for( int Ns=1; Ns( v ); 26 int idxD = expand(j,Ns,R); 27 for( int r=0; r( float2* v ) { 32 float2 v0 = v[0]; 33 v[0] = v0 + v[1]; 34 v[1] = v0 - v[1]; 35 } 36 37 int expand(int idxL, int N1, int N2 ){ 38 return (idxL/N1)*N1*N2 + (idxL%N1); 39 } 40 �
Fig. 3.
Function for exchanging the R values in v between T threads.
The real and imaginary components of v are stored in separate arrays to
avoid bank-conflicts. The second synchronization avoids read-after-write data
hazards. The first synchronization is necessary to avoid data hazards only
when exchange() is invoked multiple times.
minimize the number and size of the transactions to satisfy the
requests. For both sets of coalescing requirements, the greatest
bandwidth is achieved when the accesses are contiguous and
properly aligned.
Assuming that the number of threads per block T = N/R
is no less than CW , our mapping of threads to elements in
the Stockham formulation ensures that the reads from global
memory are in contiguous segments of at least CW in length
(line 23 in Fig. 2). If the radix R is a power of two, the
reads are also properly aligned. Writes are not contiguous
for the first logR CW iterations where Ns < CW (line
29), although under the assumption that T ≥ CW , when
all the writes have completed, the memory areas touched do
contain contiguous segments of sufficient length. Therefore,
we handle this problem by first exchanging data between
threads using shared memory so that it can then be written
out in larger contiguous segments to global memory. We do
this by replacing lines 28–29 with the following:
The pseudo-code for exchange() can be found in Fig. 3.
To maximize the reuse of data read from global memory
and to reduce the total number of iterations, it is best to use
a radix R that is as large as possible. However, the size of
R is limited by the number of registers and the size of the
shared memory on the multiprocessors. Reducing the number
of threads reduces the total number of registers and the amount
of shared memory used, but with too few threads there are not
enough warps to hide memory latency. We have found that
using T = max(64Ri, N/R) produces good results, where
xRi represents the smallest power of R not less than x.
Bank conflicts: Shared memory on current GPUs is orga-
nized into 16 banks with 32-bit words distributed round-
robin between them. Accesses to shared memory are serviced
for groups of 16 threads at a time (half-warps). If any of
the threads in a half-warp access the same memory bank
Fig. 4.
Pseudo-code for shared memory radix-R FFT. This kernel is used
when N is small enough that the entire FFT can be performed using just
shared memory and registers.
at the same time, a conflict occurs, and the simultaneous
accesses must be serialized, which degrades performance. In
order to avoid bank conflicts, exchange() writes the real
and imaginary components to separate arrays with stride 1
instead of a single array of float2. When a float2 is
written to shared memory, the two components are written
separately with stride 2, resulting in bank conflicts. The call
to exchange() still results in bank conflicts when R is a
power of two and Ns < 16. The solution is to pad with Ns
empty values between every 16 values. For R = 2 the extra
cost of computing the padded indexes actually outweighs the
benefit of avoiding bank conflicts, but for radix-4 and radix-
8, the net gain is significant. Padding requires extra shared
memory. To reduce the amount of shared memory by a factor
of 2, it is possible to exchange only one component at a time.
This requires 3 synchronizations instead of 1, but can result
in a net gain in performance because it allows more in-flight
threads. When R is odd, padding is not necessary because R
is relatively prime w.r.t. the number of banks.
B. Shared Memory FFT
For small N, we can perform the entire FFT using only
shared memory and registers without writing intermediate
results back to global memory. This can result in substan-
tial performance improvements. The pseudo-code for our
shared memory kernel
is shown in Fig. 4. As with the
global memory FFT, we set
the number of threads T to
T = max(64Ri, N/R). These lower bounds on the thread
count also ensure that when the data is read from global
memory (lines 4–6), it will be read in contiguous segments
void exchange( float2* v, int R, int stride, 1 int idxD, int incD, 2 int idxS, int incS ){ 3 float* sr = shared, *si = shared+T*R; 4 __syncthreads(); 5 for( int r=0, ; r void 1 FftShMem(int sign, int N, float2* data){ 2 float2 v[R]; 3 int idxG = b*N + t; 4 for( int r=0; r( v ); 26 int idxD = expand(j,Ns,R); 27 int idxS = expand(j,N/R,R); 28 exchange( v,R,stride, idxD,Ns, idxS,N/R ); 29 } 30 } 31 �
C. Hierarchical FFT
The shared memory FFT is fast but limited in the sizes it
can handle. The hierarchical FFT computes the FFT of a large
sequence by combining FFTs of subsequences that are small
enough to be handled in shared memory. This is analogous to
how the shared memory algorithm computes an FFT of length
N by utilizing multiple FFTs of length R that are performed
entirely in registers. Suppose we have an array A of length
N = NαNβ. We first consider a variation of the standard
“four-step” hierarchical FFT algorithm [23]:
1) Treating A as Nα × Nβ array (row-major), perform Nα
FFTs of size Nβ along the columns.
2) Multiply each element Aij in the array with twiddle
factors ω = e±2πij/N (− for a forward transform, + for
the inverse).
3) Perform N2 FFTs of size Nα along the rows.
4) Transpose A from Nα × Nβ to Nβ × Nα
Nβ is chosen to be small enough that
the FFT can be
performed in shared memory. If Nα is too large to fit into
shared memory, then the algorithm recurses, treating each
row of length Nα as an Nαα × Nαβ array, etc. One way to
think about this algorithm is that it wraps the original one
dimensional array of length N into multiple dimensions, each
small enough that the FFT can be performed in shared memory
along that dimension. The dimensions are then transformed
from highest to lowest. The effect of the multiple transposes
that occur when coming out of the recursion is to reverse the
order of the dimensions, which is analogous to bit-reversal.
The original “four-step” algorithm swaps steps 3 and 4. The
end result is the same, except that FFTs are always performed
along columns. For example, suppose A is partitioned wrapped
into a 3D array with dimensions (N1, N2, N3). The execution
of the original and the modified algorithms can be depicted as
follows:
(N1, N2, N
3)
(N1, N
2, N3)
(N
1, N2, N3)
(N3, N2, N1)
(N1, N2, N
3)
(N3, N1, N
2)
(N3, N2, N
1)
where indicates an FFT transformation along the specified
dimension. The i index in step 2 corresponds an element’s
index in the transformed dimension (Nα) and the j index cor-
responds to the concatenation of the indices in the underlined
dimensions (Nβ). The original algorithm (left) performs all of
the FFTs in-place and uses a series of transposes at the end to
reverse the order of the dimensions. The entire algorithm can
be performed in-place if the transposes are performed in-place.
In-place algorithms can be important for large data sizes. In
the modified algorithm, the FFT computation always takes
place in the current highest dimension and the transposes are
interleaved with the computation. This is analogous to the data
shuffling in a Stockham formulation of a radix-2 FFT used to
avoid bit-reversals.
To reduce the number of passes over the data, we use the
modified algorithm and perform the FFT, the twiddle, and
Fig. 5.
Pseudo-code for shared memory radix-R FFT along columns
used with the hierarchical FFT. strideI and strideO are the strides
of sequence elements on input and output. The kernel
is invoked with
Tx set
to a multiple of R not smaller than CW , Ty = N/R, and
B = (strideI/Tx, M/strideI). The twiddle stage (lines 11–18) and
the transposes (lines 19–27) of the hierarchical algorithm are also included in
the kernel.
greater than CW in length. However, when T > N/R, the
data must first be exchanged between threads. In this case,
the kernel computes more than one FFT at a time and the
number of thread blocks used are reduced accordingly. The
data is then restored to its original order to produce large
contiguous segments when written back to global memory.
When T = N/R, no data exchange is required after reading
from global memory. Because the data is always written back
to the same location from which it was read, the FFT can be
performed in-place. As mentioned previously, bank conflicts
that occur when R is a power of two can be handled with
appropriate padding.
The large number of registers available on NVIDIA GPUs
relative to the size of shared memory can be exploited to
increase performance. Because the data held by each thread
can be stored entirely in registers (in the array v), the FFT
in each iteration (line 26) can be computed without reading
or writing data to memory, and is therefore faster. Shared
memory is used only to exchange data between registers of
different threads. If the number of registers were smaller, then
the data would have to reside primarily in shared memory.
Additional memory might be required for intermediate results.
In particular, the Stockham formulation would require at least
twice the amount of shared memory due to the fact that it is
performed out-of-place. Larger memory requirements reduce
the maximum N that can be handled.
template
void 1 FftShMemCol(int sign, int N, int strideO, 2 float2* dataI, float2* dataO ){ 3 float2 v[R]; 4 int strideI = B.x*T.x; 5 int idxI = (((b.y*N+t.y)*B.x+b.x)*T.x)+t.x; 6 int incI = T.y*strideI; 7 for( int r=0; rthe transpose all in the same kernel. Pseudo-code is shown
in Fig. 5. This version of the FFT assumes that strideI,
the stride between elements in a sequence (the product of the
dimensions preceding the one transformed), is greater than
1 and that product of all the dimensions is a power of R.
The data accesses to global memory for a single FFT along
a dimension greater than 1 are not contiguous. To obtain
contiguous accesses, we transform a block of Mb sequences
at the same time, where Mb is a power of R no smaller than
CW . One side benefit of this is that when R is a power of
two, padding is no longer required to avoid bank conflicts in
exchange() because Mb = CW = 16 is the same as the
number of banks. However, performing such a large number
of FFTs simultaneously means that the N must be partitioned
in dimensions of shorter length due to limits on the number
of registers and the size of shared memory.
Cases where the strides of sequence elements on input and
output, strideI or strideO, are less than Mb require
special handling. When strideI ≥ Mb and strideO
= 1, we rearrange the data in shared memory so that it
can be written out in large contiguous segments (lines 22–
26). strideI can be 1 only if the preceding dimensions
have the trivial length of 1, in which case the FFT can be
computed with FftShMem() from Fig. 4. For all other cases,
specialized code is required to handle the reading and writing
of partial blocks. An alternative is to first transpose the high
dimension to dimension 1, perform the FFT with a variant of
FftShMem() that includes the twiddle from step 2, and then
transpose from dimension 1 to the final destination. However,
these transposes require separate passes over the data and may
sacrifice some performance.
Because global memory FFT algorithm does not involve
global transposes of the data, it can actually be faster than
the hierarchical FFT for large N on GPUs with high memory
bandwidth. We use auto-tuning to determine at which point
to transition from the hierarchical FFT to the global memory
FFT.
D. Mixed-radix FFT
0Rb
So far we have considered algorithms for radix-R algo-
rithms for which N = Ri. To handle mixed-radix lengths
N = Ra
1, the value used for R can be varied in the iterations
of a radix-R algorithm. For example, for N = 2a3b, we can
run a iterations with R = 2 and b iterations with R = 3
using either the global or shared memory FFTs. If 2a and 3b
are small enough to fit in shared memory, but N is too large,
then we can perform the computation hierarchically by setting
Nα = 2a and Nβ = 3b. Specializations of FFT() can be
manually optimized for small primes. When N is a composite
of large primes, we use Bluestein’s FFT.
E. Bluestein’s FFT
The Bluestein’s FFT algorithm computes the DFT of ar-
bitrary length N by expressing it as a convolution of two
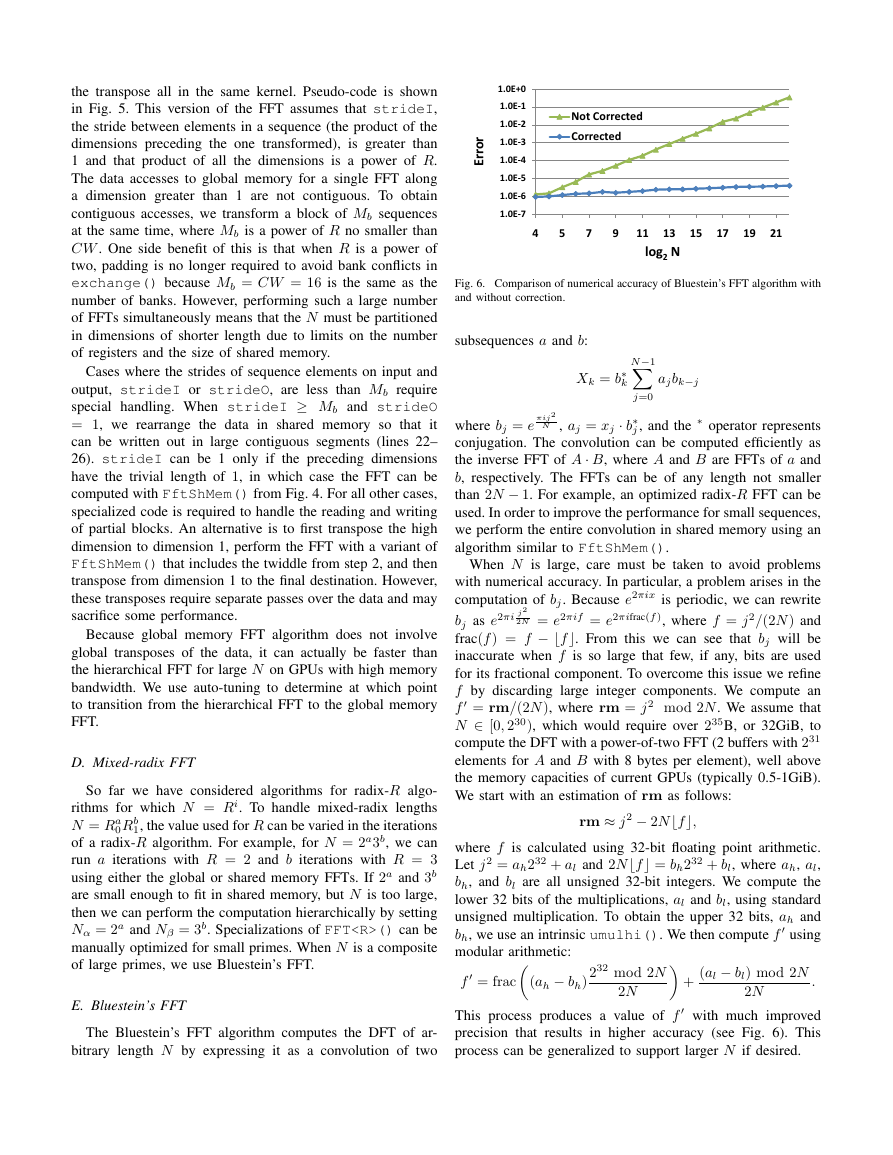
Fig. 6. Comparison of numerical accuracy of Bluestein’s FFT algorithm with
and without correction.
subsequences a and b:
Xk = b∗
k
N−1
j=0
ajbk−j
πij2
N , aj = xj · b∗
j , and the ∗ operator represents
where bj = e
conjugation. The convolution can be computed efficiently as
the inverse FFT of A · B, where A and B are FFTs of a and
b, respectively. The FFTs can be of any length not smaller
than 2N − 1. For example, an optimized radix-R FFT can be
used. In order to improve the performance for small sequences,
we perform the entire convolution in shared memory using an
algorithm similar to FftShMem().
When N is large, care must be taken to avoid problems
with numerical accuracy. In particular, a problem arises in the
computation of bj. Because e2πix is periodic, we can rewrite
bj as e2πi j2
2N = e2πif = e2πifrac(f ), where f = j2/(2N) and
frac(f) = f − f. From this we can see that bj will be
inaccurate when f is so large that few, if any, bits are used
for its fractional component. To overcome this issue we refine
f by discarding large integer components. We compute an
f = rm/(2N), where rm = j2 mod 2N. We assume that
N ∈ [0, 230), which would require over 235B, or 32GiB, to
compute the DFT with a power-of-two FFT (2 buffers with 231
elements for A and B with 8 bytes per element), well above
the memory capacities of current GPUs (typically 0.5-1GiB).
We start with an estimation of rm as follows:
rm ≈ j2 − 2Nf,
where f is calculated using 32-bit floating point arithmetic.
Let j2 = ah232 + al and 2Nf = bh232 + bl, where ah, al,
bh, and bl are all unsigned 32-bit integers. We compute the
lower 32 bits of the multiplications, al and bl, using standard
unsigned multiplication. To obtain the upper 32 bits, ah and
bh, we use an intrinsic umulhi(). We then compute f using
modular arithmetic:
(al − bl) mod 2N
f = frac
.
This process produces a value of f with much improved
precision that results in higher accuracy (see Fig. 6). This
process can be generalized to support larger N if desired.
(ah − bh)
232 mod 2N
+
2N
2N
1.0E-71.0E-61.0E-51.0E-41.0E-31.0E-21.0E-11.0E+04579111315171921Errorlog2NNot CorrectedCorrected�
Fig. 7. GPUs used in experiments. Each multiprocessor can theoretical perform 24 floating point operations (8 FMAD/MUL) per shader clock. The GPUs
use GDDR3 RAM capable of two memory operations per clock. The warp width for all the GPUs is 32. For our performance results we used the driver
versions listed here, unless otherwise specified.
F. Multi-dimensional FFTs
Multi-dimensional FFTs can be implemented by performing
FFTs independently along each dimension. However, perfor-
mance tends to degrade for higher dimensions where the stride
between sequence elements is large. This can sometimes be
overcome by first transposing the data to move the highest
dimension down to the lowest dimension before performing
the FFT. This process can be repeated to cycle through all
the dimensions. By using a kernel like FftShMemCol that
combines the FFT with a transpose, separate transpose passes
over the data can be avoided.
G. Real FFTs and DCTs
FFTs of real sequences have special symmetry. This symme-
try can be used to transform a real FFT into a complex FFT
of half the size. Similarly, trigonmetric transforms, such as
the discrete cosine transform (DCT) can be implemented with
complex FFTs through simple transformation on the data. We
implement real FFTs and DCTs with wrapper functions around
the FFT algorithms that we have presented in this section. We
refer the reader to Van Loan [9] for more details.
V. IMPLEMENTATION
We implemented our FFT library using NVIDIA’s CUDA
API for single-precision data. We have implemented global
memory and shared memory FFT kernels for radices 2, 4, and
8. We use radix-8 for as many iterations as possible. When
N is not divisible by 8, we use radix-2 or radix-4 for the last
iteration. We have also implemented radix-3 and radix-5 for
shared memory.
We use a number of standard optimization techniques that
are not presented in the pseudo-code for the sake of clarity.
The most important optimization is constant propagation. We
use templates to implement specialized kernels for a number
of different sizes and thread counts. Where possible we also
use bit-wise operations to implement integer multiply, divide,
and modulus for power-of-two radices. We also compute some
values common to all threads in a block using a single thread
and store them in shared memory in order to reduce some
computation.
Current GPUs limit the maximum number of threads per
thread block and thread blocks per computation grid. On the
current GPUs, these limits are 512 and 65535 respectively.
These limits restrict the input sizes that can handled. We
overcome these limits by virtualizing. Thread indices are
virtualized by adding loops in the kernels so that a single
thread does the work of multiple virtual threads. Thread blocks
are virtualized by invoking the kernel multiple times and
adding an appropriate offset to the thread block index for
each invocation. Virtualization adds some overhead and code
complexity. Supporting it directly in the runtime would enable
easier programming on GPUs.
When the size of the FFT is too large for shared memory, we
use either the global memory or the hierarchical algorithm. On
all of the GPUs we tested, the performance of the hierarchical
algorithm degrades for larger N while the performance of
the global memory algorithm is nearly constant. At some
point there is a cross-over where the global memory algorithm
becomes faster. We determine the cross over point at runtime
and use the fastest algorithm for a given size.
A. Experimental methodology
VI. RESULTS
We tested our algorithms on three different NVIDIA GPUs:
8800GTX, 8800GTS, and GTX280. The specifications for
these GPUs are summarized in Fig. 7. One of the key
difference between the GPUs is the memory bandwidth. The
GTX280 has the most bandwidth and the 8800GTS has the
least. The GTX280 also has more multiprocessors, which give
it the highest peak performance. We used recent versions
of the drivers. We found, however,
that an older version
of the driver for the GTX280 (177.11) gave significantly
different performance results. Results obtained with this driver
are marked with (∗) in Figs. 11, 12, and 14. We ran our
experiments on a high-end Windows PC equipped with an
Intel QX9650 3.0GHz quad-core processor and 4GB of DDR3
1600 RAM. This processor consists of two dual-core dies in
the same package with each pair of cores sharing a 6 MB L2
cache.
We compared our algorithms to NVIDIA’s CUDA FFT
library (CUFFT) version 1.1 for the GPU and Intel’s Math
Kernel Library (MKL) version 10.2 on the CPU. The MKL
tests utilized four hardware threads and used out-of-place,
single precision transforms. The input and output arrays were
aligned to a multiple of the cache line width. We report
performance in GFlops, which we compute as
D
d=1 Md(5Nd log2 Nd)
execution time
,
where D is the total number of dimensions, Md = E/Nd is
the number of FFTs along each dimension, and E is the total
number of data elements. We follow common convention and
GPU Core Clock (MHz) Shader Clock (MHz) Multi- processors Peak Performance (GFlops) Memory Clock (MHz) Memory (MB) Bus Width (bits) Peak Bandwidth (GiB/s) Driver 8800 GTX 575 1350 16 518 900 768 384 80 175.19 8800 GTS 675 1625 16 624 970 512 256 59 175.19 GTX280 650 1300 30 936 1150 1024 512 137 177.41 �
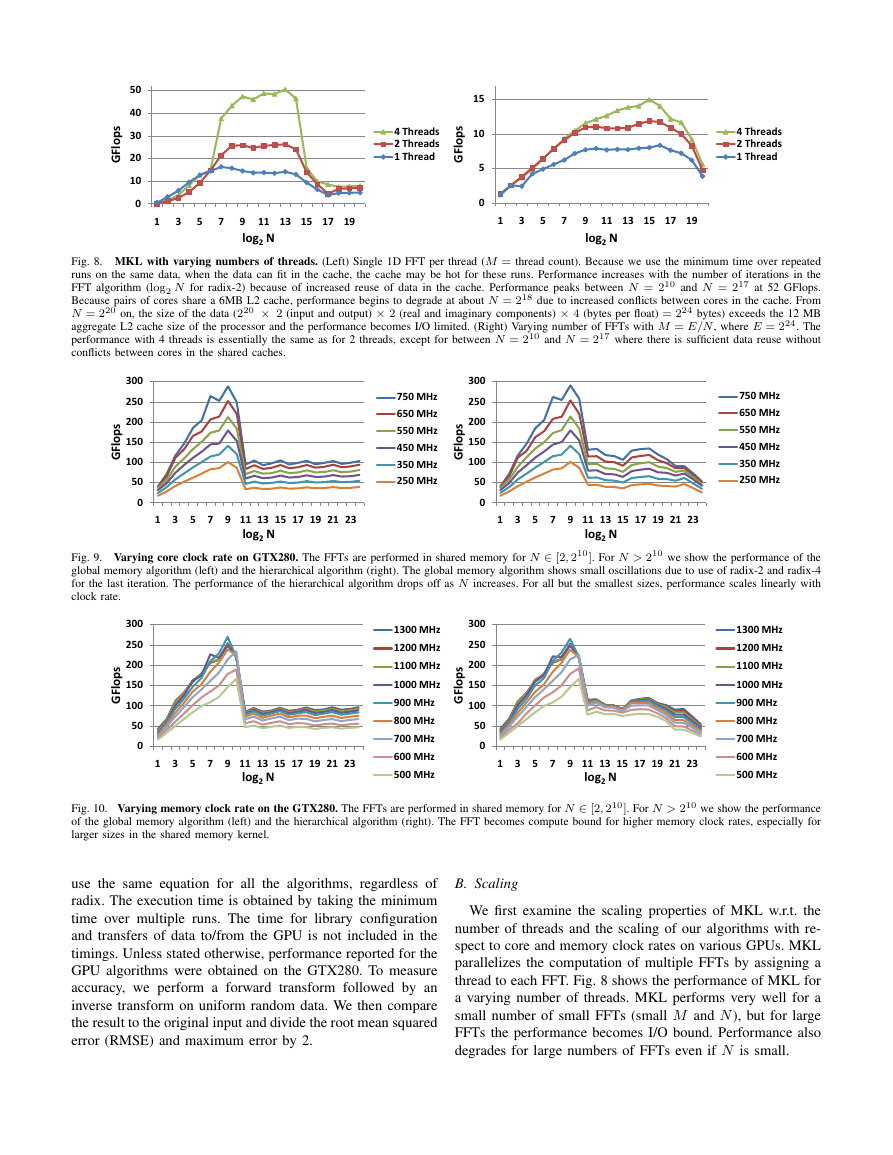
Fig. 8. MKL with varying numbers of threads. (Left) Single 1D FFT per thread (M = thread count). Because we use the minimum time over repeated
runs on the same data, when the data can fit in the cache, the cache may be hot for these runs. Performance increases with the number of iterations in the
FFT algorithm (log2 N for radix-2) because of increased reuse of data in the cache. Performance peaks between N = 210 and N = 217 at 52 GFlops.
Because pairs of cores share a 6MB L2 cache, performance begins to degrade at about N = 218 due to increased conflicts between cores in the cache. From
N = 220 on, the size of the data (220 × 2 (input and output) × 2 (real and imaginary components) × 4 (bytes per float) = 224 bytes) exceeds the 12 MB
aggregate L2 cache size of the processor and the performance becomes I/O limited. (Right) Varying number of FFTs with M = E/N, where E = 224. The
performance with 4 threads is essentially the same as for 2 threads, except for between N = 210 and N = 217 where there is sufficient data reuse without
conflicts between cores in the shared caches.
Fig. 9. Varying core clock rate on GTX280. The FFTs are performed in shared memory for N ∈ [2, 210]. For N > 210 we show the performance of the
global memory algorithm (left) and the hierarchical algorithm (right). The global memory algorithm shows small oscillations due to use of radix-2 and radix-4
for the last iteration. The performance of the hierarchical algorithm drops off as N increases. For all but the smallest sizes, performance scales linearly with
clock rate.
Fig. 10. Varying memory clock rate on the GTX280. The FFTs are performed in shared memory for N ∈ [2, 210]. For N > 210 we show the performance
of the global memory algorithm (left) and the hierarchical algorithm (right). The FFT becomes compute bound for higher memory clock rates, especially for
larger sizes in the shared memory kernel.
use the same equation for all the algorithms, regardless of
radix. The execution time is obtained by taking the minimum
time over multiple runs. The time for library configuration
and transfers of data to/from the GPU is not included in the
timings. Unless stated otherwise, performance reported for the
GPU algorithms were obtained on the GTX280. To measure
accuracy, we perform a forward transform followed by an
inverse transform on uniform random data. We then compare
the result to the original input and divide the root mean squared
error (RMSE) and maximum error by 2.
B. Scaling
We first examine the scaling properties of MKL w.r.t. the
number of threads and the scaling of our algorithms with re-
spect to core and memory clock rates on various GPUs. MKL
parallelizes the computation of multiple FFTs by assigning a
thread to each FFT. Fig. 8 shows the performance of MKL for
a varying number of threads. MKL performs very well for a
small number of small FFTs (small M and N), but for large
FFTs the performance becomes I/O bound. Performance also
degrades for large numbers of FFTs even if N is small.
01020304050135791113151719GFlopslog2N4 Threads2 Threads1 Thread 051015135791113151719GFlopslog2N4 Threads2 Threads1 Thread 0501001502002503001357911131517192123GFlopslog2N750 MHz650 MHz550 MHz450 MHz350 MHz250 MHz 0501001502002503001357911131517192123GFlopslog2N750 MHz650 MHz550 MHz450 MHz350 MHz250 MHz 0501001502002503001357911131517192123GFlopslog2N1300 MHz1200 MHz1100 MHz1000 MHz900 MHz800 MHz700 MHz600 MHz500 MHz 0501001502002503001357911131517192123GFlopslog2N1300 MHz1200 MHz1100 MHz1000 MHz900 MHz800 MHz700 MHz600 MHz500 MHz�














 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc