新型冠状病毒疫情_2020年东三省数学建模A题_论文展示.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：3.29M 资料格式：pdf 举报版权申诉

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第1页.png

第1页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第2页.png

第2页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第3页.png

第3页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第4页.png

第4页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第5页.png

第5页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第6页.png

第6页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第7页.png

第7页 / 共38页

wangpeideeeee-13084333-2020年东三省数学建模A题_论文展示.pdf-第8页.png

第8页 / 共38页

文本预览

新型冠状病毒疫情摘要新型冠状病毒（COVID-2019）目前已经成为世界流行性传染疾病，对各国的经济、人民的生活、生命财产造成了巨大影响。为了弄清新型冠状病毒疫情发展的特点和规律，对于世界范围内的疫情发展能够有一个清晰的认识，我们建立模型,并进行疫情发展趋势的预测。对于问题一,我们收集世界范围内主要国家的新冠疫情数据,通过对四项原始数据的处理,分析确诊人数的增长率和死亡率来确定疫情发展的特点，分析治愈率来确定抗击疫情情况。通过数据挖掘,确立累计确诊人数、新增确诊人数增长率、死亡率、治愈率、每确诊病例医生数、每日新增确诊人数等六项数据处理的指标,采用主成分(PCA)的方法进行降维处理,针对含时间序列的面板数据我们使用峰度统计量计算欧氏距离,最后使用 K-means 对各个国家进行分类。对于问题二,我们确立疫情发展变量和政府干预变量两类。对于疫情发展变量中病死率、治愈率、新增确诊人数增长率、每确诊病例医生数等四项指标,我们通过 PCA 分析确立指标权重,采用 TOPSIS 综合评价得到单个评判函数。对于政府干预变量(9 项指标)所采集的定序型数据,我们建立 CEH 得分函数。综合两类变量, 建立综合评价函数, 我们最终给出主要国家各时间点的管控得分 (stringency index)。对于问题三, 我们建立参数时变的传染动力学 SEIR 模型,对疫情发展进行预测,效果不是很理想,通过模型修正, 基于 LSTM-循环神经网络的时间序列模型, 对主要国家进行每日新增确诊人数能够给出短期的精准预测,通过对照两种预测模型结果,我们给出 LSTM 模型的检验, 在预测的两周时间里最大相对误差为 0.172504。对于问题四,我们通过上述问题的疫情发展和预测,给出合理的建议和展望。关键词：K-means 聚类 PCA 降维 TOPSIS(优劣距离) CEH 得分 LSTM 网络

目录一．问题重述................................................................................................................1 1.1 问题背景.........................................................................................................1 1.2 问题重述.........................................................................................................1 二．问题分析................................................................................................................2 2．1 问题一分析...................................................................................................2 2．2 问题二分析...................................................................................................2 2．3 问题三分析...................................................................................................2 2．4 问题四分析...................................................................................................3 三．模型假设................................................................................................................3 四．符号说明................................................................................................................3 五．建立模型求解........................................................................................................6 5.1 问题一模型的建立与求解.............................................................................6 5.1.1 数学模型的构思...................................................................................6 5.1.2 数据预处理...........................................................................................6 5.1.3 分析疫情的发展特点和疫情抗击效果并进行分类...........................7 5.2 问题二模型的建立与求解...........................................................................10 5.2.1 数学模型的构思.................................................................................10 5.2.2 数据预处理.........................................................................................10 5.2.3 模型建立和求解................................................................................11 5.3 问题三模型建立与求解...............................................................................15 5.3.1 模型的构思.........................................................................................15 5.3.2 模型建立、求解、修正与检验.........................................................15 （1）模型的建立:...............................................................................15 （2）模型的求解:...............................................................................16 （3）模型的修正................................................................................19 （3）模型的检验................................................................................24 5.4 问题四-给世界卫生组织的一封信............................................................. 25 六．模型总结与推广..................................................................................................26 模型总结..............................................................................................................26 模型的优缺点......................................................................................................26 模型的推广..........................................................................................................27 附录..............................................................................................................................28 问题一代码(matlab):......................................................................................... 28 问题三代码_LSTM(python)............................................................................. 30 问题三代码_SEIR(matlab)................................................................................35 参考文献......................................................................................................................36

一．问题重述 1.1 问题背景 2020 年新型冠状病毒爆发，短短几个月内疫情的发展逐渐严峻，严重危害到了广大人民群众的生命和财产安全，引起了社会的广泛关注，各个国家的相关政府部门为应对新型冠状病毒感染的肺炎出台了一系列规范文件，为抗击疫情提供政策法律支持。但病毒依然来势汹汹，疫情消息不断刷新，专家和医护人员每日每夜坚守在岗位上，他们是最美丽的人。本文围绕新型冠状病毒，对各个国家的疫情发展特点进行了分析并对疫情的管控效果进行了综合评价，同时建立了数学模型去预测疫情的发展趋势并提出了建设性意见。 1.2 问题重述新型冠状病毒（COVID-2019）目前已经成为世界流行性传染疾病，对各国的经济、人民的生活、生命财产造成了巨大影响。然而，由于世界上各个国家的经济状况和体制的不同，人们对疫情重视程度的区别，加上很多国家存在的检测设备和个人防护设备的不足，抗击疫情的道路各异，有些国家已经看到了曙光，有的国家还有很长的路要走。弄清新型冠状病毒疫情发展的特点和规律，对于世界范围内的疫情发展能够有一个清晰的认识，我们团队需要搜集数据，建立数学模型，解决如下问题: 问题 1.根据与疫情发展相关的时间序列数据，分析世界范围内主要国家的疫情发展的特点及抗击疫情状况，并进行合理的分类。问题 2.选取合理的指标，构建数学模型，对世界范围主要国家对疫情的管控效果进行综合评价。问题 3.分别建立模型对世界范围内主要国家的疫情发展趋势进行预测，需要对模型进行检验。问题 4.根据你们的研究，给世界卫生组织写一封信，提出一些有针对性的抗击疫情的建议和对未来疫情发展的展望。 1

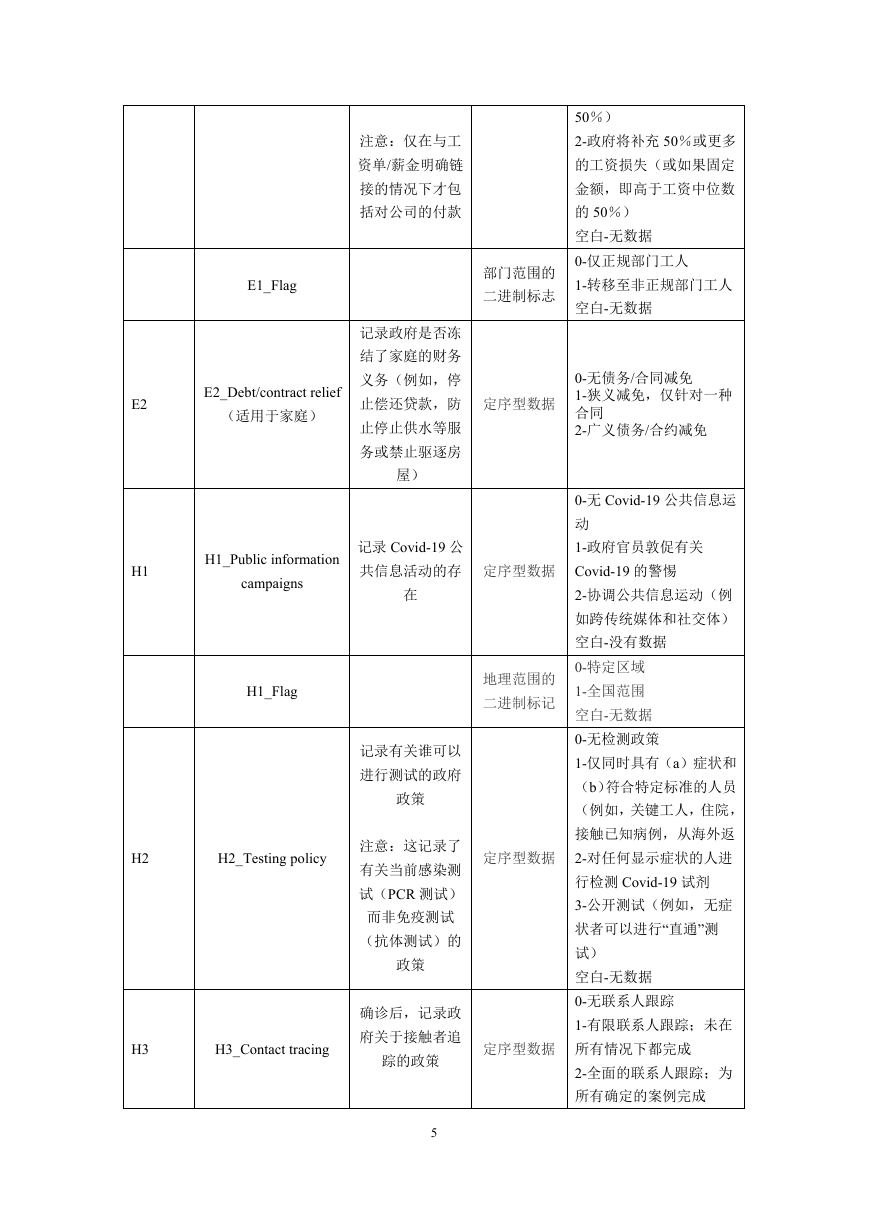
二．问题分析 2．1 问题一分析问题一需要收集与疫情有关的时间序列数据,确立指标对世界范围内主要国家进行疫情特点分析(例如, 死亡率来确定疫情发展的特点，通过分析治愈率来确定抗击疫情情况),同时需要将多个案多指标(6 项指标)的面板数据进行降维处理, 提取合适的单一特征量(可以是峰度、偏度、均值、标准差等),作为 K-means 算法的输入,进而将主要国家进行分类。采用美国约翰斯·霍普金斯大学全球新冠疫情统计数据集[1]和世界卫生组织官网[2]医生数据,收集世界范围内主要国家的新冠疫情累计确诊人数、累计死亡人数、累计治愈人数和每万人医生数等四项原始指标。 2．2 问题二分析问题二，需要我们选取合理指标,构建综合评价模型。我们确立疫情发展变量和政府干预变量两类。其中疫情发展变量包括病死率、治愈率、新增确诊人数增长率、每确诊病例医生数等四项指标。政府干预变量包括政府政策(C1..C4)、经济政策(E1..E2)和卫生系统政策(H1..H3)等共 9 项指标。采用牛津大学新冠疫情政府响应追踪系统的数据集。指标确立以后,我们将建立综合评价模型,针对疫情发展变量,通过客观定权的主成分法,确立权重,再进行 TOPSIS 综合评价得到单个评判函数。针对政府干预变量,我们确立 CEH 得分函数。将两个评判函数算术平均,得到我们最终的综合评价函数,进而给出各个国家的时间步上的管控得分(stringency index)。 2．3 问题三分析问题三,需要我们预测疫情发展趋势,根据时间序列的数据,我们建立传统的参数时变的 SEIR 模型,给出仿真结果,观察其效果。通过模型修正,我们建立深度学习理论中的 LSTM(循环神经网络)模型,对主要国家每日新增确诊人数做出预测,对照两种模型,给出其相似度检验。 2

2．4 问题四分析根据前三问的世界范围内主要国家的分类、综合评价以及预测,我们写信,提出合理的建议和展望。三．模型假设 1．假设选取时间不变。 2．假设累计统计数据时间为晚上 10 点至 12 点 3．假设取相同时间段的增长率，死亡率等数据峰值统计量作为该国家的增长率，      死亡率等数据的特征值。 4．假设每确诊病例的医生数取以现存每十万人确诊数除以每十万人的医生数， 5 ．假设总人数 N 不变，分为易感者 S, 潜伏者 E, 感染者 I, 治愈者 , 为感染系数， k 为转化率，治愈率，为病死率。 R N S E I R D 感染系数为患者平均每天可以感染的易感者的数量，是流行病传染模型中的重要参数。感染系数＝感染者每天平均接触人数×接触感染者后易感者患病的概率。 6．由于各国 Cov-19 的患者数量占人群总数的比例较小，因此本研究假设易感人数始终等于人群总数，即 S＝N。四．符号说明符号 1R 2R 3R 4R mA  k  μ 定义病死率指标治愈率指标新增确诊人数增长率指标每确诊病例医生数单个国家的 m 个时间节点感染系数转化率治愈率死亡率 3

Name Description Measurement Coding ID C1 C2 C1_School closing 记录学校和大学定序型数据学校关闭的关闭时间 C1_Flag 地理范围的二进制标记 C2_Workplace closing 记录工作场所的工作场所关闭关闭定序型数据 0-无措施 1-建议关闭 2-要求关闭（仅某些级别例如，仅高中或公立学校） 3-要关闭所有级别空白-无数据 0-特定区域 1-全国范围空白-无数据 0-无措施 1-建议关闭(或建议在工作) 2-要求关闭（或在家工作）某些部门或类别的工人 3-要求关闭（或在家工作）所有基本工作场所（例如杂货店，医生）空白-无数据 0-特定区域 1-全国范围空白-无数据 0-无措施 1-建议取消 2-要求取消空白-无数据 0-特定区域 1-全国范围空白-无数据 0-禁止采取任何措施 1-建议关闭（或大幅度减少可用的运输量/路线/运输方式） 2-要求关闭（或禁止大多数公民使用） 0-特定区域 1-全国范围空白-无数据 0-没有收入支持 1-政府将补偿少于工资损失的 50％（或者固定金额，低于中位数工资的 C2_Flag 地理范围的二进制标记 C3 C3_Cancel public 记录取消的公共定序型数据 events 活动 C3_Flag 地理范围的二进制标记 C4_Close public 记录公共交通关 C4 transport 闭定序型数据 C4_Flag E1 E1_Income support （适用于家庭）地理范围的二进制标记定序型数据记录政府是否向失业或无法工作的人提供直接现金支付。 4

注意：仅在与工资单/薪金明确链接的情况下才包括对公司的付款 E1_Flag 部门范围的二进制标志 E2_Debt/contract relief （适用于家庭）记录政府是否冻结了家庭的财务义务（例如，停止偿还贷款，防定序型数据止停止供水等服务或禁止驱逐房屋） H1_Public information campaigns 记录 Covid-19 公共信息活动的存在定序型数据 E2 H1 H1_Flag 地理范围的二进制标记 H2 H2_Testing policy H3 H3_Contact tracing 记录有关谁可以进行测试的政府政策注意：这记录了有关当前感染测试（PCR 测试）而非免疫测试（抗体测试）的政策确诊后，记录政府关于接触者追踪的政策 5 定序型数据定序型数据 50％） 2-政府将补充 50％或更多的工资损失（或如果固定金额，即高于工资中位数的 50％）空白-无数据 0-仅正规部门工人 1-转移至非正规部门工人空白-无数据 0-无债务/合同减免 1-狭义减免，仅针对一种合同 2-广义债务/合约减免 0-无 Covid-19 公共信息运动 1-政府官员敦促有关 Covid-19 的警惕 2-协调公共信息运动（例如跨传统媒体和社交体）空白-没有数据 0-特定区域 1-全国范围空白-无数据 0-无检测政策 1-仅同时具有（a）症状和（b）符合特定标准的人员（例如，关键工人，住院，接触已知病例，从海外返 2-对任何显示症状的人进行检测 Covid-19 试剂 3-公开测试（例如，无症状者可以进行“直通”测试）空白-无数据 0-无联系人跟踪 1-有限联系人跟踪；未在所有情况下都完成 2-全面的联系人跟踪；为所有确定的案例完成

五．建立模型求解 5.1 问题一模型的建立与求解 5.1.1 数学模型的构思针对各个国家在相同的时间段内,我们通过各个国家的累计确诊人数，累计死亡人数，累计治愈人数,每万人医生数等四项原始指标,来确立确诊人数增长率，死亡率，治愈率分析了各个国家疫情的发展特点。通过对收集的面板数据的处理和挖掘,建立多指标(6 项指标:累计确诊人数、新增确诊人数增长率、死亡率、治愈率、每确诊病例医生数(取以 10 为底的对数)、每日新增确诊人数等), 采用主成分(PCA)的方法进行降维处理, 针对含时间序列的面板数据我们使用峰度统计量计算欧氏距离,然后使用基于距离的聚类算法 K-means 将各个国家进行分类。 5.1.2 数据预处理 (1) 计算时所需要公式新增确诊人数增长率=新增人数/累计确诊人数死亡率=累计死亡人数/累计确诊人数治愈率=累计治愈人数/累计确诊人数每确诊病例医生数=累计确诊人数/每万人医生数*10000 每日新增确诊人数=当天累计确诊人数-昨天累计确诊人数 (2) 数据说明通过找到的相关面板数据,对指标进行峰值求解,将峰值统计量作为待处理数据，然后对待处理数据进行标准化处理，通过主成分降维处理找到最贴近的数据，通过主成分分析，发现所研究指标中前三个累计贡献率超过 80%,说明前三个主成分基本包含了全部指标具有的信息，前三个主成分是累计确诊人数，新增确诊人数增长率，死亡率。 6

分享到：

赞收藏

资料库

新型冠状病毒疫情_2020年东三省数学建模A题_论文展示.pdf

相关推荐

人工智能

热门标签

最新资料