信 息 技 术 2008 NO.29 SCIENCE & TECHNOLOGY INFORMATION 科技资讯 基于 F P G A 的数字积分器设计 ( 燕山大学图书馆 秦皇岛 0 6 6 0 0 4 ) 曾 涛 摘 要: 在通信系统和传感器系统的设计中, 数字积分器是重要环节。本文提出基于 F P G A 来实现数字积分器的方法, 其受环境干扰小, 可靠性和可重复性高, 设计灵活, 方法简单易行。 关键词: 数字积分器 FPGA 采样频率 中图分类号:TN722 文献标识码:A 文章编号:1672-3791(2008)10(b)-0017-01 1 积分算法选择 积 分 算 法 的 选 择 应 该 遵 循 以 下 原 则 : 低的采样频率要求和简单的结构。一般来 说, 用 数 字 方 式 实 现 的 积 分 器 进 行 运 算 的 样点越多, 积分效果越好, 误差越小, 但运 算时间越长。在实用中要综合考虑速度和 精度等因素, 选择合适的样点数[ 1 ] 。 复化的矩形公式、梯形公式和 Simpson 公 式 都 是 常 用 的 数 字 积 分 算 法 。它 们 的 Z 传递函数 H R 、H T 和 H S 分别为[ 2 ～3 ] : (1) 其中 f 为模拟频率; fs 为采样频率; N 为 单位周期内采样点数。这样就可以计算某种 算 法 在 某 种 精 度 要 求 下 所 必 需 的 最 小 N 。 结 合 前 面 的 分 析 可 知 , 相 同 的 精 度 要 求下, 矩形公式为满足相角误差要求, 一般 所需的采样点数 N 较大, 这就导致了采样 率 一 定 的 情 况 下, 满 足 近 似 积 分 关 系 的 带 宽变窄; 梯形公式所需的 N 适中; S i m p s o n 公式所需的 N 最少。 从 结 构 复 杂 程 度 分 析 , 矩 形 公 式 的 结 构最简单, 梯形公式次之, S i m p s o n 公式的 结 构 最 复 杂 。 综 合 比 较 各 项 指 标 , 选 择 梯 形 公 式 做 (2) 为 数 字 积 分 的 算 法 。 2 积分器的数字化 满 足 梯 形 公 式 的 离 散 差 分 方 程 为 : y[n]=y[n-1]+1/2(x[n]+x[n-1]) (11) 由 此 差 分 方 程 可 知 , 梯 形 积 分 器 相 当 于一个一阶 I I R (无限脉冲响应) 滤波器。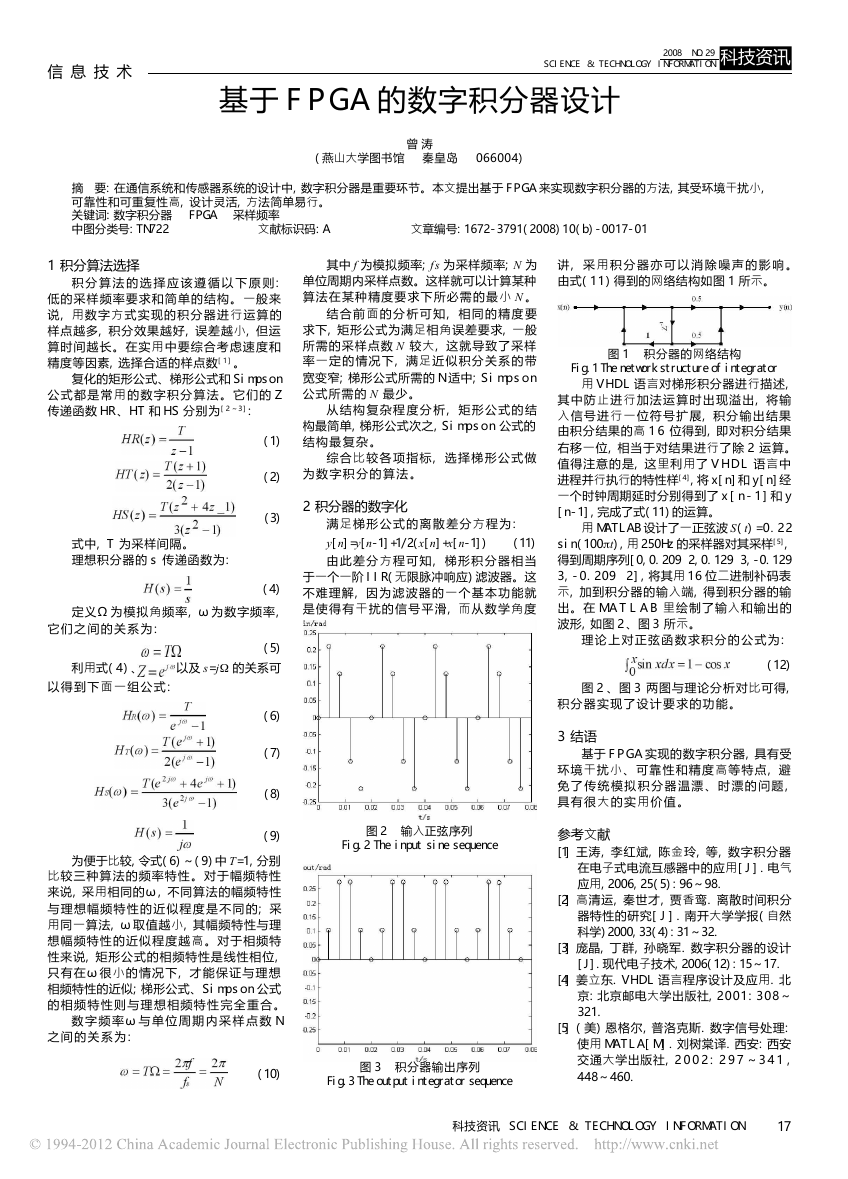这 不难理解, 因 为 滤 波 器 的 一 个 基 本 功 能 就 是 使 得 有 干 扰 的 信 号 平 滑, 而 从 数 学 角 度 图 2 输入正弦序列 Fig.2 The input sine sequence (3) 式中, T 为采样间隔。 理想积分器的 s 传递函数为: (4) 定义Ω为模拟角频率, ω为数字频率, 它 们 之 间 的 关 系 为 : 利用式( 4 ) 、 (5) 以及 s= jW 的关系可 以 得 到 下 面 一 组 公 式 : (6) (7) (8) (9) 为便于比较,令式(6)～(9)中 T=1,分别 比较三种算法的频率特性。对于幅频特性 来说, 采用相同的ω, 不同算法的幅频特性 与 理 想 幅 频 特 性 的 近 似 程 度 是 不 同 的; 采 用同一算法, ω取值越小, 其幅频特性与理 想幅频特性的近似程度越高。对于相频特 性来说, 矩形公式的相频特性是线性相位, 只 有 在ω很 小 的 情 况 下 , 才 能 保 证 与 理 想 相频特性的近似; 梯形公式、S i m p s o n 公式 的 相 频 特 性 则 与 理 想 相 频 特 性 完 全 重 合 。 数 字 频 率 ω 与 单 位 周 期 内 采 样 点 数 N 之 间 的 关 系 为 : 讲 , 采 用 积 分 器 亦 可 以 消 除 噪 声 的 影 响 。 由式( 1 1 ) 得到的网络结构如图 1 所示。 图 1 积分器的网络结构 Fig.1 The network structure of integrator 用 V H D L 语言对梯形积分器进行描述, 其 中 防 止 进 行 加 法 运 算 时 出 现 溢 出, 将输 入 信 号 进 行 一 位 符 号 扩 展, 积 分 输 出 结 果 由积分结果的高 1 6 位得到, 即对积分结果 右移一位, 相当于对结果进行了除 2 运算。 值得注意的是, 这里利用了 V H D L 语言中 进程并行执行的特性样[4],将 x[n]和 y[n]经 一个时钟周期延时分别得到了 x [ n - 1 ] 和 y [n-1],完成了式(11)的运算。 用 M A T L A B 设计了一正弦波 S( t) = 0 . 2 2 sin(100pt),用 250Hz 的采样器对其采样[5], 得到周期序列[0,0.209 2,0.129 3,-0.129 3 , - 0 . 2 0 9 2 ] , 将其用 1 6 位二进制补码表 示, 加到积分器的输入端, 得到积分器的输 出。在 M A T L A B 里绘制了输入和输出的 波形, 如图 2 、图 3 所示。 理 论 上 对 正 弦 函 数 求 积 分 的 公 式 为 : (12) 图 2 、图 3 两图与理论分析对比可得, 积 分 器 实 现 了 设 计 要 求 的 功 能 。 3 结语 基于 F P G A 实现的数字积分器, 具有受 环 境 干 扰 小 、 可 靠 性 和 精 度 高 等 特 点 , 避 免 了 传 统 模 拟 积 分 器 温 漂 、 时 漂 的 问 题 , 具 有 很 大 的 实 用 价 值 。 参考文献 [1] 王涛, 李红斌, 陈金玲, 等, 数字积分器 在电子式电流互感器中的应用[ J ] . 电气 应用,2006,25(5):96～98. [2] 高清运, 秦世才, 贾香鸾. 离散时间积分 器特性的研究[ J ] . 南开大学学报( 自然 科学)2000,33(4):31～32. [3] 庞晶, 丁群, 孙晓军. 数字积分器的设计 [J].现代电子技术,2006(12):15～17. [4] 姜立东. V H D L 语言程序设计及应用. 北 京: 北京邮电大学出版社, 2 0 0 1 : 3 0 8 ～ 321. [5] ( 美) 恩格尔, 普洛克斯. 数字信号处理: 使用 M A T L A [ M ] . 刘树棠译. 西安: 西安 交通大学出版社, 2 0 0 2 : 2 9 7 ～3 4 1 ， 448～460. (10) 图 3 积分器输出序列 Fig.3 The output integrator sequence 科技资讯 S C I E N C E & T E C H N O L O G Y I N F O R M A T I O N 17