第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
论文研究 - 基于JND模型的感知视频编码.pdf
A Perceptual Video Coding Based on JND Model
Abstract
Keywords
1. Introduction
2. Nonlinear Additively Masking Model
3. Improved JND Model Based on DCT Domain
3.1. Spatial-Temporal Contrast Sensitivity Function
3.2. Luminance Adaptive Factor and Contrast Masking Factor
4. Simulation Results
4.1. Evaluation of the Improved JND Model Based on Transform Domain
4.2. The Overall Performance of the Perceptual Video Coding Scheme
Acknowledgements
References
Journal of Computer and Communications, 2018, 6, 53-64
http://www.scirp.org/journal/jcc
ISSN Online: 2327-5227
ISSN Print: 2327-5219
A Perceptual Video Coding Based on JND Model
Qingming Yi, Wenhui Fan, Min Shi
College of Information Science and Technology, Jinan University, Guangdong, China
How to cite this paper: Yi, Q.M., Fan,
W.H. and Shi, M. (2018) A Perceptual
Video Coding Based on JND Model. Jour-
nal of Computer and Communications, 6,
53-64.
https://doi.org/10.4236/jcc.2018.64005
Received: March 27, 2018
Accepted: April 23, 2018
Published: April 26, 2018
Copyright © 2018 by authors and
Scientific Research Publishing Inc.
This work is licensed under the Creative
Commons Attribution International
License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/
Open Access
Abstract
In view of the fact that the current high efficiency video coding standard does
not consider the characteristics of human vision, this paper proposes a per-
ceptual video coding algorithm based on the just noticeable distortion model
(JND). The adjusted JND model is combined into the transformation quanti-
zation process in high efficiency video coding (HEVC) to remove more visual
redundancy and maintain compatibility. First of all, we design the JND model
based on pixel domain and transform domain respectively, and the pixel do-
main model can give the JND threshold more intuitively on the pixel. The
transform domain model introduces the contrast sensitive function into the
model, making the threshold estimation more precise. Secondly, the proposed
JND model is embedded in the HEVC video coding framework. For the
transformation skip mode (TSM) in HEVC, we adopt the existing pixel do-
main called nonlinear additively model (NAMM). For the non-transformation
skip mode (non-TSM) in HEVC, we use transform domain JND model to
further reduce visual redundancy. The simulation results show that in the case
of the same visual subjective quality, the algorithm can save more bitrates.
Keywords
High Efficiency Video Coding, Just Noticeable Distortion, Nonlinear
Additively Model, Contrast Sensitivity Function
1. Introduction
Nowadays, high definition video is becoming more and more popular. However,
the growth of storage capacity and network bandwidth cannot meet the de-
mands for high resolution for storage and transmission. Therefore, ITU-T and
ISO/IEC worked together to release a new generation of efficient video coding
standard—HEVC [1]. HEVC still follows the traditional hybrid coding frame-
work and uses statistical correlation to remove space and time redundancy in
order to achieve the highest possible compression effect. However, as the ulti-
DOI: 10.4236/jcc.2018.64005 Apr. 26, 2018
53
Journal of Computer and Communications
Q. M. Yi et al.
mate receiver of video, Human Visual System [2] has some visual redundancy
due to its own characteristics. In order to get the perceptual redundancy, re-
searchers have done a lot of work, of which the widely accepted model is the just
noticeable distortion model. Video encoding based on perceptible distortion is
mainly to use the human eye’s visual masking mechanism. When the distortion
is less than the human sensitivity threshold, the human eye is imperceptible [3].
In recent years, the JND model has received wide attention in the aspects of
video image encoding [4] [5], digital watermarking [6], image quality evaluation
[7] and so on. At present, several JND models have been proposed: the JND
model based on pixel domain and the JND model based on transform domain.
For the JND model based on pixel domain, it usually considers two main fac-
tors including luminance adaptive masking and contrast masking effect. C. H.
Chou and Y. C. Li [8] proposed the pixel domain JND model for the first time.
The lager one of the calculated luminance adaptive masking value and contrast
masking effect value was used as the final JND threshold. Yang [9] and others
proposed the classical nonlinear additively masking model. The two kinds of
masking effects were added together to get the corresponding JND values. To
some extent, the interaction between the two masking effects was considered. To
solve the problem of lack of precision in the calculation of the contrast masking
value for the above methods, Liu [10] assigned different weights to texture re-
gion and edge region in the image through texture decomposition on the basis of
NAMM model, which made the JND model have better calculation accuracy.
Wu [11] proposed a JND model based on luminance adaptive and structural si-
milarity, which further considered the sensitivity of human eyes to different reg-
ular and irregular regions when computing texture masking.
The JND model based on transform domain could easily introduce the con-
trast sensitivity function into the model with high accuracy. Since most image
coding standards adopt DCT transform, the JND model based on DCT domain
has attracted much attention of researchers. Ahumada et al. [12] obtained a JND
model of a grayscale image by calculating the spatial CSF function. Based on
this, Waston [13] proposed the DCTune method, further considering the fea-
tures of luminance adaptation and contrast masking. Zhang [14] made the JND
model more accurate by adding a luminance adaptive factor and a contrast
masking factor. Wei et al. [15] introduced gamma correction to the JND model
and proposed a more accurate video image JND model.
2. Nonlinear Additively Masking Model
The NAMM model is simulated in pixel domain from the aspects of luminance
adaptation and texture masking to obtain the JND threshold of pixel domain.
The JND estimation based on the pixel domain can be written as the nonlinear
additively of the luminance adaptation and the contrast masking, as shown in
Equation (1):
JND
pixel
(
x y
,
)
=
l
T x y
,
(
)
+
t
T x y C
−
,
lt
⋅
min
(
)
{
T x y T x y
,
(
)
(
,
,
l
t
}
)
(1)
DOI: 10.4236/jcc.2018.64005
54
Journal of Computer and Communications
Q. M. Yi et al.
(
)
(
)
,
,
lT x y and
tT x y denote the basic threshold of adaptive back-
where,
ground luminance and texture masking; Clt represents the overlapping part of
two kinds of effects, and it is used to adjust the two factors. The larger the Clt
value is, the stronger superposition between the adaptive background luminance
and texture masking is. When Clt is 1, the superposition effect between the two
factors is the greatest; when Clt is 0, there is no superposition effect between the
two effects. In fact, the superposition is between the maximum and the mini-
mum, where Clt is equal to 0.3.
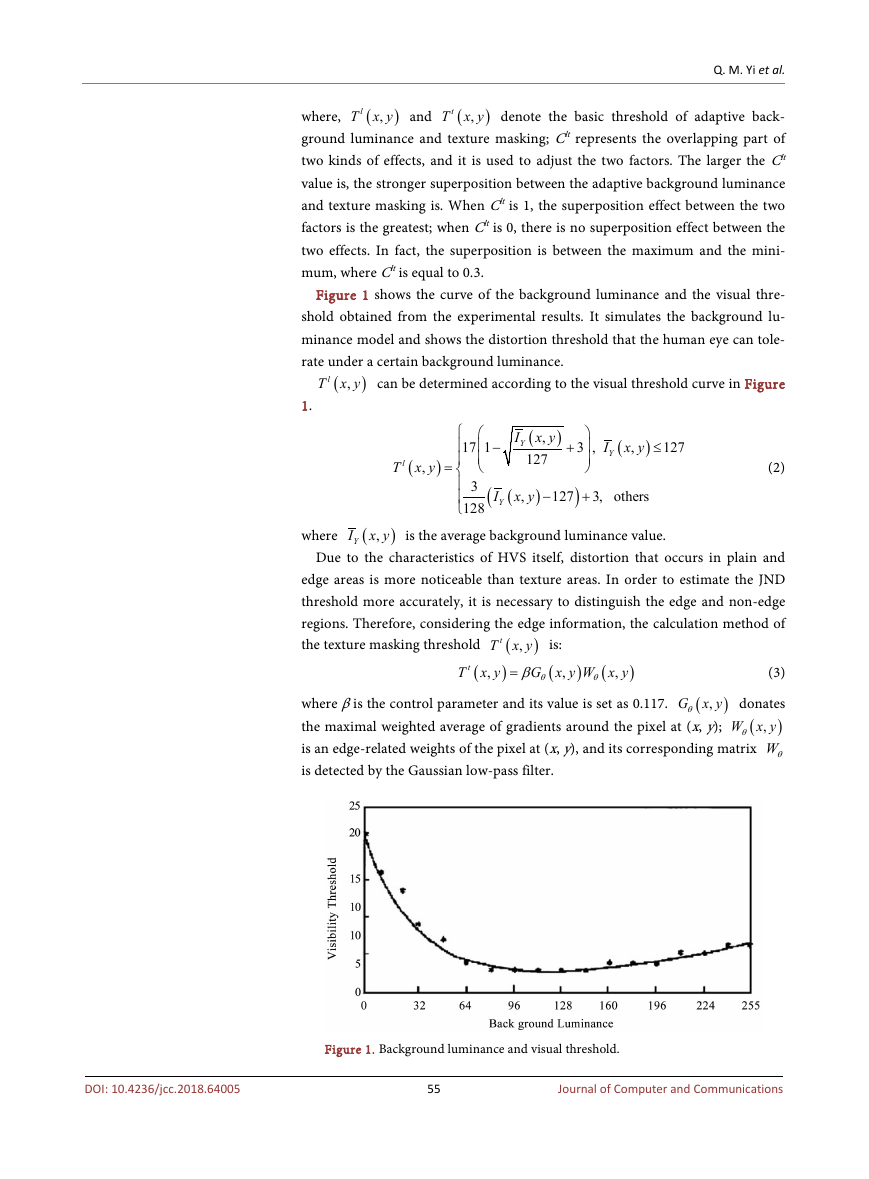
Figure 1 shows the curve of the background luminance and the visual thre-
shold obtained from the experimental results. It simulates the background lu-
minance model and shows the distortion threshold that the human eye can tole-
rate under a certain background luminance.
lT x y can be determined according to the visual threshold curve in Figure
,
(
)
1.
l
T x y
,
(
)
17 1
=
3
128
(
−
I
Y
)
(
x y
,
127
+
3 ,
I
Y
(
x y
,
)
≤
127
I
Y
(
x y
,
)
−
127
)
+
3, others
(2)
where
YI
(
x y is the average background luminance value.
,
)
Due to the characteristics of HVS itself, distortion that occurs in plain and
edge areas is more noticeable than texture areas. In order to estimate the JND
threshold more accurately, it is necessary to distinguish the edge and non-edge
regions. Therefore, considering the edge information, the calculation method of
the texture masking threshold
(
tT x y is:
x y
x y W
,
,
θ
(3)
)
(
,
)
G
β=
θ
x y
,
tT
(
)
(
)
)
,G x y
donates
where β is the control parameter and its value is set as 0.117.
θ
)
,W x y
the maximal weighted average of gradients around the pixel at (x, y);
is an edge-related weights of the pixel at (x, y), and its corresponding matrix Wθ
is detected by the Gaussian low-pass filter.
(
(
θ
DOI: 10.4236/jcc.2018.64005
Figure 1. Background luminance and visual threshold.
55
Journal of Computer and Communications
Q. M. Yi et al.
,G x y
θ
(
)
with
is defined as:
(
G x y
θ
,
)
=
max
k
1,2,3,4
=
{
grad
,
θ
k
(
x y
,
}
)
(4)
grad
,
θ
k
(
x
,
y
)
=
1
16
5
5
∑∑
i
1
=
1
=
j
I
θ
(
x
− +
3
i
,
y
− +
3
)
j
×
(
g i
k
,
)
j
(5)
(
kg i
where,
shown in Figure 2.
)
j
,
are four directional high-pass filters for texture detection, as
3. Improved JND Model Based on DCT Domain
A typical JND model based on DCT domain is expressed as a product of a base
threshold and some modulation factors. Assume that t is expressed as the frame
index in the video sequence, n is the block index in the tth frame, and (i, j) is the
DCT coefficient index. Then the corresponding JND threshold can be expressed
as:
JND
DCT
(
n i
, ,
j t
,
)
=
(
T n i
, ,
j t
,
)
×
a
Lum
(
n t
,
)
×
a
Contrast
(
n i
, ,
j t
,
)
(6)
(
T n i
, ,
)
j t
,
where
calculated from the spatial-temporal contrast sensitivity function;
denotes the luminance adaptation factor;
trast masking factor.
is the spatial-temporal base distortion threshold, which is
)
n t
,
is expressed as a con-
a
Contrast
a
Lum
n i
, ,
j t
,
(
(
)
3.1. Spatial-Temporal Contrast Sensitivity Function
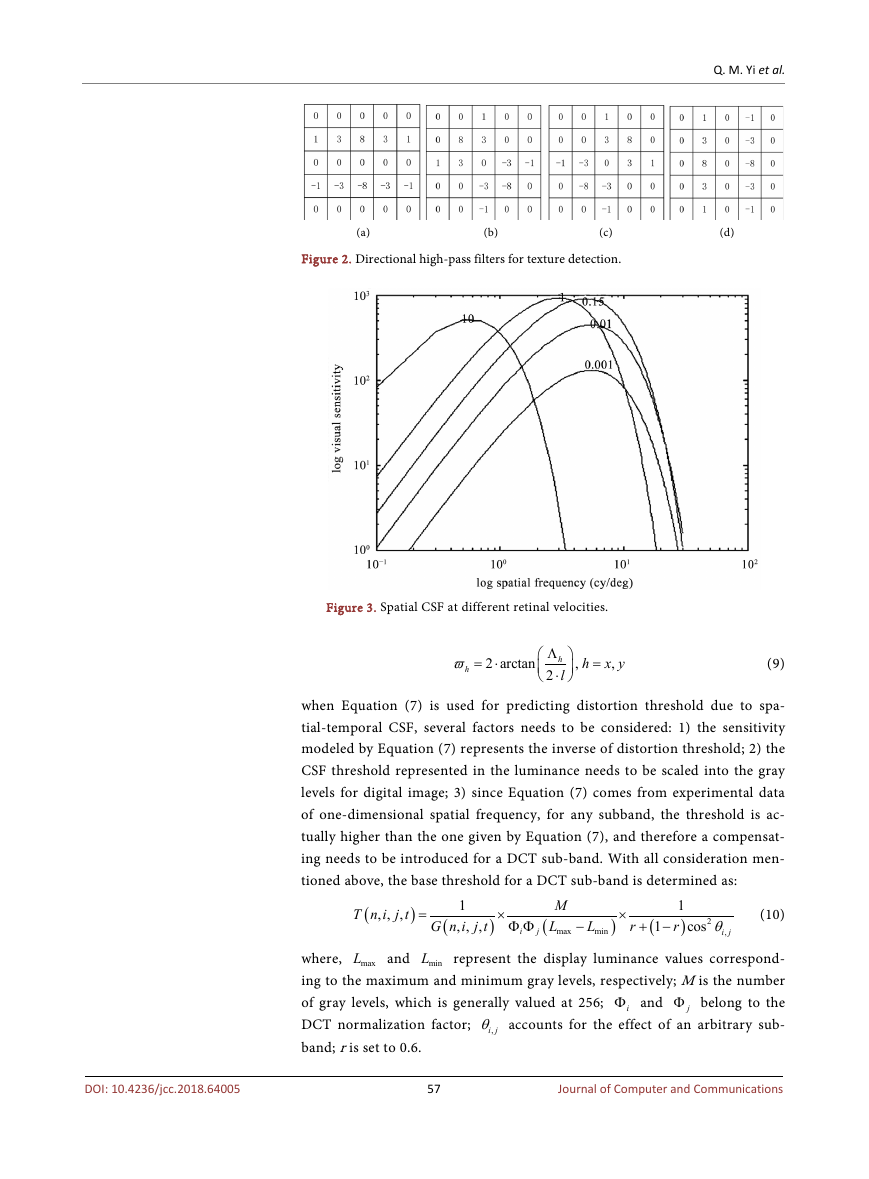
In psychophysics experiments, the visual sensitivity of the human eye is re-
lated to the spatial frequency and time frequency of the input signal. The
contrast sensitive function is usually used to quantify the relationship be-
tween these factors. It is defined as the inverse of the distortion perceived by
human eye, when the contrast changes. The spatial-temporal contrast sensi-
tivity function curve is shown in Figure 3. If we consider the (i, j) th in the
nth DCT block in the tth frame, then the corresponding CSF function can be
written as:
⋅
(
(
)
n t
,
εν
(
(
c
⋅
εν
1
⋅
⋅
3
)
)
n t
,
+
3
)
) (
⋅
2π
ρ
i j
.
2
)
(7)
(
ν
⋅
)
2
n t
,
)
3
k
G n i
, ,
(
j t
,
)
=
c
0
k
1
+
k
2
log
(
⋅
exp
(
2π
−
ρ
i j
.
(
),n tν
1k ,
where
constant
magnitude and the bandwidth of a CSF curve;
frequency:
depicts the associated retinal image velocity; the empirical
1c control the
2k and
.i jρ is the spatial subband
3k are set as 6.1, 7.3 and 23.
0c and
ρ
i j
.
=
1
N
2
(
i
ϖ
x
2
)
+
(
j
ϖ
y
)2
(8)
xϖ and
yϖ are the horizontal and vertical sizes of a pixel in degrees
where,
of visual angle, respectively. They are related to the viewing distance l and the
display width Λ of a pixel on the monitor, as follows:
56
Journal of Computer and Communications
DOI: 10.4236/jcc.2018.64005
Q. M. Yi et al.
(a) (b) (c) (d)
Figure 2. Directional high-pass filters for texture detection.
Figure 3. Spatial CSF at different retinal velocities.
ϖ
h
= ⋅
2 arctan
Λ
2
h
⋅
l
,
h
=
x y
,
(9)
when Equation (7) is used for predicting distortion threshold due to spa-
tial-temporal CSF, several factors needs to be considered: 1) the sensitivity
modeled by Equation (7) represents the inverse of distortion threshold; 2) the
CSF threshold represented in the luminance needs to be scaled into the gray
levels for digital image; 3) since Equation (7) comes from experimental data
of one-dimensional spatial frequency, for any subband, the threshold is ac-
tually higher than the one given by Equation (7), and therefore a compensat-
ing needs to be introduced for a DCT sub-band. With all consideration men-
tioned above, the base threshold for a DCT sub-band is determined as:
(
T n i
, ,
j t
,
)
=
1
G n i
, ,
(
×
j t
,
)
M
L
max
(
Φ Φ
i
j
×
−
L
min
)
r
(
1
+ −
1
)
r
2
cos
θ
i j
,
(10)
maxL
and
minL
where,
represent the display luminance values correspond-
ing to the maximum and minimum gray levels, respectively; M is the number
of gray levels, which is generally valued at 256;
jΦ belong to the
DCT normalization factor;
,i jθ accounts for the effect of an arbitrary sub-
band; r is set to 0.6.
iΦ and
DOI: 10.4236/jcc.2018.64005
57
Journal of Computer and Communications
Q. M. Yi et al.
3.2. Luminance Adaptive Factor and Contrast Masking Factor
The luminance masking mechanism is related to the brightness change in the
image. According to Weber-Fechner’s law, the minimum perceptible luminance
of human eye shows a higher threshold in the areas with brighter or darker
background brightness, which is called luminance adaptive effect. The calcula-
tion formula of the luminance adaptive factor is:
+
150 1,
170
+
)
I
I
)
170 425 1,
(11)
(
−
60
=
1, 60
(
I
−
a
Lum
170
n t
,
60
≤
≥
(
)
I
I
where I represents the average brightness.
The contrast masking effect is an important perceptual property in the HVS,
usually related to the awareness of a signal in the presence of another signal.
When the contrast sensitivity factor is calculated, the image is first detected by
Canny edge, and the image blocks are divided into three types: plain, edge and
texture region. Since the human eye is more sensitive to distortions that occur in
plain areas and in edge areas, different weights need to be assigned to different
areas. Based on the above considerations, the weighted factor for each classifica-
tion block is determined by the following equation:
ψ
1,in plain and edge region
=
2.25,
nd
1.
in texture region a
in texture regi
25
,
an
on
d
2
i
2
(
(
i
+
+
2
j
2
j
)
)
≤
16
(12)
>
16
where i and j are the DCT coefficient indices.
Taking the masking effect in the intra frame into account, the final contrast
masking factor is:
a
contrast
(
n i
, ,
j t
,
)
=
2
(
, in plain and edge region
(
C n i
, ,
)
(
j t a
T n i
, ,
,
⋅
min 4,max 1,
i
+
ψ
ψ
⋅
)
≤
16
2
j
)
j t
,
Lum
0.36
(
n t
,
)
(13)
, others
4. Simulation Results
4.1. Evaluation of the Improved JND Model Based on Transform
Domain
In order to verify the effectiveness of our proposed JND model based on DCT
domain, we selected eight test images of different contents and complexities as
shown in Figure 4 to carry out simulation experiments. Theoretical analysis
shows that under a certain visual quality, the larger the threshold of the JND
model is, the more visual redundancy will be excavated. Under the same injected
noise energy, a more accurate JND model leads to better perceived quality. In
order to verify the validity of the model, the thresholds calculated by the corres-
ponding JND models are introduced as noise into the DCT coefficients:
58
Journal of Computer and Communications
DOI: 10.4236/jcc.2018.64005
Q. M. Yi et al.
(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 4. Eight test images. (a) Bikes; (b) Buildings; (c) Caps; (d) House; (e) Monarch; (f)
Painted house; (g) Sailing 1; (h) Sailing 4.
C
noise
(
n i
, ,
j t
,
C n i
, ,
(
where,
coefficients after noise injection;
(
j t M
,
)
j t
n i
,
, ,
random
, ,n i jM
)
C
C n i
, ,
(
and
j t
,
)
)
+
=
noise
random
n i j
, ,
⋅
n i
JND , ,
(
j t
,
)
(14)
represent DCT coefficients and DCT
random takes +1 and −1.
The JND model presented in this paper is compared with the three models
shown in Table 1 respectively. As can be seen from the table, the PSNR meas-
ured by this model is the smallest. Under the same visual quality, the smaller the
PSNR value of the image is, the greater the energy is introduced into the noise
and the larger the corresponding JND threshold is. This means that the larger
JND threshold obtained by this model can tolerate more distortion, and the ac-
curacy of the model has been further improved.
4.2. The Overall Performance of the Perceptual Video Coding
Scheme
In order to make full use of the JND characteristics of the human visual sys-
tem to reduce the perceived redundancy of the input video, we integrated the
designed JND model into the HEVC coding framework. For the transform
skip mode, we chose the existing pixel domain JND model; and the proposed
JND model based on DCT domain is utilized for the transform non-skip
mode. Figure 5 shows the overall framework of the perceptual video coding
scheme.
In order to verify the effectiveness of the algorithm proposed in this paper, the
algorithm will be implemented on HM11.0, using the full I-frame encoding con-
figuration environment. The initial quantization parameters are set to 22, 27, 32
and 37, respectively. The test sequences used in the experiment include Kimono,
Cactus with a resolution of 1920 × 1080, BQMall, PartyScene with a resolution of
832 × 480, and Basketball Drill Text and China Speed for screen content encod-
ing. We will evaluate the performance of the algorithm in terms of bit number
reduction and encoding time. Compared to HM11.0, the bit rate reduction of the
perceptual video coding scheme and the encoding time are calculated by the fol-
lowing formula:
59
Journal of Computer and Communications
DOI: 10.4236/jcc.2018.64005
Q. M. Yi et al.
Table 1. PSNR between different models.
Test Image
Bikes
Buildings
Caps
House
Monarch
Painted House
Sailing1
Sailing4
Average
[8]
28.73
29.65
31.71
31.96
31.47
30.84
31.62
30.18
[14]
28.71
28.89
29.70
29.09
29.80
29.08
28.88
29.05
30.770
29.150
PSNR
[16]
27.36
28.09
31.23
29.48
31.43
28.35
29.20
28.75
29.236
Prop
25.85
24.87
26.12
25.81
26.15
25.74
25.44
25.91
25.736
Figure 5. Overall coding framework.
Bitrate
∆
=
Time
∆
=
Bitrate
Bitrate
ref
×
100%
(15)
ref
×
100%
(16)
Time
Pro
Time
−
Pro
Bitrate
−
Pro
Time
Pro
Table 2 shows the comparison of the performance of the proposed algorithm
and Chen’s [17] and Bae’s [4] schemes under different quantization parameters.
The experimental results show that compared with the algorithm of [4], the al-
gorithm reduces the encoding bit rate by 4.3%, compared with Chen’s algorithm,
the encoding bit rate decreases by up to 7.58%.
In order to more intuitively show the bitrate reduction of each algorithm,
Figure 6 shows the comparison of bitrates at different QP values. It can be ob-
60
Journal of Computer and Communications
DOI: 10.4236/jcc.2018.64005
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
