logo资料库

论文研究-静脉输液过程中滴速自动控制系统的建模与仿真 .pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.54M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 静脉输液过程中滴速自动控制系统的建模 与仿真# 杜启亮1,2，刘健豪1，董超2，田联房1* （1. 华南理工大学, 自动化科学与工程学院, 广州, 510641； 2. 国家海洋局, 南海维权技术与应用重点实验室, 广州, 510310） 摘要：为对静脉输液过程的滴速自动控制系统进行设计和分析，本文对此类型系统进行建模 和仿真研究。通过实验数据拟合出输液过程的静态模型，进而得到非线性的动态模型；采用 一阶惯性环节对执行机构的动态特性进行描述；采用定积分对基于红外光电对管的滴速检测 环节进行建模；在静态工作点对过程模型进行基于增量法的近似线性化处理，对给定值小范 围变化的情况设计了 PID 控制律，对给定值大范围变化的情况采用先开环控制后闭环控制 的控制策略。仿真结果表明，若系统在滴速较低的工作点附近工作，由于滴速测量值的更新 周期长，故动态调节时间明显比在滴速较高的工作点长。本文所建模型能较准确反映被控过 程和控制系统的特性，对控制系统的实施有较好的参考价值。 关键词：输液过程；滴速；建模；控制系统 中图分类号：TP273 Modeling and Simulation of an Automatic Drip Rate Control System on Intravenous Infusion Process DU Qiliang1,2, LIU Jianhao1, DONG Chao2, TIAN Lianfang1 (1. School of Automation Science and Engineering, South China University of Technology, Guangzhou, 510641; 2. Key Laboratory of Technology for Safeguarding of Maritime Rights and Interests and Application, State Oceanic Administration, Guangzhou, 510310) Abstract: To design and analyze an automatic drip rate control system on intravenous infusion process, this paper carried out researches on system modeling and simulation. A static model of the process, which was then used to calculate a nonlinear dynamic model, was obtained by experimental data after curve fitting. A first-order inertial element was utilized to depict the dynamics of the control element, while the infrared-photoelectric-based drip rate detection element was represented by a definite integral model. The process model was approximately linearized on quiescent operating points by incremental method, then a PID control law was designed for the case of small setting value changes while an open-loop-ahead closed loop strategy was presented for the case of large setting value changes. The simulation results showed the adjusting duration of the system when working on a quiescent operating point with relatively low drip rate was larger than when working with high drip rate, because lower drip rate resulted in longer update cycle due to the drip rate measurement mechanism. The presented model could reflect the actual characteristics of the controlled process and control system, which was a good reference to implementation of the control system. Key words: intravenous infusion process; drip rate; modeling; control system 5 10 15 20 25 30 35 40 0 引言 静脉输液器是常用的医疗设备，一般由输液瓶、静脉针、护帽、输液软管、药液过 滤器、流速调节器、滴壶、瓶塞穿刺器、进气管空气过滤器连接组成。其流量调节需 基金项目：国家海洋局南海维权技术与应用重点实验室 2012 年度开放基金(项目编号：1216)；高等学校博 士学科点专项科研基金新教师课题（项目编号：20120172120032） 作者简介：杜启亮（1980-），男，副研究员，主要研究方向：流程工业建模与控制. E-mail: qldu@scut.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn 45 要通过人手操作塑料夹持器收紧或放松输液软管来实现。如今，不少 特殊药物需要严 格控制输液速度，而输液速度往往受液体静压、穿刺点与调节液面的相对高度、病人体 位变化、所用药物性状、病人身体状况等诸多因素影响，需要在输液过程中进行动态调节。 医护人员要经常巡视并调整滴速，监视药液余量等。因此，开发自动化的输液过程控 制器，对于减轻医护人员繁重的工作压力有重要意义。 50 目前这类系统均采用数字化的控制技术。文献[1]利用 PLC 作为控制中心，利用激光传 感器进行非接触式液滴计量，利用调节吊瓶高度方法, 控制液滴的流量，并且实现了病房远 程网络监控。文献[2]采用 PC 机作为主机，以 AT89C52 单片机作为智能节点控制器，构成 一个分布式的主从局域控制网。本系统采用精度比较高的红外线光电传感器实现对液体点滴 速度的测量和液位监测，用永磁电机拖动、控制储液瓶的高度，实现点滴速度的自动调节。 55 文献[3]设计的输液滴速监视器，通过电极针将输液液滴转换成脉冲信号，以 C8051F236 高 速片上系统单片机为核心组成输液滴速监视器，仪器由脉冲检测、键盘、液晶显示、操作指 示和声光报警等单元组成。文献[4]以 MSP430 单片机为控制核心，采用模糊神经网络计算 调整量, 驱动步进电机控制挤紧器调整滴速，实现智能控制。其中信号传感方式采用了红外 光电传感器, 通过滤波消除杂散光干扰，原始信号的处理采用了锁相环倍频技术从而提高了 60 采样速度并缩短系统调整时间。文献[5]采用微波时域反射（Time-Domain Reflectometry, TDR）方法对液瓶中药液余量进行检测，在液瓶外贴两条电极，根据药液余量不同，两电极 之间介质的反射系数不同的原理，建立了测量模型。这些系统均能从功能上满足用户的需要， 但是对输液过程乃至整个控制系统的建模和分析工作少有提及。本文着重对该类型控制系统 进行分析，包括输液过程和检测环节的建模、控制器设计和整个系统的仿真。 65 1 控制系统设计 本文所述被控对象是一个过程，所以设计了一个典型的过程控制系统，主要由控制器、 执行器、控制对象、反馈环节组成，如图 1 所示。实施过程中系统的结构采用与文献[6]类 似的方式，示意图如图 2 所示。滴速是过程的被控变量，采用夹持器调节软管开度，即夹持 器开度作为过程的控制变量，电机及传动装置为执行机构（内嵌在夹持器内，图中未专门画 70 出），采用单片机作为控制器，采用光电传感器作为检测装置，检测原理参见文献[7]。 图 1 控制系统方块图 Fig.1 Block diagram of the control system 75 图 2 控制系统实施示意图 Fig.2 Illustrative implementation diagram of the control system - 2 - 检测装置控制器执行机构被控过程给定值输出
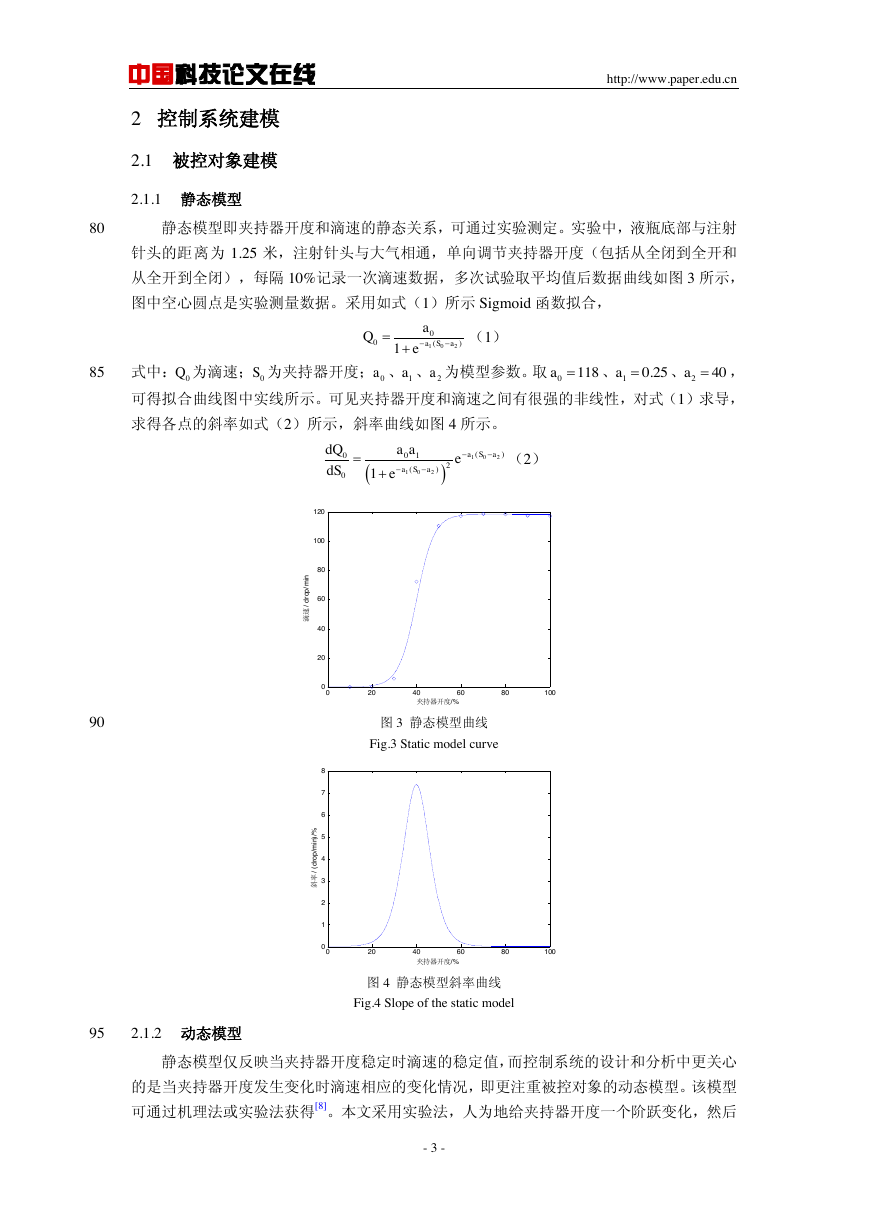
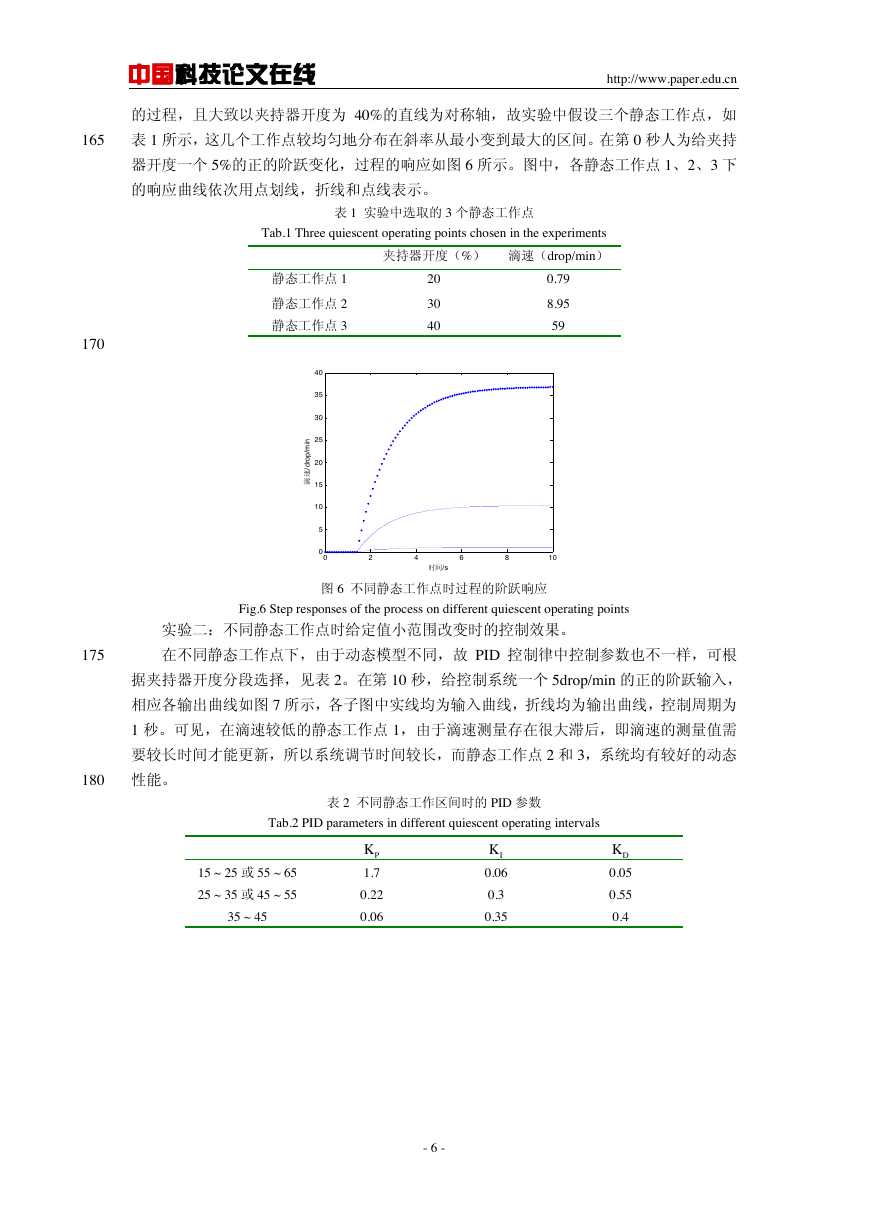
    中国科技论文在线 http://www.paper.edu.cn 2 控制系统建模 2.1 被控对象建模 2.1.1 静态模型 80 静态模型即夹持器开度和滴速的静态关系，可通过实验测定。实验中，液瓶底部与注射 针头的距离为 1.25 米，注射针头与大气相通，单向调节夹持器开度（包括从全闭到全开和 从全开到全闭），每隔 10%记录一次滴速数据，多次试验取平均值后数据曲线如图 3 所示， 图中空心圆点是实验测量数据。采用如式（1）所示 Sigmoid 函数拟合， （1） 85 式中： 为滴速； 为夹持器开度； 、 、 为模型参数。取 、 、 ， 可得拟合曲线图中实线所示。可见夹持器开度和滴速之间有很强的非线性，对式（1）求导， 求得各点的斜率如式（2）所示，斜率曲线如图 4 所示。 （2） 90 图 3 静态模型曲线 Fig.3 Static model curve 图 4 静态模型斜率曲线 Fig.4 Slope of the static model 95 2.1.2 动态模型 静态模型仅反映当夹持器开度稳定时滴速的稳定值，而控制系统的设计和分析中更关心 的是当夹持器开度发生变化时滴速相应的变化情况，即更注重被控对象的动态模型。该模型 可通过机理法或实验法获得[8]。本文采用实验法，人为地给夹持器开度一个阶跃变化，然后 - 3 - 10200()1aSaaQe0Q0S0a1a2a0118a10.25a240a102102()0012()01aSaaSadQaaedSe020406080100020406080100120夹持器开度/%滴速/ drop/min020406080100012345678夹持器开度/%斜率/ (drop/min)/%
    中国科技论文在线 http://www.paper.edu.cn 观察滴速的变化情况。根据观察结果，本文认为该过程可用一个一阶惯性环节串联一个纯滞 100 后环节来表示，如式（3）所示， （3） 式中： 、 分别为滴速的变化量 和夹持器开度的变化量 的拉氏变换； 、 分别为惯性时间常数和纯滞后时间常数； 为静态模型曲线中静态工作点处对应的斜率。 实际中观察得知，该过程的响应时间很快，故可取 。由于静态模型非线 105 性严重，故 的变化范围较大，可考虑基于增量法的近似线性化动态模型[9]，即在静态工作 点附近小范围区域内，取 为恒定值，其值等于静态工作点处的 值。 2.2 执行机构建模 执行器是步进电机及其驱动电路，它接收控制器的控制信号，将其转化为被控对象 的输入信号或动作。本文中执行机构由电机和传动机构组成。电机（包括其驱动电路） 110 根据控制器输出的信号转动相应的角度，传动机构将旋转运动转化为直线运动，直接推动夹 持器的阀杆。本文中所用电机为步进电机，一般步进电机的动态模型为二阶模型 [10]，考虑 到本系统中电机功率小，负载轻，故用一阶模型来近似描述。则执行机构的传递函数如式（4） 所示， （4） 115 式中： 为控制器输出的变化量 的拉氏变换。 为惯性时间常数，可选较小数值， 本文取 。 为放大系数，表示执行机构输出的直线运动位移量与输入的步进电机转 动角度的比值，与步进电机和传动机构的结构和参数有关。本文所选步进电机最小步长为 18°，通过实验测定得知每转动一圈，夹持器开度变化 2%，故选 。 2.3 检测装置建模 120 滴速检测装置是整个系统的关键环节，它需要对输液速度进行检测，对控制精度的影 响最大。输液器滴速的检测方法有接触式和非接触式两种，由于接触式的检测方法中检测装 置（如探针）需与药液接触容易污染药液，所以更常用的是非接触式的检测方法。本文采用 基于红外光电对管的非接触式滴速检测方法。发射管和接收管相对，轴向对齐，分别放置在 滴壶外两侧，并使轴线经过液滴下落的轨迹；若无液滴经过，发射管发射的红外光大部分能 125 到达接收管；若有液滴经过，由于光线发生了折射，故到达接收管的红外辐射能量将发生变 化；设计信号调理电路捕捉这种信号变化，然后输出到单片机系统，则可计算出两滴药液之 间的时间间隔，从而可知滴速[11]。 设滴速为 （drop/min），两滴之间的时间间隔为 （s），则两者关系如式（5）所示。 （5） 130 易知， 即为检测装置的采样周期，在控制系统运行期间，其将随 的变化而变化， 越小， 越大。也就是说，每隔 时间，滴速的测量值才能更新一次，而在 时间内，滴速的测量 值由采样保持器保持为上一个周期的测量值。因此在 时间内，测量值可能含有误差。假设 从 0 开始，按 1drop/(mins)的速率增加，见图 5（a），则 的测量值和相应的测量误差如 - 4 - 111()()1sKeQsSsTs()Qs()Ss()Qt()St1T11K11.5,0.5Tss1K1K1K22()()1KSsCsTs()Cs()Ct2T21Ts2K22Kddt0601dtdtddtdddtdtdtdtdd
    中国科技论文在线 http://www.paper.edu.cn 图 5（b）、（c）所示。可见，滴速越小，产生测量误差的概率越大。 135 140 (a) 滴速实际值 (a) Actual value of drip rate (b) 滴速测量值 (b) Measured value of drip rate 145 Fig.5 Illustrative diagram of measurement error of drip rate (c) 滴速测量误差 (c) Measurement error of drip rate 图 5 滴速的测量误差示意图 2.4 控制器建模 2.4.1 小范围改变给定值时的控制策略 设系统原工作在某静态工作点，当需要小范围改变给定值时，可将式（3）中的 值视 为原静态工作点处的值，设计 PID 控制器，如式（6）所示。 150 （6） 式中： 为误差 的拉氏变换； 、 、 分别为比例增益、积分增益和微分增益。 2.4.2 大范围改变给定值时的控制策略 当需要大范围改变给定值时，考虑到过程较强的非线性特性，采用先开环控制，后闭环 控制的策略。具体而言，当设定一个新的滴速给定值时，根据式（1）的静态模型计算出夹 155 持器开度，控制器输出控制信号，并一直保持，待滴速和夹持器开度稳定后，开环控制阶段 结束；此时再转入闭环控制，把此时的工作点作为静态工作点，采用上述小范围改变给定值 时的控制策略来进行控制，给定值为此时输出值和期望值的误差。其中滴速或夹持器开度是 否稳定可根据其变化率的值和持续时间来判断，具体而言，若滴速和夹持器开度变化率小于 某阈值 和 ，并且持续 ，则认为其稳定。 160 3 仿真实验 用 MATLAB 工具进行滴速过程控制系统的仿真，设计了 3 个实验进行仿真。 实验一：过程的建模与仿真实验。 观察图 4 曲线可知，静态模型的斜率变化随着夹持器开度的增加经历了从小变大再变小 - 5 - 0510152005101520时间/s实际滴速/ drop/min0510152005101520时间/s滴速测量值/ drop/min0510152001234时间/s误差/ drop/min1K()1()PPIPDCsKKKKKsEss()Es()EtPKIKDKdjLt
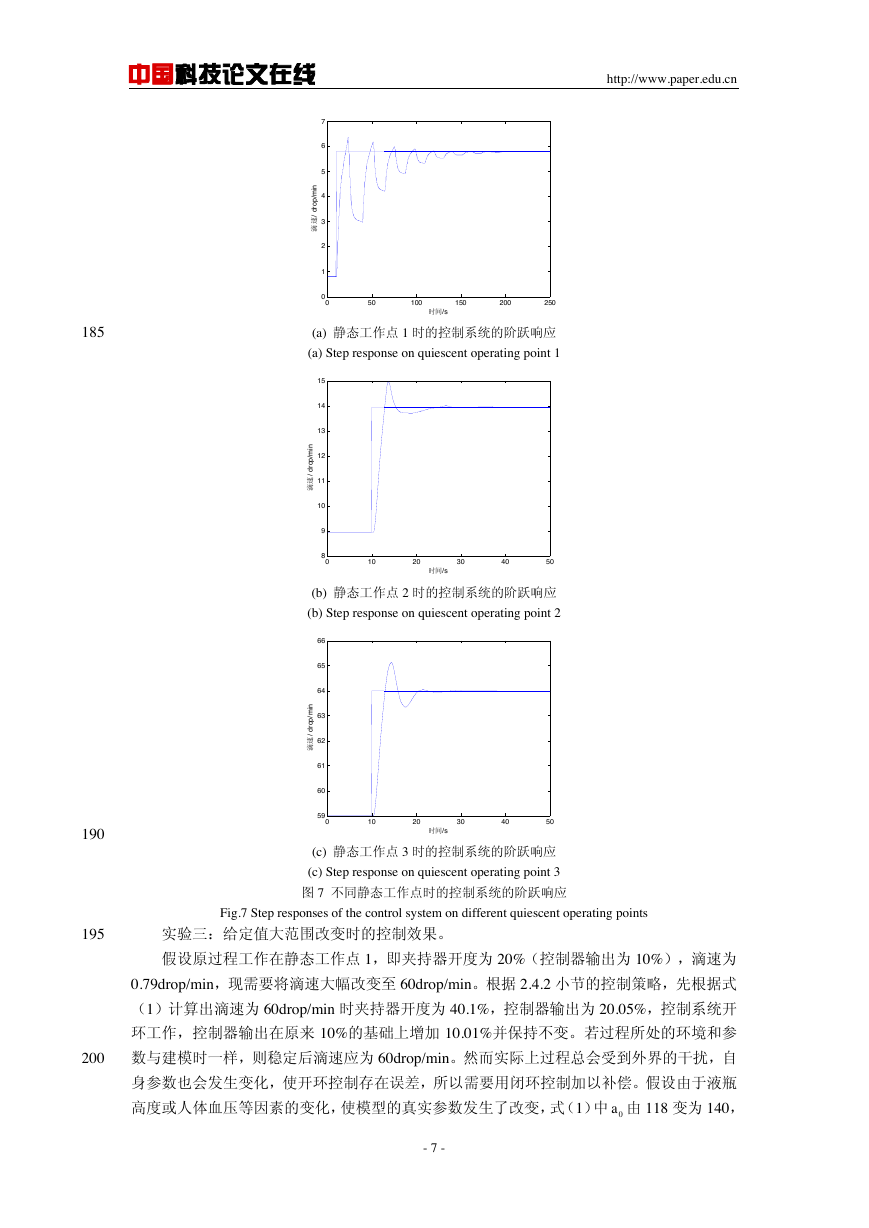
    中国科技论文在线 http://www.paper.edu.cn 的过程，且大致以夹持器开度为 40%的直线为对称轴，故实验中假设三个静态工作点，如 165 表 1 所示，这几个工作点较均匀地分布在斜率从最小变到最大的区间。在第 0 秒人为给夹持 器开度一个 5%的正的阶跃变化，过程的响应如图 6 所示。图中，各静态工作点 1、2、3 下 的响应曲线依次用点划线，折线和点线表示。 表 1 实验中选取的 3 个静态工作点 Tab.1 Three quiescent operating points chosen in the experiments 静态工作点 1 静态工作点 2 静态工作点 3 夹持器开度（%） 滴速（drop/min） 20 30 40 0.79 8.95 59 170 图 6 不同静态工作点时过程的阶跃响应 Fig.6 Step responses of the process on different quiescent operating points 实验二：不同静态工作点时给定值小范围改变时的控制效果。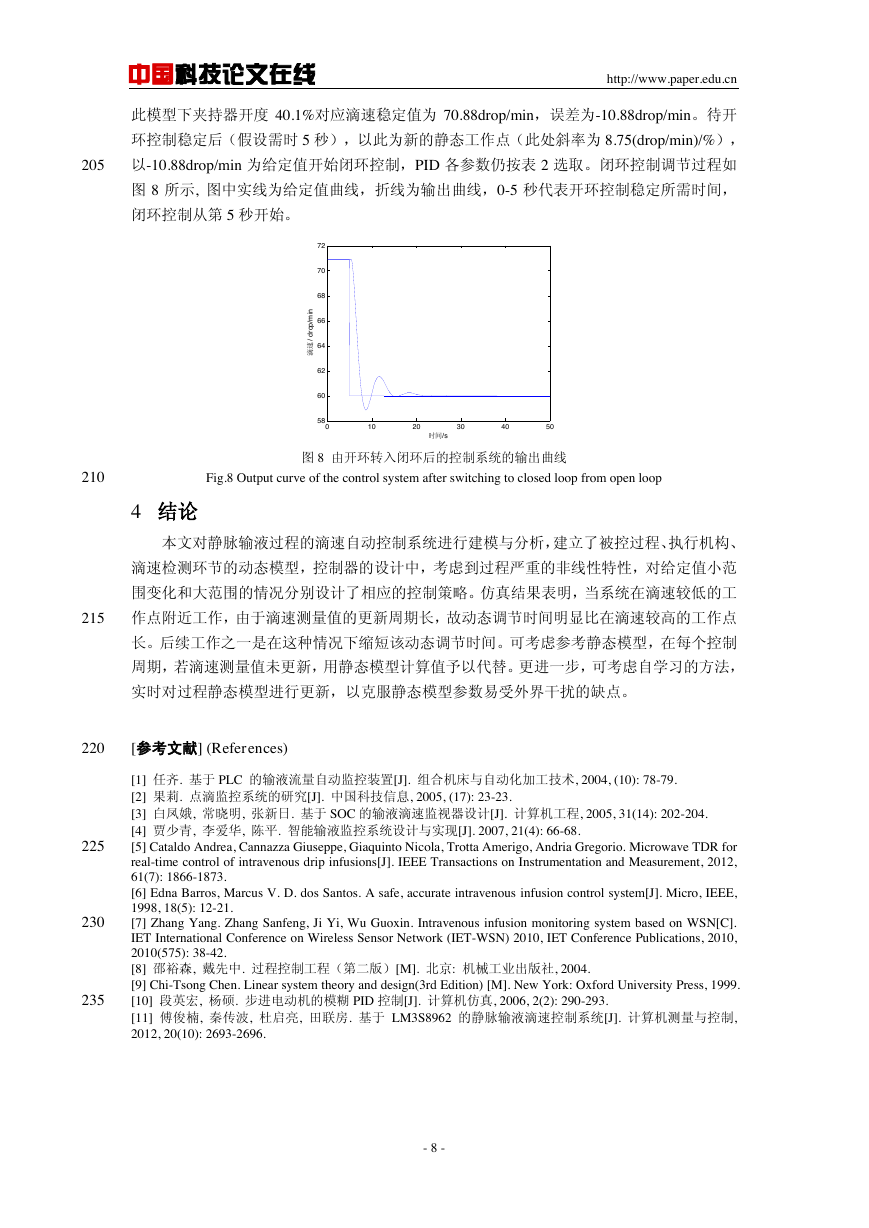 175 在不同静态工作点下，由于动态模型不同，故 PID 控制律中控制参数也不一样，可根 据夹持器开度分段选择，见表 2。在第 10 秒，给控制系统一个 5drop/min 的正的阶跃输入， 相应各输出曲线如图 7 所示，各子图中实线均为输入曲线，折线均为输出曲线，控制周期为 1 秒。可见，在滴速较低的静态工作点 1，由于滴速测量存在很大滞后，即滴速的测量值需 要较长时间才能更新，所以系统调节时间较长，而静态工作点 2 和 3，系统均有较好的动态 180 性能。 表 2 不同静态工作区间时的 PID 参数 Tab.2 PID parameters in different quiescent operating intervals 15 ~ 25 或 55 ~ 65 25 ~ 35 或 45 ~ 55 35 ~ 45 1.7 0.22 0.06 0.06 0.3 0.35 0.05 0.55 0.4 - 6 - 02468100510152025303540时间/s滴速/drop/minPKIKDK
    中国科技论文在线 http://www.paper.edu.cn 185 (a) 静态工作点 1 时的控制系统的阶跃响应 (a) Step response on quiescent operating point 1 (b) 静态工作点 2 时的控制系统的阶跃响应 (b) Step response on quiescent operating point 2 190 (c) 静态工作点 3 时的控制系统的阶跃响应 (c) Step response on quiescent operating point 3 图 7 不同静态工作点时的控制系统的阶跃响应 195 实验三：给定值大范围改变时的控制效果。 Fig.7 Step responses of the control system on different quiescent operating points 假设原过程工作在静态工作点 1，即夹持器开度为 20%（控制器输出为 10%），滴速为 0.79drop/min，现需要将滴速大幅改变至 60drop/min。根据 2.4.2 小节的控制策略，先根据式 （1）计算出滴速为 60drop/min 时夹持器开度为 40.1%，控制器输出为 20.05%，控制系统开 环工作，控制器输出在原来 10%的基础上增加 10.01%并保持不变。若过程所处的环境和参 200 数与建模时一样，则稳定后滴速应为 60drop/min。然而实际上过程总会受到外界的干扰，自 身参数也会发生变化，使开环控制存在误差，所以需要用闭环控制加以补偿。假设由于液瓶 高度或人体血压等因素的变化，使模型的真实参数发生了改变，式（1）中 由 118 变为 140， - 7 - 05010015020025001234567时间/s滴速/ drop/min0102030405089101112131415时间/s滴速/ drop/min010203040505960616263646566时间/s滴速/ drop/min0a
    中国科技论文在线 http://www.paper.edu.cn 此模型下夹持器开度 40.1%对应滴速稳定值为 70.88drop/min，误差为-10.88drop/min。待开 环控制稳定后（假设需时 5 秒），以此为新的静态工作点（此处斜率为 8.75(drop/min)/%）， 205 以-10.88drop/min 为给定值开始闭环控制，PID 各参数仍按表 2 选取。闭环控制调节过程如 图 8 所示, 图中实线为给定值曲线，折线为输出曲线，0-5 秒代表开环控制稳定所需时间， 闭环控制从第 5 秒开始。 210 Fig.8 Output curve of the control system after switching to closed loop from open loop 图 8 由开环转入闭环后的控制系统的输出曲线 4 结论 本文对静脉输液过程的滴速自动控制系统进行建模与分析，建立了被控过程、执行机构、 滴速检测环节的动态模型，控制器的设计中，考虑到过程严重的非线性特性，对给定值小范 围变化和大范围的情况分别设计了相应的控制策略。仿真结果表明，当系统在滴速较低的工 215 作点附近工作，由于滴速测量值的更新周期长，故动态调节时间明显比在滴速较高的工作点 长。后续工作之一是在这种情况下缩短该动态调节时间。可考虑参考静态模型，在每个控制 周期，若滴速测量值未更新，用静态模型计算值予以代替。更进一步，可考虑自学习的方法， 实时对过程静态模型进行更新，以克服静态模型参数易受外界干扰的缺点。 220 [参考文献] (References) [1] 任齐. 基于 PLC 的输液流量自动监控装置[J]. 组合机床与自动化加工技术, 2004, (10): 78-79. [2] 果莉. 点滴监控系统的研究[J]. 中国科技信息, 2005, (17): 23-23. [3] 白凤娥, 常晓明, 张新日. 基于 SOC 的输液滴速监视器设计[J]. 计算机工程, 2005, 31(14): 202-204. [4] 贾少青, 李爱华, 陈平. 智能输液监控系统设计与实现[J]. 2007, 21(4): 66-68. [5] Cataldo Andrea, Cannazza Giuseppe, Giaquinto Nicola, Trotta Amerigo, Andria Gregorio. Microwave TDR for real-time control of intravenous drip infusions[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(7): 1866-1873. [6] Edna Barros, Marcus V. D. dos Santos. A safe, accurate intravenous infusion control system[J]. Micro, IEEE, 1998, 18(5): 12-21. [7] Zhang Yang. Zhang Sanfeng, Ji Yi, Wu Guoxin. Intravenous infusion monitoring system based on WSN[C]. IET International Conference on Wireless Sensor Network (IET-WSN) 2010, IET Conference Publications, 2010, 2010(575): 38-42. [8] 邵裕森, 戴先中. 过程控制工程（第二版）[M]. 北京: 机械工业出版社, 2004. [9] Chi-Tsong Chen. Linear system theory and design(3rd Edition) [M]. New York: Oxford University Press, 1999. [10] 段英宏, 杨硕. 步进电动机的模糊 PID 控制[J]. 计算机仿真, 2006, 2(2): 290-293. [11] 傅俊楠, 秦传波, 杜启亮, 田联房. 基于 LM3S8962 的静脉输液滴速控制系统[J]. 计算机测量与控制, 2012, 20(10): 2693-2696. 225 230 235 - 8 - 010203040505860626466687072时间/s滴速/ drop/min
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料