logo资料库

非常浅显易懂的傅里叶变换讲解，让你理解为什么要做傅里叶变换.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.40M 资料格式：pdf 举报 版权申诉
第1页 / 共21页
第2页 / 共21页
第3页 / 共21页
第4页 / 共21页
第5页 / 共21页
第6页 / 共21页
第7页 / 共21页
第8页 / 共21页
资料共21页，剩余部分请下载后查看
    理解离散傅立叶变换（一） ------傅立叶变换的由来 关于傅立叶变换，无论是书本还是在网上可以很容易找到关于傅立叶变换的描述，但是 大都是些故弄玄虚的文章，太过抽象，尽是一些让人看了就望而生畏的公式的罗列，让人很 难能够从感性上得到理解，最近，我偶尔从网上看到一个关于数字信号处理的电子书籍，是 一个叫 Steven W. Smith, Ph.D.外国人写的，写得非常浅显，里面有七章由浅入深地专门 讲述关于离散信号的傅立叶变换，虽然是英文文档，我还是硬着头皮看完了有关傅立叶变换 的有关内容，看了有茅塞顿开的感觉，在此把我从中得到的理解拿出来跟大家分享，希望很 多被傅立叶变换迷惑的朋友能够得到一点启发，这电子书籍是免费的，有兴趣的朋友也可以 从网上下载下来看一下，URL 地址是： http://www.dspguide.com/pdfbook.htm 要理解傅立叶变换，确实需要一定的耐心，别一下子想着傅立叶变换是怎么变换的，当 然，也需要定的高等数学基础，最基本的是级数变换，其中傅立叶级数变换是傅立叶变换的 基础公式。 一、傅立叶变换的提出 让我们先看看为什么会有傅立叶变换？傅立叶是一位法国数学家和物理学家的名字，英 语原名是 Jean Baptiste Joseph Fourier(1768-1830), Fourier 对热传递很感兴趣，于 1807 年在法 国科学学会上发表了一篇论文，运用正弦曲线来描述温度分布，论文里有个在当时具有争议 性的决断：任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人， 其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯 (Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其它审查者投票通过并要发表这个论文 时，拉格朗日坚决反对，在近 50 年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带 有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，拒 绝了傅立叶的工作，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远 征埃及，法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后 15 年这个论文 才被发表出来。 谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们 可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立 叶是对的。 为什么我们要用正弦曲线来代替原来的曲线呢？如我们也还可以用方波或三角波来代 替呀，分解信号的方法是无穷的，但分解信号的目的是为了更加简单地处理原来的信号。用 正余弦来表示原信号会更加简单，因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。 一个正弦曲线信号输入后，输出的仍是正弦曲线，只有幅度和相位可能发生变化，但是频率 和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质，正因如此我们才不用方波或三 角波来表示。 二、傅立叶变换分类 1
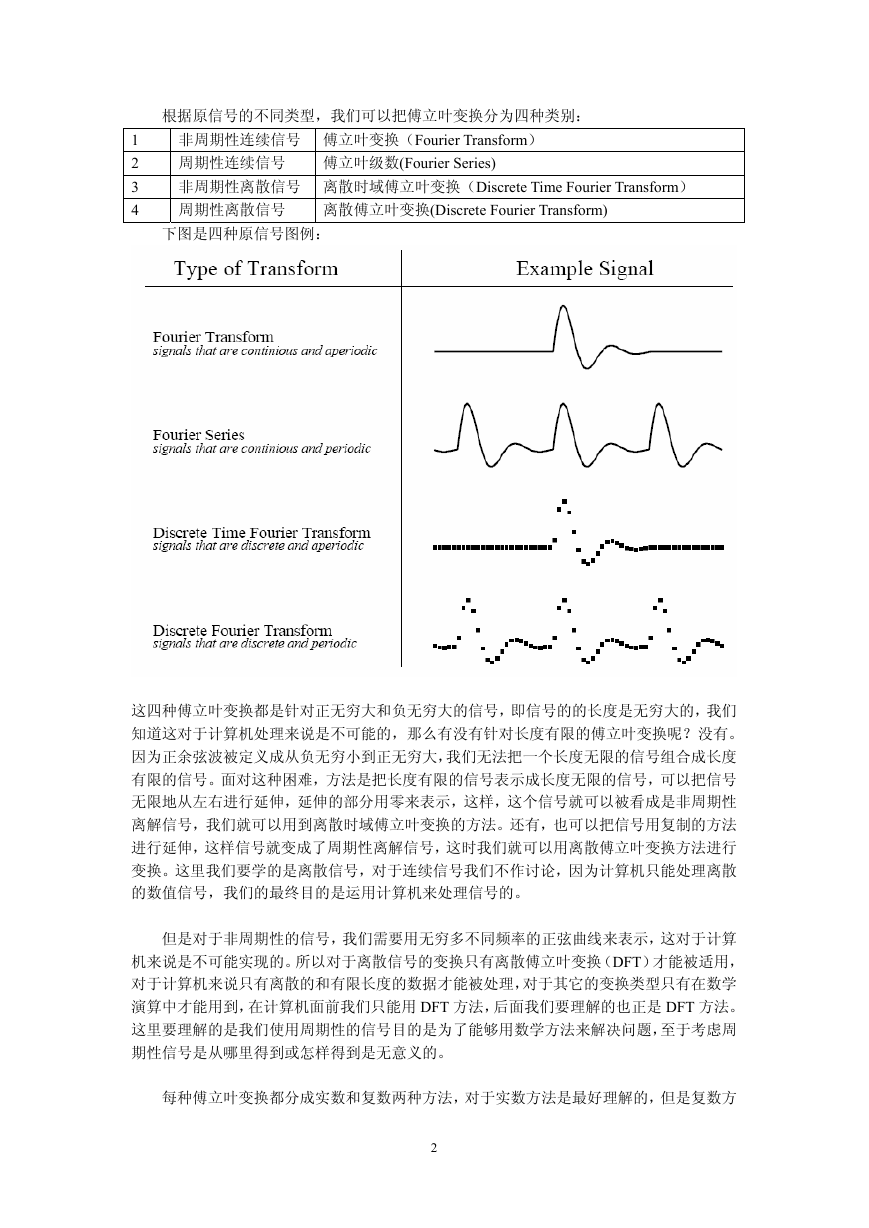
    根据原信号的不同类型，我们可以把傅立叶变换分为四种类别： 1 2 3 4 下图是四种原信号图例： 非周期性连续信号 傅立叶变换（Fourier Transform） 周期性连续信号 非周期性离散信号 离散时域傅立叶变换（Discrete Time Fourier Transform） 周期性离散信号 傅立叶级数(Fourier Series) 离散傅立叶变换(Discrete Fourier Transform) 这四种傅立叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，我们 知道这对于计算机处理来说是不可能的，那么有没有针对长度有限的傅立叶变换呢？没有。 因为正余弦波被定义成从负无穷小到正无穷大，我们无法把一个长度无限的信号组合成长度 有限的信号。面对这种困难，方法是把长度有限的信号表示成长度无限的信号，可以把信号 无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性 离解信号，我们就可以用到离散时域傅立叶变换的方法。还有，也可以把信号用复制的方法 进行延伸，这样信号就变成了周期性离解信号，这时我们就可以用离散傅立叶变换方法进行 变换。这里我们要学的是离散信号，对于连续信号我们不作讨论，因为计算机只能处理离散 的数值信号，我们的最终目的是运用计算机来处理信号的。 但是对于非周期性的信号，我们需要用无穷多不同频率的正弦曲线来表示，这对于计算 机来说是不可能实现的。所以对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用， 对于计算机来说只有离散的和有限长度的数据才能被处理，对于其它的变换类型只有在数学 演算中才能用到，在计算机面前我们只能用 DFT 方法，后面我们要理解的也正是 DFT 方法。 这里要理解的是我们使用周期性的信号目的是为了能够用数学方法来解决问题，至于考虑周 期性信号是从哪里得到或怎样得到是无意义的。 每种傅立叶变换都分成实数和复数两种方法，对于实数方法是最好理解的，但是复数方 2
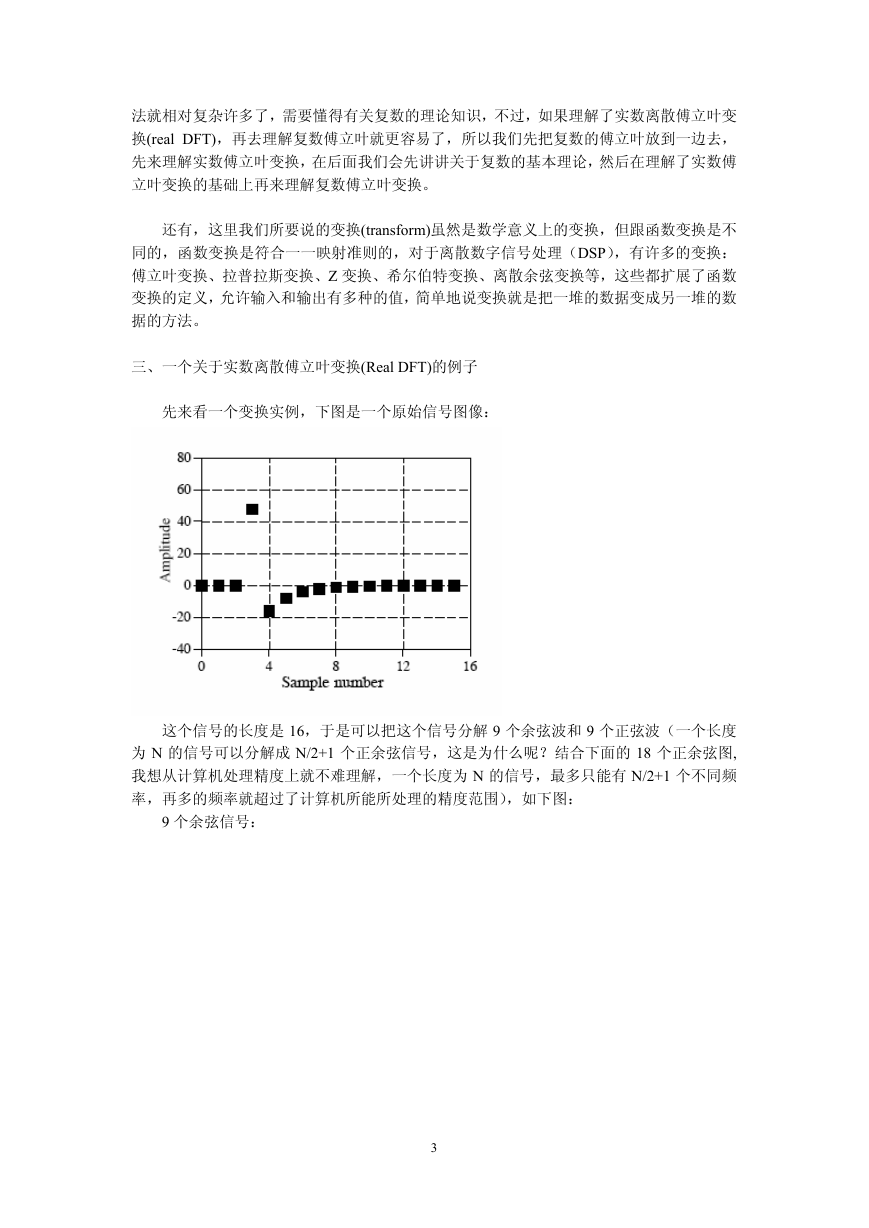
    法就相对复杂许多了，需要懂得有关复数的理论知识，不过，如果理解了实数离散傅立叶变 换(real DFT)，再去理解复数傅立叶就更容易了，所以我们先把复数的傅立叶放到一边去， 先来理解实数傅立叶变换，在后面我们会先讲讲关于复数的基本理论，然后在理解了实数傅 立叶变换的基础上再来理解复数傅立叶变换。 还有，这里我们所要说的变换(transform)虽然是数学意义上的变换，但跟函数变换是不 同的，函数变换是符合一一映射准则的，对于离散数字信号处理（DSP），有许多的变换： 傅立叶变换、拉普拉斯变换、Z 变换、希尔伯特变换、离散余弦变换等，这些都扩展了函数 变换的定义，允许输入和输出有多种的值，简单地说变换就是把一堆的数据变成另一堆的数 据的方法。 三、一个关于实数离散傅立叶变换(Real DFT)的例子 先来看一个变换实例，下图是一个原始信号图像： 这个信号的长度是 16，于是可以把这个信号分解 9 个余弦波和 9 个正弦波（一个长度 为 N 的信号可以分解成 N/2+1 个正余弦信号，这是为什么呢？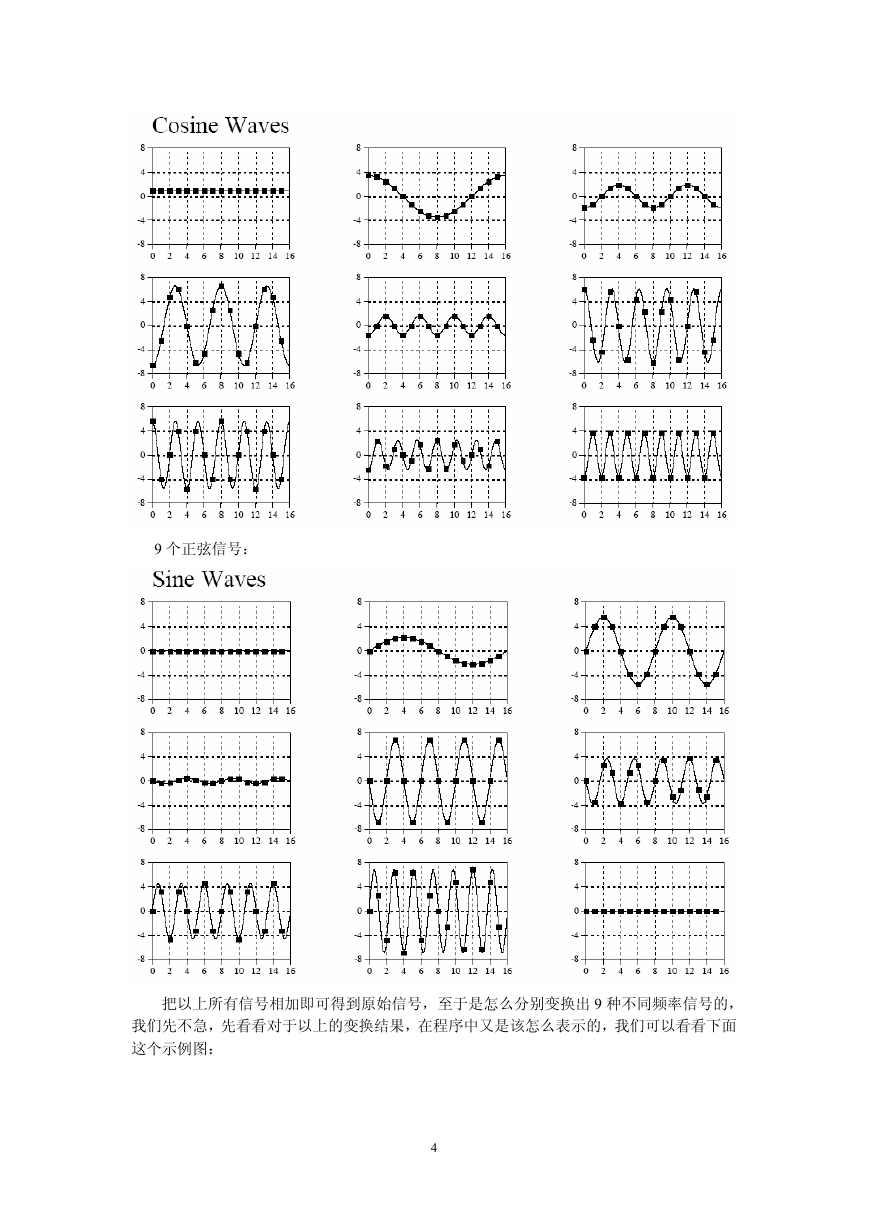结合下面的 18 个正余弦图, 我想从计算机处理精度上就不难理解，一个长度为 N 的信号，最多只能有 N/2+1 个不同频 率，再多的频率就超过了计算机所能所处理的精度范围），如下图： 9 个余弦信号： 3
    9 个正弦信号： 把以上所有信号相加即可得到原始信号，至于是怎么分别变换出 9 种不同频率信号的， 我们先不急，先看看对于以上的变换结果，在程序中又是该怎么表示的，我们可以看看下面 这个示例图： 4
    上图中左边表示时域中的信号，右边是频域信号表示方法，从左向右表示正向转换 (Forward DFT)，从右向左表示逆向转换(Inverse DFT)，用小写 x[]表示信号在每个时间点上 的幅度值数组, 用大写 X[]表示每种频率的副度值数组, 因为有 N/2+1 种频率，所以该数组 长度为 N/2+1，X[]数组又分两种，一种是表示余弦波的不同频率幅度值：Re X[]，另一种是 表示正弦波的不同频率幅度值：Im X[]，Re 是实数(Real)的意思，Im 是虚数(Imagine)的意思， 采用复数的表示方法把正余弦波组合起来进行表示，但这里我们不考虑复数的其它作用，只 记住是一种组合方法而已，目的是为了便于表达（在后面我们会知道，复数形式的傅立叶变 换长度是 N，而不是 N/2+1）。 下一节我们将来看一下实数傅立叶变换的具体方法。 理解离散傅立叶变换（二） ------实数形式离散傅立叶变换（Real DFT） 上一节我们看到了一个实数形式离散傅立叶变换的例子，通过这个例子能够让我们先对 傅立叶变换有一个较为形象的感性认识，现在就让我们来看看实数形式离散傅立叶变换的正 向和逆向是怎么进行变换的。在此，我们先来看一下频率的多种表示方法。 一、 频域中关于频率的四种表示方法 1、 序号表示方法，根据时域中信号的样本数取 0 ~ N/2，用这种方法在程序中使用起来 可以更直接地取得每种频率的幅度值，因为频率值跟数组的序号是一一对应的: X[k]，取值范围是 0 ~ N/2； 2、 分数表示方法，根据时域中信号的样本数的比例值取 0 ~ 0.5: X[ƒ]，ƒ = k/N，取值 范围是 0 ~ 1/2； 3、 用弧度值来表示，把 ƒ 乘以一个 2π 得到一个弧度值，这种表示方法叫做自然频率 (natural frequency)：X[ω]，ω = 2πƒ = 2πk/N，取值范围是 0 ~ π； 4、 以赫兹(Hz)为单位来表示，这个一般是应用于一些特殊应用，如取样率为 10 kHz 表示每秒有 10,000 个样本数：取值范围是 0 到取样率的一半。 二、 DFT 基本函数 5
    ck[i] = cos(2πki/N) sk[i] = sin(2πki/N) 其中 k 表示每个正余弦波的频率，如为 2 表示在 0 到 N 长度中存在两个完整的周期，10 即有 10 个周期，如下图： 上图中至于每个波的振幅(amplitude)值(Re X[k],Im X[k])是怎么算出来的,这个是 DFT 的 核心，也是最难理解的部分，我们先来看看如何把分解出来的正余弦波合成原始信号(Inverse DFT)。 三、 合成运算方法(Real Inverse DFT) DFT 合成等式： 如果有学过傅立叶级数，对这个等式就会有似曾相识的感觉，不错！这个等式跟傅立叶 级数是非常相似的： 当然，差别是肯定是存在的，因为这两个等式是在两个不同条件下运用的，至于怎 么证明 DFT 合成公式，这个我想需要非常强的高等数学理论知识了，这是研究数学的 人的工作，对于普通应用者就不需要如此的追根究底了，但是傅立叶级数是好理解的， 6
    我们起码可以从傅立叶级数公式中看出 DFT 合成公式的合理性。 DFT 合成等式中的 Im 转换方法: __ X [k]和 Re __ X [k]跟 Im X[k]和 Re X[k]是不一样的，下面是 但 k 等于 0 和 N/2 时,实数部分的计算要用下面的等式: 上面四个式中的 N 是时域中点的总数，k 是从 0 到 N/2 的序号。 为什么要这样进行转换呢？这个可以从频谱密度(spectral density)得到理解，如下图 就是个频谱图： 这是一个频谱图，横坐标表示频率大小，纵坐标表示振幅大小，原始信号长度为 N （这里是 32），经 DFT 转换后得到的 17 个频率的频谱，频谱密度表示每单位带宽中为 多大的振幅，那么带宽是怎么计算出来的呢？看上图，除了头尾两个，其余点的所占的 宽度是 2/N，这个宽度便是每个点的带宽，头尾两个点的带宽是 1/N,而 Im X[k]和 Re X[k] 表示的是频谱密度，即每一个单位带宽的振幅大小，但 Im __ X [k]和 Re __ X [k]表示 2/N （或 1/N）带宽的振幅大小，所以 Im 的 2/N（或 1/N）。 __ X [k]和 Re __ X [k]分别应当是 Im X[k]和 Re X[k] 频谱密度就象物理中物质密度，原始信号中的每一个点就象是一个混合物，这个混 7
    合物是由不同密度的物质组成的，混合物中含有的每种物质的质量是一样的，除了最大 和最小两个密度的物质外，这样我们只要把每种物质的密度加起来就可以得到该混合物 的密度了，又该混合物的质量是单位质量，所以得到的密度值跟该混合物的质量值是一 样的。 至于为什么虚数部分是负数，这是为了跟复数 DFT 保持一致，这个我们将在后面 会知道这是数学计算上的需要（Im X[k]计算时加上了一个负号，Im 结果便是正的，等于没有变化）。 如果已经得到了 DFT 结果，这时要进行逆转换，即合成原始信号，则可按如下步 骤进行转换： __ X [k]再加上负号， __ X [k]和 Re __ X [k]的值； 1、 先根据上面四个式子计算得出 Im 2、 再根据 DFT 合成等式得到原始信号数据。 下面是用 BASIC 语言来实现的转换源代码： 100 ‘DFT 逆转换方法 110 ‘/XX[]数组存储计算结果（时域中的原始信号） 120 ‘/REX[]数组存储频域中的实数分量，IMX[]为虚分量 130 ‘ 140 DIM XX[511] 150 DIM REX[256] 160 DIM IMX[256] 170 ‘ 180 PI = 3.14159265 190 N% = 512 200 ‘ 210 GOSUB XXXX ‘转到子函数去获取 REX[]和 IMX[]数据 220 ‘ 230 ‘ 240 ‘ 250 FOR K% = 0 TO 256 260 REX[K%] = REX[K%] / (N%/2) 270 IMX[K%] = -IMX[K%] / (N%/2) 280 NEXT k% 290 ‘ 300 REX[0] = REX[0] / N 310 REX[256] = REX[256] / N 320 ‘ 330 ‘ 初始化 XX[]数组 340 FOR I% = 0 TO 511 350 XX[I%] = 0 360 NEXT I% 370 ‘ 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料