logo资料库

2013北航应用数理统计第一次大作业-回归分析.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.21M 资料格式：doc 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    关于影响财政收入因素的回归分析
    摘要
    财政是同国家的产生和存在紧密相连的，财政收入是衡量一个国家财力的重要指标，是实现国家职能的财力保证，
    应用数理统计 第一次大作业 关于影响财政收入因素的回归分析 院 系 名 称 专 业 名 称 学 生 姓 名 学 号 任 课 教 师
    关于影响财政收入因素的回归分析 摘要 财政是同国家的产生和存在紧密相连的，财政收入是衡量一个国家财力的重 要指标，是实现国家职能的财力保证，关系到社会经济发展和人民生活水平的提 高，政府在社会经济活动中提供的公共物品和服务的范围和数量在很大程度上决 定于财政收入的充裕状况。本文通过调研了解了一些对财政收入影响的因素，并 在《中国统计年鉴》和《中国统计摘要》上查找二十多年来我国财政收入，以及 相关影响因素的统计，通过多元线性回归分析和逐步回归法对各影响因素进行建 模，借助SPSS 统计分析工具对相关的统计数据进行处理分析，建立能够反映财 政收入和各影响因素之间的最优回归方程，并结合实际情况对得到的模型进行合 理性分析和解释。 关键词 财政收入，多元线性回归，逐步回归法，SPSS 1. 引言 财政作为一国政府的活动,是政府职能的具体体现,主要有资源配置、收入再 分配和宏观经济调控三大职能。财政收入是政府部门的公共收入,是国民收入分 配中用于保证政府行使其公共职能、实施公共政策以及提供公共服务的资金需 求。财政收入的增长情况关系着一个国家经济的发展和社会的进步。对国家财政 的收入状况进行研究是十分必要的。 研究财政收入的影响因素离不开一些基本的经济变量。大多数相关的研究文 献中都把各项税收这个指标作为影响财政收入的基本因素,还有一些文献中也提 出了其他一些变量, 比如社会消费品零售总额、人口状况、第一产业的发展情况、 第二产业的发展情况、第三产业的发展情况等。影响财政收入的因素众多复杂, 但 是通过研究经济理论对财政收入的解释以及对实践的观察, 对财政收入影响的因 素主要有总税收、各项税收、企业所得税和就业人数等。为了研究影响国家财政 收入的因素，很有必要对财政收入和影响财政收入的因素作必要的认识，如果能 对他们之间的关系作一下回归，并利用所知道的数据建立起回归模型这对研究财 政收入很有意义。 由于统计数据限制，本文选取了 1990-2012 年间的年度财政收入及主要影响 因素的数据，包括工业，农业，建筑业，社会消费品零售总额，人口总数等，运 用回归分析方法，通过 SPSS 软件对这些因素与就业人数之间的线性关系进行分 析，寻找其中潜在的关系。 2. 解决问题的方法和计算结果 2.1 要解决的问题与数据采集 财政收入是社会各种因素相互影响相互作用的结果，本文从财政收入的部门 构成来分析财政收入的影响因素。从国民经济部门结构看，财政收入又表现为来
    自各经济部门的收入。财政收入的部门构成就是在财政收入中，由来自国民经济 各部门的收入所占的不同比例来表现财政收入来源的结构，它体现国民经济各部 门与财政收入的关系。我国财政收入主要来自于工业、农业、商业、交通运输和 服务业等部门，其中工业和农业对财政收入的影响最大。 本文在进行统计时，查阅《中国统计年鉴 2013》[2]和《中国统计摘要》[3]中 收录的 1990 年至 2012 年的全国财政收入为因变量，初步选取各项税收、工业总 产值、建筑业总产值、农业总产值、社会消费品零售总额、人口总数、受灾面积、 国内生产总值为自变量，分析它们之间的联系，如表 1 所示。 表 1： 1990 年-2012 年间财政收入与相关影响因素统计表 年份 财政收入 工 业 总 产值 建 筑 业 总产值 农 业 总 产值 人口数 受灾 面积 国内生产 总值 各项税收 5062 5342.2 5866.6 6963.8 9572.7 12135.8 14015.4 14441.9 14817.6 14770 14944.7 15781.3 16537 17381.7 21412.7 22420 24040 28627 33702 35226 40533.6 47486.2 52373.6 6858 8087.1 10284.5 14188 19480.7 24950.6 29447.6 32921.4 34018.4 35861.5 40033.6 43580.6 47431.3 54945.5 65210 77230.8 91310.9 110534.9 130260.2 135239.9 160722.2 188470.2 199670.7 2937.1 3149.48 3483.37 4348.95 5218.1 6242.2 7407.99 8651.14 9875.95 11444.08 13395.23 16386.04 18903.64 21715.25 26396.47 31649.29 38760.2 51321.78 61330.35 68518.3 83101.51 103874.43 117253.52 本文首先对上述数据通过使用 SPSS 软件做数据散点图，观察每个影响因素 与就业人数之间的关系，是否具有线性特点；然后通过逐步回归过程，在偏 F 检验显著的前提下，去除模型中不显著的变量，最终建立对财政收入有显著影响 的线性回归模型。 18667.8 21781.5 26923.5 35333.9 48197.9 60793.7 71176.6 78973.0 84402.3 89677.1 99214.6 109655.2 120332.7 135822.8 159878.3 184937.4 216314.4 265810.3 314045.4 340902.8 401512.8 473104.0 518942.1 114333 115823 117171 118517 119850 121121 122389 123626 124761 125786 126743 127627 128453 129227 129988 130756 131448 132129 132802 133450 134091 134735 135404 3847 5547 5133 4883 5504 4582 4699 5343 5015 4998 5469 5221 4695 5451 3711 3882 4109 4899 3999 4721 3743 3247 2496 2821.86 2990.17 3296.91 4255.30 5126.88 6038.04 6909.82 8234.04 9262.80 10682.58 12581.51 15301.38 17636.45 20017.31 24165.68 28778.54 34804.35 45621.97 54223.79 59521.59 73210.79 89738.39 100614.28 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 社 会 消 费 品 零 售总额 8300.1 9415.6 10993.7 14270.4 18622.9 23613.8 28360.2 31252.9 33378.1 35647.9 39105.7 43055.4 48135.9 52516.3 59501 68352.6 79145.2 93571.6 114830.1 132678.4 156998.4 183918.6 210307 859.4 1015.1 1415 2266.5 2964.7 3728.8 4387.4 4621.6 4985.8 5172.1 5522.3 5931.7 6465.5 7490.8 8694.3 10367.3 12408.6 15296.5 18743.2 22398.8 26661 31942.7 35491.3 2.2 模型建立与分析 2.2.1 变量选取
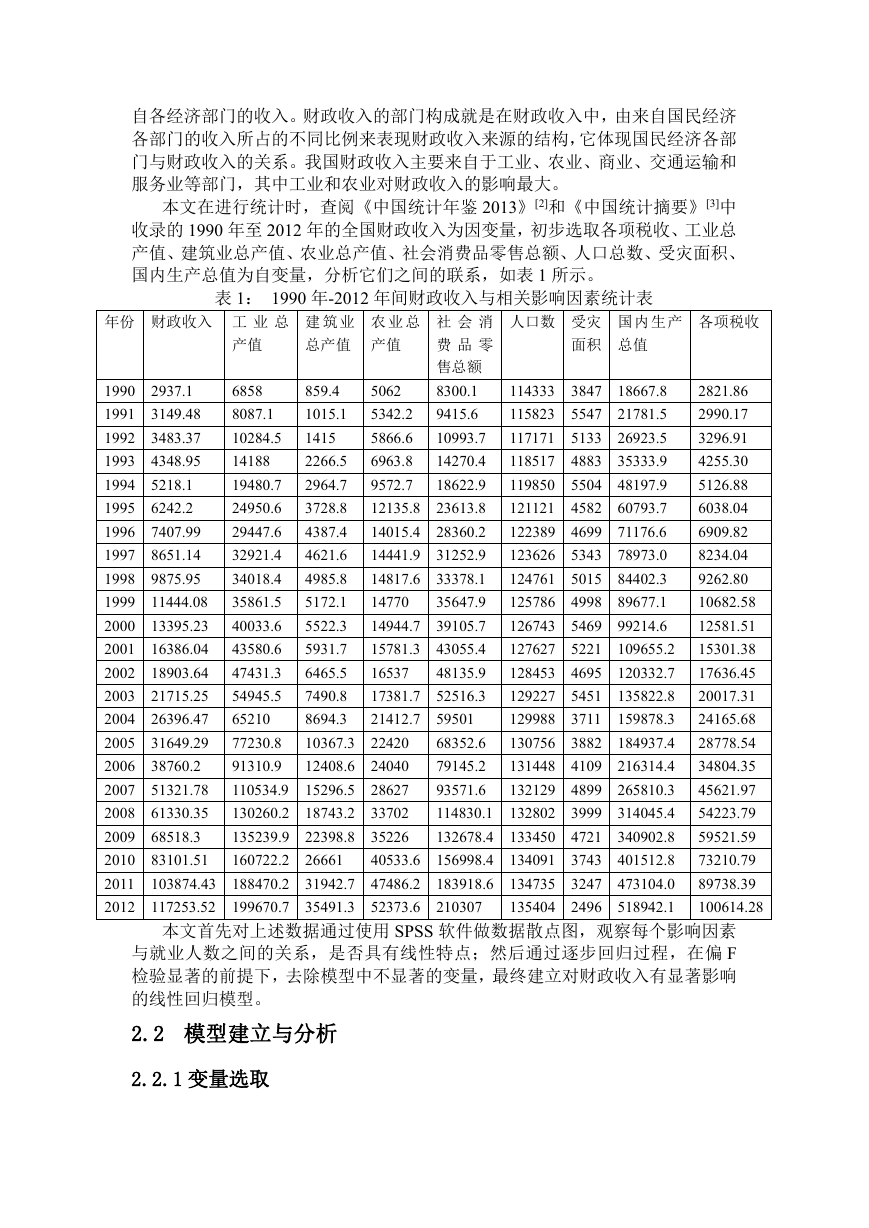
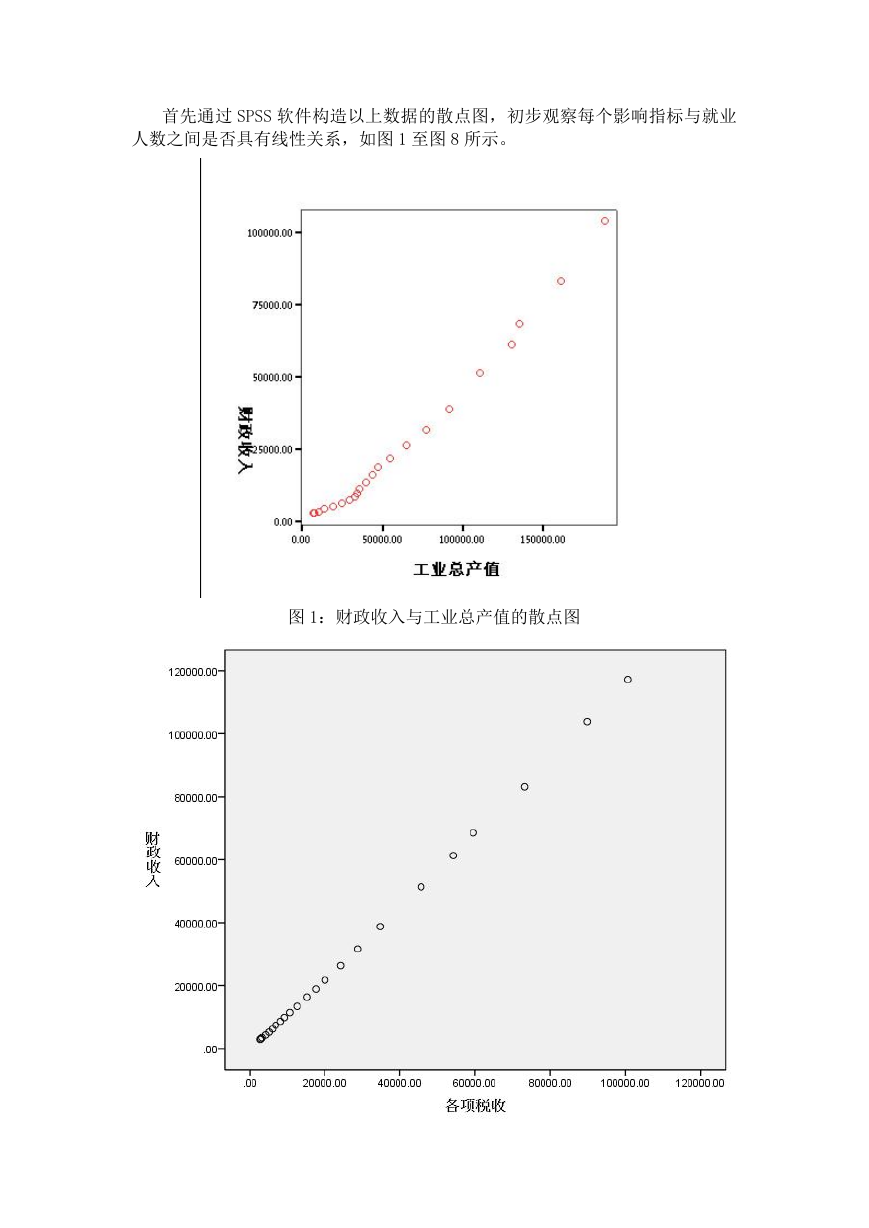
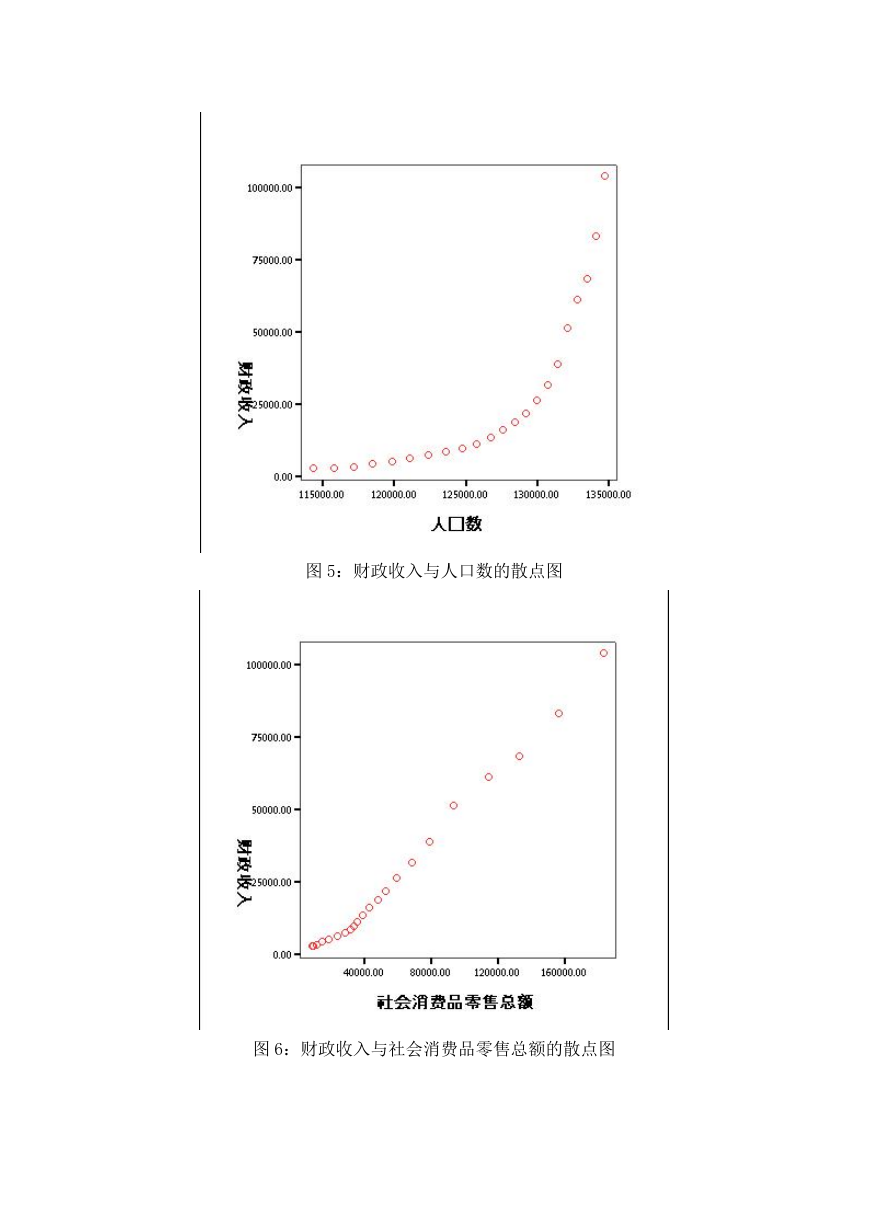
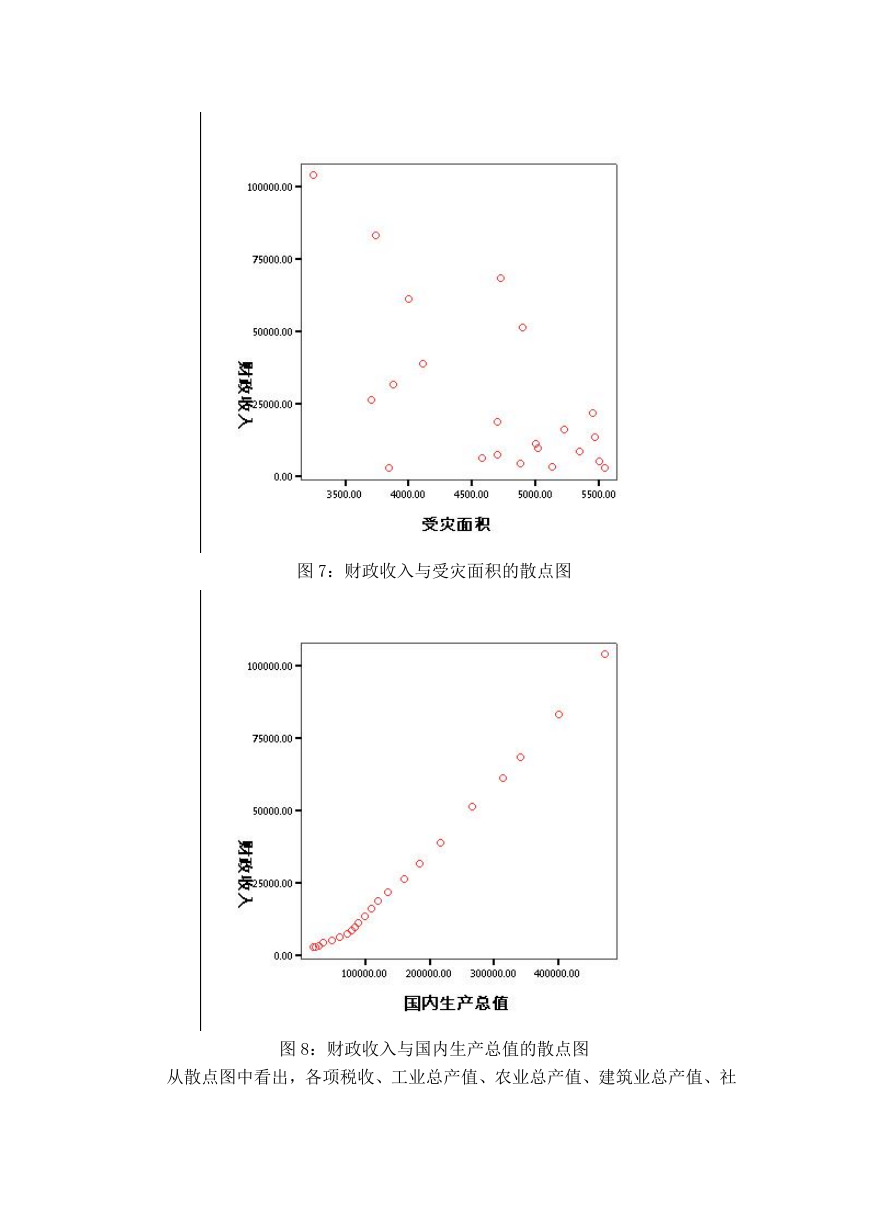
    首先通过 SPSS 软件构造以上数据的散点图，初步观察每个影响指标与就业 人数之间是否具有线性关系，如图 1 至图 8 所示。 图 1：财政收入与工业总产值的散点图
    图 2：财政收入与各项税收的散点图 图 3：财政收入与建筑业总产值的散点图 图 4：财政收入与农业总产值的散点图
    图 5：财政收入与人口数的散点图 图 6：财政收入与社会消费品零售总额的散点图
    图 7：财政收入与受灾面积的散点图 图 8：财政收入与国内生产总值的散点图 从散点图中看出，各项税收、工业总产值、农业总产值、建筑业总产值、社
    会消费品零售总额、国内生产总值这五个变量与财政收入基本呈线性分布；而人 口总数虽然也与财政收入存在正比的关系，但是从直观上看线性关系不显著，并 且人口因素呈现指数关系。受灾面积与财政收入总量的关系不明显。因此为使得 到的模型有显著的线性关系，在选取进入回归模型的自变量时，就要进行筛选。 故选择自变量为：各项税收、工业总产值、农业总产值、建筑业总产值、社会消 费品零售总额、国内生产总值。 2.2.2 模型建立 以国家财政收入为因变量，各项税收、工业总产值、农业总产值、建筑业总 产值、社会消费品零售总额、国内生产总值为自变量建立线性回归模型： 其中：y 为国家财政收入； y=β0+β1x1+β2x2+β3x3+β4x4+β5x5+β6x6+ε x1 为各项税收； x2 为工业总产值； x3 为农业总产值； x4 为建筑业总产值； x5 为社会消费品零售总额； x6 为国内生产总值； ε为随机误差项，β0 为常数项，βi 为待估计的参数； 为了便于模型的参数估计，对回归模型做如下基本假设： 假设 1：自变量是确定性变量，不是随机变量； 假设 2：随机误差项具有 0 均值和等方差； 假设 3：正态分布的假定条件为：εi~ N(0, σ2)，ε1，ε2，…，εn 相互独立。 2.2.3 数据生成及分析 本文使用运行软件 SPSS，利用逐步回归法对该问题进行分析。该方法从一 个自变量开始，视自变量对 y 的显著程度，从大到小地依次逐个引入回归方程， 但当引入的自变量由于后面的引入而变得不显著时，将其剔除。引入一个自变量 或从回归方程剔除一个自变量，为逐步回归的一步，对每一步都要进行 F 值检验， 以确保每次引入新的显著性自变量前回归方程中只包含对 y 作用显著的变量。这 个过程反复进行，直到既无不显著的变量从回归方程中剔除，又无显著变量可引 入为止。 本文通过对影响国家财政收入的 6 个指标进行逐步回归，步进方法标准选为 F 概率，进入为 0.050，移除为 0.100。 在第一次逐步回归分析中，用 SPSS 软件进行案例诊断，发现异常数据—— 第 21 行，即 2010 年数据，如图 9 所示。所以删除此行数据后再进行逐步回归分 析。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料