耿素云、屈婉玲、王捍贫版)离散课后答案.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：1.77M 资料格式：pdf 举报版权申诉

destinylord-3419936-4744302543357392725.pdf-第1页.png

第1页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第2页.png

第2页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第3页.png

第3页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第4页.png

第4页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第5页.png

第5页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第6页.png

第6页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第7页.png

第7页 / 共261页

destinylord-3419936-4744302543357392725.pdf-第8页.png

第8页 / 共261页

第一编集合论

第一章集合

习题 1.1

习题 1.2

习题 1.3

习题 1.4

习题 1.5

习题 1.6

习题 1.7

习题 1.8

习题 1.9

习题 1.10

习题 1.11

习题 1.12

习题 1.13

习题 1.14

习题 1.15

习题 1.16

习题 1.17

习题 1.18

习题 1.19

习题 1.20

习题 1.21

习题 1.22

习题 1.23

习题 1.24

习题 1.25

习题 1.26

习题 1.27

习题 1.28

习题 1.29

习题 1.30

习题 1.31

习题 1.32

习题 1.33

习题 1.34

习题 1.35

习题 1.36

第二章二元关系

习题 2.1

习题 2.2

习题 2.3

习题 2.4

习题 2.5

习题 2.6

习题 2.7

习题 2.8

习题 2.9

习题 2.10

习题 2.11

习题 2.12

习题 2.13

习题 2.14

习题 2.15

习题 2.16

习题 2.17

习题 2.18

习题 2.19

习题 2.20

习题 2.21

习题 2.22

习题 2.23

习题 2.24

习题 2.25

习题 2.26

习题 2.27

习题 2.28

习题 2.29

习题 2.30

习题 2.31

习题 2.32

习题 2.33

习题 2.34

习题 2.35

习题 2.36

习题 2.37

习题 2.38

习题 2.39

习题 2.40

习题 2.41

习题 2.42

习题 2.43

习题 2.44

习题 2.45

习题 2.46

习题 2.47

习题 2.48

习题 2.49

习题 2.50

习题 2.51

习题 2.52

习题 2.53

第三章函数

习题 3.1

习题 3.2

习题 3.3

习题 3.4

习题 3.5

习题 3.6

习题 3.7

习题 3.8

习题 3.9

习题 3.10

习题 3.11

习题 3.12

习题 3.13

习题 3.14

习题 3.15

习题 3.16

习题 3.17

习题 3.18

习题 3.19

习题 3.20

习题 3.21

习题 3.22

习题 3.23

习题 3.24

第四章自然数

习题 4.1

习题 4.2

习题 4.3

习题 4.4

习题 4.5

习题 4.6

习题 4.7

第五章基数（势）

习题 5.1

习题 5.2

习题 5.3

习题 5.4

习题 5.5

习题 5.6

习题 5.7

习题 5.8

习题 5.9

习题 5.10

习题 5.11

习题 5.12

习题 5.13

习题 5.14

第六章序数*

习题 6.1

习题 6.2

习题 6.3

习题 6.4

习题 6.5

习题 6.6

习题 6.7

习题 6.8

习题 6.9

习题 6.10

第二编图论

第七章图

习题 7.1

习题 7.2

习题 7.3

习题 7.4

习题 7.5

习题 7.6

习题 7.7

习题 7.8

习题 7.9

习题 7.10

习题 7.11

习题 7.12

习题 7.13

习题 7.14

习题 7.15

习题 7.16

习题 7.17

习题 7.18

习题 7.19

习题 7.20

习题 7.21

习题 7.22

习题 7.23

习题 7.24

习题 7.25

第八章欧拉图与哈密顿图

习题 8.1

习题 8.2

习题 8.3

习题 8.4

习题 8.5

习题 8.6

习题 8.7

习题 8.8

习题 8.9

习题 8.10

习题 8.11

习题 8.12

习题 8.13

习题 8.14

习题 8.15

习题 8.16

习题 8.17

第九章树

习题 9.1

习题 9.2

习题 9.3

习题 9.4

习题 9.5

习题 9.6

习题 9.7

习题 9.8

习题 9.9

习题 9.10

习题 9.11

习题 9.12

习题 9.13

习题 9.14

习题 9.15

习题 9.16

习题 9.17

习题 9.18

习题 9.19

习题 9.20

习题 9.21

第十章图的矩阵表示

习题 10.1

习题 10.2

习题 10.3

习题 10.4

习题 10.5

第十四章带权图及其应用

习题 14.1

习题 14.2

习题 14.3

习题 14.4

习题 14.5

习题 14.6

习题 14.7

习题 14.8

习题 14.9

习题 14.10

习题 14.11

习题 14.12

习题 14.13

第三编代数结构

第十五章代数系统

习题 15.1

习题 15.2

习题 15.3

习题 15.4

习题 15.5

习题 15.6

习题 15.7

习题 15.8

习题 15.9

习题 15.10

习题 15.11

习题 15.12

习题 15.13

习题 15.14

习题 15.15

习题 15.16

习题 15.17

习题 15.18

习题 15.19

习题 15.20

习题 15.21

习题 15.22

习题 15.23

习题 15.24

习题 15.25

习题 15.26

习题 15.27

习题 15.28

习题 15.29

习题 15.30

习题 15.31

习题 15.32

第十六章半群与独异点

习题 16.1

习题 16.2

习题 16.3

习题 16.4

习题 16.5

习题 16.6

习题 16.7

习题 16.8

习题 16.9

习题 16.10

习题 16.11

习题 16.12

习题 16.13

习题 16.14

习题 16.15

习题 16.16

第十七章群

习题 17.1

习题 17.2

习题 17.3

习题 17.4

习题 17.5

习题 17.6

习题 17.7

习题 17.8

习题 17.9

习题 17.10

习题 17.11

习题 17.12

习题 17.13

习题 17.14

习题 17.15

习题 17.16

习题 17.17

习题 17.18

习题 17.19

习题 17.20

习题 17.21

习题 17.22

习题 17.23

习题 17.24

习题 17.25

习题 17.26

习题 17.27

习题 17.28

习题 17.29

习题 17.30

习题 17.31

习题 17.32

习题 17.33

习题 17.34

习题 17.35

习题 17.36

习题 17.37

习题 17.38

习题 17.39

习题 17.40

习题 17.41

习题 17.42

习题 17.43

习题 17.44

习题 17.45

习题 17.46

习题 17.47

习题 17.48

习题 17.49

习题 17.50

习题 17.51

习题 17.52

习题 17.53

习题 17.54

习题 17.55

习题 17.56

习题 17.57

习题 17.58

习题 17.59

习题 17.60

习题 17.61

习题 17.62

习题 17.63

习题 17.64

习题 17.65

习题 17.66

习题 17.67

习题 17.68

习题 17.69

第十八章环与域

习题 18.1

习题 18.2

习题 18.3

习题 18.4

习题 18.5

习题 18.6

习题 18.7

习题 18.8

习题 18.9

习题 18.10

习题 18.11

习题 18.12

习题 18.13

习题 18.14

习题 18.15

习题 18.16

习题 18.17

习题 18.18

习题 18.19

习题 18.20

习题 18.21

习题 18.22

习题 18.23

习题 18.24

习题 18.25

习题 18.26

习题 18.27

习题 18.28

习题 18.29

习题 18.30

习题 18.31

习题 18.32

习题 18.33

习题 18.34

习题 18.35

习题 18.36

习题 18.37

习题 18.38

习题 18.39

习题 18.40

第十九章格与布尔代数

习题 19.1

习题 19.2

习题 19.3

习题 19.4

习题 19.5

习题 19.6

习题 19.7

习题 19.8

习题 19.9

习题 19.10

习题 19.11

习题 19.12

习题 19.13

习题 19.14

习题 19.15

习题 19.16

习题 19.17

习题 19.18

习题 19.19

习题 19.20

习题 19.21

习题 19.22

习题 19.23

习题 19.24

习题 19.25

习题 19.26

习题 19.27

习题 19.28

习题 19.29

习题 19.30

习题 19.31

习题 19.32

习题 19.33

习题 19.34

习题 19.35

习题 19.36

习题 19.37

习题 19.38

习题 19.39

习题 19.40

附录一北京大学计算机系考研真题解答(离散数学部分)

1990 年计算机数学基础

1991 年计算机数学基础

1992 年计算机数学基础

1993 年计算机数学基础

1994 年计算机数学基础

1995 年计算机数学基础

1996 年计算机数学基础

1997 年计算机数学基础

1998 年计算机数学基础

1999 年计算机数学基础

2000 年计算机数学基础

2001 年计算机数学基础

2002 年计算机数学基础

2003 年计算机专业基础

2004 年计算机专业基础

2005 年计算机数学基础

2006 年计算机数学基础

附录二教材定理汇总

第一章集合

定理 1.1

定理 1.2

定理 1.3

定理 1.4

定理 1.5

定理 1.6

第二章二元关系

定理 2.1

定理 2.2

定理 2.3

定理 2.4

定理 2.5

定理 2.6

定理 2.7

定理 2.8

定理 2.9

定理 2.10

定理 2.11

定理 2.12

定理 2.13

定理 2.14

定理 2.15

定理 2.16

定理 2.17

定理 2.18

定理 2.19

定理 2.20

定理 2.21

定理 2.22

定理 2.23

定理 2.24

定理 2.25

定理 2.26

定理 2.27

定理 2.28

定理 2.29

定理 2.30

定理 2.31

第三章函数

定理 3.1

定理 3.2

定理 3.3

定理 3.4

定理 3.5

定理 3.6

定理 3.7

定理 3.8

定理 3.9

定理 3.10

第四章自然数

定理 4.1

定理 4.2

定理 4.3

定理 4.4

定理 4.5

定理 4.6

定理 4.7

定理 4.8

定理 4.9

定理 4.10

定理 4.11

定理 4.12

定理 4.13

定理 4.14

定理 4.15

定理 4.16

定理 4.17

定理 4.18

定理 4.19

定理 4.20

定理 4.21

定理 4.22

定理 4.23

第五章基数(势)

定理 5.1

定理 5.2

定理 5.3

定理 5.4

定理 5.5

定理 5.6

定理 5.7

定理 5.8

定理 5.9

定理 5.10

定理 5.11

定理 5.12

定理 5.13

定理 5.14

定理 5.15

定理 5.16

定理 5.17

定理 5.18

定理 5.19

定理 5.20

定理 5.21

定理 5.22

定理 5.23

定理 5.24

定理 5.25

第六章序数*

定理 6.1

定理 6.2

定理 6.3

定理 6.4

定理 6.5

定理 6.6

定理 6.7

定理 6.8

定理 6.9

定理 6.10

定理 6.11

定理 6.12

定理 6.13

定理 6.14

定理 6.15

定理 6.16

定理 6.17

定理 6.18

定理 6.19

定理 6.20

定理 6.21

第七章图

定理 7.1

定理 7.2

定理 7.3

定理 7.4

定理 7.5

定理 7.6

定理 7.7

定理 7.8

定理 7.9

定理 7.10

定理 7.11

定理 7.12

定理 7.13

定理 7.14

定理 7.15

定理 7.16

定理 7.17

定理 7.18

定理 7.19

定理 7.20

定理 7.21

定理 7.22

第八章欧拉图与哈密顿图

定理 8.1

定理 8.2

定理 8.3

定理 8.4

定理 8.5

定理 8.6

定理 8.7

定理 8.8

定理 8.9

定理 8.10

定理 8.11

第九章树

定理 9.1

定理 9.2

定理 9.3

定理 9.4

定理 9.5

定理 9.6

定理 9.7

定理 9.8

定理 9.9

定理 9.10

定理 9.11

定理 9.12

定理 9.13

定理 9.14

定理 9.15

定理 9.16

定理 9.17

第十章图的矩阵表示

定理 10.1

定理 10.2

定理 10.3

定理 10.4

定理 10.5

第十一章平面图

定理 11.1

定理 11.2

定理 11.3

定理 11.4

定理 11.5

定理 11.6

定理 11.7

定理 11.8

定理 11.9

定理 11.10

定理 11.11

定理 11.12

定理 11.13

定理 11.14

定理 11.15

定理 11.16

定理 11.17

定理 11.18

定理 11.19

定理 11.20

定理 11.21

定理 11.22

定理 11.23

定理 11.24

第十二章图的着色

定理 12.1

定理 12.2

定理 12.3

定理 12.4

定理 12.5

定理 12.6

定理 12.7

定理 12.7'

定理 12.8

定理 12.9

定理 12.10

定理 12.11

定理 12.12

定理 12.13

定理 12.14

定理 12.15

定理 12.16

定理 12.17

第十三章支配集、覆盖集、独立集与匹配

定理 13.1

定理 13.2

定理 13.3

定理 13.4

定理 13.5

定理 13.6

定理 13.7

定理 13.8

定理 13.9

定理 13.10

定理 13.11

定理 13.12

定理 13.13

定理 13.14

第十四章带权图及其应用

定理 14.1

定理 14.2

定理 14.3

定理 14.4

定理 14.5

定理 14.6

定理 14.7

定理 14.8

定理 14.9

定理 14.10

定理 14.11

定理 14.12

定理 14.13

定理 14.14

定理 14.15

定理 14.16

定理 14.17

第十五章代数系统

定理 15.1

定理 15.2

定理 15.3

定理 15.4

定理 15.5

定理 15.6

定理 15.7

定理 15.8

定理 15.9

定理 15.10

定理 15.11

定理 15.12

第十六章半群与独异点

定理 16.1

定理 16.2

定理 16.3

定理 16.4

定理 16.5

定理 16.6

定理 16.7

定理 16.8

定理 16.9

定理 16.10

定理 16.11

第十七章群

定理 17.1

定理 17.2

定理 17.3

定理 17.4

定理 17.5

定理 17.6

定理 17.7

定理 17.8

定理 17.9

定理 17.10

定理 17.11

定理 17.12

定理 17.13

定理 17.14

定理 17.15

定理 17.16

定理 17.17

定理 17.18

定理 17.19

定理 17.20

定理 17.21

定理 17.22

定理 17.23

定理 17.24

定理 17.25

定理 17.26

定理 17.27

定理 17.28

定理 17.29

定理 17.30

定理 17.31

定理 17.32

定理 17.33

定理 17.34

定理 17.35

定理 17.36

定理 17.37

定理 17.38

定理 17.39

定理 17.40

定理 17.41

定理 17.42

定理 17.43

定理 17.44

第十八章环与域

定理 18.1

定理 18.2

定理 18.3

定理 18.4

定理 18.5

定理 18.6

定理 18.7

定理 18.8

定理 18.9

定理 18.10

定理 18.11

第十九章格与布尔代数

定理 19.1

定理 19.2

定理 19.3

定理 19.4

定理 19.5

定理 19.6

定理 19.7

定理 19.8

定理 19.9

定理 19.10

定理 19.11

定理 19.12

定理 19.13

定理 19.14

定理 19.15

定理 19.16

定理 19.17

定理 19.18

定理 19.19

定理 19.20

定理 19.21

定理 19.22

定理 19.23

定理 19.24

定理 19.25

定理 19.26

定理 19.27

定理 19.28

《离散数学教程》1 习题解答2 (beta 16 .11 )3 SOLVED AND TEXIFIED BY 肖新攀4 新版本下载、考研相关问题讨论请到计算机科学论坛—计算机考研交流版 (http://www.ieee.org.cn/list.asp?boardid=67) 1《离散数学教程》，耿素云、屈婉玲、王捍贫，北京大学出版社，2002年6月第1版，2003年1月第2次印刷 2此“习题解答”系个人作品，仅供学习交流之用，可以自由复制、打印和传播，但不得用作商业用途。如发现解答有错误，烦请告知作者(E-mail: xiaoxinpan@163.com)。 3版本号的整数部分表示该版本所包含答案的章数。发布日期： 2006 年 11 月 1 日。完成度(已完成题数/总题数)：60.17% 4由衷感谢 xbz 网友完成并制作本“习题解答”第十章和第十四章的全部内容、仔细检查其它各章节并提出众多修改意见和新的证明方法。感谢南京大学计算机系胡海星大侠长期以来给予我热情的鼓励和无私的帮助。感谢南京大学 02 计算机系赖江山同学提出各种建议和证明思路。感谢北京大学计算机系刘田教授给予我的帮助和鼓励。感谢 chouxiaoya、tedy、akaru、yitianxing、xuening、ourszf、ushing、pizzamx、 datoubaicai、echoqing、soup1122、lycool、hamletyj、leejunner、zliner、sunbird2002、zhaoming169、zqliu、 qiushuitian1111、tcschen、Supremgoooo、Smilingface、yangling 1985、jianzhentianxia、ouyangj0、kylinwang、赵现刚、熊亮等网友提出大量修改意见和新的证明方法。谢谢你们！

第一编集合论第一章集合第二章二元关系第三章函数第四章自然数第五章基数（势）第六章序数 ∗ 第二编图论第七章图第八章欧拉图与哈密顿图第九章树第十章图的矩阵表示第十四章带权图及其应用第三编代数结构第十五章代数系统目录 2 4 5 21 45 55 58 63 67 68 76 88 97 101 112 113

第十六章半群与独异点第十七章群第十八章环与域第十九章格与布尔代数附录一北京大学计算机系考研真题解答(离散数学部分) 附录二教材定理汇总 127 133 153 165 180 221 3

第一编集合论 4

第一章集合 1.1 (1) f2g； (2) f1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196g； (3) f1, 8, 27, 64g； (4) f0, 1, 2,¢¢¢g； (5) f2, 3g； (6) fa, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Zg。 1.2 (1) f(x, y) j x, y 2 R ^ x2 + y2 < 1g； (2) fθ j 9k(k 2 Z ^ θ = π 4 (3) fx j x 2 N ^ x < 8g； (4) f(x, y, z) j x, y, z 2 N ^ x2 + y2 = z2g； (5) fx j x 2 R ^ x2 + 5x + 6 = 0g。 + kπ)g； 1.3 (1), (4), (5), (6), (8), (9) 正确，其余不正确。 1.4 (1) 成立。证明: A 2 B ^ B C () A 2 B ^ 8x(x 2 B ! x 2 C) =) A 2 B ^ (A 2 B ! A 2 C) =) A 2 C (子集关系定义) (x/A) (假言推理) 2 (2) 不成立。举反例如下：令 A = fag, B = ffagg, C = ffag,fbgg，则有 A 2 B ^ B C，但 A * C。 (3) 不成立。举反例如下：令 A = fag, B = fa, bg, C = ffa, bg,fb, cgg，则有 A B ^ B 2 C，但 A /2 C。 (4) 不成立。举反例如下：令 A = fag, B = fa, bg, C = ffa, bg,fb, cgg，则有 A B ^ B 2 C，但 5

A * C。 1.5 令 A = fag, B = ffagg, C = fffaggg，则有 A 2 B ^ B 2 C，但 A /2 C。 1.6 (1) 0 元集：? 1 元集：fag,fbg,fcg 2 元集：fa, bg,fa, cg,fb, cg 3 元集：fa, b, cg 幂集：f?,fag,fbg,fcg,fa, bg,fa, cg,fb, cg,fa, b, cgg (2) 0 元集：? 1 元集：f1g,ff2, 3gg 2 元集：f1,f2, 3gg 幂集：f?,f1g,ff2, 3gg,f1,f2, 3ggg (3) 0 元集：? 1 元集：f?g,ff?gg 2 元集：f?,f?gg 幂集：f?,f?g,ff?gg,f?,f?ggg (4) 0 元集：? 1 元集：ff1, 2gg 幂集：f?,ff1, 2ggg (5) 0 元集：? 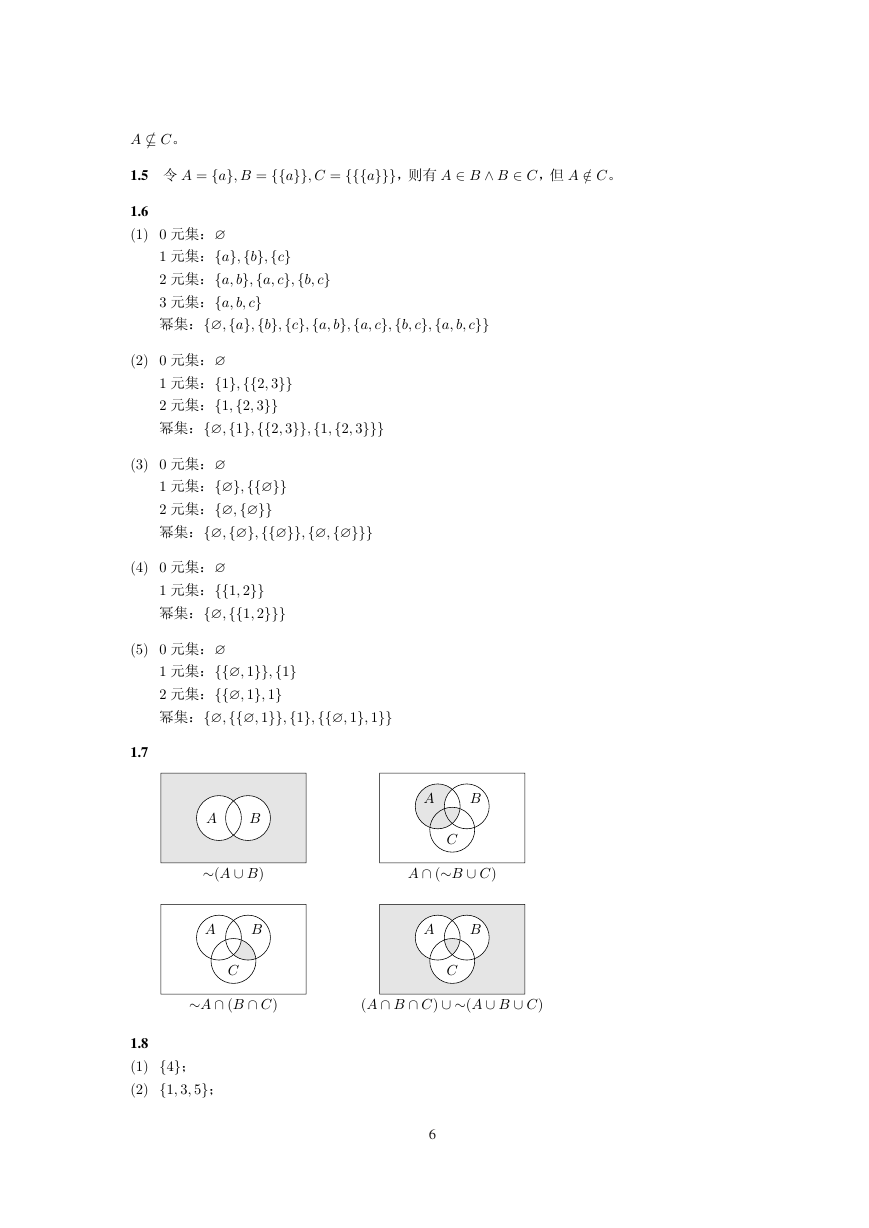1 元集：ff?, 1gg,f1g 2 元集：ff?, 1g, 1g 幂集：f?,ff?, 1gg,f1g,ff?, 1g, 1gg 1.7 1.8 (1) f4g； (2) f1, 3, 5g； 6 AB»(A[B)ABCA\(»B[C)ABC»A\(B\C)ABC(A\B\C)[»(A[B[C)

(3) f2, 3, 4, 5g； (4) f2, 3, 4, 5g； (5) f?,f4gg； (6) ff1g,f1, 4gg。 1.9 (1) f¡7,¡6,¡5,¡4,¡3,¡2,¡1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 15, 16, 18, 21, 24, 27, 30, 32, 64g； (2) ?； (3) f¡7,¡6,¡5,¡4,¡3,¡2,¡1, 4, 5g； (4) f¡7,¡6,¡5,¡4,¡3,¡2,¡1, 0, 3, 4, 5, 6, 9, 12, 15, 18, 21, 24, 27, 30g。 1.10 因为 P(A) = f?,fagg，PP(A) = f?,f?g,ffagg,f?,faggg，故 (1), (2), (4), (5) 成立，其余不成立。 1.11 证明: 必要性：若 A ¡ B = A，则有： A \ B = (A ¡ B) \ B = (A \ »B) \ B = A \ (»B \ B) = A \ ? = ? 充分性：若 A \ B = ?，则有： A = A \ E = A \ (B [ »B) = (A \ B) [ (A \ »B) = ? [ (A \ »B) = A \ »B = A ¡ B 综合得：A ¡ B = A , A \ B = ?。 1.12 先证一个引理：引理 1.1 对任意集合 A 和 B，有 A ¡ B = ? , A B。证明: A ¡ B = ? () :9x(x 2 (A ¡ B)) () 8x:(x 2 (A ¡ B)) () 8x:(x 2 A ^ x /2 B) () 8x:(x 2 A ^ :x 2 B) () 8x(:x 2 A _ x 2 B) () 8x(x 2 A ! x 2 B) () A B 7 (A ¡ B = A) (补交转换律) (结合律) (矛盾律) (零律) (同一律) (排中律) (分配律) (A \ B = ?) (同一律) (补交转换律) 2 (? 定义) (量词否定等值式) (相对补定义) ( /2 定义) (命题逻辑德¢摩根律) (蕴涵等值式) (子集关系定义)

(1) 答：(A ¡ B) [ (A ¡ C) = A 当且仅当 A \ B \ C = ? 。证明: (A ¡ B) [ (A ¡ C) = A () A ¡ (B \ C) = A () A \ (B \ C) = ? () A \ B \ C = ? (2) 答：(A ¡ B) [ (A ¡ C) = ? 当且仅当 A (B \ C)。证明: (A ¡ B) [ (A ¡ C) = ? () A ¡ (B \ C) = ? () A (B \ C) (3) 答：(A ¡ B) \ (A ¡ C) = ? 当且仅当 A (B [ C)。证明: (A ¡ B) \ (A ¡ C) = ? () A ¡ (B [ C) = ? () A (B [ C) (4) 答：(A ¡ B) \ (A ¡ C) = A 当且仅当 A \ (B [ C) = ?。证明: (A ¡ B) \ (A ¡ C) = A () A ¡ (B [ C) = A () A \ (B [ C) = ? 1.13 (1) 先证两个引理：引理 1.2 对任意集合 A 和 B，有： A \ B A 和 A \ B B。证明: 8x， x 2 A \ B () x 2 A ^ x 2 B =) x 2 A 故有，A \ B A。同理可证：A \ B B。引理 1.3 对任意集合 A 和 B，有： A A [ B 和 B A [ B 证明: 8x， x 2 A =) x 2 A _ x 2 B () x 2 A [ B 故有，A A [ B。同理可证：B A [ B。再证原题：证明: (A ¡ B) ¡ C = (A \ »B) \ »C A \ »B 8 2 (德¢摩根律) (习题 1.11 结论) (结合律) 2 (德¢摩根律) (引理 1.1) 2 (德¢摩根律) (引理 1.1) 2 (德¢摩根律) (习题 1.11 结论) 2 (集合交定义) (命题逻辑化简律) 2 (命题逻辑附加律) (集合并定义) 2 (补交转换律) (引理 1.2)

分享到：

赞收藏

资料库

耿素云、屈婉玲、王捍贫版)离散课后答案.pdf

相关推荐

课程资源

热门标签

最新资料