logo资料库

数据结构课程设计报告书.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.13M 资料格式：doc 举报 版权申诉
第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
资料共16页，剩余部分请下载后查看
    武汉理工大学《数据结构》课程设计说明书 目录 一． 问题分析和任务定义 …………………………3 1.分析 2.测试数据 <1>.用于正确性检测的合法数据 <2>.用于健壮性检测的非法输入数据 二． 开发平台 ……………………………………4 三． 数据类型和系统设计 ………………………4 1.逻辑设计 2.详细设计 <1>.图的初始化 <2>.构造图 <3>.克鲁斯卡尔算法的实现 <4>.输出邻接矩阵 <5>.主函数的实现 四． 程序调试与运行结果分析 ………………10 1.程序调试 2.运行结果 五． 自我评价与总结 ……………………………11 …………………………………12 六． 参考文献 1
    武汉理工大学《数据结构》课程设计说明书 课程设计任务书 学生姓名： 齐雪婷 专业班级： 计算机 0801 指导教师： 杨克俭 工作单位： 计算机科学系 题 目: 最小生成树问题 若要在 n 个城市之间建设通信网络，只需要架设 n-1条线路即可。如何以最低的经济 代价建设这个通信网，是一个网的最小生成树问题。 （1）利用克鲁斯卡尔算法求网的最小生成树。 （2）实现教科书 6.5 节中定义的抽象树类型 MFSet。以此表示构造生成树过程中的连 通分量。 （3）以文本形式输出生成树中各条边以及他们的权值。 （4）测试用例见严蔚敏《数据结构习题集(C 语言版)》p152。 要求完成的主要任务: （包括课程设计工作量及其技术要求，以及说明书撰写 等具体要求） 课程设计报告按学校规定格式用 A4 纸打印（书写），并应包含如下内容： 1. 问题描述 简述题目要解决的问题是什么。 2. 设计 存储结构设计、主要算法设计（用类 C/C++语言或用框图描述）、测试用例设计； 3. 调试报告 调试过程中遇到的问题是如何解决的；对设计和编码的讨论和分析。 4. 经验和体会（包括对算法改进的设想） 5. 附源程序清单和运行结果。源程序要加注释。如果题目规定了测试数据，则运行结 果要包含这些测试数据和运行输出。 说明： 1. 设计报告、程序不得相互抄袭和拷贝；若有雷同，则所有雷同者成绩均为 0 分。 2. 凡拷贝往届任务书或课程设计充数者，成绩一律无效，以 0 分记。 时间安排： 1、第 18 周完成。 2、7 月 2 日 8:30 时到实验中心检查程序、交课程设计报告、源程序（U 盘）。 指导教师签名： 2010 年 6 月 22 日 系主任（或责任教师）签名： 年 月 日 2
    武汉理工大学《数据结构》课程设计说明书 一． 问题分析和任务定义 1.分析 <1>.在 n 个城市间建设通信网络，要求以最小的成本，即是求图的最小生成 树。该课程设计中求最小生成树要求使用克鲁斯卡尔算法。所编的程序应先按输 入建立图，再根据求最小生树的方法求出最小生成树。输入的顶点可以是字符串 也可以是数字(此时将数字当作是字符存入)，输入的权值为整数。输入前输出提 示，提示如何输入。输出图所对应的邻接矩阵，根据所输入的根构造出最小生成 树，最小生成树输出形式为：顶点权值顶点。 <2>.本程序的目的是要建设一个最经济的通信网，根据用户指定的始点和终 点 输出相应的路径，以及两点之间的距离。在这里城市以及两城市之间的距离 都要整型数来代替。 <3>．程序执行的命令包括： a）利用克鲁斯卡尔算法求最小生成树。 b）构造最小生成树中的连通分量。 c）输入顶点个数。 d）求出两顶点之间的最小权值边。 2.测试数据 <1>.用于正确性检测的合法数据 a) 以北京、天津、上海、重庆作为顶点，以北京 45 天津、天津 90 上海、 上海 60 重庆、重庆 80 北京、上海 85 天津为孤作为测试数据；并且以 北京为树根进行测试。 b) 以 1 2 3 4 作为顶点，以 1 3 2，1 9 3，1 12 4，2 15 3，3 2 4，为孤作为 测试数据；并以 A 为树根进行测试。 3
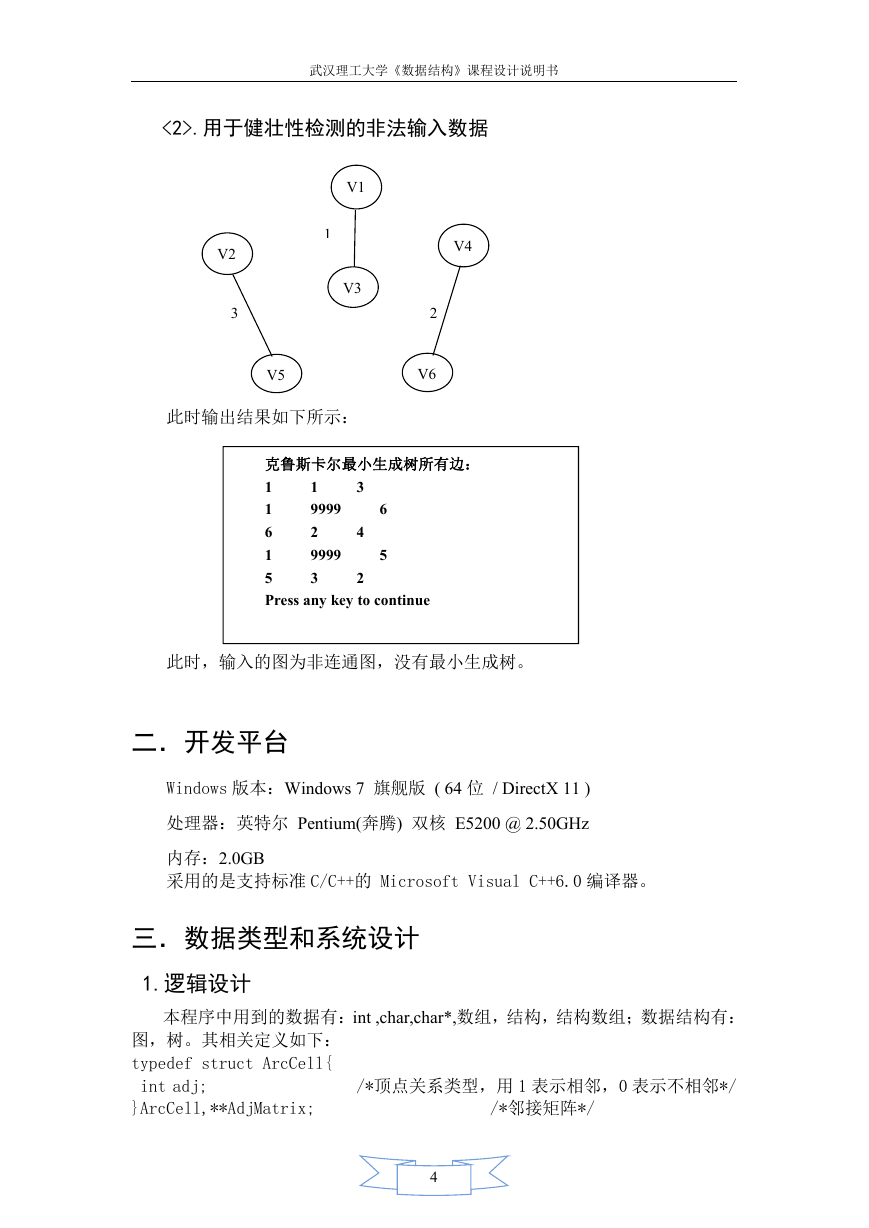
    武汉理工大学《数据结构》课程设计说明书 <2>.用于健壮性检测的非法输入数据 1 V1 V3 V2 3 V5 V4 2 V6 此时输出结果如下所示： 6 克鲁斯卡尔最小生成树所有边： 1 1 6 1 5 Press any key to continue 1 9999 2 9999 3 5 3 4 2 此时，输入的图为非连通图，没有最小生成树。 二．开发平台 Windows 版本：Windows 7 旗舰版 ( 64 位 / DirectX 11 ) 处理器：英特尔 Pentium(奔腾) 双核 E5200 @ 2.50GHz 内存：2.0GB 采用的是支持标准 C/C++的 Microsoft Visual C++6.0 编译器。 三．数据类型和系统设计 1.逻辑设计 本程序中用到的数据有：int ,char,char*,数组，结构，结构数组；数据结构有： 图，树。其相关定义如下： typedef struct ArcCell{ int adj; /*顶点关系类型，用 1 表示相邻，0 表示不相邻*/ }ArcCell,**AdjMatrix; /*邻接矩阵*/ 4
    武汉理工大学《数据结构》课程设计说明书 /*顶点值*/ /*顶点向量*/ /*邻接矩阵*/ /*图的顶点数和边数*/ typedef struct type{ char data[3]; }VertexType; typedef struct{ VertexType *vexs; AdjMatrix arcs; int vexnum,arcnum; }MGraph; struct clos{ VertexType adjvex; int lowcost; }*closedge; void InitGraph(MGraph *G) { ……………………………………………………… } /*初始图*/ void CreateUND(MGraph *G) { ……………………………………………………… } /*采用数组（邻接矩阵）*/ Void MiniSpanTree(MGraph G,VertexType u) /*从第 U 个顶点出发构造最小生成树，输出各条边*/ { ……………………………………………………… } void Pint(MGraph G) /*输出邻接矩阵*/ { ……………………………………………………….. } void main() /*主函数模板*/ { ……………………………………………………….. } 5
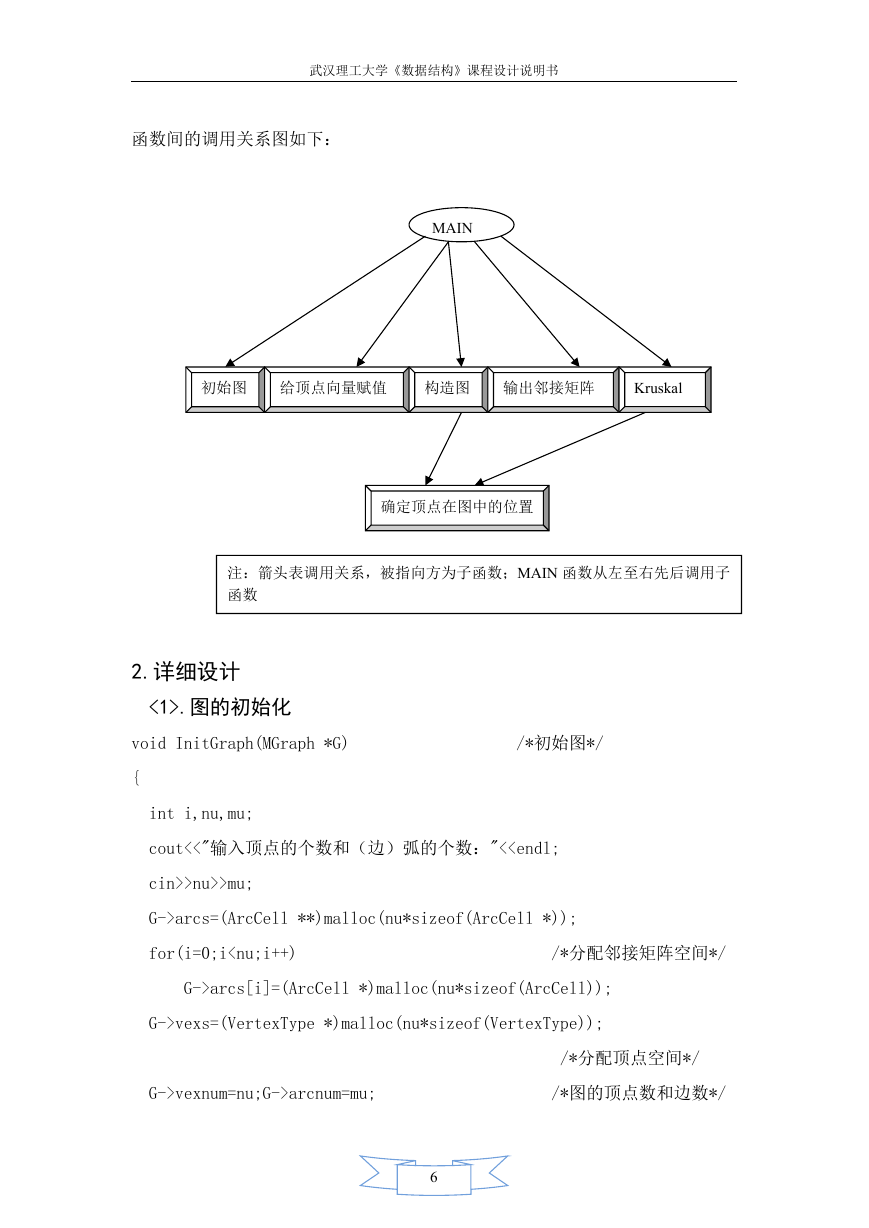
    武汉理工大学《数据结构》课程设计说明书 函数间的调用关系图如下： MAIN 初始图 给顶点向量赋值 构造图 输出邻接矩阵 Kruskal 确定顶点在图中的位置 注：箭头表调用关系，被指向方为子函数；MAIN 函数从左至右先后调用子 函数 2.详细设计 <1>.图的初始化 void InitGraph(MGraph *G) /*初始图*/ { int i,nu,mu; cout<<"输入顶点的个数和（边）弧的个数："<>nu>>mu; G->arcs=(ArcCell **)malloc(nu*sizeof(ArcCell *)); for(i=0;iarcs[i]=(ArcCell *)malloc(nu*sizeof(ArcCell)); G->vexs=(VertexType *)malloc(nu*sizeof(VertexType)); G->vexnum=nu;G->arcnum=mu; /*图的顶点数和边数*/ /*分配顶点空间*/ 6
    武汉理工大学《数据结构》课程设计说明书 } <2>.构造图 该设计中采用邻接矩阵来构造图 void CreateUND(MGraph *G) { int i,j,k,*p , w; VertexType v1,v2; p=(int *)malloc(G->vexnum*sizeof(int)); for(i=0;i<10;i++) p[i]=0; for(i=0;ivexnum;i++) /*初始邻接表*/ { for(j=0;jvexnum;j++) G->arcs[i][j].adj=ING;} cout<<"按顺序输入顶点和它们的权值再顶点： "<arcnum;k++) cout<<"输入第" <>v1.data>>w>>v2.data; /*输入相邻的两个点值和权值*/ i=Locate(*G,v1);j=Locate(*G,v2); /*用 i 和 j 来确定它们的位置*/ G->arcs[i][j].adj=w; G->arcs[j][i].adj=G->arcs[i][j].adj; /*有向图时就不用这个*/ { } } <3>.克鲁斯卡尔算法的实现 假设连通网 N=（V,{E}）,则令最小生成树的初始状态为只有 n 个顶点而无 边的非连通图 T=（V,{}）,图中每个顶点自成一个连通分量。在 E 中选择代价最 小的边，若该边依附的顶点落在 T 中不同的连通分量上，则将此边加入到 T 中， 否则舍去此边而选择下一条代价最小的边。依次类推，直至 T 中所有顶点都在同 一连通分量上为止。 Void MiniSpanTree(MGraph G,VertexType u) /*从第 U 个顶点出发构造最小生成树，输出各条边*/ 7
    武汉理工大学《数据结构》课程设计说明书 { int k,j,i; closedge=(struct clos *)malloc(G.vexnum*sizeof(struct clos)); /*为数组分配空间*/ k=Locate(G,u); /*U 的位置*/ for(j=0;j.输出邻接矩阵 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料