有限元分析教程（英文）.pdf-资料库

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第1页.png

第1页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第2页.png

第2页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第3页.png

第3页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第4页.png

第4页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第5页.png

第5页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第6页.png

第6页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第7页.png

第7页 / 共309页

1ddcf408-99b6-49ce-ac47-b342aae15133.pdf-第8页.png

第8页 / 共309页

有限元分析有限元分析段少东整理

1 Module 1: Introduction to Finite Element Analysis Lecture 1: Introduction 1.1.1 Introduction The Finite Element Method (FEM) is a numerical technique to find approximate solutions of partial differential equations. It was originated from the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. In a structural simulation, FEM helps in producing stiffness and strength visualizations. It also helps to minimize materialweight and its cost of the structures. FEM allows for detailed visualization and indicates the distribution of stresses and strains inside the body of a structure. Many of FE software are powerful yet complex tool meant for professional engineers with the training and education necessary to properly interpret the results. Several modern FEM packages include specific components such as fluid, thermal, electromagnetic and structural working environments. FEM allows entire designs to be constructed, refined and optimized before the design is manufactured. This powerful design tool has significantly improved both the standard of engineering designs and the methodology of the design process in many industrial applications. The use of FEM has significantly decreased the time to take products from concept to the production line. One must take the advantage of the advent of faster generation of personal computers for the analysis and design of engineering product with precision level of accuracy. 1.1.2 Background of Finite Element Analysis The finite element analysis can be traced back to the work by Alexander Hrennikoff (1941)and Richard Courant(1942). Hrenikoff introduced the framework method, in which a plane elastic medium was represented as collections of bars and beams.These pioneers share one essential characteristic: mesh discretization of a continuous domain into a set of discrete sub-domains, usually called elements. • • • • • In 1950s, solution of large number of simultaneous equations became possible because of the digitalcomputer. In 1960, Ray W. Clough first published a paper using term “Finite Element Method”. In 1965, First conference on “finite elements” was held. In 1967, the first book on the “Finite Element Method” was published by Zienkiewicz and Chung. In the late 1960s and early 1970s, the FEM was applied to a wide variety of engineering problems. IIT Kharagpur NPTEL Web Course - 1 -

2 • • In the 1970s, most commercial FEM software packages (ABAQUS, NASTRAN, ANSYS, etc.) originated.Interactive FE programs on supercomputer lead to rapid growth of CAD systems. In the 1980s, algorithm on electromagnetic applications, fluid flow and thermal analysis were developed with the use of FE program. • Engineers can evaluate ways to control the vibrations and extend the use of flexible, deployablestructures in space using FE and other methods in the 1990s. Trends to solve fully coupled solution of fluid flows with structural interactions, bio-mechanics related problems with a higher level of accuracy were observed in this decade. With the development of finite element method, together with tremendous increases in computing power and convenience, today it is possible to understand structural behavior with levels of accuracy. This was in fact the beyond of imagination before the computer age. 1.1.3 Numerical Methods The formulation for structural analysis is generally based on the three fundamental relations: equilibrium, constitutive and compatibility. There are two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. However, in reality, such simple cases may not arise. As a result, various numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these relations are only approximately satisfied. The numerical method depends heavily on the processing power of computers and is more applicable to structures of arbitrary size and complexity. It is common practice to use approximate solutions of differential equations as the basis for structural analysis. This is usually done using numerical approximation techniques. Few numerical methods which are commonly used to solve solid and fluid mechanics problems are given below. • Finite Difference Method • Finite Volume Method • Finite Element Method • Boundary Element Method • Meshless Method The application of finite difference method for engineering problems involves replacing the governing differential equations and the boundary condition by suitable algebraic equations. For IIT Kharagpur NPTEL Web Course - 2 -

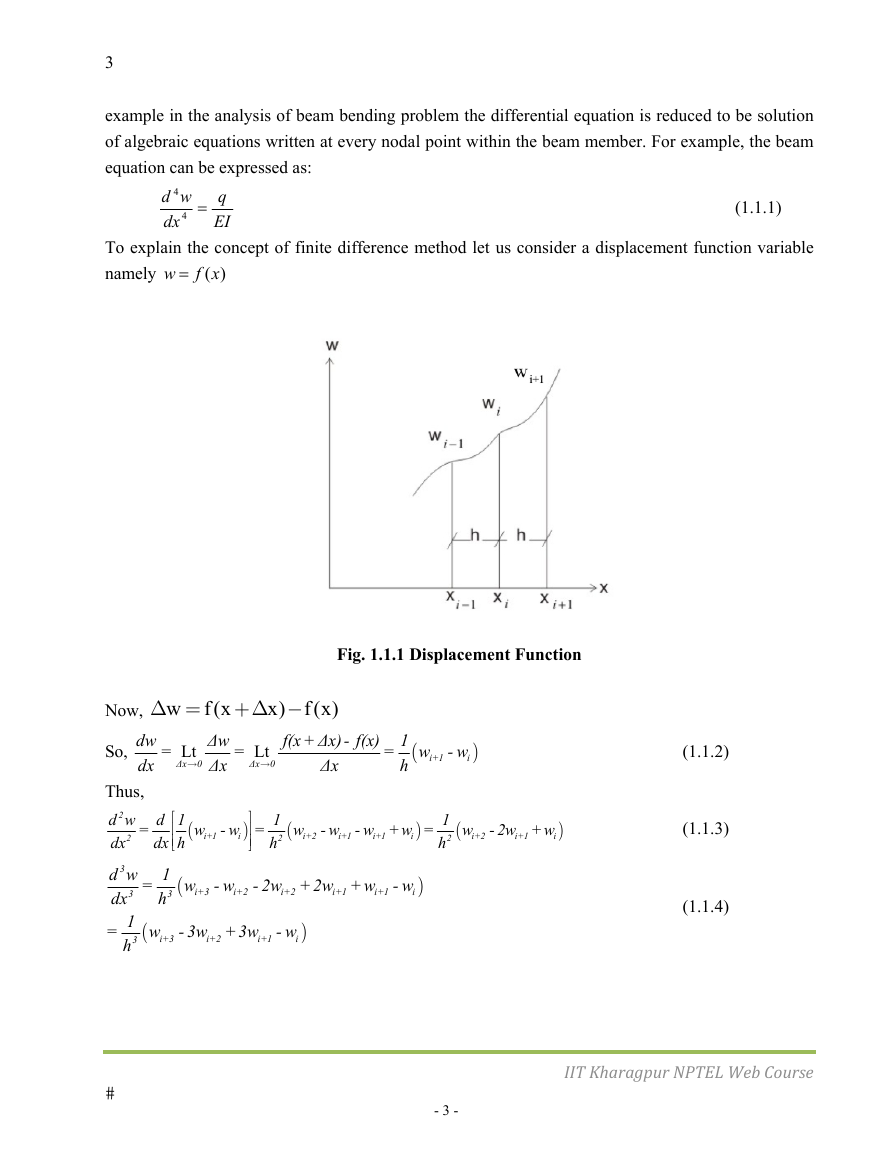
3 example in the analysis of beam bending problem the differential equation is reduced to be solution of algebraic equations written at every nodal point within the beam member. For example, the beam equation can be expressed as: wd 4 dx =4 q EI (1.1.1) To explain the concept of finite difference method let us consider a displacement function variable namely w f x ( ) = Fig. 1.1.1 Displacement Function +Δ − x) f(x) f(x+ Δx)- f(x) Δx = 1 h ( w - w i+1 i ) 0 0 = = So, Lt → Δx Lt → Δx Δ = Now, w f (x Δw Δx dw dx Thus, ⎡ d w d 1 2 ⎢ ⎢ dx h dx ⎣ 1= d w 3 h dx 3 1= w - 3w +3w - w i+3 i h w - w = i+1 1 h 2 ⎤ ) ⎥ ⎥ ⎦ = i+2 ( 3 ( 3 2 ) i+1 ( i ( ) w - w - w +w = i+2 i+1 i+1 i w - w - 2w + 2w + w - w i+3 i i+2 i+2 i+1 i+1 1 h 2 ( w - 2w +w i+2 i i+1 ) ) (1.1.2) (1.1.3) (1.1.4) IIT Kharagpur NPTEL Web Course - 3 -

4 ( 4 w - w - 3w +3w +3w - 3w - w + w i+4 i i+2 i+2 i+3 i+3 i+1 i+1 i+3 1= h w - 4w +6w - 4w + w i+4 i d w 4 dx 4 1= h 1= h Thus, eq. (1.1.1) can be expressed with the help of eq. (1.1.5) and can be written in finite difference form as: w - 4w +6w - 4w +w i+2 i-2 (1.1.5) i+2 i+1 i+1 ( ( 4 4 i i-1 ) ) ) ( w i − 2 − 4 w i 1 − + 6 w i − 4 w i 1 + + w i + 2 ) = q EI 4 h (1.1.6) Fig. 1.1.2 Finite difference equation at node i Thus, the displacement at node i of the beam member corresponds to uniformly distributed load can be obtained from eq. (1.1.6) with the help of boundary conditions. It may be interesting to note that, the concept of node is used in the finite difference method. Basically, this method has an array of grid points and is a point wise approximation, whereas, finite element method has an array of small interconnecting sub-regions and is a piece wise approximation. Each method has noteworthy advantages as well as limitations. However it is possible to solve various problems by finite element method, even with highly complex geometry and loading conditions, with the restriction that there is always some numerical errors. Therefore, effective and reliable use of this method requires a solid understanding of its limitations. 1.1.4 Concepts of Elements and Nodes Any continuum/domain can be divided into a number of pieces with very small dimensions. These small pieces of finite dimension are called ‘Finite Elements’ (Fig. 1.1.3). A field quantity in each element is allowed to have a simple spatial variation which can be described by polynomial terms. Thus the original domain is considered as an assemblage of number of such small elements. These elements are connected through number of joints which are called ‘Nodes’. While discretizing the structural system, it is assumed that the elements are attached to the adjacent elements only at the nodal points. Each element contains the material and geometrical properties. The material properties inside an element are assumed to be constant. The elements may be 1D elements, 2D elements or 3D elements. The physical object can be modeled by choosing appropriate element such as frame IIT Kharagpur NPTEL Web Course - 4 -

5 element, plate element, shell element, solid element, etc. All elements are then assembled to obtain the solution of the entire domain/structure under certain loading conditions. Nodes are assigned at a certain density throughout the continuum depending on the anticipated stress levels of a particular domain. Regions which will receive large amounts of stress variation usually have a higher node density than those which experience little or no stress. Fig. 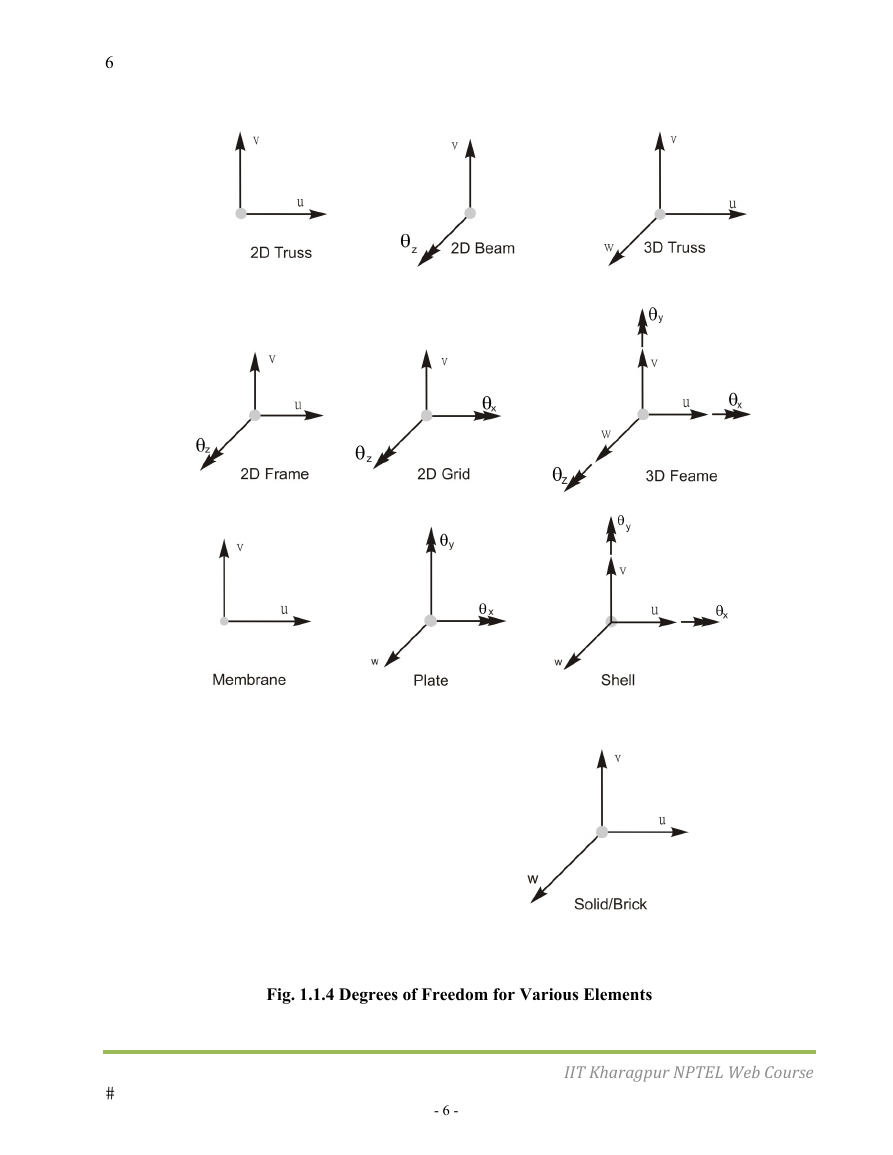1.1.3 Finite element discretization of a domain 1.1.5 Degrees of Freedom A structure can have infinite number of displacements. Approximation with a reasonable level of accuracy can be achieved by assuming a limited number of displacements. This finite number of displacements is the number of degrees of freedom of the structure. For example, the truss member will undergo only axial deformation. Therefore, the degrees of freedom of a truss member with respect to its own coordinate system will be one at each node. If a two dimension structure is modeled by truss elements, then the deformation with respect to structural coordinate system will be two and therefore degrees of freedom will also become two. The degrees of freedom for various ) types of element are shown in Fig. 1.1.4 for easy understanding. Here ( θ θ θ represent displacement and rotation respectively. ,u v w and ( , ) , x , y z IIT Kharagpur NPTEL Web Course - 5 -

6 Fig. 1.1.4 Degrees of Freedom for Various Elements IIT Kharagpur NPTEL Web Course - 6 -

7 Module 1: Introduction to Finite Element Analysis Lecture 2: Basic Concepts of Finite Element Analysis 1.2.1 Idealization of a Continuum A continuum may be discretized in different ways depending upon the geometrical configuration of the domain. Fig. 1.2.1 shows the various ways of idealizing a continuum based on the geometry. Fig. 1.2.1 Various ways of Idealization of a Continuum 1.2.2 Discretization of Technique The need of finite element analysis arises when the structural system in terms of its either geometry, material properties, boundary conditions or loadings is complex in nature. For such case, the whole IIT Kharagpur NPTEL Web Course - 7 -

资料库

有限元分析教程（英文）.pdf

相关推荐

课程资源

热门标签

最新资料