PSO算法PID整定.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：1.11M 资料格式：pdf 举报版权申诉

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第1页.png

第1页 / 共6页

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第2页.png

第2页 / 共6页

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第3页.png

第3页 / 共6页

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第4页.png

第4页 / 共6页

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第5页.png

第5页 / 共6页

e709cc1b-c9c4-44ac-a21f-5f39c91d3bff.pdf-第6页.png

第6页 / 共6页

文本预览

Journal of Computer Applications 计算机应用，2019，39( 3) : 796 － 801 ISSN 1001-9081 CODEN JYIIDU 2019-03-10 http: / / www． joca． cn 文章编号: 1001-9081 ( ) 2019 03-0796-06 : DOI 10． 11772 / j． issn． 1001-9081． 2018081698 改进的粒子群优化算法优化分数阶 PID 控制器参数金滔 * ，董秀成，李亦宁，任磊，范佩佩西华大学信号与信息处理重点实验室成都， 610039) ( 通信作者电子邮箱 ( * 994357660@ qq． com) 摘要: 为了提高分数阶比例积分微分( FOPID) 控制器的控制效果，针对 FOPID 控制器参数整定的范围广、复杂性高等特点，提出改进的粒子群优化( PSO) 算法优化 FOPID 控制器参数的方法。该算法对 PSO 中惯权重系数的上下限设定范围并随迭代次数以伽玛函数方式非线性下降，同时粒子的惯性权重系数和学习因子根据粒子的适应度值大小动态调整，使粒子保持合理运动惯性和学习能力，提高粒子的自适应能力。仿真实验表明，改进的 PSO 算法优化 FOPID 控制器的参数较标准 PSO 算法具有收敛速度快和收敛精度高等优点，使 FOPID 控制器得到较优的综合性能。关键词: 分数阶比例积分微分控制器; 粒子群优化; 惯性权重系数; 参数优化; 自适应中图分类号: 文献标志码: TP273 A Optimization of fractional PID controller parameters based on improved PSO algorithm JIN Tao * ， DONG Xiucheng， LI Yining，ＲEN Lei， FAN Peipei ( Signal and Information Processing Key Laboratory， Xihua University， Chengdu Sichuan 610039， China) Abstract: Aiming at poor control effect of Fractional Order Proportional-Integral-Derivative ( FOPID) controller and the characteristics of wide range and high complexity of parameter tuning for FOPID controller， an improved Particle Swarm Optimization ( PSO) method was proposed to optimize the parameters of FOPID controller． In the proposed algorithm， the upper and lower limits of inertial weight coefficients in PSO were defined and decreased nonlinearly with the iteration times in form of Gamma function， meanwhile， the inertia weight coefficients and learning factors of particles were dynamically adjusted according to the fitness value of particles， making the particles keep reasonable motion inertia and learning ability， and improving self-adaptive ability of the particles． Simulation experiments show that the improved PSO algorithm has faster convergence rate and higher convergence accuracy than the standard PSO algorithm in optimizing the parameters of FOPID controller， which makes the FOPID controller obtain better comprehensive performance． Key words: Fractional Order PID ( FOPID) controller; Particle Swarm Optimization ( PSO) ; inertial weight coefficient; parameter optimization; self-adaption 0 引言分数阶比例积分微分 ( ， FOPID 与传统的［ 1 Podlubny ) 控制器首先由 Proportional-Integral-Derivative ， Integral-Derivative 传统比例积分微分( 器使用分数演算的一种推广 Fractional Order Proportional- ］提出，是 ) 控制控制器相比，控制器中积分次数和微分次数不是整数，控制器参数 FOPID 的维度和范围变大，为实现复杂的控制性能提供更大的灵活分数阶控制算法中附加的积分阶和微分阶数为提高系统性的鲁棒性在控制领域， PID 因此，研究稳定性和暂态性能提供了更多的可能性、控制无疑是工业应用中应用最广泛的控制算法 PID PID 。。。。控制器具有重要的现实意义控制相比，。与传统的程领域的理论和应用研究显示出了许多优点加两个附加的参数，使得 FOPID 控制器在许多科学和工然而，由于增控制器的参数整定变得更加。 PID FOPID FOPID 。 FOPID 参数整定的方法有优化方法目前幅度裕量与相位裕量法［、主导极点复杂随着智能优化算法的兴起法［］ 2 和广泛应用以及计算机技术的快速发展，越来越多的优化方法应用在参数整定中李新波等［］使用、。］ 3 ( 4 FOPID 。 ) 神经网络建模得到的ＲBF Ｒadial 信息来整定 Basis Function Jacobain 控制器中的参数并应用在压电叠堆控制中。Zhang 控制器参数整定问题转化为一个非凸优化问 FOPID 等［］将题，引入一种新的元启发式方法 FOPID 5 状态转移算法 ( ， STA ——— ) 来选择最优的 State 控制器参数。 FOPID Transition Algorithm 张欣等［ 6 ］采用量子粒子群 ( ) 优化算法优化 Quantum Particle Swarm 控制器参数，融合 Optimization 了量子计算的方法和粒子群算法的思想，使得算法具有更强的全局寻优能力，克服了粒子群算法早熟收敛的缺点 FOPID QPSO ，。］在粒子群优化算法的原速度更新公式中加入自适［ 7 Aghababa 应加速器参数，提高优化 FOPID 控制器参数的速度。Das ) ; 四川省高校科研创新团队项目 ( 18TD0024 ) ; 四威高科 — 西华大学产学研联合实验室收稿日期: 基金项目: 四川省科技厅重点项目( ; 修回日期: 2018-08-16 2018-09-26 2018-10-18。 ; 录用日期: ) ; 西华大学研究生创新基金资助项目( 2018JY0463 ycjj2018073 。 ) ( 2016-YF04-00044-JH 作者简介: 金滔( 1992— 士，主要研究方向: 智能控制四川成都人，硕士研究生，主要研究方向: 数字图像处理; 范佩佩( ) ，男，四川合江人，硕士研究生，主要研究方向: 智能算法机器人控制; 李亦宁( 、 1995— ) ，男，四川乐山人，硕士研究生，主要研究方向: 机器人控制; 任磊( ) ，女，重庆渝北人，硕士研究生，主要研究方向: 机器视觉智能控制; 董秀成( 、 ) ，男，四川成都人，教授，硕 ) ，男， 1963— 1995— 1994— 。

第 3 期金滔等: 改进的粒子群优化算法优化分数阶 PID 控制器参数 797 3 μ λ 和积分阶次个参数增加到，使得控制器的可调参数由数: 微分阶次 PID 控制器的控制器参。数维度的增加，控制参数可调范围更广，控制模型更为精确，对被控对象的控制更加地灵活方便，从而使被控对象可获得更好的动态和静态特性，以满足复杂系统的各项性能指标微分系数控制的个参数 FOPID 。 5 ki 、 kd 、 λ、控制器由比例系数微分阶次 kp 、积分系数构成，其传递函数为: ， ( + kd sμ; = kp + 控制器的系统模型如图 μ ki / sλ) λ ＞ 0 所示，其中: ) 为控制器输出， G1 μ ＞ 0 ( r ( 1 ( 7 ) ) 为系统 t ) 为被控 s FOPID 积分阶次 ) ( s Gc FOPID 输入， ( e 对象， ( y t t ) 为控制器输入， u ) 为系统输出 ( t 。图 1 FOPID 控制系统模型 Fig． 1 FOPID control system model 2 标准 PSO 算法及改进 2． 1 算法原理粒子群优化算法［觅食行为演变而来的一种基于群体协作化搜索算法。PSO 索空间中总共有粒次迭代时的位置表示为 D n { 15 ］，是模拟自然界鸟群或鱼群等生物的信息共享的随机优、维( 维度代表优化参数的个数) 搜算法在个微粒构成随机搜索种群，搜索种群中微 } ，其中 xk xk i = ，次迭代时的速度为微粒第 i D。次迭代及其之前的最优个微粒在， } ，也称为 pbestk 次迭代时群体中所有微粒所到达的最佳位 } 表示，也简称为次迭代时粒子的速度，， … 2 } ，第， gbestk ， pbestk ， … ， … pbestk ， xk ， xk i = i { k k id id i2 i1 i2 i1 2 d 截止到第 pbest。置用 gbestk = 标准和位置 PSO xk +1 gbest。 vk +1 i i gbestk ， gbestk k { ， … 算法迭代过程中第按照式( ) 1 ( 、 8 vk +1 id = w·vk id + c1 ·r1 · d － xk ) id ( gbestk id + vk +1 id xk +1 = xk k + 1 ) 进行迭代更新。 pbestk id － xk id ) 9 ( + c2 ·r2 · ) ) 为粒子的学习因 ( ( 8 9 id w 和在 c1 = c2 = 为粒子运动的惯性权重系数; 其中: 子( 或加速度系数，或学习能力系数) ，经典取值为 ; ) 的随机取值是在( 和 c2 c1 ， 1 0 2 r1 。 xk i 、 r2 PSO 迭代的位置位置粒子个体的最优位置有关，还与粒子的惯性权重系数有关算法迭代过程中，粒子的搜索速度不仅和上一次粒子种群的最优和为防止粒子的迭代速度过快，算法早熟收敛， c2 、r1 。越过全局最优位置，对粒子的速度加以约束，粒子速度约束条件为式( ) ，设置粒子速度的上下限，将粒子的范围限定在［， vmax 学习因子 gbest 和 pbest、 10 ］ w、 vmin 。 c1 r2 { vmin vk +1 id ，，， vk +1 id = id vk +1 ＜ vmin vmin ≤ vk +1 vk +1 max id ≤ vmax ＞ v 2． 2 惯性权重系数的改进 vmax id ( ) 10 13 1 分数阶的定义［定义和］有，而分数阶中积分阶次和微定义、定对任。分数阶定义 Grunwald-Letnikov Caputo ，Ｒiemann-Liouville 定义是最常用的分数阶定义 i 第， 2 { vk k ， … ， vk ，， i = 1 n d = 1 ， vk … i = 位置表示为 pbestk ， vk id i1 i2 整数阶微积分的阶次均为分阶次为任意正实数。定义、Ｒiemann-Liouville m － 1 ＜ α ＜ m ) Cauchy 义，其中意实数中积分表达式为式( Ｒiemann-Liouville ， m ∈ N 微分表达式为式( 、 ( ) ∫ 1 n － β 1． 2 Oustaloup 近似方法 ) α －1 f t － τ ［ ) dn ∫ dtn τ t － τ a Dα a Dβ τ ( t f t f 1 ( Γ Γ = = 1 a ( ) ( ) ( ) ( ( t t f a a t t ) 2 。 dτ ］ ) ) β －m dτ ( ( ) ) 1 2 9 8 10 PSO PSO 等［］对。 ( FOPID 控制器文献［高嵩等［腾志军等［ LQＲ淘汰部分个体的改进］使用线性二次型调节器 ( ) 优化， Linear Quadratic Ｒegulator ］提出一种按适应度大小 ) 优化 Partiele Swarm Optimization 算法中的学习因子引入动态加 FOPID。速因子，提高算法全局搜索能力，使得算法能以更快的速度搜］采用自适应惯性权值调节的方索到全局最优解式对粒子群优化算法进行改进，并应用在磁悬浮系统中的模糊控制系统的量化因子的参数优化上，最终获得较好的控制］针对永磁同步电机的关键参数估计问题，提效果出一种带学习策略的动态粒子群算法，同时设计一种具有可变探测矢量的运动修正方程，有效地更新粒子，使群体能够以较大的概率覆盖大范围的搜索空间，从而提高了全局搜索能力。Liu 等［。 11 12 。 FOPID 为应对参数整定的复杂性和不确定性，本文提出 FOPID 参数的方法，对粒子群算法的惯性改进的粒子群优化权重系数和学习因子进行改进，分别设置惯性权重系数的最大值和最小值的范围，并且惯性权重系数的最大值和最小值的范围随算法迭代次数以伽玛函数方式非线性下降，同时每个粒子的惯性权重系数和学习因子依据该粒子的适应度值进行动态调整，以此实现提高算法的收敛速度和收敛精度的目的 1 分数阶控制系统数学基础 1． 1 分数阶微积分定义。由分数阶微积分的定义可以精确计算给定输入的微积分，但不便于在实际应用中实现，需对其近似化处理分数阶微积分项可以用有限维的整数阶来近似处理，其中较为常用的是。设需要近似处理的传递函数］，且 ) ］后 ) γ，设定微积分近似拟合频段为［ ) 1 /2 ，， ωh 近似方法［近似方法 Oustaloup ，采用 s / ωu ωb 。 G = ( ( ( 14 s 0 ＜ γ ＜ 1 Oustaloup ωu = ωb·ωh 的传递函数为: ( ) s N = K∏ k = －N G 其中: s + ωz s + ωp k k ( K = ωb / ωh ( ωz k = ωb ωh / ωb ( ωp k = ωb ωh / ωb 1． 3 FOPID 控制器 k k = N ωp ) －γ /2 ∏ ωz ( ) k +N +0． 5 k = －N k 1 －λ 2N +1 ( 2N +1 ) k +N +0． 5 1 +λ ( ) 3 ( ( ( ) ) ) 4 5 6 ) ) FOPID 控制器相对于整数阶而言引入两个新的系 PID 算法迭代中惯性权重系数是最重要的参数，影响 w PSO

897 计算机应用第 39 卷 w 标准 16 ］ w 。可以改变惯性权重系数算法的收敛速度和收敛精度，因而惯性权重系数的取值至关使得微粒迭代过程中保持运动的重要［惯性，通过调整惯性权重系数算法的空间搜全局搜索能力提高，有效越大，索能力惯性权重系数 w 避免陷入局部最优; 当较小时，全局收敛速度下降，但可以 w 提高是标准的收敛精度 w 按迭代次数的增加依次线性减小，其变化过程按式( ) 进行: 算法中惯性权重系数 PSO PSO PSO PSO 。。 11 w ( ) k wmin － wmax 为算法的当前迭代次数; ( ) k = wmax + w 其中: 次迭代时的惯性权重; k 为惯性权重系数重系数 w 的最小值，通常为 kmax 的最大值，通常为 · ( k w 0． 4。为算法最大的迭代次数; ( ) 11 k / kmax ( ) ) 是种群中所有粒子在第迭代迭代为惯性权 wmax ; 0． 9 wmin PSO 但是。算法中惯性权重的取值在一定程度上满足算法迭代要求: 在迭代的开始阶段为保证种群搜索空间的拓展能力，需要粒子保持较高的运动惯性，随迭代次数增加粒子运动惯性下降，相应地提高算法的收敛精度算法在实际的迭代过程中其收敛稳定时的迭代次数要远小于预先设置的最大迭代次数，即算法优化目标( 适应度值) 趋于稳定的速度要远大于惯性权重系数下降的速度，在算法迭代的后期惯性权重系数的变化对算法收敛的快速性和精确性没有实质性的同时，在迭代过程中对所有的粒子使用相同的惯性权重影响。系数不利于提高算法的收敛速度和收敛精度，对于不同适应度大小的粒子，其运动惯性应有所区别 PSO 。 w w w ) : PSO1 针对惯性权重系数进行以下两点改进( 简称改进随迭代次数线性下降和同一次迭代相同的不足，本文提出对惯时对不同的粒子惯性权重系数 ) 对惯性权重系数性权重系数的最大值和最小值分别设置上下限范围，并且随 ) 在迭代过程中，对不迭代次数按伽玛函数［在其范围内按粒子适应度同适应度的粒子其惯性权重系数具体如下: 第大小进行动态调整次迭代时惯性权重系数。最大值为，［ max 、wk wmaxup wmaxdown 限范围内随迭代次数按伽玛函数逐渐减小，如式( ，最小值为］，［ wk max ∈ 在其上下 ) ，上下限范围分别是］非线性降低; ， wminup ］， wk wmindown min ∈ wk wk wk w max w min min 1 2 k ) 17 wk max = wmaxdown + wk min = wmindown + ( ( ) 式( 12 ］， wk ( 、 13 max 、wk min ) 中 γ 为第 k ( 、 ) ( ) 13 12 1 － / kmax k － 1 ( · wmaxup － wmaxdown 。 ) γ ) 12 ) γ ) 的经典取值范围为次迭代时惯性权重系数的最大值和为伽玛变换系数， γ wminup － wmindown ( · k － 1 / kmax 1 － 13 ( ) ( ) ( ［， 2 10 最小值设取值为所示。 wk max ∈ ［ 0． 7 ， 1． 2 ］时对应的［、wk 0． 3 min ∈ wk max 、wk 越大， wk γ 的下降速度越快 max 、wk min min 2、3、4、5、6 由图 2 2 。数就越少，即中可知。］， 0． 6 则、kmax = 50、 γ 和迭代次数的关系如图靠近其下限的迭代次惯性权重系数的上下限按伽玛函数逐渐减小而对于。单个粒子的惯性权重系数按粒子的适应度大小进行动态调整，粒子的适应度越大，表明粒子处于较优的位置，应降低，保证粒子的收敛精度; 而粒子的适应度越惯性权重系数 wi w wk max 、wk w max 小，表明粒子远离较优位置，为提高粒子的收敛速度，此时应将所有粒子按其适应度值从小增大粒子的惯性权重系数，到大的顺序排列，粒子，， 2 … ，排由式 n 对应的惯性权重系数的适应度排列序号为 i = 1 w。 ti ( i i wi 为种群规模) ，则粒子 ) 计算得到 n ( 14 ( ) wi = wmax + 从式( 越小; 粒子的适应度越低，其惯性权重系数 ) ) 可知粒子的适应度越高，其相应的惯性权重系越大，惯性 wmin － wmax 1 － ti / n 数系数的动态取值使粒子具有合适的运动惯性 · 14 14 w w ) ( 。 ( 。图 2 wmax 和 wmin 的下降趋势 Fig． 2 Downward trend maps of wmax and wmin 1 。。。2 PSO 惯性系数权重改进后具有如下优势: ) 采用伽玛函数使惯性权重系数的最大值和最小值按迭代次数非线性降低，在迭代次数较低时具有较快的下降速度，随迭代次数的增加其使得算法前期需要保持较大的运动惯下降速度逐渐降低性，提高整个种群的空间拓展能力，算法后期降低粒子的运动惯性，提高算法的收敛精度算法适应度值得变化趋势大致相同，使得算法可以在最短的时间内收敛 ) 单个粒子的惯性权重系数按其适应度的大小趋于稳定动态取值，粒子的适应度越高，惯性权重系数越小; 粒子的适应度越低，惯性权重系数使得粒子保持较为合理的运动惯性，提高种群的进化速度和进化精度 2． 3 学习因子的改进该变化趋势与越大 pbesti 越大，粒子学习因子靠近其个体最优位置的能力加强，即粒子加强对本身的思考，自身认知能力提高，粒子的迭代行为表现得越发独立，在搜索空间上分散现象就越明算法迭代进化过程变得越慢，迭代次数增加，容显，同时易陷入局部最优靠近种群最优位置的能力加强，社会意识能力加强，种群中粒子之间信息 gbest 共享的力度加强，迭代中粒子间的差异就越小，在搜索空间上聚集现象越明显，算法进化速度越快，迭代次数减小，容 PSO 易越过全局最优位置［］学习因子。越大，粒子 PSO 。。 c2 c1 w w 18 i i 。

第 3 期金滔等: 改进的粒子群优化算法优化分数阶 PID 控制器参数 997 16 PSO c1 、c2 c1 、c2 学习因子 ) : 在改进 c1 、c2 的合理取值对标准。影响着粒子对自身的认知能力和社会的认知能力，算法进化速度和收敛精度中学习因子的取值为的提高具有重要的作用 PSO 固定值，不具有自适应调整的能力本文对学习因子进行如下。方法的基础之上，对学习改进( 简称改进因子粒子的适应。度越大，说明粒子本身为处于较优的位置，此时粒子应该加强对自身的认知能力，即增大学习因子 ; 而粒子的适应度越小，表明粒子处于较劣的位置，此时粒子应加强对社会的认知能力，即增大学习因子 ( 按照粒子的适应度大小进行动态调整的值由式( 学习因子 ) 确定: c1 、c2 PSO2 PSO1 c2 。和 15 c1 c1 c2 ) 、 ) ) c1max － c1min · ( ( · 的学习因子; c2max － c2min ( ( 为粒子 ci 1 = c1min + ci 2 = c2min + 其中: ci 1 、ci 的最小值，本文取值均为最大值，本文取值均为 2． 5 为种群规模( 粒子的总数) i 2 0． 5 ; ti 。 ) ( ( ) ) 15 16 为学习因子 1 － ti / n ) ti / n c1min 、c2min 为学习因子的适应度的排列序号; c1 、c2 的 c1 、c2 n ; c1max 、c2max 为粒子 i 。对学习因子改进后具有如下两方面的优势: 一方面有利于粒子根据自身的适应度增加或降低粒子向社会和自身的学习能力，提高粒子本身在整个群体中的适应能力; 另一方面学习因子的动态调整可以有效地避免种群陷入局部最优或克服算法早熟收敛等缺点，使得整个种群向更优的方向进化，便于得到更优的解 3 改进的 PSO 优化 FOPID 控制器参数 3． 1 优化参数及优化目标算法优化分数阶微分系数将 μ。 ki 、作为粒子的输入，即粒子参数空间的维度为 kp 、 5。算法的参数优化是给定优化目标函数并在目标空间中搜 kp 、 ki 、kd 、λ、μ、 PSO 索出满足最优目标参数的过程控制器的参数包含比例系数积分阶次微分阶次积分系数 kd 、 PSO λ、 PID 。控制器的性能指标包含调节时间稳态误 FOPID 、以时间和误差绝对值的积分作为优化目标，可使得控制差等。以系统输出的最大值作为优化目标器具有较好的动态性能。可以有效防止系统的超调因而所得的优化目标为式( 。超调量、 ) : 改进 PSO ) 后优化算法中惯性权重系数和学习因子 ( 即改进的算法的流程如图所示改进 3 。 PSO1 PSO2 在改进 FOPID 步骤中省略第 ) 初始化粒子群参数 PSO2 1 最大值值值的范围［ c2min 、和最小值 c1max c2 惯性权重系数最大值的范围［ c1min 、 ) 步，改进 7 最大迭代次数。学习因子具体步骤如下 PSO2 学习因子 kmax 、的最大值， wmaxup c2max wmaxdown 粒子速度的范围［ c1 。的和最小］和最小，， wminup ］种群规模、］ vmax wmindown n、粒子的随机初始速度和初始位置、 ) 计算粒子适应度值: 利用粒子的位置( 优化参数) 对 ) ) 计算每个粒控制系统进行阶跃响应，根据优化目标( 式( vmin 。 2 17 ( ) J = α1 ·∫ e ( e t ) 为控制器为权重系数，本文中其中: 出， 3． 2 改进 PSO 算法的优化步骤 α1 、α2 t t ( ( ) ) t dt + α2 ·max 时刻的输入偏差值， ( y y t α1 = 0． 4、α2 = 0． 8。 17 ( ) 17 ) 为系统的输 t 子的适应度值 Ji 。 3 ) 更新个体最优位置: 粒子当前的适应度值与其个体比较，如果较好，则将当前适应度值作为 i 最优适应度值个体最优值，并保存该位置 pbesti 。 4 ) 更新种群最优位置: 粒子当前的适应度值与种群最比较，如果较优，则将当前适应度值作为种 i 优适应度值群最优值，并保存该位置 gbest 。式( 5 12 6 ( 、 ) 计算 ) 计算惯性权重系数的最大值和最小值: ) ) 计算粒子惯性权重系数: 对种群中所有粒子的适应度的惯性 ) 计算出粒子 max 、wk 根据 wk 。 13 min 值从小到大进行排序，然后根据式( 权重系数 14 i wi 。 7 ) 计算粒子学习因子: 粒子 ( 、 ) 更新粒子速度和位置: ) 计算。 16 的学习因子 i ci 1 、ci 2 根据式 vk +1 id 、xk +1 id 根据迭代式( ) 和( 8 ) 9 ( ) 15 8 计算。 ) 粒子速度约束: 由式( ) 迭代是否结束: 如果到达最大迭代次数 ) 确定。 10 9 10 则退出; kmax 否则返回第 ) 步继续迭代 2 。图 3 参数优化步骤 Fig． 3 Steps of optimizing parameters 4 仿真结果与分析为验证改进的算法的对 PSO FOPID 控制器的控制效果，选取典型的二阶系统作为被控对象，其传递函数为: ( ) 18 ( ) 1． 6 s = G1 仿真实验中，算法最大迭代次数 s2 + 2． 584s + 1． 6 ，种群的规模 kmax = 50 ，粒子速度最小值，学习因子 vmin = 最小值 c1 最小值下限 n = 20 ，粒子更新速度最大值最大值，粒子学习因子－ 4 c1 ，学习因子 vmax = 4 c1max = 2． 5 c2min = c2max = 2． 5、 c1min = 0． 5 的最大值，惯性权重系数最大值的上限和最小值的上限 c2 ［［［ 0． 1 0． 1 0． 5 ， 5 λ ∈ ］， kd ∈ ， 2． 0 0． 5 ［ wminup = 0． 6、 γ = 6。］， wmindown = 0． 3 ， 10 wmaxup = 1． 2、下限目标优化参数的取值范围， 2． 0 wmaxdown = ，伽玛系 0． 7 ］，数 kp ∈ ki ∈ ］，［］，， 0． 5 2． 0 0． 1 控制系统输入信号为阶跃响应，分别用标准改进算法、惯性权重系数的改进惯性权重系数、 ) 对控制系统进行迭代优及学习因子的化每种算法的优化参数对控制系统的单位阶跃响应从平均超调量平均稳态误差和平均迭代次数这四项性能、次，三种算法总共运行平均调节时间、对每一种算法运行算法( 改进算法( 改进 PSO2 PSO1 μ ∈ PSO PSO PSO 次。。 10 30 )

008 计算机应用第 39 卷 1 11 所示指标进行对比，结果如表 1 中可知: 改进从表 PSO2 次，相比于其他两种算法具有较快的收敛速度。算法平均收敛的迭代次数为改进算法优化分数阶控制器参数后，其平均超调量为，平均稳态误差为的综合性能最 0． 789 9 s 对比其他两种算法，改进，平均调节时间为 0． 048 7 PSO2 。 PSO2 － 0． 000 65。优。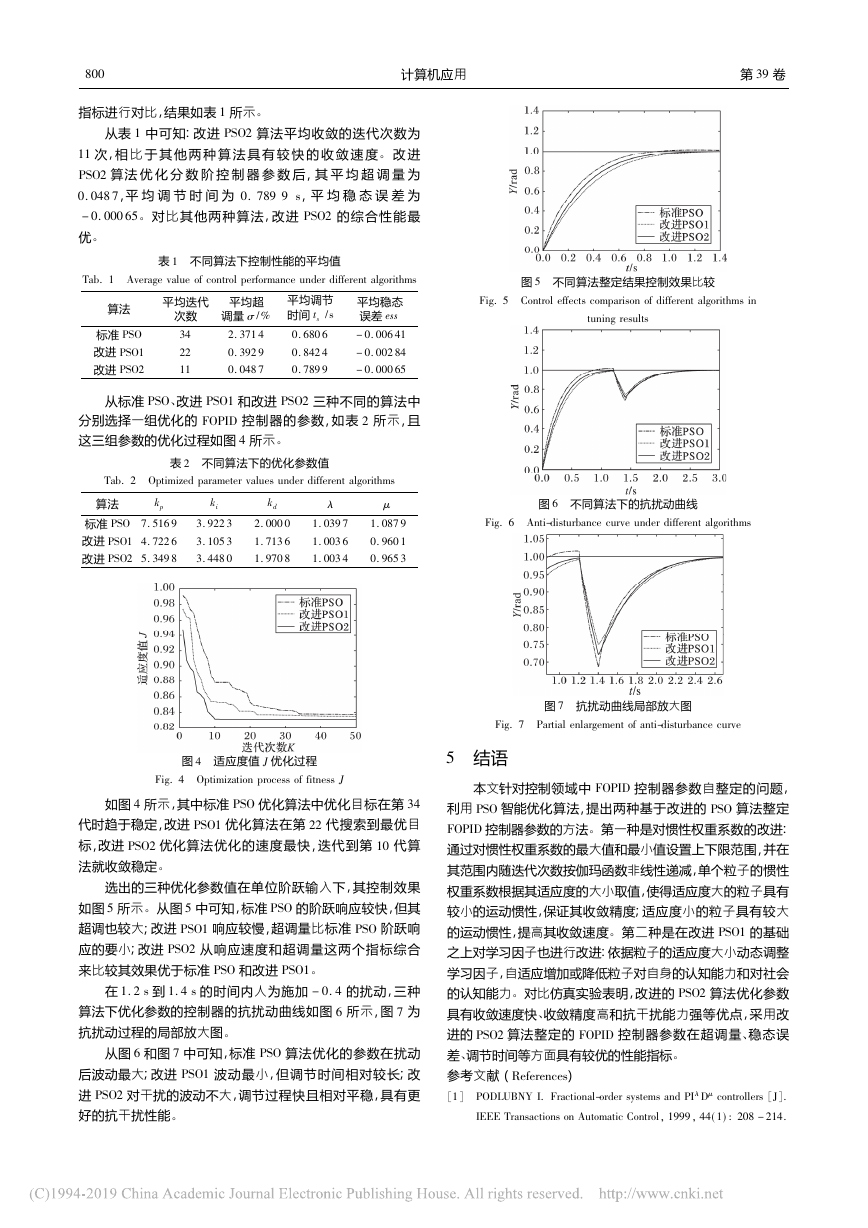表 1 不同算法下控制性能的平均值 Tab． 1 Average value of control performance under different algorithms 算法标准改进改进 PSO PSO1 PSO2 平均迭代平均超次数调量 σ / % 平均调节时间 ts / s 34 22 11 2． 371 4 0． 392 9 0． 048 7 0． 680 6 0． 842 4 0． 789 9 平均稳态误差 ess － 0． 006 41 － 0． 002 84 － 0． 000 65 图 5 不同算法整定结果控制效果比较 Fig． 5 Control effects comparison of different algorithms in tuning results PSO、从标准改进分别选择一组优化的 FOPID 这三组参数的优化过程如图 PSO1 PSO2 和改进控制器的参数，如表所示三种不同的算法中所示，且 2 4 。表 2 不同算法下的优化参数值 Tab． 2 Optimized parameter values under different algorithms 算法 kp ki kd λ μ 图 6 不同算法下的抗扰动曲线标准改进改进 PSO 7． 516 9 3． 922 3 2． 000 0 1． 039 7 1． 087 9 Fig． 6 Anti-disturbance curve under different algorithms PSO1 4． 722 6 3． 105 3 1． 713 6 1． 003 6 0． 960 1 PSO2 5． 349 8 3． 448 0 1． 970 8 1． 003 4 0． 965 3 图 4 适应度值优化过程 J Fig． 4 Optimization process of fitness J 如图所示，其中标准优化算法中优化目标在第 PSO 优化算法在第 PSO1 22 34 代搜索到最优目代算 10 优化算法优化的速度最快，迭代到第 4 代时趋于稳定，改进标，改进 PSO2 法就收敛稳定。 5 。所示选出的三种优化参数值在单位阶跃输入下，其控制效果的阶跃响应较快，但其阶跃响从响应速度和超调量这两个指标综合响应较慢，超调量比标准中可知，标准如图从图超调也较大; 改进应的要小; 改进来比较其效果优于标准和改进 PSO2 PSO1 PSO PSO 5 PSO PSO1。在到 1． 2 s 1． 4 s 的时间内人为施加－ 0． 4 算法下优化参数的控制器的抗扰动曲线如图抗扰动过程的局部放大图 6 。的扰动，三种所示，图为 7 中可知，标准算法优化的参数在扰动波动最小，但调节时间相对较长; 改对干扰的波动不大，调节过程快且相对平稳，具有更 PSO1 PSO 6 从图和图 7 后波动最大; 改进进好的抗干扰性能 PSO2 。图 7 抗扰动曲线局部放大图 Fig． 7 Partial enlargement of anti-disturbance curve 5 结语。 PSO PSO 利用 FOPID 控制器参数的方法本文针对控制领域中智能优化算法，提出两种基于改进的控制器参数自整定的问题，算法整定第一种是对惯性权重系数的改进: FOPID 通过对惯性权重系数的最大值和最小值设置上下限范围，并在其范围内随迭代次数按伽玛函数非线性递减，单个粒子的惯性权重系数根据其适应度的大小取值，使得适应度大的粒子具有较小的运动惯性，保证其收敛精度; 适应度小的粒子具有较大的运动惯性，提高其收敛速度的基础之上对学习因子也进行改进: 依据粒子的适应度大小动态调整学习因子，自适应增加或降低粒子对自身的认知能力和对社会的认知能力算法优化参数收敛精度高和抗干扰能力强等优点，采用改具有收敛速度快、稳态误进的、差参考文献 ( 调节时间等方面具有较优的性能指标、对比仿真实验表明，改进的控制器参数在超调量第二种是在改进算法整定的 FOPID PSO1 PSO2 PSO2 。。。 ) Ｒeferences ［1］ PODLUBNY I． Fractional-order systems and PIλ Dμ controllers ［J］． IEEE Transactions on Automatic Control， 1999， 44( 1) : 208 － 214．

第 3 期金滔等: 改进的粒子群优化算法优化分数阶 PID 控制器参数 108 ［2］ PETＲAS I． The fractional-order controllers: methods for their syn- ［13］ KHIABANI A G， BABAZADEH Ｒ． Design of robust fractional-or- thesis and application ［EB / OL］．［2018-07-03 ］． https: / / arxiv． der lead-lag controller for uncertain systems ［J］． IET Control Theo- org / pdf / math /0004064v1． pdf． ry and Applications， 2016， 10( 18) : 2447 － 2455．［3］ MONJE C A， CALDEＲON A J， VINAGＲE B M， et al． On frac- ［14］ OUSTALOUP A， LEVＲON F， MATHIEU B， et al． Frequency- tional PIλ controllers: some tuning rules for robustness to plant un- band complex noninteger differentiator: characterization and syn- certainties ［J］． Nonlilnear Dynamics， 2004， 38( 1 /2 /3 /4) : 369 － thesis ［J］． IEEE Transactions on Circuit and Systems—I: Funda- ［4］ 381．李新波付云博，堆控制中的应用，姜良旭等．，光学精密工程［J］．神经网络分数阶 PIμ Dλ 在压电叠，2015，23( 12) : 3439 － 3445．［15］ mental Theory and Applications， 2000， 47( 1) : 25 － 39．麻荣永法张智超．参数特性分析数学计算基于粒子迭代位移和轨迹的粒子群算杨磊磊，，，2013，2 ( 4) : 109 － 115． C1、C2 ［J］． ( LI X B， FU Y B， JIANG L X， et al． Application of neural network ( MA Ｒ Y， YANG L L， ZHANG Z C． Analysis the characteristic of fractional order PIμ Dλ to piezoelectric stack control ［J］． Optics and C1， C2 based on the PSO of iterative shift and trajectory of particle Precision Engineering， 2015， 23( 12) : 3439 － 3445． ) ［5］ ZHANG F， YANG C， ZHOU X， et al． Fractional-order PID con- ［16］ troller tuning using continuous state transition algorithm［J］． Neural ［J］． Mathematical Computation， 2013， 2( 4) : 109 － 115． ) 赵延龙基于二次搜索的改进粒子群算法，算机应用于振华滑楠，．，2017，37( 9) : 2541 － 2546． ( ZHAO Y L， HUA N， YU 计［J］．［6］ Computing and Applications， 2018， 29( 10) : 795 － 804．张欣基于量子粒子群优化设计的分数阶 PIλ Dμ 控制器，2018，25 ( 3 ) : 493 － 498． ( ZHANG X， ZHONG C 仲崇权，．控制工程［J］． Z H． Improved particle swarm optimization algorithm based on twice search ［ J ］． Journal of Computer Applications， 2017， 37 ( 9) : 2541 － 2546． ) Q． Fractional order PIλ Dμ controller design based on quantum parti- ［17］ SHAO Z， KLAVZAＲ S， LI Z， et al． On the signed Ｒoman k-dom- cle swarm optimization ［J］． Control Engineering of China， 2018， 25 ination: complexity and thin torus graphs ［ J ］． Discrete Applied ( 3) : 493 － 498． ) ［7］ AGHABABA M P． Optimal design of fractional-order PID controller ［18］ for five bar linkage robot using a new particle swarm optimization al- Mathematics， 2017， 233: 175 － 186．赵远东，算机应用方正华．带有权重函数学习因子的粒子群算法计［J］．，2013，33( 8) : 2265 － 2268． ( ZHAO Y D， FANG Z H． gorithm ［J］． Soft Computing， 2016， 20( 10) : 4055 － 4067． Particle swarm optimization algorithm with weight function＇s learning ［8］ DAS S， PAN I， DAS S． Multi-objective LQＲ with optimum weight factor ［J］． Journal of Computer Applications， 2013， 33( 8) : 2265 selection to design FOPID controllers for delayed fractional order － 2268． ) ［9］［10］ processes ［J］． ISA Transactions， 2015， 58: 35 － 49．高嵩整定陈超波控制工程一种改进粒子群优化的分数阶王磊等，，，．［J］．，2017，24( 10) : 2010 － 2015． ( GAO S， WANG 参数 PID This work is partially supported by the Key Project of Sichuan Science and Technology Department ( 2018JY0463) ， the Scientific Ｒesearch Inno- L， CHEN C B， et al． An improved particle swarm optimization algo- vation Team Project of Sichuan Colleges and Universities ( 18TD0024) ， the rithm for fractional order PID parameter tuning ［J］． Control Engi- Industrial， Academic and Ｒesearch joint Laboratory of Chengdu SIWI neering of China， 2017， 24( 10) : 2010 － 2015． ) 滕志军，算法研究，微电子学与计算机郭力文吕金玲等，．［J］．基于动态加速因子的粒子群优化，2017，34 ( 12 ) : 125 － 129． High-Tech Industry Company Limited and Xihua University ( 2016-YF04- 00044-JH) ， the Innovation Fund for Postgraduates in Xihua University ( ycjj2018073) ． ( TENG Z J， LYU J L， GUO L W， et al．Ｒesearch on particle swarm optimization based on dynamic acceleration coefficients ［J］． JIN Tao， born in 1992， M． S． candidate． His research interests in- Microelectronics and Computer， 2017， 34( 12) : 125 － 129． ) clude intelligent algorithm， intelligent control．［11］ ZHANG S， MA S， SONG N， et al． Fuzzy sliding mode control DONG Xiucheng， born in 1963， M． S．， professor． His research in- based on PSO for magnetic levitation positioning stage ［J］． IEEE terests include intelligent control， robot control． Transactions on Electrical and Electronic Engineering， 2018， 13 LI Yining， born in 1995， M． S． candidate． His research interests ( 10) : 1492 － 1500． include robot control．［12］ LIU Z-H， WEI H-L， ZHONG Q-C， et al． Parameter estimation for ＲEN Lei， born in 1995， M． S． candidate． His research interests in- VSI-fed PMSM based on a dynamic PSO with learning strategies clude digital image processing．［J ］． IEEE Transactions on Power Electronics， 2017， 32 ( 4 ) : FAN Peipei， born in 1994， M． S． candidate． Her research interests 3154 － 3165． include machine vision．

分享到：

赞收藏

资料库

PSO算法PID整定.pdf

相关推荐

课程资源

热门标签

最新资料