基于MATLAB切比雪夫I型滤波器设计.doc-资料库

cskaiven-928019-16359647636592877846.doc.pdf-第1页.png

第1页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第2页.png

第2页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第3页.png

第3页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第4页.png

第4页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第5页.png

第5页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第6页.png

第6页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第7页.png

第7页 / 共13页

cskaiven-928019-16359647636592877846.doc.pdf-第8页.png

第8页 / 共13页

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页基于 MATLAB 切比雪夫 I 型滤波器设计学生姓名：指导老师：摘要在现代通信系统中，由于信号中经常混有各种复杂成分，所以很多信号的处理和分析都是基于滤波器而进行的。而滤波器的种类很多，从功能上可将滤波器分为低、带、高、带阻类型。从实现方法上可分为 FIR、IIR 类型。从设计方法上可分为 Chebyshev(切比雪夫）,Butterworth（巴特沃兹）。而本次课程设计上要用到的切比雪夫滤波器是在通带或阻带上频率响应幅度等波纹波动的滤波器。在通带波动的为“I 型切比雪夫滤波器”，在阻带波动的为“II 型切比雪夫滤波器”。关键词模拟；低通滤波器；IIR； 1 引言 IIR 滤波器设计技术依靠现有的模拟滤波器得到数字滤波器，工程实际当中把这些模拟滤波器叫做滤波器原型。在工程实际中应用最广泛的有两种模拟滤波器，即巴特沃斯滤波器和切比雪夫滤波器。本次课程设计就讨论切比雪夫滤波器的特性以及用 MATLAB 实现的方法。 1. 1 课程设计目的本课程设计主要是使学生增进对 MATLAB 的认识，加深对数字信号处理理论方面的理解，使学生了解数字信号处理 IIR 滤波器的设计和掌握用 MATLAB 实现 IIR 滤波器的设计方法、过程，为以后的工程设计打下良好基础。 1.2 课程设计要求设计程序时，应以理论作为指导，构思设计方案；设计完成后应进行调试，仿真和分析；处理结果和分析结论应该一致，而且应符合理论；独立完成课程设

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页计并按要求编写课程设计报告书。 1.3 课程设计内容进一步学习低通滤波器的原理，在通信系统仿真软件 MATLAB 平台上，设计出 IIR 模拟低通滤波器，对设计项目进行调试，对程序进行仿真，对结果结合理论进行分析。 2.1 滤波器介绍 2 IIR 滤波器预备知识 IIR 滤波器具有无限长脉冲响应，因此能够与模拟滤波器相匹敌；一般来说，所有的模拟滤波器都有无限长脉冲响应。因此，IIR 滤波器设计的基本方法是利用复值映射将大家熟知的模拟滤波器变换为数字滤波器。这一方法的优势在于各种模拟滤波器设计（AFD）表格和映射在文献中普遍能够获得。这个基本方法也称为 A/D（模拟-数字）滤波器变换。然而，AFD 表格仅对低通滤波器适用，而同时也想要设计其他频率选择滤性波器。为此，需要对低通滤波器实行频带变换，这些变换也是复值映射，在各种文献中也能得到。这种 IIR 滤波器设计的基本方法存在两种主要途径。途径一：1.设计模拟低通滤波器，2.实行频带变换，3.实行滤波器变换。途径二：1.设计模拟低通滤波器，2.实行滤波器变换，3.实行频带变换。模拟滤波器的设计指标以及在模拟滤波器的技术要求中所用到的幅度平方响应，这将导致三种广泛采用的模拟滤波器特性，即巴特沃兹（Butterworth），切比雪夫（Chebyshev）和椭圆（Elliptic）滤波器。然后再将这些原型模拟滤波器转换到不同的频率选择性数字滤波器。 2.2 相对线性标尺设 aH ( j 是某个模拟滤波器的频率响应，那么低通滤波器在幅度平方响应 ) 上的技术指标给出为：

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页 1 2 1   0 | H (  a | H (  a j   j 2   ) | 1 ，|  |  p ， s   | | 2 ) | 1 2 A 式中是通带波纹参数， p 是通带截止频率一 rad/s（弧度/秒）计，A 是阻带衰减参数，以及 s 是阻带截止频率以 rad/s 计。这些参数如图 2.1 所示。图 2.1 模拟低通滤波器技术指标要求 2 由图可见， | H ( a 2  ) |  ) | j 必须满足 1 2 1   1 2 A ) |   j j p p 2 | H ( a | H ( a ，    p ，    s 参数和 A 是分别与以 dB 计的参数 pR 和 sA 有关的，这些关系是 pR   10log 10 sA   10log 10 1 2 1   1 2 A    pR 10 10  1 （2-1）   A 10 sA 20 （2-2）波纹 1 和 2 的绝对标尺是通过下式与和 A 有关的： 1 1    1  2  1 2   1    2 1   1  1

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页  2   1 1    A 1 A 1  1   2 3 切比雪夫 I 型滤波器 3.1 切比雪夫滤波器参数切比雪夫 I 型滤波器的振幅平方函数为： A(  2 )= H ( a j 2   ) 1 1  2 2 v N      C 式中 C 为有效带通截止频率，是与带通波纹有关的参量，大，波纹大，0<<1; )  为 N 阶切比雪夫多项式。 N ( 有关参数的确定：（1）预先给定带通截止频率 C ；（2）确定。通带波纹表示成： ) ( H j  ) ( H j  10lg 20lg max 2    2 a a min a ( H j ( H j )  )  a 所以   10lg(1  2 2   ),  10 0.1 1  2 max 2 min  20lg 1 1 1  2  )dB 分贝数后，可求得 2 。给定通带波纹值 ( （3）由阻带的边界条件确定阶数 N. 设 s ， 2A 为事先给定的边界条件，即在阻带中的频率点 s 处，要求滤波器频响衰减达到 21 A 以上。    ， s aH j  ( ) 2 21 A 即由此得 1 1  2 2 v N      C  21 A

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页因此， v N      C  2 1 A   X  , 1    =cosh( N ( 1 ) N arccos hx ) N  arccos ( 2 1 Ah   arccos ( h s  c )  ) 因此，要求阻带边界频率出衰减越大， N 也越大。参数 N ， c ，给定后，查阅有关模拟滤波器手册，就可以求得系统函数 ( ) aH s 。 MATLAB 提供了[Z，P，K]=cheblap（N，Rp）函数来设计 N 阶通带波纹为 Rp 的归一化切比雪夫 I 型模拟原型滤波器，并得到数组 Z 和 P（即零点和极点）以及增益值 K。我们需要一个具有任意 c 的非归一化的切比雪夫 I 型滤波器。这可以通过将这个归一化滤波器的数组 P 倍乘以 c 来完成。和巴特沃兹原型滤波器相类似，这个滤波器没有零点。新的增益 K 利用式子： ( 0) aH j =1，N 为奇数或 aH j ( 0)  1  1 2  ，N 为偶数确定这可通过将原来的 K 倍乘以非归一化分母多项式对归一化分母多项式的比在 s=0 的求值来完成。下面的函数称为 U-chblap（N，Rp，Omegac），用于设计一个非归一化的切比雪夫 I 模拟原型滤波器，得到直接的 ( ) aH s 。 function[b，a] = u chblap(N，Rp，Omegac); %[b，a] = u chblap(N，Rp，Omegac) b = numerator polynomial coefficients a = denominator polynomial coefficients N = order of the elliptic filter % % % % Rp = passband ropple in dB; Rp > 0 % Omegac = cutoff frequency in radians/sec % [z，p，k] = cheblap（N，Rp）； % % % % p = p*Omegac; aNu = a(N+1); a = real(poly(p)); aNn = a(N+1);

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页 % % % % k = k*aNu/aNn; b0 = k; B = real(poly(z)); b = k*B； 3.2 滤波器设计方程已知 p ， s ， pR 和 sA ，有三个参数就可以确定一个切比雪夫 I 型滤波器，根据相对线性标尺中的 2-1 与 2-2 式我们可得到： 10 sA  根据上面以前讨论的性质有： 1  和 A  10 pR 10 20 阶 N 给出为 c = p 和   r   s p g  2 A  21  N       log log 10 10   2 g g   1       r 2 r   1        4 滤波器设计实现 4.1 滤波器设计过程设计一个低通的切比雪夫 I 型低通滤波器满足：通带截止频率： p =0.2π；通带波纹： pR =1dB 阻带截止频率：  0.1*1 10  =0.3π；阻带波纹： sA =16dB 1 我们首先计算必要的参数：  0.1*1 10  =0.5088，A= 1 16 10 =6.3096 20 c = p =0.2π, r = 0.3  0.2  =1.5 g  2 A  21  =12.2429,N=4 现在能确定 ( ) aH s ，

孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页  = 1  + 1  1 2  = 0.41702 a = 0.5 ( N b = 0.5( N aH s 有四个极点： ( ) 1 N  ) = 0.3646 1 N  ) = 1.0644 0.3P =（a c ） cos      2 8      (b c )sin      2 8     = -0.0877  j0.6179 1.2P = （a c ） cos     2  3  8     (b c ) sin     2  3  8    = -0.2117  j0.2559 因此， ( ) H s a  K  s ( 3 k  0 = 2 ( s  p k )  0.89125 0.1103 0.3895  0.4234 s  0.3895)(  s s 2 0.1754  0.1103) 分子是要使得有： aH j ( 0)  1  1 2  = 0.89125 4.2 MATLAB 的实现已知滤波器的技术要求，利用 U-chblap 函数，我们提供了一个称为 afd-chb1 的函数用于设计一个模拟切比雪夫 I 型低通滤波器。这个函数给出如后面的目录所示。为了展示模拟滤波器的频域图，我们提供的一个称为 freqs_m 的函数，它是有 MATLAB 提供的函数 freqs 的修正形式。这个函数以绝对值和相对值 dB 尺度计算幅度响应以及相位响应，在 freqs_m 函数中响应是一直要计算到最大频率 max 。freqs_m 函数见附录。这个模拟滤波器的脉冲响应 ha(t)是用 MATLAB 的 impulde 函数计算出来的。通过 MATLAB 实现的系统函数为 aH s  ( ) 2 ( s   0.89125 0.1103 0.3895  0.4234 s  0.3895)(  s s 2 0.1754  0.1103) 这个 Ha(s)与计算的结果稍有不同，这是因为在计算中用了 c =0.5，而在 asfd_butt

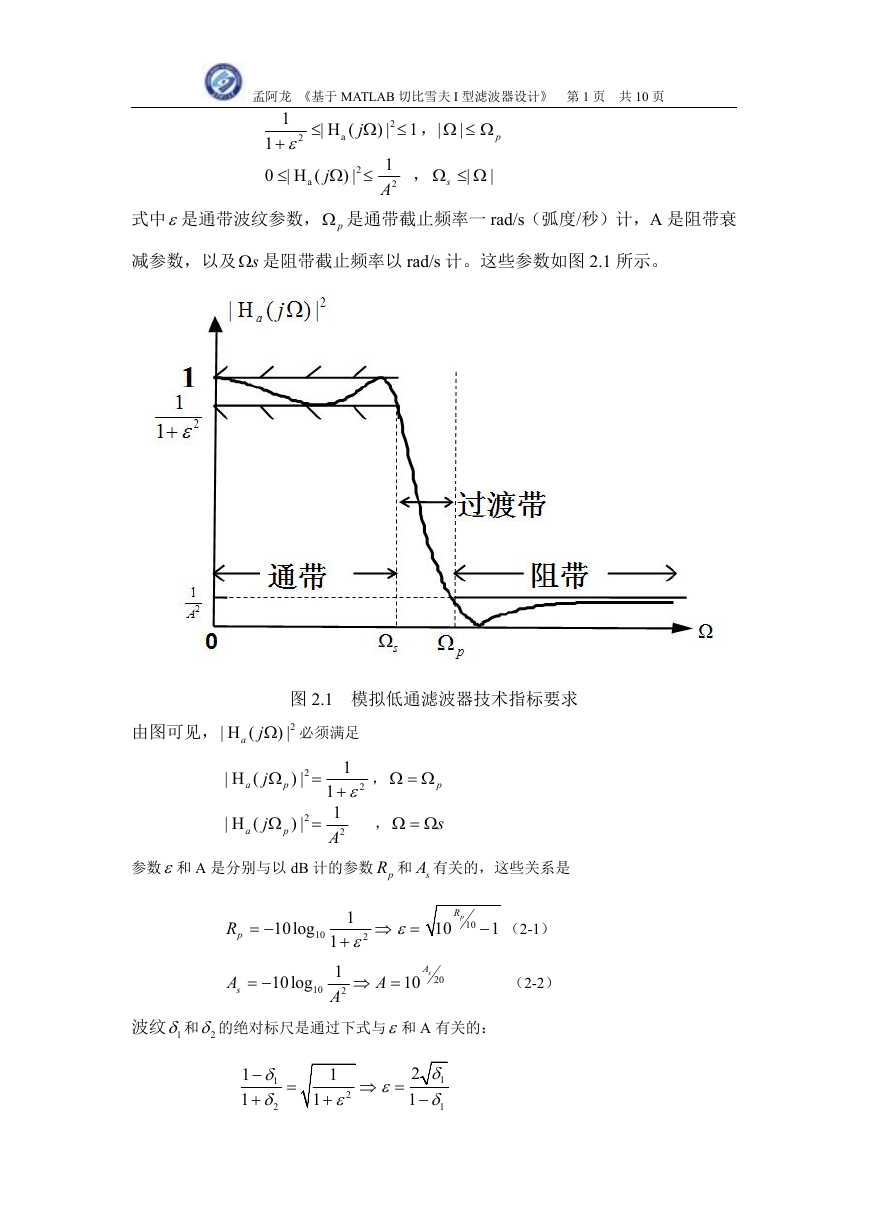
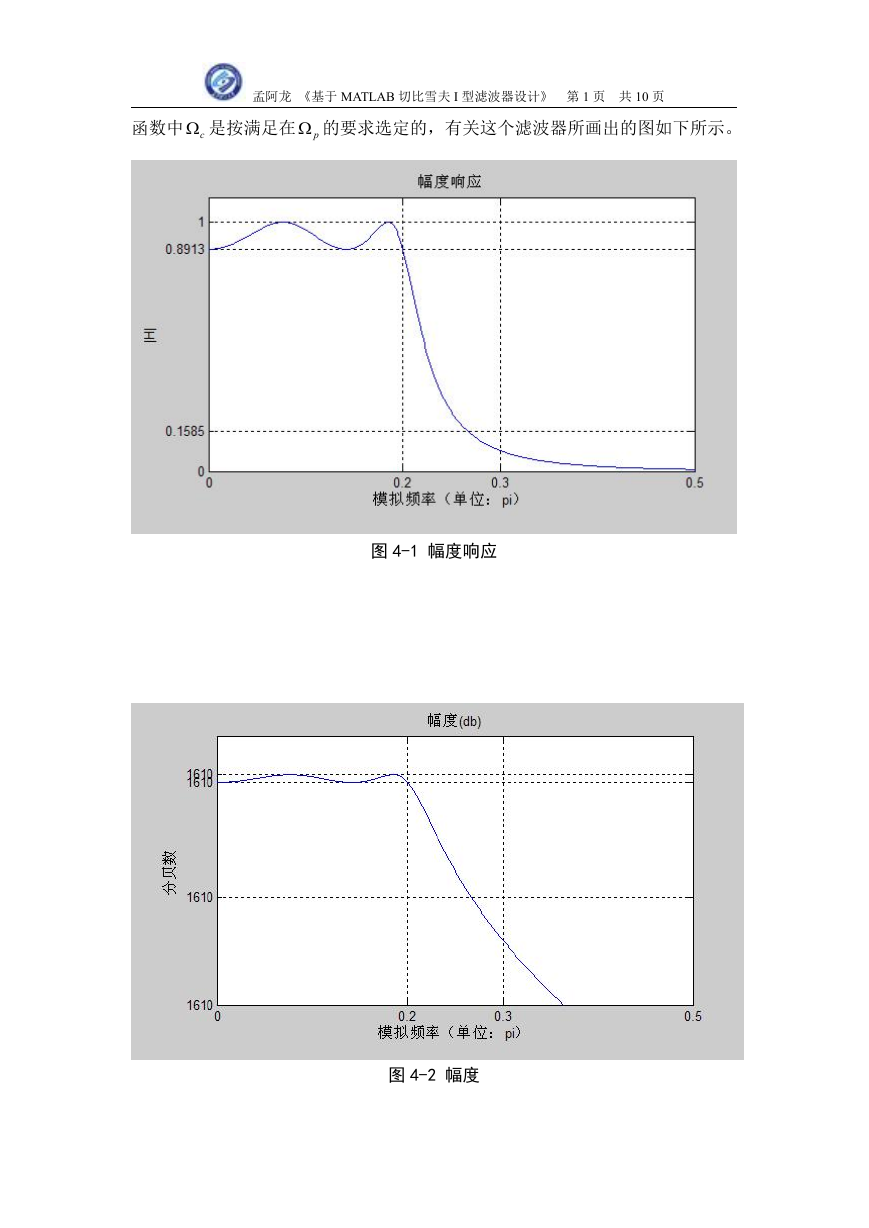
孟阿龙《基于 MATLAB 切比雪夫 I 型滤波器设计》第 1 页共 10 页函数中 c 是按满足在 p 的要求选定的，有关这个滤波器所画出的图如下所示。图 4-1 幅度响应图 4-2 幅度

资料库

基于MATLAB切比雪夫I型滤波器设计.doc

相关推荐

开发技术

热门标签

最新资料