第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
季节性时间序列建模与预测.pdf
季节性时间序列建模与预测
http://www.paper.edu.cn
孟玲清，宋学娜，王晓雨
辽宁工程技术大学理学院，阜新（123000）
E-mail ：menglingqing_99@163.com
摘 要：所谓所谓时间序列，就是各种社会、经济、自然现象的数量指标按照时间次序排
列起来的统计数据，其有多种构成因素，每种因素对系统的影响不同。本文通过分析季节
因素并建模预测。
关键词：时间序列，季节因素，建模，预测
1. 引言
很多时间序列表现出季节性特点，例如旅游人数，海滨城市在夏季旅游人数会增加许
多，再例如“十一”、“五一”、春节等节假日零售额会增加等。季节数据和月度数据经常表
现出季节性特点，即每年相同季度和月份会出现相同的特征。这种规律是由于季节（周
期）变化的原因所引起的。季节性时间序列包括平稳的和非平稳的。Box 和 Jenkins 对具有
季节性特点的数列建模方法同没有季节性的数据建模方法是一样的。在此基础上，我们进
行了建模以及预测。在模型的建立过程中需要讨论季节模型周期点的自相关和偏自相关函
数。建立完模型以后，用此模型推测未来。
2. 相关知识
2.1 时间序列的含义
从统计意义上讲，所谓时间序列就是某项统计指标按时间顺序记录的指标值数列。从
,...
1 xx
,
,...
nX
,...
是按时间次序排列的随机变量序列，
其观测值序列
数学意义上讲，时间序列的数学实质
,...
,...
为N个观测样本。时间序列
XX
,
1
XX
,
称
或 ( )tX 。从系统意义上看，
时间序列就是某一系统在不同时间地点的响应。是系统行为量化数据的有序客观记录，反
映了系统的结构特征和运行规律[1]。
一条轨迹或一次实现，轨迹片段
简记为{
}TtX t ∈,
XX
,
2
1
nX
,...
nX
,...
xx
,
1
称为
Nx
...,
,2
2
2
1
2
时间序列的构成因素：T ：趋势项，长期看时间序列逐渐增加或逐渐减少的变化。
C ：循环项，时间超过一年的周期性变动。 S ：季节项，一年内的周期性变动。 e ：随机
项，不可预测的偶然因素对时间序列的影响
随机时间序列分析就是用数学的方法描述时间序列的构成因素，具体的说就是对影响
时间序列的长期趋势、季节变动、循环波动进行测定和估计；进一步的见它们从时间序列
中分离（或删除）后，对剩余影响时间序列的随机波动进行分析和建模；从而实现对时间
序列变化规律的认识、预测或控制系统的未来行为。对循环波动测定和估计，往往更多的
依赖相关专业领域的经验和大量的样本数据。随机时间序列分析的一个主要环节就是剔除
趋势项和季节项。方法有：典型分解方法和 Box-Jenkins 方法
2
σ=
S
+
典型分解方法：
Box-Jenkins 方法：对数据{
}tX 反复作用差分算子，直至满足平稳随机过程理论建模的
(
RER
t
i
(
RE
2
t
T
i
,0
X
=
+
=
)
)
,
i
i
基本要求，然后用平稳过程理论进行分析、建模和预测。
- 1 -
2.2 随机时间序列
时间序列（随机过程的观点）：时间序列的数学本质是按时间顺序排列的随机变量序
列。
http://www.paper.edu.cn
平稳时间序列：统计过程不随时间的平移而发生改变的时间序列。分为严平稳时间序
列：随时间的平移在任意 n 个时刻的 n 维随机变量的联合分布函数不发生改变。即对任意
t
t
, 2
,...,
1
(
xxF
tx
,
;
n
n
列：数学期望 E 与协方差 R 总是存在的，并且
T
,
∈ τ
n
tx
,...,
;
n
。（宽）平稳时间序
xxF
,
n
T
∈
t
,
t
,
ττ
,
有
,...,
)τ
,...,
,...,
+
+
+
=
)
(
t
t
t
n
n
2
1
2
1
2
1
2
1
{
EX
t
(
XE
Tta
∈∀=
)(
RaXa
−+
t
τ
)
=−
t
( )
,
τ
T
τ
∈+∀
tt
,
严平稳+二阶矩存在宽平稳性，反之未必。正太时间序列严平稳性与宽平稳性相互等
价。
白噪声是最简单的平稳时间序列，记为 (
)2
,σµWN
设{ }tε 是一个平稳时间序列，并对
任意
{
ts
,2
=
σ
ts
,0
≠
有
， cov (
µε =tE
Zts ∈,
独立白噪声：白噪声序列中的各个时刻的随机变量相互独立。
正态白噪声：白噪声序列是正太时间序列。
] =
[
(
)
µεµε
εε
t
)(
E
−
−
=
)
,
s
s
t
标准白噪声：
= σµ
,0
2 =
1
2.3 时间序列的自相关性：
时间序列建模的依据是序列存在动态的自相关性，即前一时刻的随机变量与后续（一
定时限内）时刻的随机变量的自相关函数（或自协方差函数）不为零。平稳时间序列的自
相关性体现在均值是常数；自协方差函数仅与两个时刻的时差（时间推移的步长）有关，
对于固定的时差而言也是常数。白噪声序列没有自相关性[1]。
3. 应用实例
测得某地区一口井 7 年的地下水埋深数据如表一所示：
8.81
9.4
8.65
10.71 10.24 8.48
6.38
6.39
6.51
6.93
7.21
7.21
7.68
7.85
7.66
8.14
8.27
8.71
9.96 10.47
10.16
表 1 地下水埋深数据
10.01
9.88
7.14
7.82
8.53
10.43
11.7
11.07
10.31
7.26
8.57
9.38
11.47
10.1
11.54
10.53
8.49
9.59
10.09
11.73
10.37
12.73
9.55
9.39
8.77
10.59
11.6
12.47
12.43
6.51
9.71
8.61
10.83
11.93
11.91
11.64
7.75
9.65
8.94
10.49
11.55
10.83
11.1
5.96
8.84
8.35
8.66
10.85
11.39
5.21
7.8
8.29
9.26
7.95
8.4
9.21
8.39
11.35 11.11 10.49
10.64 10.29 10.34
- 2 -
http://www.paper.edu.cn
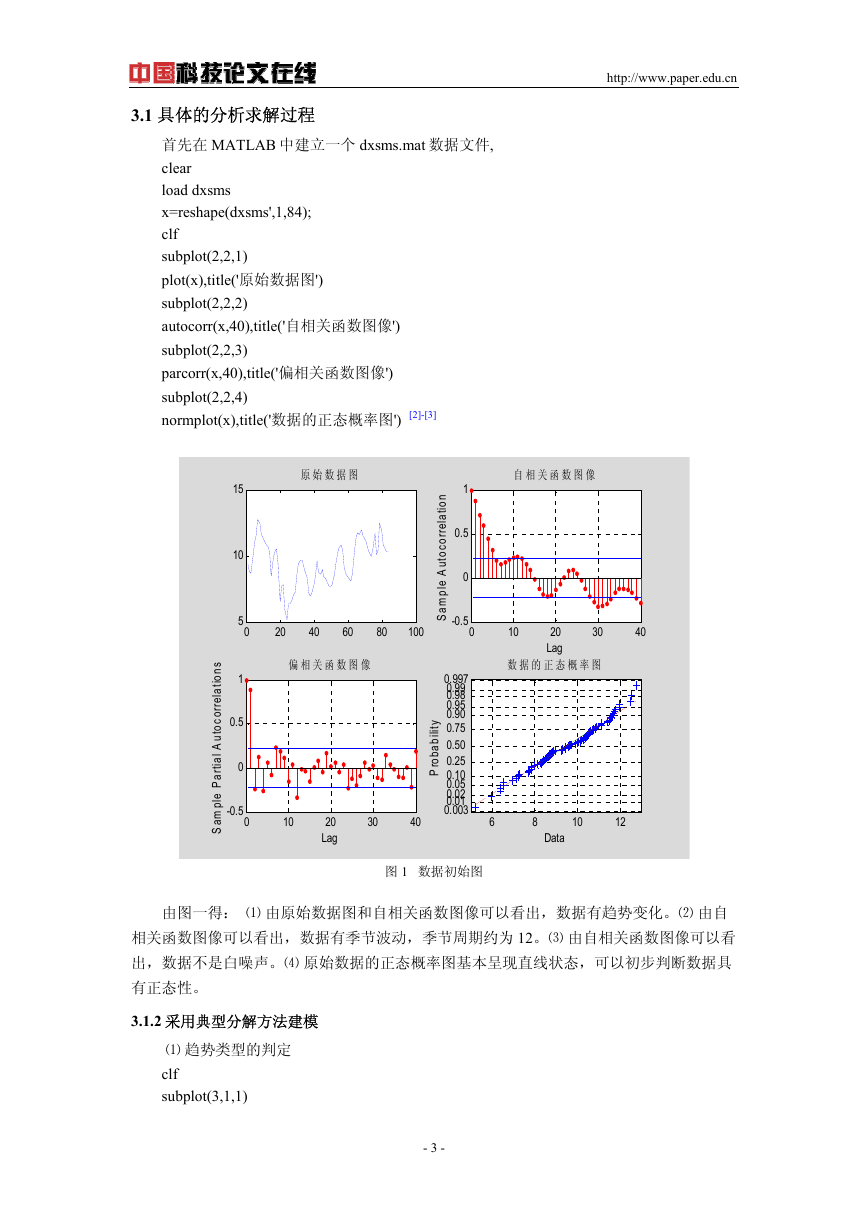
3.1 具体的分析求解过程
首先在 MATLAB 中建立一个 dxsms.mat 数据文件,
clear
load dxsms
x=reshape(dxsms',1,84);
clf
subplot(2,2,1)
plot(x),title('原始数据图')
subplot(2,2,2)
autocorr(x,40),title('自相关函数图像')
subplot(2,2,3)
parcorr(x,40),title('偏相关函数图像')
subplot(2,2,4)
normplot(x),title('数据的正态概率图') [2]-[3]
n
o
i
t
a
l
e
r
r
o
c
o
t
u
A
e
l
p
m
a
S
自 相 关 函 数 图 像
1
0.5
0
-0.5
0
10
30
40
20
Lag
0.997
0.99
0.98
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.02
0.01
0.003
y
t
i
l
i
b
a
b
o
r
P
数 据 的 正 态 概 率 图
6
8
Data
10
12
原 始 数 据 图
20
40
60
80
100
偏 相 关 函 数 图 像
15
10
5
0
1
0.5
0
-0.5
0
10
30
40
20
Lag
s
n
o
i
t
a
l
e
r
r
o
c
o
t
u
A
l
a
i
t
r
a
P
e
l
p
m
a
S
图 1 数据初始图
由图一得： ⑴ 由原始数据图和自相关函数图像可以看出，数据有趋势变化。⑵ 由自
相关函数图像可以看出，数据有季节波动，季节周期约为 12。⑶ 由自相关函数图像可以看
出，数据不是白噪声。⑷ 原始数据的正态概率图基本呈现直线状态，可以初步判断数据具
有正态性。
3.1.2 采用典型分解方法建模
⑴ 趋势类型的判定
clf
subplot(3,1,1)
- 3 -
http://www.paper.edu.cn
DETx=x(2:end)-x(1:end-1);
plot(DETx),title('一阶差分数据图')
subplot(3,1,2)
DET2x=DETx(2:end)-DETx(1:end-1);
plot(DET2x),title('二阶差分数据图')
subplot(3,1,3)
LOUx=x(2:end)./x(1:end-1);
plot(LOUx),title('一阶环比数据图') [2]-[3]
5
0
-5
0
5
0
-5
0
1.5
1
0.5
0
一阶差分数据图
10
20
30
40
50
60
70
80
90
二阶差分数据图
10
20
30
40
50
60
70
80
90
一阶环比数据图
10
20
30
40
50
60
70
80
90
图 2 差分环比图
由图得：一、二阶差分均在 0 附近波动，二阶差分比一阶差分波动幅度大，故不应拟
合二次抛物线；有趣的是一阶环比图像与一阶差分图像形态十分相似，一阶环比图像在 1
上下小幅波动，而环比为 1 的序列即是一阶差分恒等的序列.因此，可以认为序列的趋势是
线性的.
⑵ 拟合趋势 T=a+bt，剔除趋势
t=1:84;
A=[ones(84,1),t'];
aENDb=regress(x',A)
结果：aENDb =8.7620 0.0161
T=8.7620+0.0161*t;
⑶ 剔除季节影响（季节平均法）
T=[];
for t=1:84
T(t)=8.7620+0.0161*t;
- 4 -
http://www.paper.edu.cn
end
T;
x_T=x-T;
MENAx_T=mean(reshape(x-T,7,12));
S=[];
for k=1:7
S=[S,MENAx_T];
end
w=x_T-S;
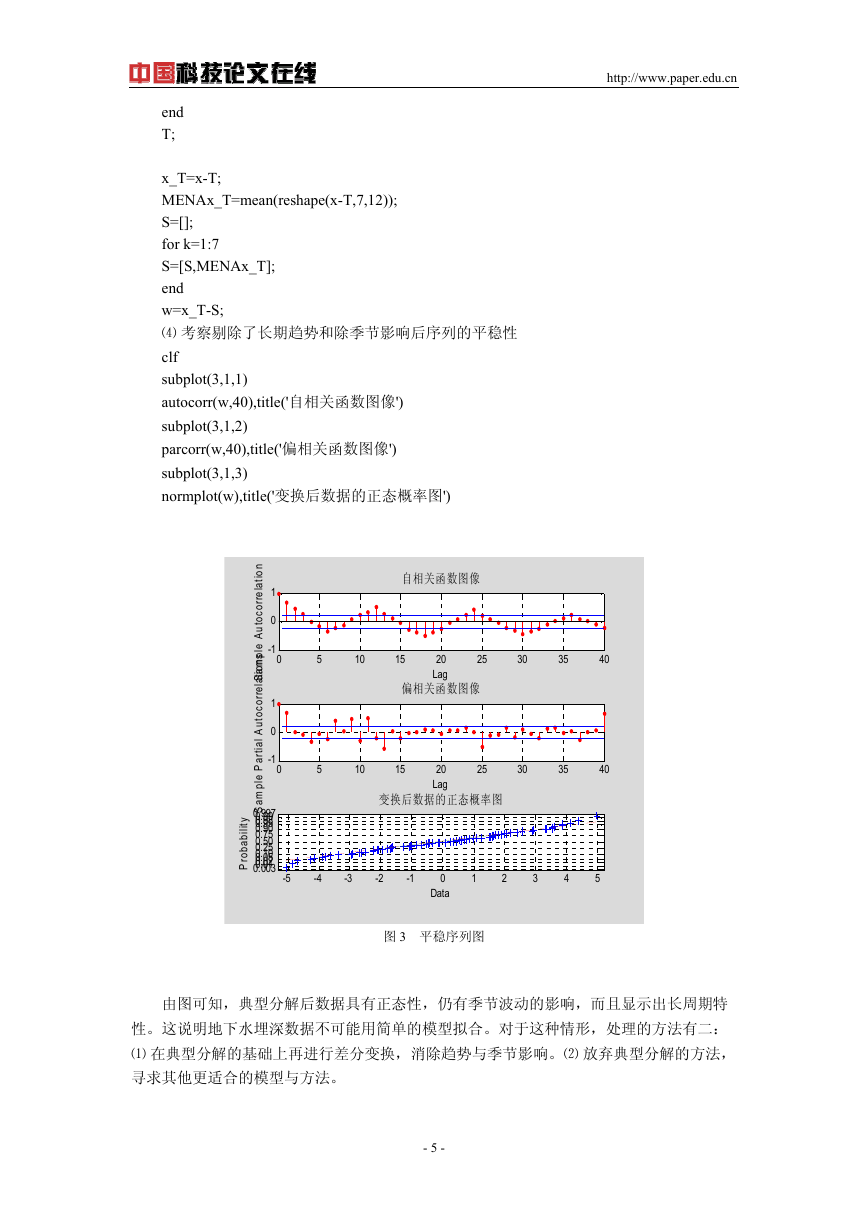
⑷ 考察剔除了长期趋势和除季节影响后序列的平稳性
clf
subplot(3,1,1)
autocorr(w,40),title('自相关函数图像')
subplot(3,1,2)
parcorr(w,40),title('偏相关函数图像')
subplot(3,1,3)
normplot(w),title('变换后数据的正态概率图')
n
o
i
t
a
l
e
r
r
o
c
o
t
u
A
e
l
p
s
n
m
o
a
S
a
i
t
l
e
r
r
o
c
o
t
u
A
l
a
i
t
r
a
P
e
l
1
0
-1
0
1
0
-1
0
5
5
自相关函数图像
10
15
20
Lag
25
30
35
40
偏相关函数图像
10
15
20
Lag
25
30
35
40
变换后数据的正态概率图
p
m
a
0.997
S
0.99
0.98
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.02
0.01
0.003
P
y
t
i
l
i
b
a
b
o
r
-5
-4
-3
-2
-1
0
Data
1
2
3
4
5
图 3 平稳序列图
由图可知，典型分解后数据具有正态性，仍有季节波动的影响，而且显示出长周期特
性。这说明地下水埋深数据不可能用简单的模型拟合。对于这种情形，处理的方法有二：
⑴ 在典型分解的基础上再进行差分变换，消除趋势与季节影响。⑵ 放弃典型分解的方法，
寻求其他更适合的模型与方法。
- 5 -
http://www.paper.edu.cn
3.1.3 采用 Box-Jenkins 方法建模
clear
load dxsms
x=reshape(dxsms',1,84);
⑴ 变换
x1=x(2:end)-x(1:end-1);
⑵ 12 变换
x2=x1(13:end)-x1(1:end-12);
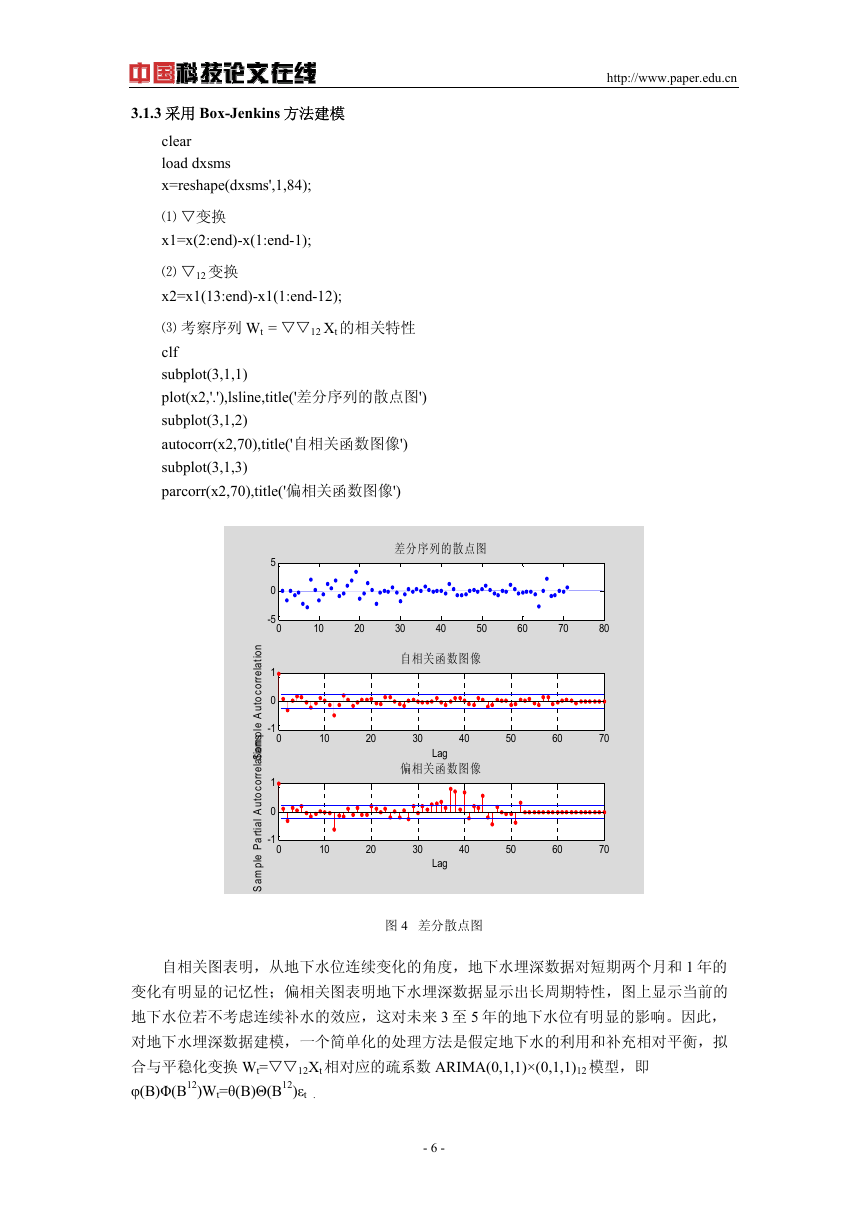
⑶ 考察序列 Wt = 12 Xt 的相关特性
clf
subplot(3,1,1)
plot(x2,'.'),lsline,title('差分序列的散点图')
subplot(3,1,2)
autocorr(x2,70),title('自相关函数图像')
subplot(3,1,3)
parcorr(x2,70),title('偏相关函数图像')
5
0
-5
0
1
0
-1
0
1
0
-1
0
n
o
i
t
a
l
e
r
r
o
c
o
t
u
A
e
l
p
s
m
n
o
a
S
a
i
t
l
e
r
r
o
c
o
t
u
A
l
a
i
t
r
a
P
e
l
p
m
a
S
差分序列的散点图
10
20
30
40
50
60
70
80
自相关函数图像
10
20
30
Lag
40
50
60
70
偏相关函数图像
10
20
30
Lag
40
50
60
70
图 4 差分散点图
自相关图表明，从地下水位连续变化的角度，地下水埋深数据对短期两个月和 1 年的
变化有明显的记忆性；偏相关图表明地下水埋深数据显示出长周期特性，图上显示当前的
地下水位若不考虑连续补水的效应，这对未来 3 至 5 年的地下水位有明显的影响。因此，
对地下水埋深数据建模，一个简单化的处理方法是假定地下水的利用和补充相对平衡，拟
合与平稳化变换 Wt=12Xt 相对应的疏系数 ARIMA(0,1,1)×(0,1,1)12 模型，即
φ(B)Φ(B12)Wt=θ(B)Θ(B12)εt .
- 6 -
http://www.paper.edu.cn
3.2 以下利用SAS系统的proc arima过程进行建模和预测
1. 下面仅利用 AIC 准则寻求最优模型的计算结果：
表 2 模型选优
序号
自回归部分阶数结
滑 动 平 均 部 分 阶 数
AIC 评价值
1
2
3
4
5
6
结构 q
构 p
p=(18)
p=(1, 2, 3, 12)
p=(1, 2, 12)
p=(1, 2, 12)
p=(1, 2, 12)
p=(1, 2, 12)
q=(12)
q=(12, 13)
q=(12)
q=(11, 12)
q=(1,11, 12, 13)
200.0904
173.3431
173.4143
173.3393
174.7314
174.9496
由 AIC 定阶准则，取 p=(1,2,12)，q=(12)，即最优模型的结构是
2. 对该模型参数进行条件最小二乘（CLS）估计，得
Wt–φ1Wt-1–φ2Wt-2–φ12Wt-12=εt–θ12εt-12
φ1=0.01501，φ2=-0.38784，φ12=-0.11895，θ12=0.82203.
3. 由 proc arima[4]-[5]过程对第 8 年全年的地下水埋深进行预报，预报值和预报标准差如下：
表 3 预报值和预报标准差
步长（月）
1
2
3
4
5
6
7
8
9
10
11
12
4. 预报结果的可视化
预报标准差
0.7928
1.1297
1.2343
1.3274
1.4579
1.5830
1.6813
1.7733
1.8662
1.9552
2.0383
2.1179
预报值
10.1417
9.6324
9.6163
10.8435
11.5519
12.0825
12.4512
12.1491
11.9308
11.5039
10.9755
10.5892
- 7 -
15
14
13
12
11
10
9
8
70
http://www.paper.edu.cn
地下水埋深预测图
75
80
85
90
95
100
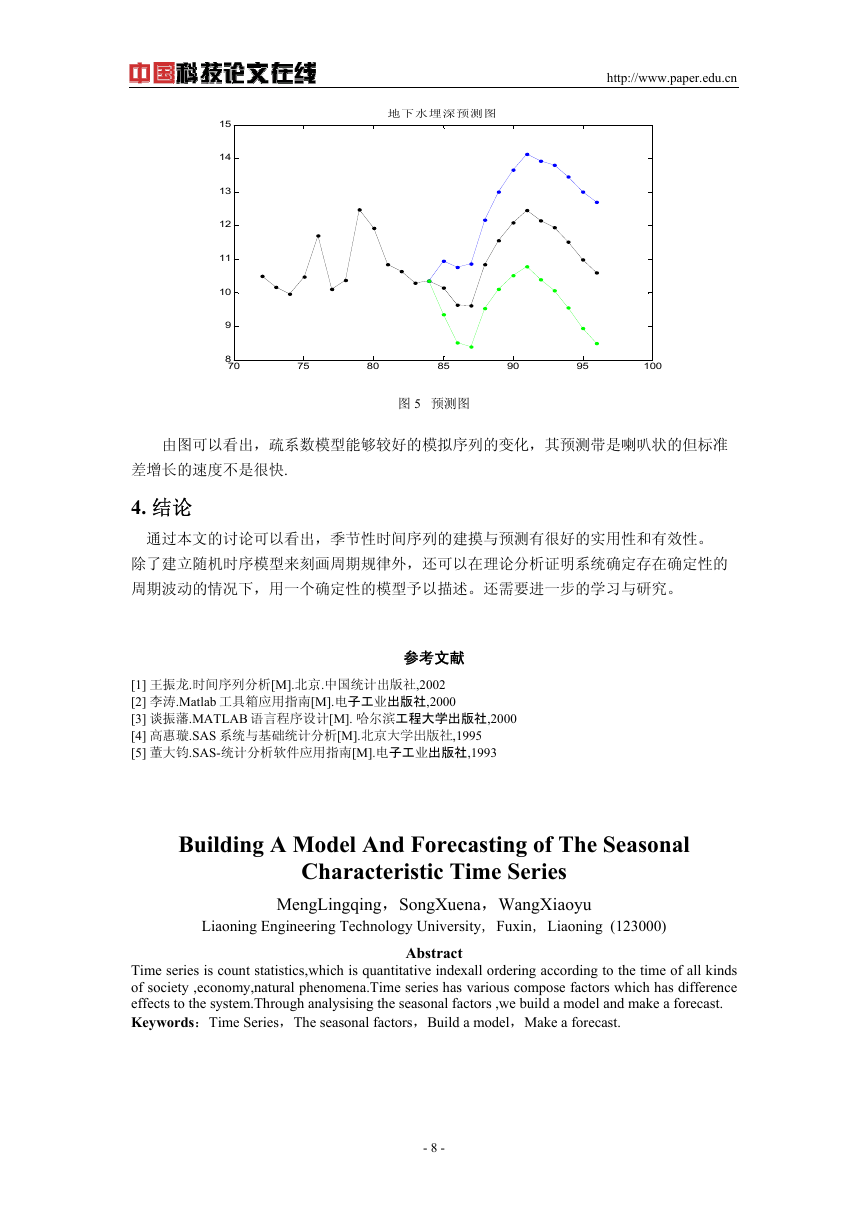
图 5 预测图
由图可以看出，疏系数模型能够较好的模拟序列的变化，其预测带是喇叭状的但标准
差增长的速度不是很快.
4. 结论
通过本文的讨论可以看出，季节性时间序列的建摸与预测有很好的实用性和有效性。
除了建立随机时序模型来刻画周期规律外，还可以在理论分析证明系统确定存在确定性的
周期波动的情况下，用一个确定性的模型予以描述。还需要进一步的学习与研究。
参考文献
[1] 王振龙.时间序列分析[M].北京.中国统计出版社,2002
[2] 李涛.Matlab 工具箱应用指南[M].电子工业出版社,2000
[3] 谈振藩.MATLAB 语言程序设计[M]. 哈尔滨工程大学出版社,2000
[4] 高惠璇.SAS 系统与基础统计分析[M].北京大学出版社,1995
[5] 董大钧.SAS-统计分析软件应用指南[M].电子工业出版社,1993
Building A Model And Forecasting of The Seasonal
Characteristic Time Series
MengLingqing，SongXuena，WangXiaoyu
Liaoning Engineering Technology University，Fuxin，Liaoning (123000)
Abstract
Time series is count statistics,which is quantitative indexall ordering according to the time of all kinds
of society ,economy,natural phenomena.Time series has various compose factors which has difference
effects to the system.Through analysising the seasonal factors ,we build a model and make a forecast.
Keywords：Time Series，The seasonal factors，Build a model，Make a forecast.
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
