logo资料库

matlab编程实现目标函数求极值的多种经典算法.doc

发布时间：2022-06-20 发布人：admin 分类：说明书 资料大小：0.38M 资料格式：doc 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    目标函数极值求解的几种方法 题目：  min 2 1 你牛顿法，共轭梯度法编程实现。 x 1 2 2   2   x  2 ，取初始点   x 1   3,1 T ，分别用最速下降法， 一维搜索法： 迭代下降算法大都具有一个共同点，这就是得到点  kx 后需要按某种规则确 定一个方向  kd ，再从  kx 出发，沿方向  kd 在直线（或射线）上求目标函数的极 小点，从而得到  kx 的后继点  1kx ，重复以上做法，直至求得问题的解，这里所 谓求目标函数在直线上的极小点，称为一维搜索。 一维搜索的方法很多，归纳起来大体可以分为两类，一类是试探法：采用这 类方法，需要按某种方式找试探点，通过一系列的试探点来确定极小点。另一类 是函数逼近法或插值法：这类方法是用某种较简单的曲线逼近本来的函数曲线， 通过求逼近函数的极小点来估计目标函数的极小点。本文采用的是第一类试探法 中的黄金分割法。原理书上有详细叙述，在这里介绍一下实现过程： ⑴ 置初始区间[ 1,ba 1 ]及精度要求 L>0,计算试探点 1 和 1 ，计算函数值 1f 和   1f ，计算公式是：  1 a 1  .0 382  b 1  1 a ，  1 a 1  .0  618 b 1  1 a 。令 k=1。 ⑵ 若 b k  a k  L 则 停 止 计 算 。 否 则 ， 当  f  >  K k f  时 , 转 步 骤 ⑶ ; 当  f    K k f  时,转步骤⑷ 。 ⑶ 置 ka 1 k , b k 1 b k , k  1 k ,  f  ,转⑸。 1k a  1  k  .0  618 b k 1   1  a k k 1  ,计算函数值 ⑷ 置 a k 1 a k , kb 1 k , k  1 k , a k  1   .0 382  b k 1   1  a k k 1  ,计算函数 值  f  ,转⑸。 1k ⑸ 置 k=k+1 返回步骤 ⑵。 1. 最速下降法 实现原理描述：在求目标函数极小值问题时,总希望从一点出发,选择一个目
    标函数值下降最快的方向,以利于尽快达到极小点,正是基于这样一种愿望提出 的最速下降法,并且经过一系列理论推导研究可知,负梯度方向为最速下降方向。 最速下降法的迭代公式是  x k  1 x  k    k d k kx 出发的搜索方 ，其中  kd 是从   xf  xf 。 k 是从  k  k d  。  k    向，这里取在点  kx 处最速下降方向，即  d  k  kx 出发沿方向  kd  进行的一维搜索步长，满足  xf  k   k d  k    实现步骤如下： min 0  ⑴ 给定初点   x 1 nR ，允许误差 0 ，置 k=1。 ⑵ 计算搜索方向  d  k   xf k 。 ⑶ 若   kd  索，求 k ，使  xf  k kx 出发，沿方向  ，则停止计算；否则，从  k  xf d  。   d   k k        k min 0  kd 进行的一维搜 ⑷  x k  1 x  k   k  k d ，置 k=k+1 返回步骤 ⑵。 2. 拟牛顿法 基本思想是用不包括二阶导数的矩阵近似牛顿法中的 Hesse 矩阵的逆矩阵， 因构造近似矩阵的方法不同，因而出现了不同的拟牛顿法。 牛 顿 法 迭 代 公 式 ：  x k  1 x  k   k  k d ，  kd 是 在 点  kx 处 的 牛 顿 方 向 ，  k  d  2  xf  k  1   xf   k  ， k 是从  kx 出发沿牛顿方向  kd 进行搜索的最优步长。 用 不 包 括 二 阶 导 数 的 矩 阵 kH 近 似 取 代 牛 顿 法 中 的 Hesse 矩 阵 的 逆 矩 阵 2    kxf    1 ， 1kH 需满足拟牛顿条件。 实现步骤： ⑴ 给定初点  1x ，允许误差 0 。 ⑵ 置 nIH 1 （单位矩阵），计算出在  1x 处的梯度 g  1  xf   1 ，置 k=1。 ⑶ 令  d  k  gH k k 。 kx 出 发 沿 方 向  kd 搜 索 ， 求 步 长 k ， 使 它 满 足 ⑷ 从   ，令  x  xf  1 k d  。    d d x k k k k k            k  xf  k  k min 0 
     ⑸ 检验是否满足收敛标准，若  1kyf    ，则停止迭代，得到点  x   kx 1 ， 否则进行步骤⑹。 ⑹ 若 k=n，令   1 x ⑺ 令 g   1 k 1    kx  1 xf  k   ，返回⑵；否则进行步骤⑺。 ，  p  k  x  k 1   k  x ，  q  k  g  g k k 1 ， H 1 k H k   k   pp   Tk q p  Tk  k       Tk k HqqH k  k qHq k  Tk  k ，置 k=k+1 。返回⑶。 3. 共轭梯度法 若   1 d , d   2 ,  ,  kd 是 nR 中 k 个 方 向 ， 它 们 两 两 关 于 A 共 轭 ， 即 满 足   Ti d Ad   j  ,0 i  ,; ij j ,1  , k ，称这组方向为 A 的 k 个共轭方向。共轭梯度法的 基本思想是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方 向，并沿这组方向进行搜索，求出目标函数的极小点，根据共轭方向的基本性质 这种方法具有二次终止性。 实现步骤如下： ⑴ 给定初点  1x ，允许误差 0 ，置  yf   1  1  ，k=j=1。 y  ，     1 1 x d   jyf ⑵ 若  ，则停止计算；否则，作一维搜索，求 j ，满足  ，令  y  yf  yf  1 j d  。    d d y j   j  j  j    j     j   j  j min 0  ⑶ 若 n j  ，则进行步骤⑷，否则进行步骤⑸ ⑷ 令  d j 1     yf  j 1     j  j d ，其中  j     yf  yf  j 1    j 2    2 ，置 j=j+1，转⑵。 ⑸ 令  x k   1   n y 1  ，   1 y   kx 1  ，   1 d   yf   1 ，置 j=1，k=k+1，转⑵ 。 4. 实验结果
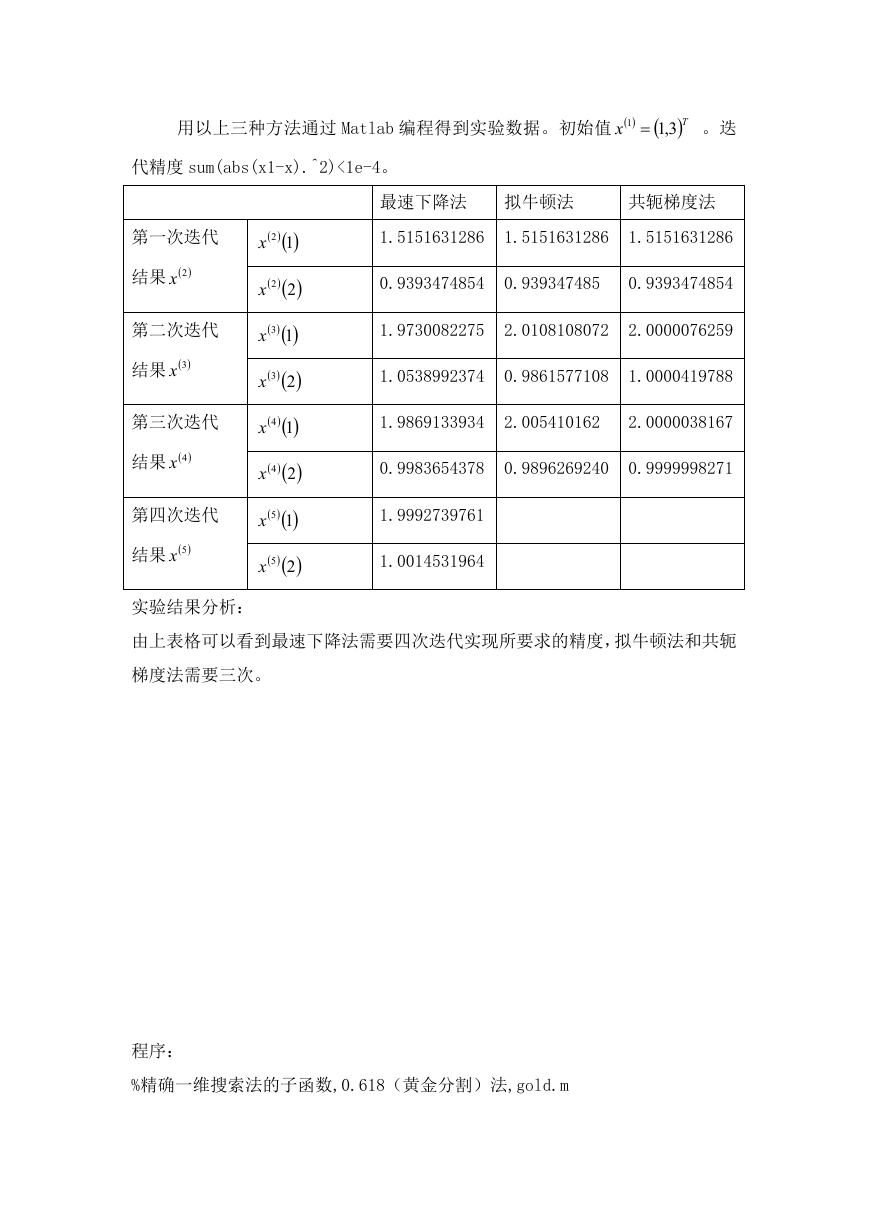
    用以上三种方法通过 Matlab 编程得到实验数据。初始值   x 1   3,1 T 。迭 代精度 sum(abs(x1-x).^2)<1e-4。 第一次迭代 结果  2x 第二次迭代 结果  3x 第三次迭代 结果  4x 第四次迭代 结果  5x   12x   22x   13x   23x   14x   24x   15x   25x 实验结果分析： 最速下降法 拟牛顿法 共轭梯度法 1.5151631286 1.5151631286 1.5151631286 0.9393474854 0.939347485 0.9393474854 1.9730082275 2.0108108072 2.0000076259 1.0538992374 0.9861577108 1.0000419788 1.9869133934 2.005410162 2.0000038167 0.9983654378 0.9896269240 0.9999998271 1.9992739761 1.0014531964 由上表格可以看到最速下降法需要四次迭代实现所要求的精度，拟牛顿法和共轭 梯度法需要三次。 程序： %精确一维搜索法的子函数,0.618（黄金分割）法,gold.m
    %输入的变量 x 为初始迭代点是二维的向量,d 为初始迭代方向是二维的向量 %输出变量是在[0,10]区间上使函数取得极小值点的步长因子 function alfa=gold(x,d) a=0;b=10;tao=0.618; lanmda=a+(1-tao)*(b-a); mu=a+tao*(b-a);alfa=lanmda;%初始化 f=((x(1)+alfa*d(1))-2)^2+2*(x(2)+alfa*d(2)-1)^2;%目标函数 m=f;alfa=mu;n=f; while 1 if m>n if abs(lanmda-b)<1e-4 alfa=mu; return else a=lanmda; lanmda=mu; m=n; mu=a+tao*(b-a); alfa=mu; n=((x(1)+alfa*d(1))-2)^2+2*(x(2)+alfa*d(2)-1)^2; end else if abs(mu-a)<1e-4 alfa=lanmda; return else b=mu; mu=lanmda; n=m; lanmda=a+(1-tao)*(b-a); alfa=lanmda; m=((x(1)+alfa*d(1))-2)^2+2*(x(2)+alfa*d(2)-1)^2; end end end %梯度子函数，tidu.m,输入的变量为二维的向量，返回梯度在 x 处的数值向量 function g=tidu(x)
    %待求解的函数 f=(x(1)-2)^2+2*(x(2)-1)^2; %求函数的梯度表达式 g=[2*(x(1)-2) 4*(x(2)-1)]; x1=x(1); x2=x(2); %最速下降法极小化函数的通用子函数 zuisu.m %输入变量为初始的迭代点，输出变量为极小值点 function x0=zuisu(x) %判断梯度范数是否满足计算精度 1e-4 的要求.是,标志变量设为 1，输出结果; %否,标志变量设为 0 if sum(abs(tidu(x)).^2)<1e-4 flag=1; x0=x; else end flag=0; %循环求解函数的极小点 while flag==0 d=-tidu(x); a=gold(x,d); x=x+a*d %判断梯度范数是否满足计算精度的要求.是,标志变量设为 1，输出结果; %否,标志变量设为 0，继续迭代 if sum(abs(tidu(x)).^2)<1e-4 flag=1; x0=x; else end flag=0; End %拟牛顿法极小化函数的通用子函数，gonge.m %输入变量为初始的迭代点，输出变量为极小值点
    function x0=ninewton(x) %判断梯度范数是否满足计算精度的要求.是,标志变量设为 1，输出结果; %否,标志变量设为 0，继续迭代 if sum(abs(tidu(x)).^2)<1e-4 flag=1； x0=x; else end flag=0; %初始的 H 矩阵为单位矩阵 h0=eye(2); %循环求解函数的极小点 while flag==0 %计算新的迭代方向 d=-h0*tidu(x)'; a=gold(x,d); x1=(x'+a*h0*d)'; s=x1-x; y=tidu(x1)-tidu(x); v=s*y'; %校正 H 矩阵 h0=(eye(2)-s'*y./v)*h0*(eye(2)-y'*s./v)+s'*s./v; %判断下一次和上一次迭代点之差是否满足计算精度的要求.是,标志变量设 为 1，输出结果;否,标志变量设为 0，继续迭代 if sum(abs(x-x1).^2)<1e-4 flag=1; x0=x; else flag=0; end x=x1 end %共轭剃度法极小化函数的通用子函数，gonge.m %输入变量为初始的迭代点，输出变量为极小值点
    function x0=gonge(x) %判断梯度范数是否满足计算精度的要求.是,标志变量设为 1，输出结果; %否,标志变量设为 0，继续迭代 if sum(abs(tidu(x)).^2)<1e-4 flag=1; x0=x; else end flag=0; %第一次的迭代方法为负梯度方向 d1=-tidu(x);a=gold(x,d1);x1=x+a*d1; %循环求解函数的极小点 while flag==0 g1=tidu(x); g2=tidu(x1); %利用 FR 公式求解系数 bata bata=(g2*g2')/(g1*g1'); d2=-g2+bata*d1; a=gold(x1,d2); x=x1; x1=x+a*d2 %判断下一次和上一次迭代点之差是否满足计算精度的要求.是,标志变量设 为 1，输出结果;否,标志变量设为 0，继续迭代 if sum(abs(x1-x).^2)<1e-4 flag=1; x0=x1; else flag=0; end end
    分享到：
    赞 收藏

    相关推荐

    资料库

    大数据

    共收录841份资料，累计11个分类，关注成员有19位，主要包括：Matlab,统计分析,数据挖掘,Hbase,Hive,flink,kafka,spark,Storm,算法与数据结构,Hadoop

    热门标签

    Matlab 统计分析 数据挖掘 Hbase Hive flink kafka spark Storm 算法与数据结构 Hadoop

    最新资料