第 12 卷第 5 期 2011 年 10 月 信 息 工 程 大 学 学 报 Journal of Information Engineering University Vol. 12 No. 5 Oct. 2011 基于组合 移位的指数运算 - FPGA 实现方法 吉立新，魏开容，刘冰洋，聂智良 ( 信息工程大学 信息工程学院，河南 郑州 ) 450002 摘要: 针对 FPGA 实现指数运算时， CORDIC 方法计算范围小而多项式逼近需要较多乘法器的 问题，设计了一种基于组合-移位的指数运算 FPGA 实现方法。通过对查找表中元素的线性组 合逼近自变量，将其映射为对应指数函数值的相乘( 加减移位) ，实现准确的指数运算。仿真 结果表明，该指数运算的 FPGA 实现方法以较少的资源占用保证了指数运算的精度和速度，取 得了良好的实现效果。 关键词: FPGA 实现; 指数运算; 组合; 移位 中图分类号: TN402 文献标识码: A 文章编号: 1671 － 0673 05 － 0569 － 05 2011 ( ) FPGA Implementation of Exponentiation Computation Based on Combination-Shifting ， JI Li-xin WEI Kai-rong ， LIU Bing-yang ， NIE Zhi-liang ( : Institute of Information Engineering Information Engineering University Zhengzhou 450002 ， ， ， ， China ) Abstract In FPGA implementation of exponential functions the CORDIC method is not enough and the number of multipliers reguired by polynomial approximation is large． This paper suggests a FPGA implementation method of combination-shifting exponentiation computation． By the selection and combination of sequence elements for index domain the deductions shift was mapped to realize ac- ， curate exponentiation computation． Simulation results show that this FPGA implementation of expo- nentiation computation costs less to ensure the accuracy and speed of exponentiation compatation． FPGA implementation exponentiation computation combination shifting ; ; ; : Key words 引言 0 CORDIC 限的 实际工程应用中，常常需要进行指数运算的 实现方法［ 1-2 ］ 查表法和多项式逼近［ 、 实现 指数函数 FPGA 。 ( f ) x = e － x， x≥0 ］等方法进行电路实现 3 在精度要求相对较高 的运算可以采用 硬件资源受 、 。 FPGA CORDIC 的环境下，上述几种方法存在资源占用比较大的不足 年 算法最早由 于 。 从而能够计算指数函数 查表法可以应用于指数函数的 核实现 精度要求比较高的情况下，查找表较大 方法，但当多项式逼近次数较高时，则需要使用较多的乘法器 CORDIC 。 。 1971 1959 Walther 年提出， 将 实现方法采用双曲线模式［ 实现，然而指数函数在 FPGA 分段多项式逼近实现方法［ J． D． Volder 指数运算的 。 算法拓展至双曲坐标， CORDIC ］，其运算可以使用 4 CORDIC IP 轴的取值范围比较大，所以在运算 实现一种常用 为此本文利用实际工程应用当中需要实现 x ］也是指数运算 FPGA 5 。 收稿日期: 2011-04-26; 修回日期: 2011-06-29 基金项目: 国家 863 作者简介: 吉立新( 魏开容( 计划资助项目( 1969 － 1980 － 2011AA010603 ) ) ，男，研究生，硕士生导师，主要研究方向为通信网信息安全; ) ，男，硕士生，主要研究方向为自动语言辨识 设计 、FPGA 。 

570 信 息 工 程 大 学 学 报 年 2011 的指数运算 ( f ) x = e － x， x≥0 区间比较特殊，设计了一种基于组合 移位的指数运算 - FPGA 实现方法 。 组合 移位指数运算实现方法 - 1 在 FPGA 设计当中，加减移位运算的资源开销要小于乘除运算，所以如果指数运算的 实现使用 观察指数运算的性质可知: 一个数如果是一组序列元素的和，那么其 加减移位实现将可以节省资源开销 指数函数值就是这些序列元素指数函数值的积，而如果这个积的过程适合使用加减移位来实现，那么就可 以达到减小资源开销的目的 FPGA 。 下面对本文 组合 “ ” 。 移位 式中，由 ， x2 ， x3 ， … ， xn x1 只需加减移位就能实现，那么指数运算的 与 “ 的概念进行描述，指数函数 ( x f ” y = e － x = e － x1 e － x2 e － x3 …e － xn， ∑n 所构成的序列称为指数运算的组合序列 ) = e － x， x≥0 具有如下性质: ) 如果组合序列对应的指数函数值相乘 1 ( i = 1 xi = x 。 FPGA 实现将非常简便，比如 1 16 × 1 4 × 1 2 × 1 －( )1 4 等，所以乘积 移位 ”。 e － x1 e － x2 e － x3 …e － xn的实现过程称为 “ 1． 1 组合与移位实现方法描述 1． 1． 1 组合序列的构建 有 1 － 1 /2 n( 构建组合序列需要列举适合的 1 /22 n， ① 为自然数) 等 列举适合加减移位实现的 计算其对应的 n xi。 ② 同时计算 xi 出定点化的序列 的元素 N ，如表 ni 1。 表 1 中 xi 计算如下: ，使得它们的乘积适合转化成加减移位，满足这样要求的 表达式 yi yi 找到 。 xi yi = e － xi， yi∈ ( ) ; ， 1 0 的组合序列需要一个步骤: 对应的定点数值，令定标为 Q32． 23 ，定点化函数 ［ e － xfix /2 f yfix = × 2 f］， xfix = 0 ， 1 ， 2 ， …。 求 { xi = － log ( xi = log 1 － 1 /2 j) ， j = 23 ， ， ， 1 2 3 k = 0 ( 22 k) ， 。 ( ) 3 3 ni 通过公式( ) 计算，其中符号［］为取整 ［ xi × 223］ 1． 1． 2 组合-移位实现方法 ni = 利用构建好的组合序列实现指数运算需要使用 组合 “ 和 ” “ 移位 两个步骤 ” 。 令未知变量为 xfix ，指数函数值为 ， 22 ， 21 ， … ， 2 ; i = 24 － j ; i = 23 + k 表 1 指数函数特殊点定点化的序列 yi xi ni -log … 1-1 /223 ( 1-1 /223 ) … -log 1 ，使用表 中 … 1 ni 1-1 /22 ( 1-1 /22 ) 2413252 的线性组合逼近 ( ) 2 ) … … 1 /2 ( 2 log 5814539 … xfix。 ( 4 执行由表 ) 1 yfix ， ai = 0 or 1 的值为 0 令 初始值为 yfix 1 定义的加减移位，否则保持不变 yfix 所以基于组合移位的指数运算实现方法一个步骤描述如下: ai 4 1 1 或 ，如果为 则 所对应的定点数值，在公式( xfix≈a1 n1 + a2 n2 + … + a26 n26 ) 中找到 使用存储序列 使用这些线性组合所对应的指数函数值 ni N 。 中的元素 ① ② yi 进行线性组合使其接近给定的 值; xfix 使用组合 假设 移位实现函数 - 恰好等于 y = e － x， ( + log 4 ) x≥0 ( 4 /3 的过程举例如表 ) = 1． 6740 log x 所示 。 2 ，那么指数函数 值即为 ( y = exp － 1． 6740 ) = 1 × × 1 －( )1 4 1 4 = 0． 1875 ( ) 5 yi xi 公式( ) 硬件实现只要移位和加减就可以完成 5 。 进行乘法运算( 加减移位) ，从而近似得到函数值 yfix。 表 2 适合指数域加减移位运算的数 … 1 /4 ( ) … log 4 1 /2 ( ) log 2 ( 1-1 /4 ( 4 /3 log ) ) … … 1． 2 组合序列的约束条件 前一节举例说明，当 他值可以通过组合 移位实现指数函数值的计算 - 。 x = 1． 6740 时指数函数值可以使用加减移位来实现，但是却无法证明 或其 所以本节通过研究组合序列构建的约束条件讨论这个 x = 2 

第 5 期 吉立新等: 基于组合 移位的指数运算 - FPGA 实现方法 571 在定点数表示的情况下，固定序列 可以列举所有数轴上的值，如图 N 表示一个线性序列的组合 1 问题 范围 。 。 图 中， 8 1 以内的所有自然数可以通过 的线性 以内的所有自然数可以使用 ， 2 ， 4 1 组合表示出来; 以此类推， 32 ， 2 ， 16 1 。 线性组合表示出来等等 ， ， 8 4 如果序列线性组合构成的空间可以涵盖所有的小于 的自然数，那么可以通过公式( 的值， ) 计算出各个 ∑ni 再通过形如公式的计算就可以精确计算出指数函数值 所以组合序列精确实现指数运算的约束条件是: 序列元素 1． 3 误差分析 。 ai 4 的线性相加涵盖所有的小于 的自然数 。 ∑ni ni 对于表 1 的组合序列，序列元素 如果序列元素 的实现过程来证明 只有定点数的截断误差，其误差较小; 如果序列元素 数运算的实现过程误差相对较大 。 ni 的线性组合是否涵盖所有的小于 ni 的线性组合涵盖所有小于 ni 的自然数可以通过指数函数 的自然数，那么指数函数的实现误差 的线性组合在数轴上排列的间隔比较大，那么其指 ∑ni ∑ni 指数函数 y = e － x， 如果精度要求为 是一条单调递减趋向于 的 x≥0 0 10 － 7 量级，那么函数近似的上限 z 。 函数 满足关系: 。 故令上限 z≥ － log 通过表 所示 z = 17。 ，其误差如图 图 。 中，最大误差约为 1 2 ＜ 17 ( 10 － 7) 的组合序列实现 = 16． 12 ( ) 6 y = e － x， 0 ≤x 1 2 0． 08 要求，证明表 的自然数，并且其序列元素 ，误差远远不能满足精度 形成的线性组合空间没有涵盖所有的小于 的线性组合在数轴上排 ) 线性组合无法表 对于实际工程实现， ni ( 1、2、5 以内的所有自然数，比如数 ∑ni 列的间隔比较大，比如序列 示出 减小误差的一个办法就是对该序列增加一些重复的元素，比如增加序列元素 ) 可以表示 对于表 以内的所有自然数 的序列元素，依次增加重复元素的效果如图 ∑ = 8 4。 。 图 8 9 2 9 3。 1 指数运算算法调整前绝对误差 ，即使得序列 1 ， 1 ， 2 ， 5 ( 1 ∑ = 图 3 增加重复元素误差效果图 由图 可以看出，增加重复元素 3 ( 1 － 1 /23 ) 的效果最为明显，所以把 － log － log 个重复元素 ( ) ) 27 － 1 为增加的一个重复元素; 依次进行这样的测试最终可以筛选出来 ( ( 27 / 期，而其误差得到了很大改善，计算误差如图 可知，其最大绝对误差不超过数 23 － 1 4 1 × 10 － 7，符合精度要求 ) ) ，其 26 － 1 ) ) 和 由图 所示 FPGA 、log 26 / 23 / log 。 4 ( ( ( 4 实现时指数运算的时延增加了 ( 1 － 1 /23 ) 筛选出来作 ( 、log log 个时钟周 215 － 1 215 / ) ) ( 4 而且其包络近似为函数 。 ( f ) x = 10 － 7 e － x， x≥0。 定点环境中的误差往往会因为数据的截断处理而导致误差增大，使用 VC + + 6． 0 进行 C 定点仿真，结 

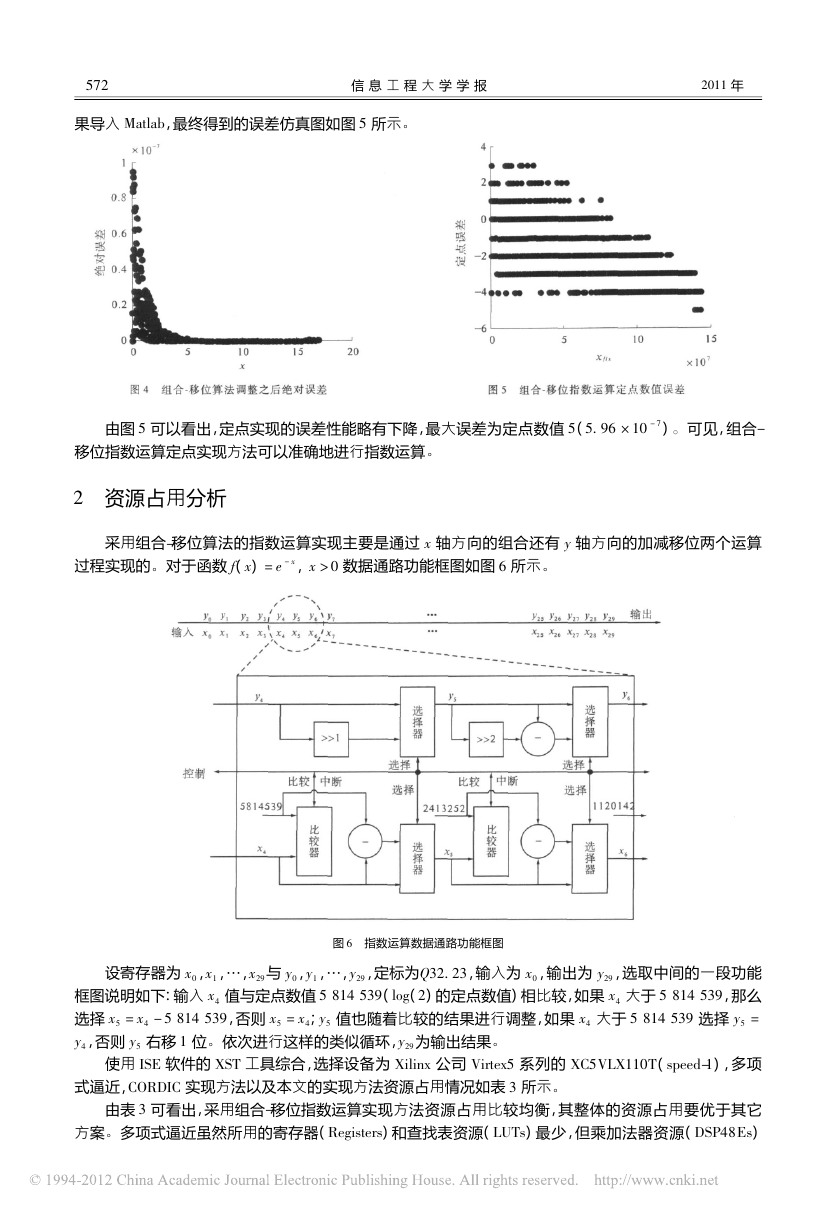
572 信 息 工 程 大 学 学 报 年 2011 果导入 Matlab ，最终得到的误差仿真图如图 所示 。 5 由图 可以看出，定点实现的误差性能略有下降，最大误差为定点数值 5 移位指数运算定点实现方法可以准确地进行指数运算 。 资源占用分析 2 采用组合 过程实现的 。 移位算法的指数运算实现主要是通过 - 对于函数 ( ) = e － x， x ＞ 0 f x x 数据通路功能框图如图 轴方向的组合还有 所示 。 6 ( 5． 96 × 10 － 7 ) 5 。 可见，组合 - 轴方向的加减移位两个运算 y 6 ， y29 设寄存器为 x0 框图说明如下: 输入 选择 ， x1 x4 x5 = x4 － 5 814 539 。 ，否则 右移 1 位 软件的 y0 与 ， … ， x29 5 814 539 ，定标为 ( ， ， y1 … 值与定点数值 ，否则 ; 依次进行这样的类似循环， y29 Xilinx 工具综合，选择设备为 x5 = x4 log y5 2 ( XST ISE 图 指数运算数据通路功能框图 ，输入为 ，输出为 x0 y29 Q32． 23 ) 的定点数值) 相比较，如果 x4 大于 值也随着比较的结果进行调整，如果 ，选取中间的一段功能 ，那么 大于 5 814 539 选择 5 814 539 y5 = x4 y4 y5 使用 式逼近， 由表 3 方案 。 实现方法以及本文的实现方法资源占用情况如表 CORDIC 可看出，采用组合 多项式逼近虽然所用的寄存器( 移位指数运算实现方法资源占用比较均衡，其整体的资源占用要优于其它 - ) ) 最少，但乘加法器资源( ) 和查找表资源( Registers LUTs DSP48Es 为输出结果 。 公司 Virtex5 系列的 所示 。 3 XC5VLX110T ( speed-1 ) ，多项 

第 5 期 吉立新等: 基于组合 移位的指数运算 - FPGA 实现方法 573 占用比较大; 体的资源占用要高; 可见，采用组合 现方法可以有效的节省资源开销 实现方法相比本文实现方法整 移位指数运算实 - CORDIC 。 结束语 3 指数运算具有性质 ea + b = eaeb，而如果等式右边的 表 3 指数运算实现方法资源占用情况 资源占用 多项式逼近 CORDIC 本文实现方法 Registers LUTs DSP48Es RAM / FIFO 199 106 4 1 1080 1058 1 — 422 778 0 — Max Freq 211． 551 296． 551 398． 698 基于指数运算的 实现组合 实现 仿真测试表明，本文提出的指数运算实现方法以较少的资源占用，保证了指数运算的精度和速 乘积过程适合使用加减移位来实现，那么就可以减小指数运算 性质，本文设计了一种组合 序列构建的约束条件，然后进行误差分析，采用增加重复元素的办法，有效的控制了指数运算 的误差 度，取得了良好的实现效果 。 移位指数运算实现方法，针对实际工程应用，分析了指数运算 - 实现的资源占用 FPGA FPGA FPGA 。 。 参考文献: ． ［ ］ 谈宜育，卞文兵，李元 1 ［ ］ 季中恒，宋博 2 ［ ］ 3 ［ ］ 胡彬 4 ［ ］ 张丰德 5 Jeffery J Leader． ． Matlab ． CORDIC CORDIC 算法的坐标变换电路［ ］ J ． 弹箭与制导学报， 一种基于 ］ 算法及其硬件实现［ J ． 2005 ］ 张威，刘志军，李艳红，译 ． 开发指南 逻辑设计篇［ M ． ］ ． — 数值分析与科学计算［ M 数值分析与应用［ M ］ ． 北京: 国防工业出版社， 2009． ． Xilinx ISE Design Suite 10． x FPGA 数据采集与处理， ( ， 16 ) : 257-260． 2 2001 ( 3 ) : 609-610． ， 25 北京: 清华大学出版社， 北京: 人民邮电出版社， : 448-449． 2008 2008． 欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍欍 ( 上接第 568 页) 算法 M＆M 、L＆R 修正算法和 FF ML 线性内插法 次方闭环 、Q 精同步，对上述算法进行了理论分析和仿真验证，同时在不考虑信道编码时，就 、 修正算法相结合能够有效的进行载频同步; 算法和 NDA 算法分别进行载波频率 信号 修正算 线性内插算法进行载波相位粗 16APSK L＆R 和相位的粗 进行了载波恢复 法进行载波频率精同步时，至少需要 同步时，估计误差趋于 结论如下: M＆M 。 ; 3° C － 4Q － DD 1000 L＆R 个导频块算法才能收敛; FF ML 算法的相位精同步曲线逼近理想同步曲线 。 ［ ］ C 结束语 4 本文采用 参考文献: ［ ］ 1 Park J W ， Systems． 2007 645-650． ， : 10 ， Casini E De Gaudenzi R． DVB-S2 mdem algorithms design and performance over typical satellite channels Int． J． The Second Generation Standard for Satellite Broad-band Services IEEE ］ ［ J ． ］ ［ J ． Sunwoo M H． An Efficient Data-Aided Initial Frequency Synchronizer for DVB-S2 / / IEEE Signal Processing De Gaudenzi R Guillen i Fabregas A． Performance Analysis of Turbo-coded APSK Modulations over Nonlinear Satellite Chan- ［ ］ 2 ［ ］ 3 ［ ］ 4 ［ ］ 5 ［ ］ 6 ， 2006 ， 5 ( 9 ) : 2396-2407． ［ ］ J nels ． IEEE Trans． On Wireless Communications ， Satell． Commun． Network 2004 22 3 281-318． ， ， ( ) : ， Alberto Morello ， Proceedings 2006 ， De Gaudenzi R ［ ］ J PSK signals : Vittoria Mignone． DVB-S2 ， ( 94 210-227． ) : 1 ， ． IEEE Communications ， 1995 ， ( ) : 43 12 3090-3100． ， Garde T Vanghi V． Performance analysis of decision-directed Maximum-Likelihood phase estimator for M- ETSI EN 302 307 v1． 2． 1 Second Generation Framing Structure Channel Coding and Modulation System for Broadcasting ， ter-active Services News Gathering and other Broadband Satellite Applications DVB-S2 ［ ］ 王华，武楠，韩存涛，等 7 ［ ］ 季仲梅，杨洪生，王大鸣，等 8 ． ］ 载波恢复算法研究［ J ． 通信中的同步技术及应用［ M 北京理工大学学报， ］ ． 28 北京: 清华大学出版社， 2008 ． DVB-S2 4 ) : : 2008 347-351． 131-134． ( ］ ) ［ S ． ( ， ， In-