2018年山东济南小升初数学真题及答案.doc-资料库

第1页 / 共12页

第2页 / 共12页

第3页 / 共12页

第4页 / 共12页

第5页 / 共12页

第6页 / 共12页

第7页 / 共12页

第8页 / 共12页

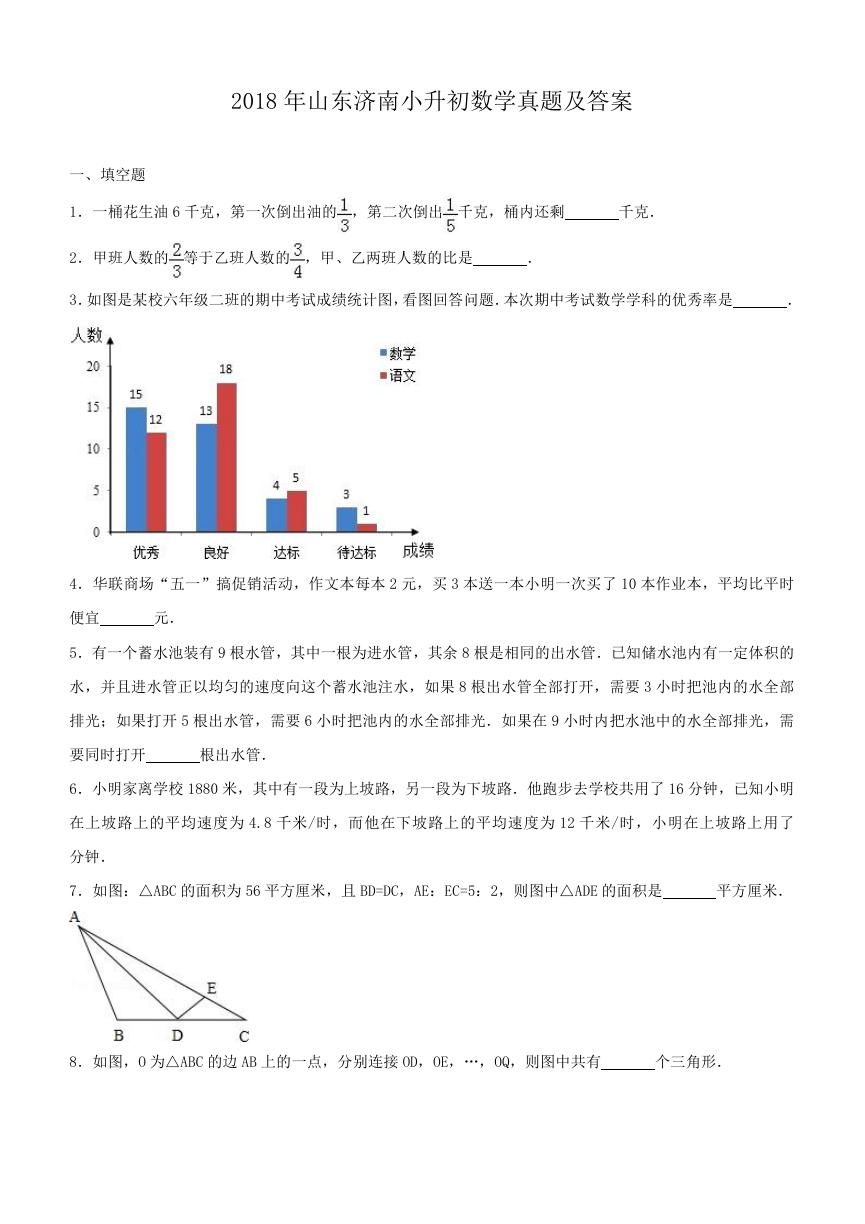
2018 年山东济南小升初数学真题及答案一、填空题 1．一桶花生油 6 千克，第一次倒出油的，第二次倒出千克，桶内还剩千克． 2．甲班人数的等于乙班人数的，甲、乙两班人数的比是． 3．如图是某校六年级二班的期中考试成绩统计图，看图回答问题．本次期中考试数学学科的优秀率是． 4．华联商场“五一”搞促销活动，作文本每本 2 元，买 3 本送一本小明一次买了 10 本作业本，平均比平时便宜元． 5．有一个蓄水池装有 9 根水管，其中一根为进水管，其余 8 根是相同的出水管．已知储水池内有一定体积的水，并且进水管正以均匀的速度向这个蓄水池注水，如果 8 根出水管全部打开，需要 3 小时把池内的水全部排光；如果打开 5 根出水管，需要 6 小时把池内的水全部排光．如果在 9 小时内把水池中的水全部排光，需要同时打开根出水管． 6．小明家离学校 1880 米，其中有一段为上坡路，另一段为下坡路．他跑步去学校共用了 16 分钟，已知小明在上坡路上的平均速度为 4.8 千米/时，而他在下坡路上的平均速度为 12 千米/时，小明在上坡路上用了分钟． 7．如图：△ABC 的面积为 56 平方厘米，且 BD=DC，AE：EC=5：2，则图中△ADE 的面积是平方厘米． 8．如图，O 为△ABC 的边 AB 上的一点，分别连接 OD，OE，…，OQ，则图中共有个三角形．

二、选择题 9．在△ABC 中，如果∠A=∠B= ∠C，则△ABC 一定是（） A．锐角三角形 B．钝角三角形 C．直角三角形 D．任意三角形 10．一个批发兼零售的文具店规定：凡一次购买铅笔 300 枝以上（不包括 300 枝），可以按批发价付款；购买 300 枝以下（包含 300 枝）只能按零售价付款．小明来该商店买铅笔，如果给学校六年级同学每人买 1 枝，那么只能按零售价付款，需要 120 元；如果多买 60 枝，那么可以按批发价付款，同样需要 120 元．若按批发价购买 6 枝与按零售价买 5 枝的款相同，那么这个学校六年级的学生有（）人． A．240 人 B．260 人 C．280 人 D．300 人三、计算 11．计算： +[1﹣（ + ）]× ．四、解答题 12．如图，梯形 ABCD 的上底 AD=10 厘米，下底 BC=16 厘米．△DFC 的高 DE=8 厘米，并把△DFC 分为面积相等的甲乙两部分，求阴影部分的面积． 13．端午节吃粽子是中华民族的传统风俗，一超市为了吸引消费者，增加消费量，特此设计了一个游戏，其规则是：分别转动如图所示的两个可以自由转动的转盘各一次，每次指针落在每一字母区域的机会均等（若指针恰好指在分界线上则重转），当两个转盘的指针所致字母都相同时，消费者就可以获得一次八折优惠买粽子的机会．（1）请表示出游戏可能出现的所有结果；

（2）若一名消费者只参加一次游戏，则他能获得八折优惠价购买粽子的可能性是多少？ 14．某商场进货员预测一种衬衫能畅销市场，就用 8 万元购进这种衬衫，面市后果然供不应求，商厦又用了 17.6 万购进了第二批这种衬衫，所购数量是第一次进量的 2 倍，但单价贵了 4 元，商厦销售这批衬衫时每件定价都是 58 元．在这两笔生意中，商厦共盈利多少元？ 15．在一条直线上依次有 A、B、C 三个港口，甲、乙两船同时分别从 A、B 港口出发，沿直线匀速驶向 C 港，最终到达 C 港．A、B 两港口的距离为 30km，B 和 C 两港口的距离是 90km，甲船的速度为 60km/h，乙船的速度为 30km/h．若两船的距离不超过 10km 时能够互相望见，问在未到达 C 港之前，甲、乙两船可以在什么时间段内互相望见？

参考答案与解析一、填空题 1．一桶花生油 6 千克，第一次倒出油的，第二次倒出千克，桶内还剩 3.8 千克．【分析】共有 6 千克，第一次倒出油的，则第一次倒出了 6× 千克，第二次倒出千克，则用总千克数减去两次倒出的即是还剩下的，列式为：6﹣6× ﹣ ．【解答】解：6﹣6× ﹣ =6﹣2﹣0.2， =3.8（千克）；答：桶内还剩下 3.8 千克．故答案为：3.8． 2．甲班人数的等于乙班人数的，甲、乙两班人数的比是 9：8 ．【分析】根据“甲班人数的等于乙班人数的，”知道甲班人数× =乙班人数× ，再逆用比例的基本性质，得出甲班人数与乙班人数的比．【解答】解：因为甲班人数× =乙班人数× ，所以甲班人数：乙班人数= ：， =（ ×12）：（ ×12）， =9：8，答：甲、乙两班人数的比是 9：8；故答案为：9：8． 3．如图是某校六年级二班的期中考试成绩统计图，看图回答问题．本次期中考试数学学科的优秀率是 42.9% ．

【分析】深色表示数学的考试成绩；先找出数学考试成绩的优秀人数，再求出总人数，然后用优秀的人数除以总人数乘 100%即可．【解答】解：15÷（15+13+4+3）×100%， =15÷35×100%， ≈42.9%；答：本次期中考试数学学科的优秀率是 42.9%．故答案为：42.9． 4．华联商场“五一”搞促销活动，作文本每本 2 元，买 3 本送一本小明一次买了 10 本作业本，平均比平时便宜 0.4 元．【分析】根据题意，买 3 本送一本，一组是 4 本，10 本里面有几个 4 本就能享受送几本，10÷4=2（组）余 2 本，也就是享受送 2 本．因此 10 本只花 8 本的钱，用每本的原价减现在的价格问题即可得到解决．【解答】解：买 3 本送一本，一组是 4 本，10 本里面有几个 4 本就能享受送几本， 10÷4=2（组）…2（本），也就是享受送 2 本．因此 10 本只花 8 本的钱， 2﹣2×8÷10， =2﹣16÷10， =2﹣1.6， =0.4（元）；答：平均每本比平时便宜 0.4 元．故答案为：0.4． 5．有一个蓄水池装有 9 根水管，其中一根为进水管，其余 8 根是相同的出水管．已知储水池内有一定体积的

水，并且进水管正以均匀的速度向这个蓄水池注水，如果 8 根出水管全部打开，需要 3 小时把池内的水全部排光；如果打开 5 根出水管，需要 6 小时把池内的水全部排光．如果在 9 小时内把水池中的水全部排光，需要同时打开 4 根出水管．【分析】设每根出水管每小时出水 1 份，根据“如果 8 根出水管全部打开，需要 3 小时把池内的水全部排光；如果打开 5 根出水管，需要 6 小时把池内的水全部排光．”利用两次的份数差可以分别求出进水管的速度和蓄水池内原有的水的份数，列式分别为：（5×6﹣8×3）÷（6﹣3）=2 份，5×6﹣2×6=18（份）；然后再根据（蓄水池内原有的水的份数+9 小时进水管的份数）÷9，即可求出需要同时打开出水管的根数．【解答】解：设每根出水管每小时出水 1 份，进水管的速度为：（5×6﹣8×3）÷（6﹣3）， =6÷3， =2（份）；蓄水池内原有的水为： 5×6﹣2×6， =30﹣12， =18（份）； 9 小时内把水池中的水全部排光，需要打开出水管的根数是：（18+2×9）÷9， =36÷9， =4（根）；答：如果在 9 小时内把水池中的水全部排光，需要同时打开 4 根出水管．故答案为：4． 6．小明家离学校 1880 米，其中有一段为上坡路，另一段为下坡路．他跑步去学校共用了 16 分钟，已知小明在上坡路上的平均速度为 4.8 千米/时，而他在下坡路上的平均速度为 12 千米/时，小明在上坡路上用了 11 分钟．【分析】根据题意可得到本题的等量关系：上坡的时间+下坡的时间=16，上坡的路程+下坡的路程=1880，依题意列出方程求解．【解答】解：4.8 千米/小时=4.8×1000÷60=80 米/分， 12 千米/小时=12×1000÷60=200 米/分．设上坡的时间是 x 分钟，下坡的时间是 16﹣x 分钟． 80x+200×（16﹣x）=1880，

80x+3200﹣200x=1880， 3200﹣120x+120x=1880+120x， 1880+120x﹣1880=3200﹣1880， 120x÷120=1320÷120， x=11，答：小明在上坡路上用了 11 分钟．故答案为：11． 7．如图：△ABC 的面积为 56 平方厘米，且 BD=DC，AE：EC=5：2，则图中△ADE 的面积是 20 平方厘米．【分析】因为 BD=DC，根据高一定时，三角形的面积与底成正比例的性质可得三角形 ADC 的面积= 三角形 ABC 的面积=28 平方厘米；AE：EC=5：2，则 AE：AC=5：7，同理可得三角形 ADE 的面积= 三角形 ADC 的面积= × 28=20 平方厘米，由此即可解答．【解答】解：因为 BD=DC，三角形 ABC 的面积是 56 平方厘米，所以三角形 ADC 的面积= 三角形 ABC 的面积= ×56=28（平方厘米）； AE：EC=5：2，则 AE：AC=5：7，所以三角形 ADE 的面积= 三角形 ADC 的面积= ×28=20（平方厘米），答：三角形 ADE 的面积是 20 平方厘米．故答案为：20． 8．如图，O 为△ABC 的边 AB 上的一点，分别连接 OD，OE，…，OQ，则图中共有 37 个三角形．【分析】根据图形的计数原原理和方法，按照一定顺序观察思考，首先把整个图形分成左右两部分，利用数

角的方法，左边三角形的个数是：1+2+3+4+5+6=21，同样右边三角形的个数是 1+2+3+4+5=15；左右两部分合起来是一个大三角形，由此即可解答．【解答】解：根据题干分析可得：21+15+1=37（个），答：一共有 37 个三角形．故答案为：37．二、选择题 9．在△ABC 中，如果∠A=∠B= ∠C，则△ABC 一定是（） A．锐角三角形 B．钝角三角形 C．直角三角形 D．任意三角形【分析】因为∠A=∠B= ∠C，所以三角形三个内角的度数比是 1：1：3，即三角形中最大的角占三角形内角和的，因为三角形的内角和是 180 度，进而根据按比例分配知识求出最大角，然后判定出三角形的类型．【解答】解：因为∠A=∠B= ∠C，所以三角形三个内角的度数比是 1：1：3， 1+1+3=5（份），最大角：180°× =108°；所以该三角形是钝角三角形；故选：B． 10．一个批发兼零售的文具店规定：凡一次购买铅笔 300 枝以上（不包括 300 枝），可以按批发价付款；购买 300 枝以下（包含 300 枝）只能按零售价付款．小明来该商店买铅笔，如果给学校六年级同学每人买 1 枝，那么只能按零售价付款，需要 120 元；如果多买 60 枝，那么可以按批发价付款，同样需要 120 元．若按批发价购买 6 枝与按零售价买 5 枝的款相同，那么这个学校六年级的学生有（）人． A．240 人 B．260 人 C．280 人 D．300 人【分析】本题有两个等量关系：一是批发价购买 6 枝与按零售价购买 5 枝的款相同；二是用 120 元按批发价付款比按零售价付款可以多购买 60 枝．可据此来列方程解答．【解答】解：设这个学校六年级的学生有 x 人， ×5= ×6， = ，

资料库

2018年山东济南小升初数学真题及答案.doc

相关推荐

小升初

热门标签

最新资料