第1页 / 共40页
第2页 / 共40页
第3页 / 共40页
第4页 / 共40页
第5页 / 共40页
第6页 / 共40页
第7页 / 共40页
第8页 / 共40页
数学模型程序代码-Matlab-姜启源-第一章-建立数学模型.pdf
第 1 章 建立数学模型
教材中给出原始数据， 结合模型， 得到结果。 但如何求得结果这一过程没有
给出，实际上要用 MATLAB 软件编写程序来求得，这应该交给实验课来完成。
考虑到上学期同学们刚学习 MATLAB 语言，编程能力不强，所以有关的程序给
出来供同学们进行验证。要求同学们要读懂程序。
1.（求解，编程）如何施救药物中毒 p10~11
人体胃肠道和血液系统中的药量随时间变化的规律（模型） ：
d
x
d
t
d
y
d
t
,
x
x
(0)
1100
x
,
y
y
(0)
0
(
,
0)
其中，x(t)为 t 时刻胃肠道中的药量， y(t)为 t 时刻血液系统中的药量， t=0 为
服药时刻。
1.1（求解）模型求解 p10~11
要求：
① 用 MATLAB 求解微分方程函数 dsolve求解该微分方程（符号运算） 。
② 用 MATLAB 的化简函数 simplify 化简所得结果。
③ 结果与教材 P11上的内容比较。
提示： dsolve和 simplify 的用法可用 help 查询。建议在命令窗口中操作。
★ 求解的语句及运行结果：
>> [x,y]= dsolve( 'Dx=-a*x' ,'Dy=a*x-b*y'
>> disp([x,y])
[ 1100*exp(-a*t), exp(-a*t)*exp(-b*t)*((1100*a*exp(a*t))/(a - b) - (1100*a*exp(b*t))/(a - b))]
,'x(0)=1100' ,'y(0)=0' );
1
>> disp(simplify([x,y]));
[ 1100*exp(-a*t), (1100*a*exp(-t*(a + b))*(exp(a*t) - exp(b*t)))/(a - b)]
1.2（编程）结果分析 p11
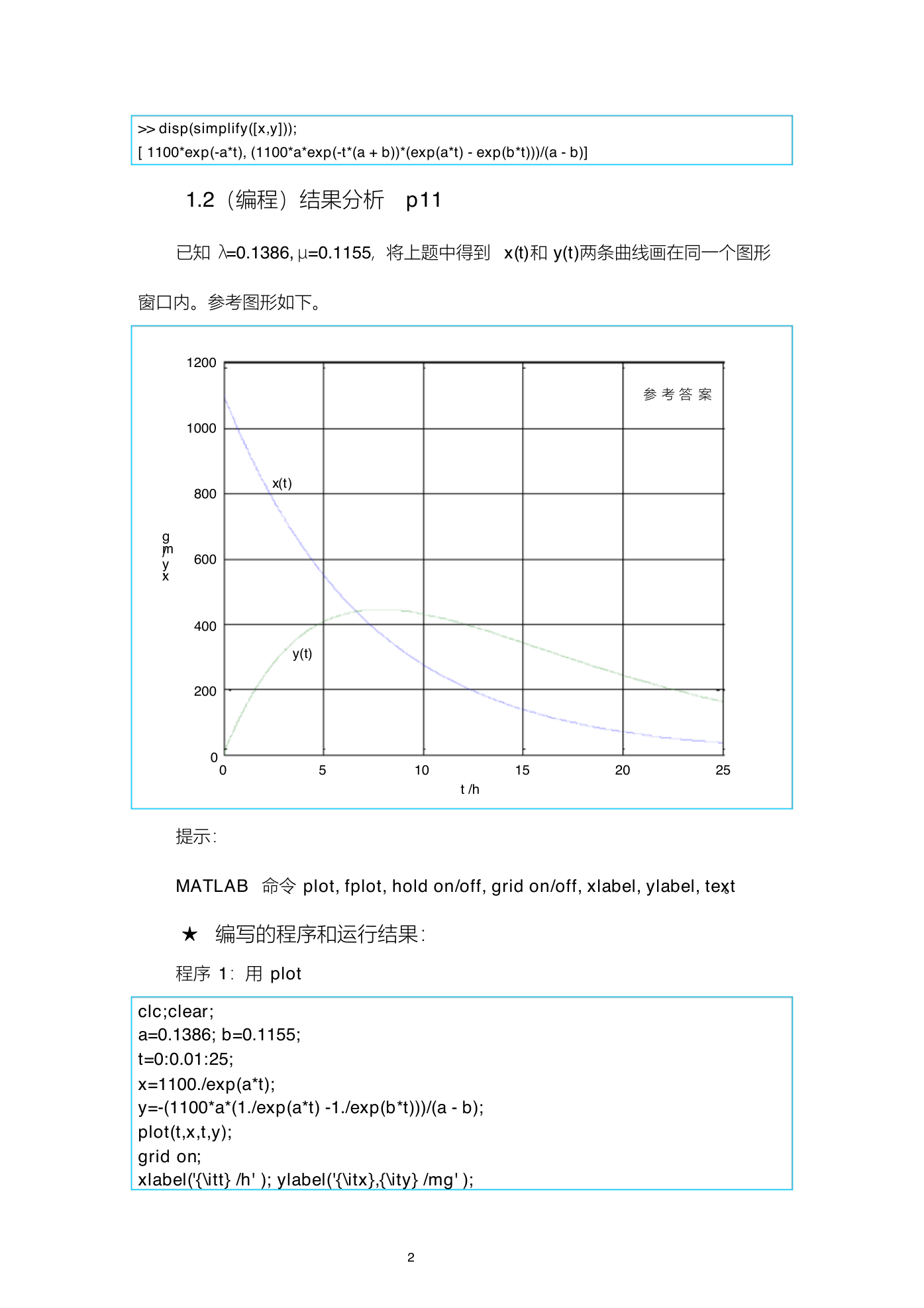
已知 λ=0.1386, μ=0.1155，将上题中得到 x(t)和 y(t)两条曲线画在同一个图形
窗口内。参考图形如下。
x(t)
y(t)
1200
1000
800
600
400
200
g
/m
x,y
0
0
提示：
参 考 答 案
5
10
15
20
25
t /h
MATLAB 命令 plot, fplot, hold on/off, grid on/off, xlabel, ylabel, text。
★ 编写的程序和运行结果：
程序 1：用 plot
clc;clear;
a=0.1386; b=0.1155;
t=0:0.01:25;
x=1100./exp(a*t);
y=-(1100*a*(1./exp(a*t) -1./exp(b*t)))/(a - b);
plot(t,x,t,y);
grid on;
xlabel('{\itt} /h' ); ylabel('{\itx},{\ity} /mg' );
2
text(2,1100/exp(a*2),'
text(3,-(1100*a*(1/exp(a*3) - 1/exp(b*3)))/(a - b), '
{\itx}({\itt})' );
{\ity}({\itt})' );
程序 2：用 fplot 和匿名函数
clc;clear;
a=0.1386; b=0.1155;
fplot(@(t)[1100/exp(a*t),-(1100*a*(1/exp(a*t) - 1/exp(b*t)))/(a - b)],[0 25]);
grid on;
xlabel('{\itt} /h' ); ylabel('{\itx},{\ity} /mg' );
text(2,1100/exp(a*2),'
text(3,-(1100*a*(1/exp(a*3) - 1/exp(b*3)))/(a - b), '
{\ity}({\itt})' );
{\itx}({\itt})' );
2.（编程，验证）商人们怎样安全过河 p8~9
三名商人各带一个随从乘船渡河， 一只小船只能容纳二人， 由他们自己划行。
随从们密约，在河的任一岸，一旦随从的人数比商人多，就杀人越货。但是如何
乘船的大权掌握在商人们手中。商人们怎样才能安全渡河呢？
[模型构成 ]
决策： 每一步（此岸到彼岸或彼岸到此岸）船上的人员。
要求：在安全的前提下（两岸的随从数不比商人多） ，经有限步使全体人员
过河。
xk 第 k 次渡河前此岸的商人数
yk 第 k 次渡河前此岸的随从数
xk , yk=0,1,2,3; k=1,2,
过程的状态
sk=(xk , yk)
允许状态集合 S={(x, y) x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2}
uk 第 k 次渡船上的商人数
vk 第 k 次渡船上的随从数
uk , vk=0,1,2; k=1,2,
3
决策 dk=(uk , vk)
允许决策集合 D={(u , v) u+v =1, 2}
状态转移律
sk+1=sk+(-1)kdk
[多步决策问题 ]
求 dk D(k=1, 2,
, n), 使 sk S, 并按转移律由 s1=(3,3) 到达 sn+1=(0,0)。
2.1（编程）求允许决策集合 D 和允许状态集合 S
D 是 2 行多列矩阵，每一列是一个决策。
S 是 2 行多列矩阵，每一列是一种状态。
要求：
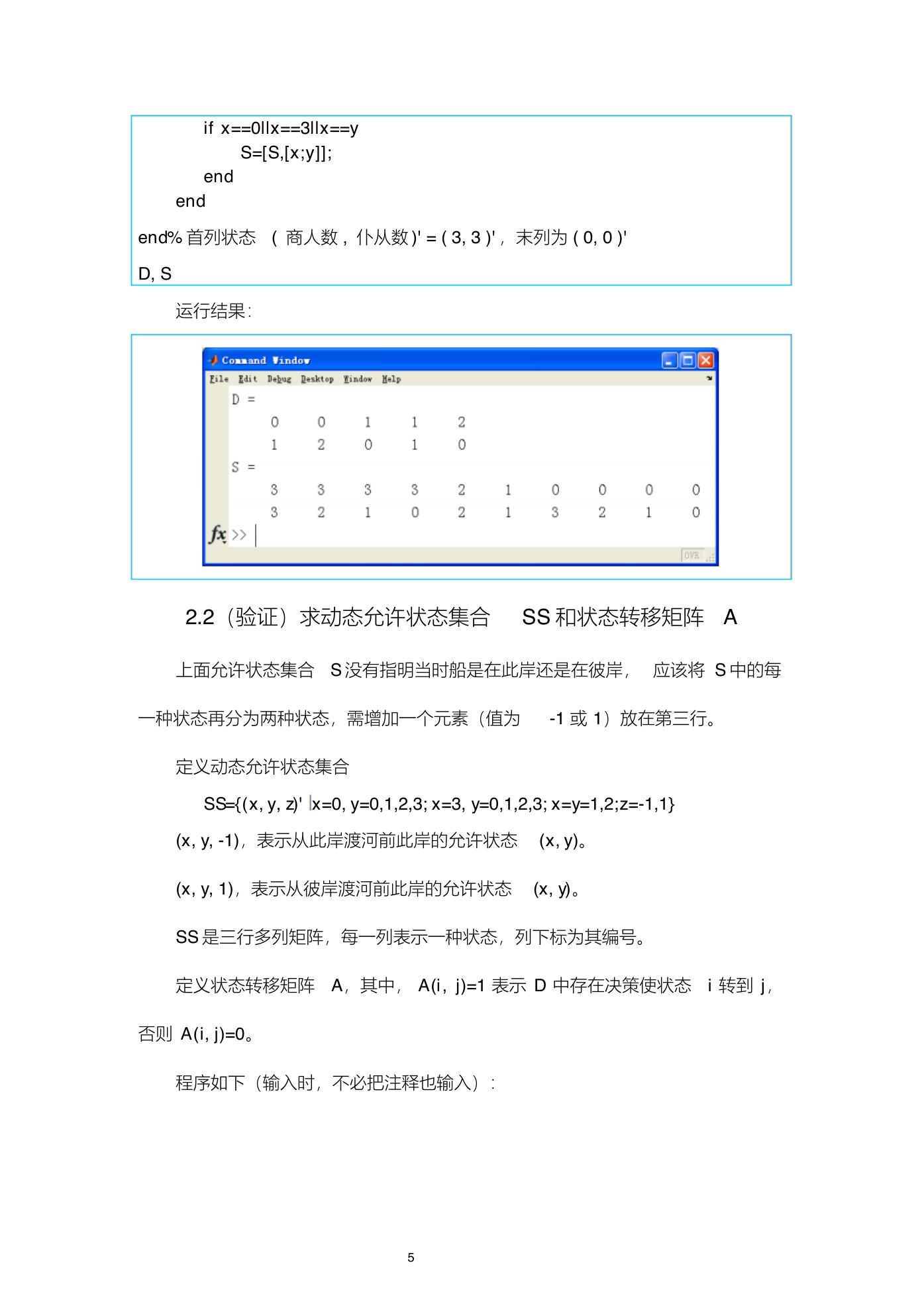
① 编写程序求 D 和 S，并输出。
② S 的第一列是 [3,3]'，最后一列是 [0,0] '。
★ 编写的程序和运行结果：
程序：
clear; clc;
% 求允许决策集合 D（2×n1，n1 种决策）
D=[];
for u=0:2
for v=0:2
if u+v==1||u+v==2
D=[D,[u;v]];
end
end
end
% 求允许状态集合 S（2×n2，n2 种状态）
S=[];
for x=3:-1:0
for y=3:-1:0
4
if x==0||x==3||x==y
S=[S,[x;y]];
end
end
end% 首列状态 ( 商人数 , 仆从数 )' = ( 3, 3 )' ，末列为 ( 0, 0 )'
D, S
运行结果：
2.2（验证）求动态允许状态集合 SS 和状态转移矩阵 A
上面允许状态集合 S 没有指明当时船是在此岸还是在彼岸， 应该将 S 中的每
一种状态再分为两种状态，需增加一个元素（值为 -1 或 1）放在第三行。
定义动态允许状态集合
SS={(x, y, z)' x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2;z=-1,1}
(x, y, -1)，表示从此岸渡河前此岸的允许状态 (x, y)。
(x, y, 1)，表示从彼岸渡河前此岸的允许状态 (x, y)。
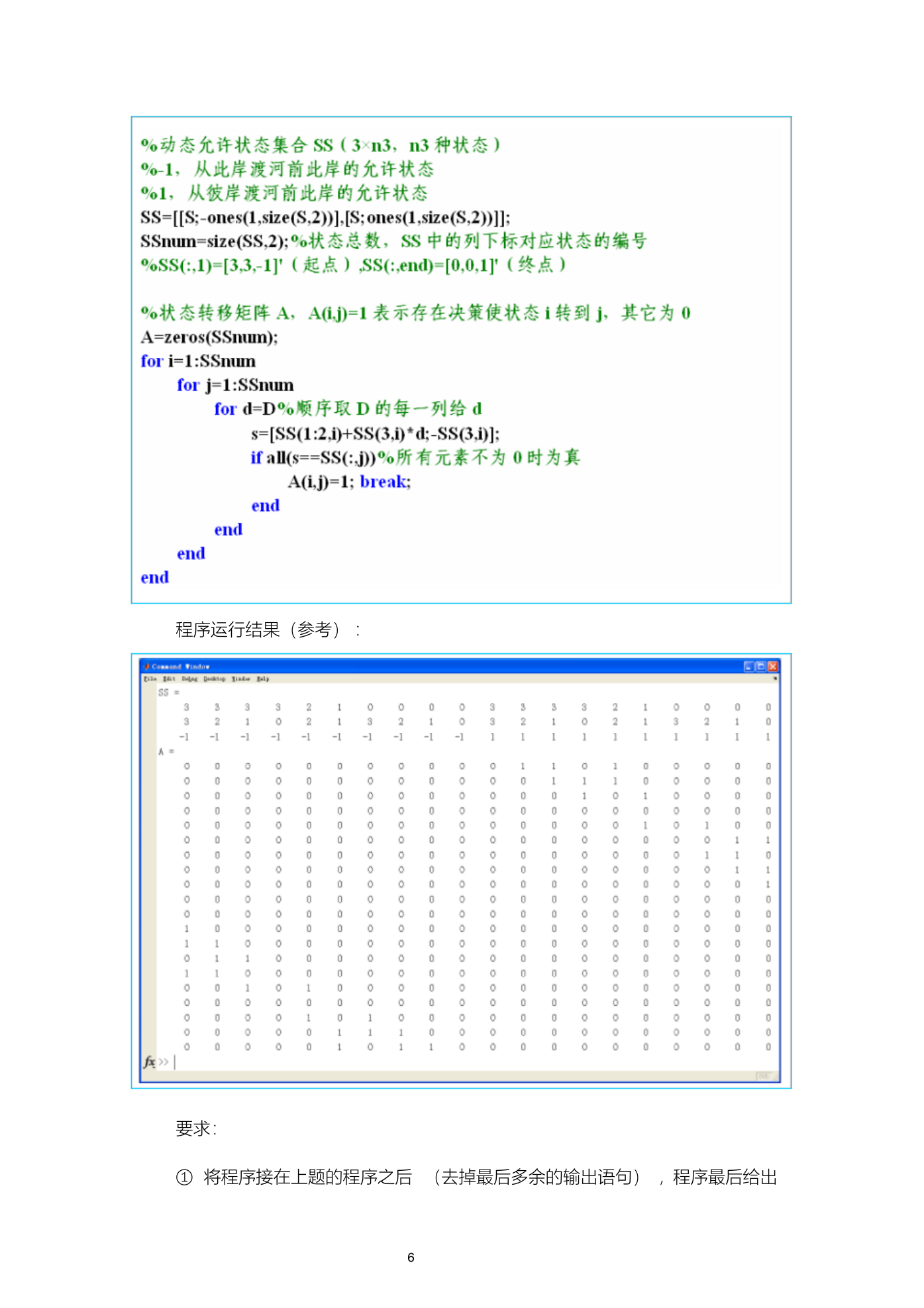
SS 是三行多列矩阵，每一列表示一种状态，列下标为其编号。
定义状态转移矩阵 A，其中， A(i, j)=1 表示 D 中存在决策使状态 i 转到 j，
否则 A(i, j)=0。
程序如下（输入时，不必把注释也输入）：
5
程序运行结果（参考） ：
要求：
① 将程序接在上题的程序之后 （去掉最后多余的输出语句） ，程序最后给出
6
显示 SS和 A 的语句。
② 运行程序，输出 SS 和 A。对照参考答案，如数值不一致，请检查程序。
MATLAB 函数 all 的用法见提示。
★ 运行的完整程序和运行结果：
程序：
clear; clc;
% 求允许决策集合 D（2×n1，n1 种决策）
D=[];
for u=0:2
for v=0:2
if u+v==1||u+v==2
D=[D,[u;v]];
end
end
end
% 求允许状态集合 S（2×n2，n2 种状态）
S=[];
for x=3:-1:0
for y=3:-1:0
if x==0||x==3||x==y
S=[S,[x;y]];
end
end
end% 首列状态 ( 商人数 , 仆从数 )' = ( 3, 3 )' ，末列为 ( 0, 0 )'
% 动态允许状态集合 SS（3×n3，n3 种状态）
%-1 ，从此岸渡河前此岸的允许状态
%1 ，从彼岸渡河前此岸的允许状态
SS=[[S;-ones(1,size(S,2))],[S;ones(1,size(S,2))]];
SSnum=size(SS,2);% 状态总数， SS中的列下标对应状态的编号
%SS(:,1)=[3,3,-1]' （起点）， SS(:,end)=[0,0,1]'（终点）
7
% 状态转移矩阵 A，A(i,j)=1 表示存在决策使状态 i 转到 j，其它为 0
A=zeros(SSnum);
for i=1:SSnum
for j=1:SSnum
for d=D% 顺序取 D 的每一列给 d
s=[SS(1:2,i)+SS(3,i)*d;-SS(3,i)];
if all(s==SS(:,j))% 所有元素不为 0 时为真
A(i,j)=1; break;
end
end
end
end
SS, A
运行结果：
2.3（验证）给出一个商人们安全过河的方案
程序如下（输入时，不必把注释也输入） ：
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
