基于STAR模型的汇率预测.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书资料大小：0.79M 资料格式：pdf 举报版权申诉

xiaocuiman-7191693-4744302543417841095.pdf-第1页.png

第1页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第2页.png

第2页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第3页.png

第3页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第4页.png

第4页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第5页.png

第5页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第6页.png

第6页 / 共7页

xiaocuiman-7191693-4744302543417841095.pdf-第7页.png

第7页 / 共7页

文本预览

经济与金融基于 STAR 模型的中国货币需求函数研究张蕾（武汉体育学院经济管理学院，武汉 430079）摘要：本文对我国货币需求的短期误差修正模型进行非线性检验并发现指数平滑转换自回归模型更加符合我国短期的货币需求函数。通过检验，我们发现非线性模型的转换变量为滞后一期的真实国民收入，该结论与我国经济发展状况相吻合。另外，通过检验发现非线性模型具有较强的预测能力。因此，非线性模型将会给货币政策的正确制定和有效实施提供更具参考价值的作用。关键词：货币需求；ESTAR；非嵌套检验引言货币需求影响着一国货币政策的正确制定和有效实施货币需求函数的稳定性并对其进行研究别来考察货币需求函数的长期稳定性和对短期货币需求的调控力设：货币需求方程是线性的。。。但是目前主要采用的是协整和建立误差修正模型（。正是由于其重要性，目前许多学者十分关注各国）的方法分这种研究都不可避免的隐含一个前提假 VECM 。。预防动机和投机动机、目前学术界主要用收入。利率、稍加推敲，就会发现线性模型的局限性。线性模型假定分析对象可表示为一些影响因素的线性函数根据凯恩斯的货币需求理论，影响货币需求的主要有三种动机，即交易动机通货膨胀率等变量来反、映这三个动机根据线性模型的含义，货币需求函数的线性模型即用以上几个变量的线性形式来反映货币需求量因为不同的经济时期，国家的经济政策和发展水平会不同，居民。对未来经济的不同预期，再加上居民生活环境的改变可能会导致这些变量对货币需求量产生不同影响，甚至消失或再次影响如社会保障体制是否完善会使居民的货币需求收入弹性值发生改变；又如，整个经济形势的。高涨和低迷也会使货币需求利率弹性值发生变化就中国而言，最典型的例子就是房价，随着我国住宅商品化，房地产已经成为我国的支柱产业之一，和以前的学者不同，现在越来越多的学者将房地产市场的发展也作为影响货币需求量的因素之一相信随着经济环境和市场的不断变化，对货币需求量影响的因素会不断的变化年的数据对 Zaghini[2]研美国在此期间的线性货币方程作出修正，指出其应该是以利率为转换变量的非线性形式究了欧洲地区狭义货币（鲁克波 M1 。尔等[3]通过建立模型考察了德国货币需求函数的稳定性，同时关注可能存在的非线性关系，尤其关注德国统一对货币（另外，国外已经有学者对中国的货年的数据，将通货膨胀率作为转换变量，对中国的货币需求进行了非线性研究，如币需求建立了平滑转换自回归的非线性模型，该研究结论是：当通胀率超过时，物价水平就开始影响到实但是，国内很少有学者会分析货币需求函数的非线性特征，货币体经济人的经济决策，此时应对其进行调控）需求方程，指出其呈现出明显的非线性效应，并给出了相应的转换方程在国外已经有学者对货币需求函数的非线性问题做出了研究，如：）需求的影响，只有微弱的证据证明存在非线性特征 1867-1977 1987-2004 等[1]利用等[4]利用和。Calza LSTAR M1 Darran Sarno 。 5% 。。。。收稿日期：2010-04-21 作者简介：张蕾，武汉体育学院经济管理学院讲师博士，。 MANAGEMENT REVIEW Vol.24 No.10 2012 11 （）

经济与金融政策的制定和实施也主要依据线性模型，因此，常会出现在不同的时间段研究结论不一致的情况，从而给出的货币政策建议也不同[5]。鉴于线性方程的局限性和国内外学者对不同国家线性货币需求方程的实证结果，本文对我国货币需求函年代以来，我国金融体制改革迅速发展，国家对物价稳定性问题越来越数的线性特征提出质疑，特别是从重视，国债在金融体制改革和经济环境迅猛变化的大背景下，我国的货币需求函数是线性还是非线性的？这个问题对货币政策的正确制定有着很重要的参考价值如果是非线性的，转换变量是什么？目前，我国能够通过宏观调控很好的处理物价过度波动的问题，那么，这个转换变量仍然是上文国外学者所提出来的通货膨胀率吗？政策性金融债券和央行票据逐步纳入公开市场业务交易工具的范围[6]。、中央银行融资券、 90 。本文将采用平滑转化自回归模型对以上的疑问给出检验本。文首先对这种检验方法做出简单的介绍，然后将这种检验方法的结果与中国经济发展历程相对照，看是否与实际相吻合这也是目前使用最多，相对严谨的检验方法。最后给出结论。。 STAR 模型及其在货币需求方程中的运用 x1t （ zt = 其中，， x2t 变量的滞后量数，，（ st G γ 在） TAR 。 LSTAR 在 ESTAR 1、平滑转换自回归（STAR）模型概述目前，非线性时间序列有三种机制转换模型（ switching regime models （）和门限自回归模型（ Markov Switching Regime model 假定，某一特定的时点，时间序列的运动方式是从一种机制（的[7 ， 8]。， MSR 但在实际生活中，有些机制的转换（）却并不是离散跳跃的，而是一个连续的等[9]在他们的研究中比较早地提出根据实际情况模拟机制逐渐转换过程的想法，而后 switching Threshold Autoregression model 。）其中，马尔可夫机制转换模型）都暗含了一个）跳跃到了另一种机制，同时这种跳跃是离散逐渐变化的过程、。 Terasvirta[10]又发展， TAR Bacon 了一种新的能够体现机制的连续性变换的模型， c 为需要考察的自变量，），， ′ xkt 准′ … ，，）为转换函数，反映了机制的转换过程，并且该转换函数是在（ st γ c 模型如下：平滑转换自回归模型（ STAR （），）（ σ2 1 0 自变量可以是外生变量，也可以是因上取值的连续函， u~iid 为自变量的系数 ——— ，） st 和 yt =准′zt+θ′ztG 典型的， … （ γ STAR ， T 。G t=1 +ut ）到。。 θ′ 1 u regime ，）的函数形式最常用的就是对数函数（ c Logistic STAR ， LSTAR Exponential STAR ， ES－ 0 ）和指数函数（中，转换函数的形式为：，（ st G γ 中，转换函数的形式为：）， c = 1 （ 1+exp{-γ ） } st -c γ>0 （） 2 st （ st=t 。γ st -c ，） c =1-exp{-γ ，（ st G γ st 变量制之间的转折点另一个机制转变的平滑度是突然的中有不同的运动轨迹）2} γ>0 是转换变量，它可以是一个滞后的内生变量也可以是一个外生变量也可以是一个线性时间趋势（和），这样该模型就会有一个平滑的参数变化（） 3 的研究表明，转换是门限值，表示两个机是转换函数的斜率，度量了从一个机制向另一个机制转换的速度并决定了从一个机制向时，不同机制之间的转换处对称，但在转换过程模型估计之前，就有必要就模型是否为非线性进行检验，和 STAR ）用合适的泰勒序列近似值替代，并且这种方法可用来决定时间序列，，（ st c G γ 模型为了避免阶数较低而可能会出现问题，我们选择了三阶泰勒展开式 STAR 模型表明两个机制具有类似的动态性在进行提出可以将转换函数转换函数为对数函数的。模型称为转换函数是。 γ→∞ 型的，大约在当 LSTAR。 Luukkonen Teasvirta Terasvirta 是适合于得到近似转换函数，并估计以下的辅助回归模型：模型还是。ESTAR ESTAR LSTAR 。Lin 。c 。。 U c 对辅助回归模型的线性检验为 H0 ∶ β1=β2=β3=0。值作为设定转换变量的标准[11]。 yt =β0′zt +β1′zt st+β2′zt s2 t +β3′zt s3 零假设可以采用 t +et 检验。 LM 在模型拒绝线性假设之后，对于采用假设时，选择最小的模型，可以采用下述检验： p （） 4 当不止一个解释变量拒绝线性还是 LSTAR ESTAR （） 5 H01 ∶ β3=0 12 （管理评论 Vol.24 No.10 2012 ）

如果拒绝，但是拒绝 H01 假设，则选择，则选择 LSTAR 模型①。 LSTAR H03 H02 H03 ∶ β1=0| β2=β3=0 模型；如果接受但是拒绝 H01 H02 ∶ β2=0| β3=0 经济与金融，则选择 H02 ESTAR 模型；如果接受（） 6 （） 7 和 H01 2、STAR 模型在货币需求方程中的应用一直以来，学术界对货币需求投机动机的表示变量存在争议，即究竟应该采用利率还是预期通货膨胀率检验的方法，该方法主要是用于判断哪种变本文将会采用该方法及其他非嵌套检验来考察这两个因素对我国货币来反映持有货币的机会成本[12]？量对分析对象产生更有效的作用[2 ，， 5 7]。需求量的影响大小，然后对机会成本变量做出选择 Mackinnon Davidson 提出了和 J 变量选好之后，我们将在货币需求量和影响因素之间建立长期均衡方程：。货币数量， Zt 在对长期均衡方程作出协整检验之后，本文根据萨根提出的误差修正模型建立短期货币需求方程：准假设代表货币需求的影响因素（的滞后期变量）， α′ 机会成本变量和 GDP、 Mt 。 Mt=α′Zt+ut。其中， Mt 为待估参数， ut 代表时刻的符合白噪声标 t ΔMt =β′ΔZt +λECt-1+ut ， … ， T ， u~iid （ 0 ， σ2 u ） t=1 ）中式（ 8 ECt-1 为误差修正项，反映了短期货币需求偏离长期均衡的程度[13]， λ 衡方程对发生偏离的短期货币的调节速度符合白噪声假设。ut 。（） 8 为调节参数，反映了长期均我们知道，长期货币需求函数反映的是一种趋势，而短期货币需求函数更能反映在某一样本区间或者说换句话说，短期货币需求方程更能较为准确的刻画当下或一定本文将对式（） 8 模型，并依据上文的判断方法，在较短的时间内影响因素对货币需求的影响时间段货币需求量的变化过程，因此，对短期货币需求方程的非线性检验将更具有实际意义进行非线性特征的检验，如果结论是支持非线性假设的，将建立相应的给出模型的具体形式 STAR 。。 STAR 。 STAR 模型在中国货币需求方程中的实证检验 1、货币需求方程的建立（）数据的选取和处理 1 本文的主要目的在于考察我国短期货币需求函数是否具有非线性特征，与货币量的统计标准无关，因此对于交易需求变量，我们用真实国内生产总值（）来代表，。 y 待非嵌套检验之后，对机会作为考察变量并剔除价格因素）共同来反映 M0 R1 。 1992 季度的数据作为样本，为了避免季节因素的影响，我们对每个变量通过移动平均的本文均使用季度数据②。。根据数据的可获得性本文选取我们随机挑选了而机会需求变量暂时用通货膨胀率（）和一年期名义存款利率（ π 需求变量作出选择，然后建立长期货币需求方程年第方法做出了季节调整并将各个变量取对数[15]。（ yt =log 数据处理结果： GDPt /cpit 季度到 M0 t /cpit 年第），）， 2009 R1t =log 1 4 （），（ R1t πt =log cpit /cpit-1 ）是名义货币总量，是消费物价指数，反映了物价水平，下标和表示相的数据均来自中国经济金融数据库，通货膨胀率由季度数据环比求得 π 。 cpi t t-1 cpi （代表真实货币余额， M0 和 m0 t =log 名义其中应的时点 m0 。M0、R1、 GDP （）机会成本变量的选取 2 哈维（ Harvey 拟合优度 R2 值或校正者施瓦茨信息准则（ SIC 。第一种方法是比较）或）将非嵌套检验的方法分为两类，其前提是几个模型需具相同的因变量 R2 值，选取其较高的模型，当），选择其值较低的模型。 R2 值不具备可比性时，也可以比较赤池信息准则（ AIC 第二种方法是目前常用的戴维森麦金农检验（ J ），该检验方法是将某一方程的因变量作为自变量带入另一方程，然后比较其 - Mackinnon Jtest 统计量的值不显著可能意味着该因变量所代表的模型不为真具有两种机会成本变量的货币需求函数进行检验，选择最合适的模型，避免机会成本变量的盲目性[16]。。 Davidson- 统计量的值， t 本文出于严谨性考虑，分别用两种方法对以下 t 和， Terasvirta Franses[13]指出上述检验只能应用于特定的 ①Dijk 间进行选择仍然是一个需要进一步深入研究的课题 ②叶光利用中期都发生了结构变化，因而不建议使用年度数据估计货币需求函数统计量对改革开放 SupF、MeanF STAR 和 30 Lc 模型，而不能简单地一般化如何在这两个。 STAR 模型（ LSTAR 和）之 ESTAR 。年来中国货币需求函数的稳定性进行检验，结果表明，和 M2 的货币需求函数在年代 90 M1 。 MANAGEMENT REVIEW Vol.24 No.10 2012 13 （）

经济与金融 Model 1 ： m0t=f1 ： m0t=f2 Model 2 的估计量，） R1t ，） πt （ yt （ yt 做自变量带入 m 0 t 从表的 J 1 检验结果显示，将，显著性很高，说明 0.78 0.44 ， p Model 1 Model 2 值为兼容不显著，进一步证明另外， 0.0000 计量为为真，于 0.992＞0.977 优于低（文认为将一年期名义存款利率（来构建货币需求方程是合理的 R2 较高（ Model 1 的拟合值），故 -2.76＜-1.71 的结论 Model 2 Model 2 R1 Model 2 Model 1 可能不为真；相反，将不相对值较通过检验本 Model 2。）作为机会成本变量 Model 1 ）而 AIC 。 Model 2 Model 2 时 t 统计量为 12.26 的估计量作为解释变量带入 Model 1 表 1 Model1 和 Model2 的非嵌套检验结果值为， p 后， t 统 Model1 Model2 J 检验 12.26（0.0000） 0.78（0.44） AIC R2 -2.76 0.992 -1.71 0.977 注：括号内数字表示概率值。 p 。（）线性误差修正模型的建立 3 为了保证不出现伪回归，我们运用检验结果显示其在量在一阶差分后， PP 大特征值检验的方法对变量之间的协整关系给出检验，根据赤池准则（ 1% PP 检验方法[17]对三个变量进行单位根检验的显著性水平下均呈现出稳定的趋势结果显示，三个变紧接着，我们采用迹检验和最 yt、R1t m0 t 和。。）我们选择二期滞后[18]，结果见表 AIC 2。变量（m0 t、yt、R1t）变量（m0 t、yt、R1t） H0 r=0 r≤1 H0 r=0 r≤1 表 2 m0 t、yt 和 R1t 之间的迹检验 H1 r≥1 r≥2 tλ 50.47 13.87 表 3 m0 t、yt 和 R1t 之间最大特征根检验 H1 r≥1 r≥2 tm 36.6 12.89 临界值（5%） 29.8 15.49 临界值（5%） 21.13 14.26 结论 r=1 结论 r=1 迹检验和最大特征根检验均显示存在一个协整关系我们得到关于。误差修正模型③： m0 t =1.21+0.778yt -0.184R1t +εt （）（）（ 7.36 57.1 -11.79 ）的长期均衡方程，括号内为 m0t t 统计量：（） 9 Δm0 t=β0+β1ect-1+β2Δyt-1+β3Δyt-2+β4ΔR1t-1+β5ΔR1t-2+β6Δm0t-1+β7Δm0t-2+ut 其中，， m 0t=1.21+0.778yt -0.184R1t 。 ect=m0t- m 0t 长期方程的估计结果告诉我们真实国民收入和利率对长期货币需求的影响均很显著，且前者的影响力度但是，值得注意的是，货币需求的利率弹性呈逐渐年我国实行利率体制改革，除对商业银行零售业务利率实施管制外，央行对其他利率基本年央行连续对基准利率进行了在利率逐步市。相对后者更大，说明目前我国仍然以交易性货币需求为主增长的趋势[19]。1994 放开[20]。1994-2009 场化的背景下，我们相信利率对货币需求的影响将会进一步增强[20]，投资者对利率的敏感性也会越来越高次调整，其幅度和频率超过以往任何时期。 21 。（） 10 2、非线性检验及 STAR 模型的建立根据本文第二部分的检验过程，首先建立辅助回归模型，结合本文的研究对象，需要估计的方程为： Δm0 t =λ0′zt +λ1′zt st+λ2′zt s2 （ t +λ3′zt s3 ）为相应的待估参数， st 11 11 st。。λi 代表式（ i=0-3 检验虚拟假设：）中的解释变量），利用如果接受虚拟假设，表示模型为线性，只需用式（其中， zt 别作为转换变量带入式（换变量变量都无法拒绝虚拟假设，说明无法用非线性的量，说明该模型具有非线性特征，若不止一个解释变量拒绝取，检验结果见表 ③暂时不做估计，在模型中给出参数的最后估计结果 STAR 3。 LM STAR 。 H0 ∶ λ1=λ2=λ3=0 （ t +et 为待定的转换变量） 11 将所有的解释变量分找出拒绝线性假设的解释变量以确定转）表示短期货币需求方程即可，如果所有的解释模型来表示这个序列，反之只要存在拒绝原假设的变值最大的原则选，转换变量根据值最小或 11 。 H0 p F 14 （管理评论 Vol.24 No.10 2012 ）

转换变量 F 统计量临界值（5%）表 3 线性检验结果 ect-1 △yt-1 △yt-2 △R1t-1 R1t-2 △m0t-1 △m0t-2 1.06 2.68 1.5 0.62 0.77 2.11 2.15 1.84 1.84 1.84 1.84 1.84 1.84 1.84 经济与金融结论接受拒绝接受接受接受拒绝拒绝故线性误差修正模型不合适检验结果告诉我们，转换变量为根据在上述检验基础之上，我们将。 F 时在 Δyt-1、Δm0t-1、Δm0t-2 值最大原则我们选择的显著性水平下拒绝模型为线性的虚拟假设，作为延迟变量（） 2.68＞2.15＞2.11 。 5% Δyt-1 模型运用到短期货币需求方程中并改写式（）： 8 ））， σ2 12 ），我们将判断其具体形， … ），其余变量及参数的含义同上，（ 0 u~iid 针对式（，） st （ γ ， T ， c t=1 +ut （ u STAR ΔMt =准′ΔXt +θ′ΔXt G 。 12 其中 ΔXt 式，即是代表解释变量（包括和 ΔZt ECt-1 还是对辅助回归进行 LSTAR ESTAR H01、H02 ），具体步骤遵循式（ 5 - 和式（）[14]。 7 ），拒绝式（检验后，结果接受式（），所以非线性部分采用指数转换函数 6 5 标准化并利用。模型进行非线性回归，软件对 H03 等[21]的建议，我们将转换函数中的 Δyt-1 R ESTAR 根据估计结果如下： Terasvirta Δm0 t=-0.335ect-1+0.871Δyt-1-0.616Δm0 t-1+0.835Δm0 t-2+ （ -1.77 （） . 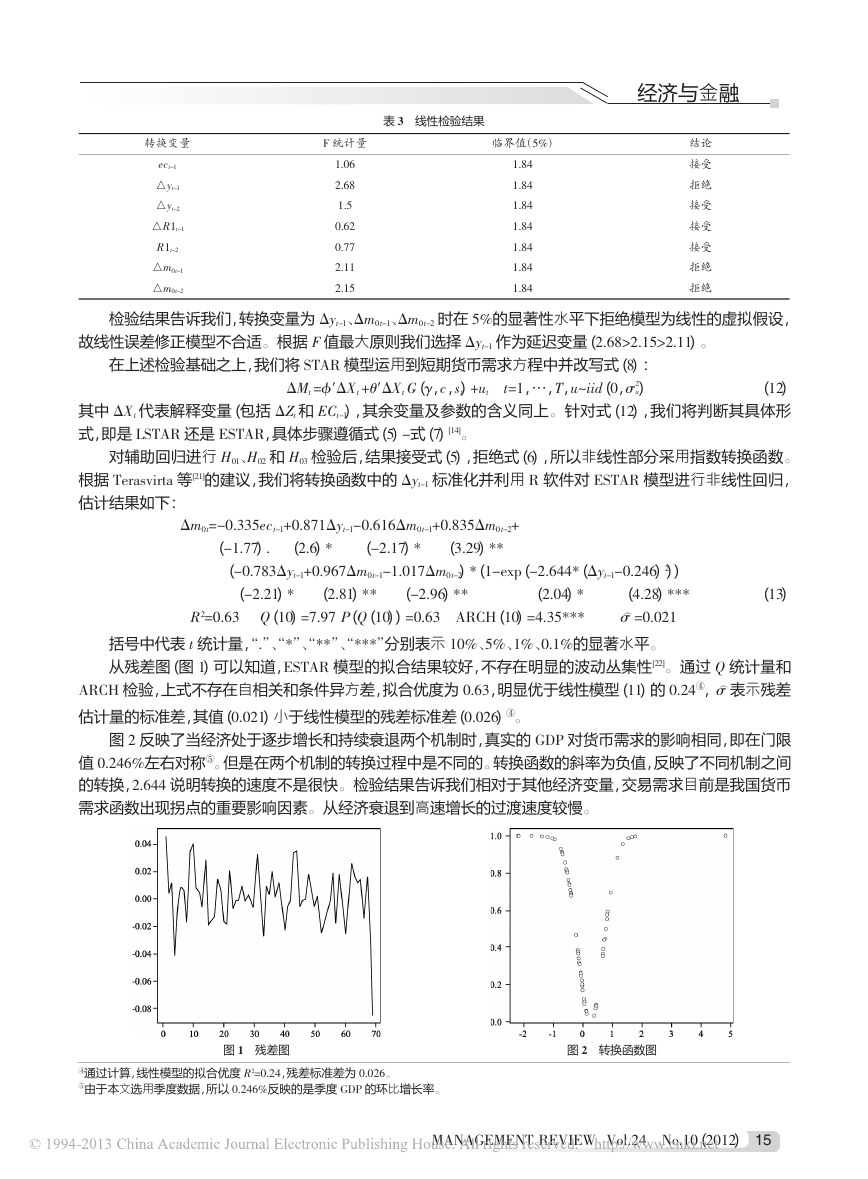（） * 2.6 （） * -2.17 -0.783Δyt-1+0.967Δm0 t-1-1.017Δm0 t-2 （）（） * ） -2.21 （ Q ） ** 2.81 （（ Q （）） -2.96 ** （ ** ） 3.29 ）（ * 1-exp （（）（ -2.644* ）（ * 2.04 Δyt-1-0.246 （ 4.28 ）2））） *** （） 13 括号中代表 t 从残差图（图 10 R2=0.63 统计量，）可以知道， 1 =7.97 P 10 =0.63 ARCH 10 =4.35*** *σ =0.021 “.”、“*”、“**”、“***” 10%、5%、1%、0.1% ESTAR 模型的拟合结果较好，不存在明显的波动丛集性[22]。的显著水平。分别表示图 ARCH 估计量的标准差，其值（）小于线性模型的残差标准差（检验，上式不存在自相关和条件异方差，拟合优度为，明显优于线性模型（）④。反映了当经济处于逐步增长和持续衰退两个机制时，真实的左右对称⑤。 2.644 对货币需求的影响相同，即在门限转换函数的斜率为负值，反映了不同机制之间检验结果告诉我们相对于其他经济变量，交易需求目前是我国货币但是在两个机制的转换过程中是不同的说明转换的速度不是很快 0.021 0.026 ）的 GDP 0.63 11 。。 2 值 0.246% 的转换，需求函数出现拐点的重要影响因素从经济衰退到高速增长的过渡速度较慢。。通过 Q 0.24④， *σ 统计量和表示残差图 1 残差图图 2 转换函数图 ④通过计算，线性模型的拟合优度 ⑤由于本文选用季度数据，所以，残差标准差为 R2=0.24 0.246% 反映的是季度 GDP 0.026。的环比增长率。 MANAGEMENT REVIEW Vol.24 No.10 2012 15 （）

两次过热和两次下滑年至年中国经济过热，实际经济与金融中国经济在样本期，经历了 “ 持两位数的增长速度，分别为 ”。1992 和软着陆和 1996 在经历了约年到从 ”。 1997 ，直到年由于受到亚洲金融危机的影响，中国经济实现了 “ 14.2%、14%、13.1%、10.9% 10%。 9.3%、7.8%、7.6%、8.4%、8.3% 9.2% 2003 投资三驾马车的拉动下，我国经济经历持续五年（约、年底由于美国金融危机爆发，全球经济下滑，我国出口量下降，实际由于在中国，收入仍然是影响人们交易的重要因素，故 “ 。两次过热和两次衰退通过梳理样本期我国的经济发展历 GDP 。2003 年之后，在出口的增长速度分别为 1997 的实际增长率长的趋势发生了较大的变化程，我们发现研究结论是与现实相吻合的消费、。2007 。最后，我们通过平均方根误差（ 24 20 年（约 2002 年才回升到 GDP 一直保个季度的高速增长后，在个季度），每年的两位数高个季度）的快速增的增长速度也开始呈递减期间我国货币需求量也 ” 10% 20 GDP 表 4 样本外预测比较 STAR 0.0206 0.0147 STAR 线性模型 0.026 0.0195 模型较线性模型具有）⑥两个指标比较误差（（ 11 MAE ）的预测能力，见表 4。通过比较两个指标， STAR 更好的预测能力。。）和平均绝对）和线性模型 RMSE 模型（ 12 STAR 标准 RMSE MAE 模型两项指标值均小于线性模型的相应指标值，故结论通过实证检验，本文得出以下几点不同于其它研究成果的结论：（）我国短期货币需求方程具有非线性效应，其具备 1 ，该结论反映了在我国经济发展的不同时期，居民对货币需求，特别是现金的持有量是不同的转换变量是滞后一期的真实国民收另外也的特点 ESTAR 。入反映了我国居民货币需求的主要动机仍然是交易需求 Δyt-1 。（）通过非嵌套检验对货币需求的机会成本变量进行实证检验，发现利率能更好的反映我国货币需求的 2 投机动机，该检验避免了对机会成本变量选取的盲目性（）尽管在样本期，利率对货币需求投机动机的影响还不显著，但随着利率市场化的进程逐步深入，金融 3 体制不断完善，相信其作用也会越来越凸显从这个意义上讲，货币需求函数的线性形式也是站不住脚的。。（）通过 4 RMSE MAE 和两项指标发现相对于传统的线性模型， ESTAR 制定和实施货币政策提供一定的参考。。。模型的预测能力更强，这将为央行参考文献： [1] Sarno, L., Peel, D., Taylor, M. Nonlinear Equilibrium Correction in US Real Money Balances, 1867-1977[J]. Journal of Money, Credit and Banking, 2003,123(35):787-799 [2] Calza, A., Zaghini, A. Non-linear Dynamics in the Euro Area Demand for M1. European Central Bank[R]. Working Paper, No.592, 2006 赫尔穆特 [3] 鲁克波尔马库斯 . , . 克莱茨希应用时间序列计量经济学[M]. . 北京机械工业出版社 : , 2008 [4] Darran Austin, Bert Ward, Paul Dalziel. The Demand for Money in China 1987-2004: A Non-Linear Modeling Approach[J]. China Economic Review, 2007,35(18):190-204 王俊非线性时间序列分析 . 孔令夷 , STAR [5] 模型及其在经济学中的应用[J]. 数量经济技术经济研究 , 2006,1(14):77-84 [6] Mehmet Canner, Bruce E. Hansen. Threshold Auto Regression with a Unit Root[J]. Econometrica, 2001,69(12):155-159 姜波克陈华证券市场和货币需求[J]. . , [7] 世界经济文汇 , 2003,1(3):14-24 [8] Sarno, L. Adjustment Costs and Nonlinear Dynamics in the Demand for Money: Italy, 1861-1991[J]. International Journal of Finance and Economics, 1999,14(42):155-177 [9] Bacon, Watts, Chan, Tong. A New Approach to the Economic Analysis of Non-stationary Time Series and the Business Cycle[J]. Econometrica, 1989,60(57):357-384 [10] Terasvirta, T. Modelling Economic Relationships with Smooth Transition Regressions. Handbook of Applied Economic Statistics[M]. 平均绝对误差，即误差绝对值的平均；均方根误差，即误差的平方和除以样本个数减一的 ⑥MAE=mean absolute error RMSE=root mean square error 平方根，计算公式：（（代表误差平方，为样本数量 Σ δ=sqrt[ n ））（ / ， di^2 ） ] di^2 n-1 。 16 （管理评论 Vol.24 No.10 2012 ）

New York: Marcel Dekker, Chapter 15, 1998 [11] Dijk, Terasvirta, Franses. Smooth Transition Autoregressive Models Survey of Recent Developments[J]. Econometric Reviews, 2002,35 经济与金融 (21):41-71 郑超愚余方 , 滕龙 . 中国货币需求函数的计量分析层次递归系统与动态调整方法[J]. : 金融研究 , 2000,122(10):13-18 , [12] [13] Van Dijk, D., Terasvirta, T., Franses, P. H. Smooth Transition Autoregressive Models———A Survey of Recent Developments[J]. 我国通货膨胀和通货紧缩的非线性转换[J]. , 彭方平 . Econometric Reviews, 2002,34(21):1-47 王少平达摩达尔薛毅谢赤古扎拉蒂统计建模与基于刘潭秋 . .N. 陈立萍 , . 戴克维 , , 软件[M]. STAR 计量经济学基础[M]. 北京 : R . [14] [15] [16] [17] 经济研究中国人民大学出版社北京清华大学出版社 : , 2007 , 2006,22(8):35-44 , 1996 模型的人民币实际汇率行为的描述[J]. 金融研究 , 2005,299(5):51-59 [18] Sarantis. Nonlinearities, Cyclical Behavior and Predictability in Stock Markets: International Evidence[J]. International Journal of Forecasting, 2001,56(17):459-482 刘柏基于赵振全 , . STAR 模型的中国实际汇率非线性态势预测[J]. 数量经济技术经济研究 , 2008,6(12):3-11 [19] [20] Gregory Chow, Yan Shen. Money, Price Level and Output in Chinese Macro Economy[R]. CEPS Working Paper, No.98, 2004 [21] Skalin, Terasvirta. Another Look at Swedish Business Cycles, 1861-1988[J]. Journal of Applied Econometrics, 1999,(14):359-378 [22] Duca, J. V., VanHoose, D. D. Recent Developments in Understanding the Demand for Money[J]. Journal of Economics and Business, 2004,67(56):247-272 A STAR-model-based Functional Research of China’s Monetary Demand (School of Economics and Management, Wuhan Sports University, Wuhan 430079) Zhang Lei Abstract: Firstly, through non-nested tests, this paper chooses interest rate as the proxy of opportunity cost of holding money and on this basis, a long-run equilibrium equation is established. After that, by application of ESTAR Model, this paper makes a nonlinear empirical test for the monetary demand in China. The result shows that the model is of significant nonlinear characteristics and the transition variable is a real reflection of national income for the next period. The conclusions above are consistent with China’s economic development. Finally, by two indicators: RMSE and MAE, this paper compares the forecasting ability between ESTAR model and the traditional linear model, and the result indicates that the ESTAR model is better. This article suggests the nonlinear model has better statistical properties than traditional linear model. Key words: monetary demand, exponential smooth transition regression, non-nested tests MANAGEMENT REVIEW Vol.24 No.10 2012 17 （）

分享到：

赞收藏

资料库

基于STAR模型的汇率预测.pdf

相关推荐

行业

热门标签

最新资料