肖明宇算法设计与分析答案.pdf-资料库

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第1页.png

第1页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第2页.png

第2页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第3页.png

第3页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第4页.png

第4页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第5页.png

第5页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第6页.png

第6页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第7页.png

第7页 / 共10页

200435b6-0d13-4a74-8265-fc2098868bd7.pdf-第8页.png

第8页 / 共10页

Design and Analysis of Algorithms (12 Spring) Due: Apr. 24, 2012 2.5  n  3 n 1. Arrange the following functions in ascending asymptotic order of growth rate: 1( ) f n 3( ) f n 解：因为 f1=O(n2.5) ， f2=2logn*2loglogn=n*logn=O(nlogn) ， f3=n1.75=O(n1.75) ， 2( ) f n  ) ， 5 ( f n  5 100  4( ) f n  2 n log 3 n n  loglog n ， 2 n 2 3.5 ，， . f4=22n=4n=O(4n)，f5=3n=O(3n)。所以可得：f20）{ maxfind(p,x); //find(p,x)从 p 中找出小于 x 的最大面值,找不到返回 p[0] xx-max，kk+1，Cmax；} 4) if(x==0) 输出 C，k，否则输出 impossible。分析：贪心算法并不一定总能找到最优的解，在某些情况下甚至不能找到一个解（例如：由面值 3，5，9 面值的币组成 10），当然在本例下总能找到解，但并不保证是最优的。方法 2（使用动态规划）：表达式：mincoin(p[i],x,result,record)= min{mincoin(p[i-1],x-t*p[i], result,record)+t, mincoin(p[i-1],x, result,record)}

//result[i][j]用于保存从面值为 p[0]--p[i]的硬币中选取凑成钱数 j+1 的最少硬币 //数，record[i][j]保存需要面值为 p[i]的硬币的数量。 1) n硬币种类数，p {1,5,10,25,100}; //初始化（p 中数值从小到大排序） 2) result[n][x]x+1，record[n][x]0; //对数组中的每个元素初始化 3) for（i=0 to n） for（j=0 to x） //均左闭右开 if(存在从面值为 p[0]--p[i]的硬币中选取凑成钱数 j+1 的最少硬币数 m) result[i][j]m, record[i][j]temp; //temp 为需要 p[i]的数量 4) if(result[n-1][x-1]>x) 则表示不能凑成 x，退出，否则接着执行 5) 输出 result[n-1][x-1]；// 输出最少钱币数 6) while(x>0){ //输出面值 7) 如果 record[n-1][x-1]大于 0，输出 record[n-1][x-1]个 p[n-1],否则转 9； 8) x=x- record[n-1][x-1]*p[n-1], n=n-1; 9) n=n-1;} 分析：该方法可以找到最优解，但是时间复杂度和空间复杂度都要比方法一大。 3. An algorithm solves problems of size n by dividing it into three subproblems of size n/2, recursively solving each subproblems, and then combine the solutions in 2n time. Can you analyze the running time of this algorithm? 解：假设用 T(n)表示解决 size 为 n 的问题所用的时间，那么解决三个 size 为 n/2 的子问题所用的时间为 3*T(n/2)，由于分治之后组合结果所用的时间为 n2，所有分治后所用的时间(假设为 F(n)) F(n)= 3*T(n/2)+ n2=MAX{O(T(n/2)), O(n2)} 4. Please using dynamic programming to solve the following knapsack problem. We are given 7 items and a knapsack. Each item i has weight of wi > 0

kilograms and value of vi > 0 dollars (given in table 1). The capacity of the knapsack is 14 kilograms. Then how to fill the knapsack to maximize the total value? Items Weight Value 1 2 3 4 5 6 7 2 3 3 1 6 3 5 3 4 2 2 7 5 6 Table 1 解：用到的数据：n----物体数量，p[n][3]-----存储 n 个物体的重量(p[i][0]),价值 p[i][1]和宝石号(p[i][2])(说明:下文中用的的数组 p 均指已经排过序，按物体重量从小到大排序，重量相同的按价值从小到大排序)，ck-----背包容量，result[n] [ck-p[0][0]+1]，record[n] [ck-p[0][0]+1]-----用到的辅助数组。result 和 record 第一维为 n，第二维为 ck-p[0][0]+1,即在有宝石 p[0]----p[i]的情况下，result[i][j] 存放背包重量为 j+p[0][0]时取得的最大价值，record[i][j]为取得最大价值时最后放进去的宝石号所在数组的组号。表达式： maxvalue(p, ck, result, record)=max{maxvalue(p-p[i], ck-p[i][0], result, record)+p[i][1], maxvalue(p-p[i], ck, result, record)}，即意思为在背包容量为 ck 中放入最大价值的宝石等于从下面两种放法中选取最大值：1.在背包中不放入某个宝石时获取的最大价值；2. 在背包中放入某个宝石时获取的最大价值。(c++实现见附件)

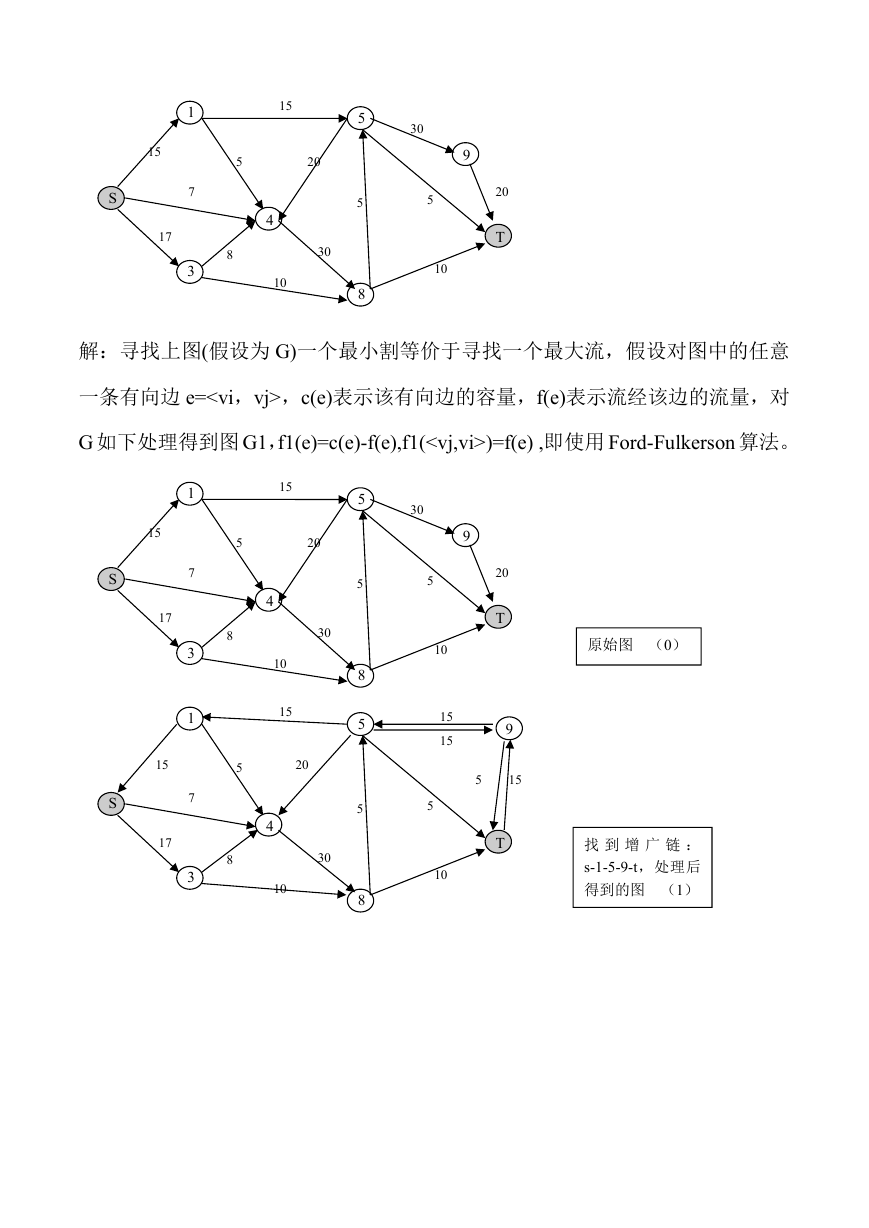
1) n宝石种类数，ck背包容量，p {宝石数据}; //初始化 2) sort p, if(ck=p[0][0]){ //输出宝石信息 7) 如果 record[n-1][ ck-p[0][0]]大于 0，输出 p[record[n-1][ ck-p[0][0]]]对应的宝石重量，宝石号，宝石价值,否则转 9； 8) ck=ck- p[record[n-1][ ck-p[0][0]]][0], n=n-1; 9) n=n-1;} 5. Find a minimum s-t cut in the following directed graph (the number beside the edge is the capacity of the edge). You are required to give the computation steps and show the size of the cut.

15 17 S1 15 5 20 8 4 1 10 30 1 1 7 3 1 5 1 5 8 1 30 5 10 9 1 20 T 解：寻找上图(假设为 G)一个最小割等价于寻找一个最大流，假设对图中的任意一条有向边 e=，c(e)表示该有向边的容量，f(e)表示流经该边的流量，对 G 如下处理得到图 G1，f1(e)=c(e)-f(e),f1()=f(e) ,即使用 Ford-Fulkerson 算法。 1 1 7 15 17 S1 3 1 1 1 7 3 1 15 17 S1 15 5 20 4 1 10 15 5 20 4 1 10 8 8 30 30 30 5 1 5 8 1 1 5 5 8 1 9 1 20 T 91 15 5 T 5 5 10 15 15 10 原始图（0）找到增广链： s-1-5-9-t，处理后得到的图（1）

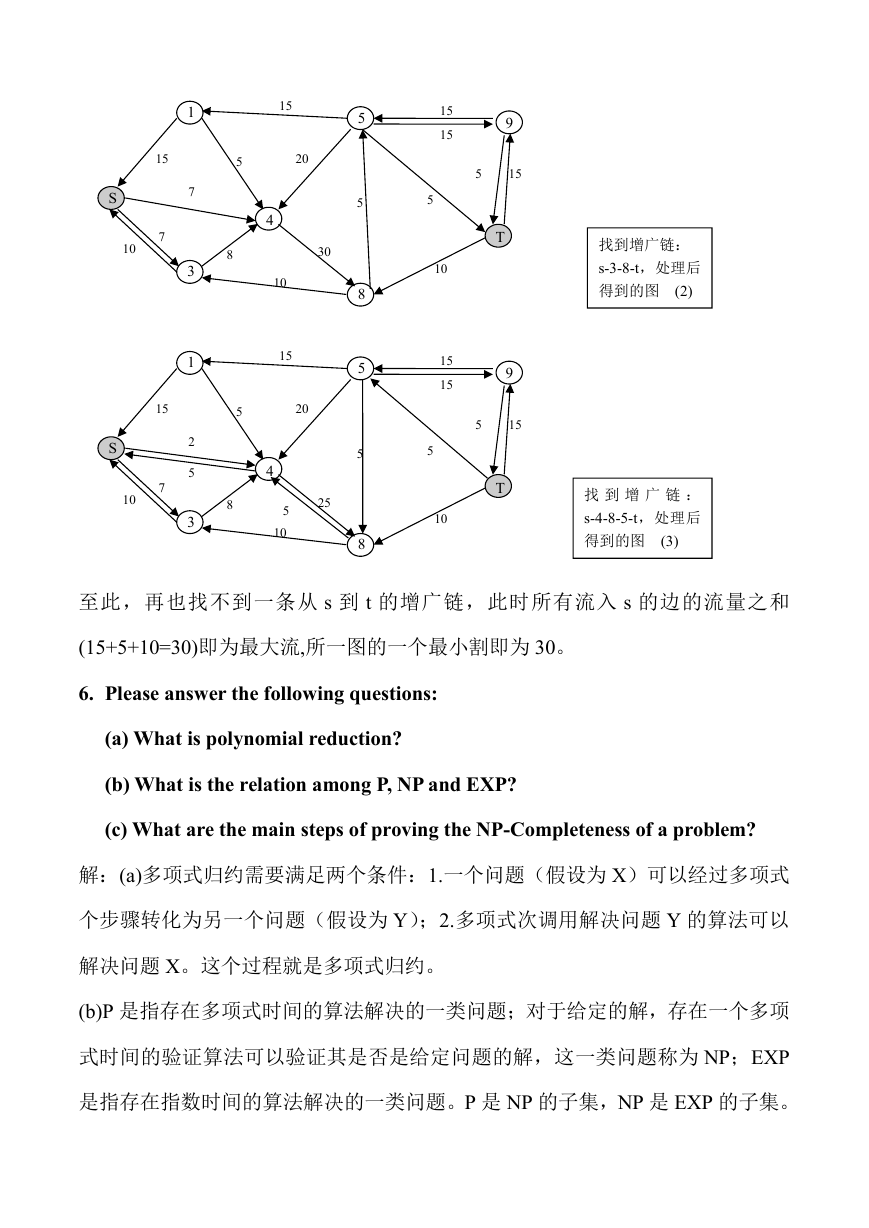
15 7 15 7 S1 10 S1 10 1 1 7 3 1 1 1 2 5 3 1 8 8 15 5 20 4 1 10 15 5 20 4 1 5 10 5 5 91 15 91 15 T T 15 15 5 10 15 15 5 10 5 1 5 8 1 5 1 5 8 1 30 25 找到增广链： s-3-8-t，处理后得到的图 (2) 找到增广链： s-4-8-5-t，处理后得到的图 (3) 至此，再也找不到一条从 s 到 t 的增广链，此时所有流入 s 的边的流量之和 (15+5+10=30)即为最大流,所一图的一个最小割即为 30。 6. Please answer the following questions: (a) What is polynomial reduction? (b) What is the relation among P, NP and EXP? (c) What are the main steps of proving the NP-Completeness of a problem? 解：(a)多项式归约需要满足两个条件：1.一个问题（假设为 X）可以经过多项式个步骤转化为另一个问题（假设为 Y）；2.多项式次调用解决问题 Y 的算法可以解决问题 X。这个过程就是多项式归约。 (b)P 是指存在多项式时间的算法解决的一类问题；对于给定的解，存在一个多项式时间的验证算法可以验证其是否是给定问题的解，这一类问题称为 NP；EXP 是指存在指数时间的算法解决的一类问题。P 是 NP 的子集，NP 是 EXP 的子集。

(c) NPC 定义：同时满足下面两个条件的问题就是 NPC 问题。1）.它是一个 NP 问题；2）.所有的 NP 问题都可以多项式归约到它。若证明一个问题是 NPC 问题可以通过两种方法来证明。方法一：按定义证明。该方法不常用。方法二：首先证明它是一个 NP 问题，再证明一个已知的 NPC 问题能多项式归约到它 7. Please prove the NP-completeness of the maximum clique problem by reducing from the maximum independent set.(In the maximum clique problem, we are given a graph and asked to find a maximum subgraph that is a complete graph.) 证明：1）.首先对于给定的一个待验证的解（假设点集为 C），首先验证所有的点组成的子图是否是完全图（在 O(n2)时间内可验证），如果是，然后验证该子图是否为最大子图，假设给定图 G 的点集为 S，那么依次把 S-C 中的每个点 si 加入到 C 中，验证 C+si 是否为完全图（同样可在 O(n2)时间内可验证）。通过上面的验证（多项式时间）即可验证 C 是否是一个正确的解，所以最大团问题是 NP 问题。 2）.此步证明最大独立集可以在多项式归约到最大团问题。证明如下：用 S 表示图 G 的顶点集，用|S|表示集合 S 的模。 a) 得到图 G 的补图 G1(可以在多项式时间内求出 G 的补图，一种算法是首先构造 S 的完全图，然后删除在 G 中的边) b) 得到图 G1 的一个最大团的点集 D。 c) 因为 D 是 G1 的一个最大团，且 G1 是 G 的补图，所以 D 是 G 的一个独立集(根据定义即可证明)。现在证明 D 是 G 的最大独立集(反证法)： a) 假设 D 不是图 G 的最大独立集，图 G 存在一个最大独立集 D1，且|D1|>|D|。 b) 由独立集定义可知 D1 中任何两个顶点之间没有边相连，那么在 G 的补图

G1 中 D1 中任何两个顶点之间都存在一条边，所以 D1 是 G1 的一个完全子图。 c) 因为|D1|>|D|，所以 G1 中存在一个大于|D|的完全子图，这与 D 是 G1 的一个最大团相矛盾，所以假设不成立，即得 D 是图 G 的最大独立集。 3）.综 1）2）可得最大团问题是一个 NPC 问题。(最大独立集是 NPC 问题) 8. Please prove that if we can check if a graph has a vertex cover of size k in polynomial time then we can also find a vertex cover of size k in polynomial time. 证明：假设图 G 的顶点集为 S，f(S，k)( true 表示存在,false 表示不存在)表示可以检测图 G 是否存在一个大小为 k 的点覆盖集。用 C，M 分别表示点集合（C 初始化为 S，M 初始化为空）。那么对于给定的 k，经过下面算法后 M 即为一个大小为 k 的点覆盖集(C-si 表示删除图中的顶点时，同样也删除与该顶点相邻的边)： 1) if(!f(C，k))直接退出,否则执行下面步骤； 2) for(对 S 中的每一个顶点 si){ //C 在处理的过程中动态变化 3) CC-si; 4) if（!f（C，k））{Msi，k--;} 5) if(0==k)break； 6) } 该算法的思想是：由于图中可能含有多个大小为 k 的点覆盖，所以需要从图中逐步删除点(删除方法任意，可以是按顶点序号删除)，直到判定图中不含有一个大小为 k 的顶点集，那么最后删除的点即是大小为 k 的点覆盖集中的一个顶点。依次循环就可以找到一个大小为 k 的点覆盖集。最多经过|s|次循环就可以找到一个大小为 k 的点覆盖集，时间为多项式时间，所以命题成立。

资料库

肖明宇算法设计与分析答案.pdf

相关推荐

课程资源

热门标签

最新资料