logo资料库

陀螺仪数据分析.docx

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：0.67M 资料格式：docx 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    MPU6050数据轻松分析
    这个文章是根据自己学习，查资料的汇总，同时把一些自己的心得加进去。如果有什么不对的，欢迎请大家指正、
    邮箱：zhb_account@163.com
    // for both classes must be in the include path of
    // specific I2C addresses may be passed as a param
    #define AX_ZERO (-1476) /* 加速度计的0偏修正值 */
    Angle+=(Gyro - Q_bias) * dt;
    Pdot[0]=Q_angle - PP[0][1] - PP[1][0];
    Angle_err = Accel - Angle;
    E = R_angle + C_0 * PCt_0;
    MPU6050 数据轻松分析 这个文章是根据自己学习，查资料的汇总，同时把一些自己的心 得加进去。如果有什么不对的，欢迎请大家指正、交流。 邮箱：zhb_account@163.com 最近看到加速度计和陀螺仪比较火，而且也有很多人都在研究。于是也在网上淘了一个 mpu6050 模块，想用来做自平衡小车。可是使用起来就发愁了。网上关于 mpu6050 的资料 的确不少，但是大家都是互相抄袭，然后贴出一段程序，看完之后还是不知道所以然。 经过翻阅各个方面的资料，以及自己的研究在处理 mpu6050 数据方面有一些心得，在这里 和大家分享一下。 在处理加速度计和陀螺仪用到的方法都是比较简单的，这里的简单并不是不需要任何基 础知识，只是这些基本知识都是最基本的，比如简单的三角函数，数学计算，物理知识，c 语言以及基本的 arduino 知识（如果不会 arduino 会其它单片机也是一样的，本文实践是使 用 arduino），如果还不具备这些知识那就快去补课吧。 1、 加速度和陀螺仪原理 当然，在开始之前至少要弄懂什么是加速度计，什么是陀螺仪吧，否则那后边讲的都是 没有意义的。简单的说，加速度计主要是测量物体运动的加速度，陀螺仪主要测量物体转动 的角速度。这些理论的知识我就不多说了，都可以在网上查到。这里推荐一篇讲的比较详细 的 文 章 《 A Guide To using IMU (Accelerometer and Gyroscope Devices) in Embedded Applications》，在网上可以直接搜索到。 2、 加速度测量 在开始之前，不知大家是否还记得加速度具有合成定理？如果不记得可以先大概了解一 下，其实简单的举个例子来说就是重力加速度可以理解成是由 x,y,z 三个方向的加速度共同 作用的结果。反过来说就是重力加速度可以分解成 x,y,z 三个方向的加速度。 加速度计可以测量某一时刻 x,y,z 三个方向的加速度值。而自平衡小车利用加速度计测出 重力加速度在 x,y,z 轴的分量，然后利用各个方向的分量与重力加速度的比值来计算出小车 大致的倾角。其实在自平衡小车上非静止的时候，加速度计测出的结果并不是非常精确。因 为大家在高中物理的时候都学过，物体时刻都会受到地球的万有引力作用产生一个向下的重 力加速度，而小车在动态时，受电机的作用肯定有一个前进或者后退方向的作用力，而加速 度计测出的结果是，重力加速度与小车运动加速度合成得到一个总的加速度在三个方向上的 分量。 不过我们暂时不考虑电机作用产生的运动加速度对测量结果的影响。因为我们要先把复 杂的事情分解成一个个简单的事情来分析，这样才能看到成果，才会有信心继续。
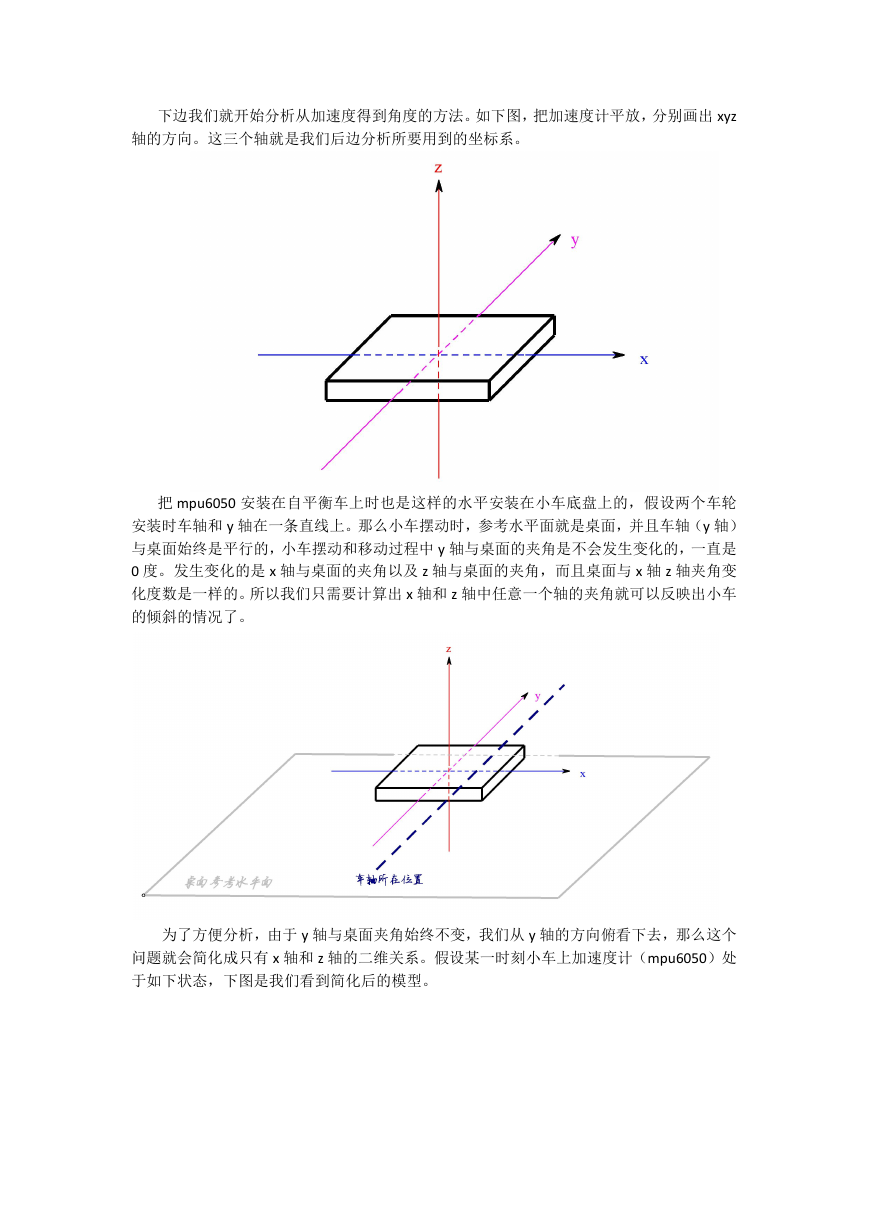
    下边我们就开始分析从加速度得到角度的方法。如下图，把加速度计平放，分别画出 xyz 轴的方向。这三个轴就是我们后边分析所要用到的坐标系。 把 mpu6050 安装在自平衡车上时也是这样的水平安装在小车底盘上的，假设两个车轮 安装时车轴和 y 轴在一条直线上。那么小车摆动时，参考水平面就是桌面，并且车轴（y 轴） 与桌面始终是平行的，小车摆动和移动过程中 y 轴与桌面的夹角是不会发生变化的，一直是 0 度。发生变化的是 x 轴与桌面的夹角以及 z 轴与桌面的夹角，而且桌面与 x 轴 z 轴夹角变 化度数是一样的。所以我们只需要计算出 x 轴和 z 轴中任意一个轴的夹角就可以反映出小车 的倾斜的情况了。 为了方便分析，由于 y 轴与桌面夹角始终不变，我们从 y 轴的方向俯看下去，那么这个 问题就会简化成只有 x 轴和 z 轴的二维关系。假设某一时刻小车上加速度计（mpu6050）处 于如下状态，下图是我们看到简化后的模型。
    在这个图中，y 轴已经简化和坐标系的原点 o 重合在了一起。我们来看看如何计算出小 车的倾斜角，也就是与桌面的夹角 a。上图 g 是重力加速度，gx、gz 分别是 g 在 x 轴和 z 轴 的分量。 由于重力加速度是垂直于水平面的，得到： 角 a+角 b=90 度 X 轴与 y 轴是垂直关系，得到： 角 c+角 b=90 度 于是轻松的就可以得出： 角 a=角 c 根据力的分解，g、gx、gz 三者构成一个长方形，根据平行四边形的原理可以得出： 角 c=角 d 所以计算出角度 d 就等效于计算出了 x 轴与桌面的夹角 a。前边已经说过 gx 是 g 在 x 轴的分量，那么根据正弦定理就可以得出： Sind=gx/g 得到这个公式可是还是得不到想要的角度，因为需要计算反正弦，而反正弦在单片机里 不是很好计算。 为了得到角度，于是又查了相关资料，原来在角度较小的情况下，角度的正弦与角度对 应的弧度成线性关系。先看看下边的图：
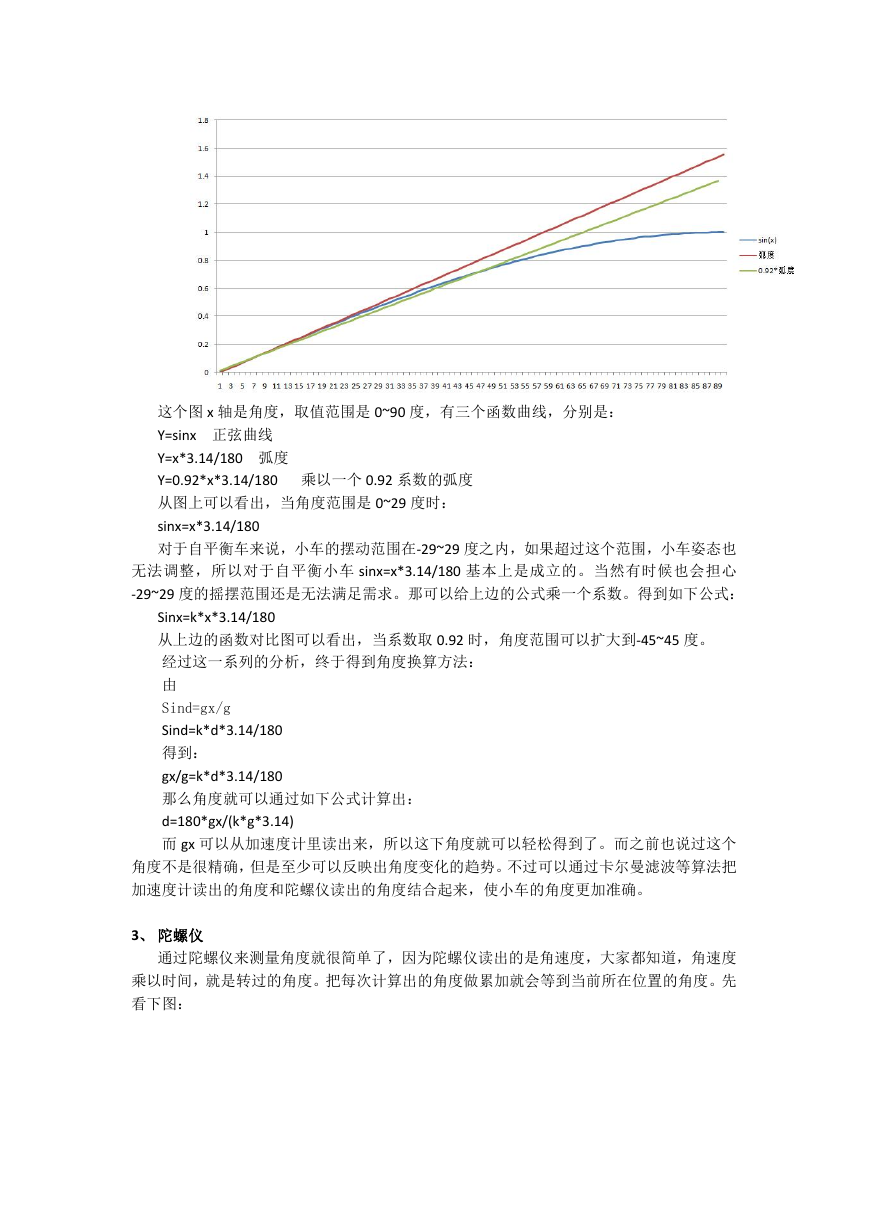
    这个图 x 轴是角度，取值范围是 0~90 度，有三个函数曲线，分别是： Y=sinx 正弦曲线 Y=x*3.14/180 弧度 Y=0.92*x*3.14/180 乘以一个 0.92 系数的弧度 从图上可以看出，当角度范围是 0~29 度时： sinx=x*3.14/180 对于自平衡车来说，小车的摆动范围在-29~29 度之内，如果超过这个范围，小车姿态也 无法调整，所以对于自平衡小车 sinx=x*3.14/180 基本上是成立的。当然有时候也会担心 -29~29 度的摇摆范围还是无法满足需求。那可以给上边的公式乘一个系数。得到如下公式： Sinx=k*x*3.14/180 从上边的函数对比图可以看出，当系数取 0.92 时，角度范围可以扩大到-45~45 度。 经过这一系列的分析，终于得到角度换算方法： 由 Sind=gx/g Sind=k*d*3.14/180 得到： gx/g=k*d*3.14/180 那么角度就可以通过如下公式计算出： d=180*gx/(k*g*3.14) 而 gx 可以从加速度计里读出来，所以这下角度就可以轻松得到了。而之前也说过这个 角度不是很精确，但是至少可以反映出角度变化的趋势。不过可以通过卡尔曼滤波等算法把 加速度计读出的角度和陀螺仪读出的角度结合起来，使小车的角度更加准确。 3、 陀螺仪 通过陀螺仪来测量角度就很简单了，因为陀螺仪读出的是角速度，大家都知道，角速度 乘以时间，就是转过的角度。把每次计算出的角度做累加就会等到当前所在位置的角度。先 看下图：
    假设最初陀螺仪是与桌面平行，单片机每 tms 读一次陀螺仪的角速度，当读了三次角速 度以后 z 轴转到上图的位置，则在这段时间中转过的角度为 x： 角 x=角 1+角 2+角 3 假设从陀螺仪读出的角速度为 w，那总角度为： X=(w1*t1+w2*t2+w3*t3)/1000 假设经过 n 次，那么总的角度如下： X=(w1*t1+w2*t2+w3*t3+…+wn*tn)/1000 实际上这就是一个积分过程。 其实这种计算出来的角度也存在一定的误差，而且总的角度是经过多次相加得到的，这 样误差就会越积累越大，最终导致计算出的角度与实际角度相差很大。于是也可以使用 卡尔曼滤波把加速度计读出的角度结合在一起，使计算出的角度更准确。 4、 mpu6050 与 arduino 连接 为了方便大家学习和复制，同时也应大家的要求，详细列出从哪里可以找到，对比了很 多觉得这个是最划算和实用的，供大家参考 名称 Mpu6050 模块 Arduino 模块 其它 来源 http://www.dwz.cn/ntW0H http://www.dwz.cn/ntY5J http://www.dwz.cn/ntYEB
    Mpu6050 可以直接买现成的模块，模块使用 i2c 接口和 arduino 通信，连接方式如下： Mpu6050 VCC GND SCL SDA Arduino VCC GND AD5 AD4 5、 Arduino 代码 在开始之前先介绍一下用到的组件和算法。Mpu6050 是通过 i2c 接口和 arduino 连接， 所以需要 i2c 库，另外 mpu6050 也有现成的库。由于陀螺仪本身就有偏差，多次积累之后偏 差会越来越大越来越不准确，所以需要用一些滤波算法来校正，这里用的是卡尔曼滤波算法。 卡尔曼滤波在网上讲的很多，这里就不多说了。网上有一个测量温度的通俗版，另外维 基百科里的介绍比较简单。有兴趣的可以去研究一下。另外也可以用其它算法来滤波，这里 也只是做演示所以不多介绍。 // Arduino Wire library is required if I2Cdev I2CDEV_ARDUINO_WIRE implementation // is used in I2Cdev.h #include "Wire.h" // I2Cdev and MPU6050 must be installed as libraries, or else the .cpp/.h files // for both classes must be in the include path of your project #include "I2Cdev.h" #include "MPU6050.h" // class default I2C address is 0x68 // specific I2C addresses may be passed as a parameter here // AD0 low = 0x68 (default for InvenSense evaluation board) // AD0 high = 0x69 MPU6050 accelgyro; int16_t ax, ay, az; int16_t gx, gy, gz; double total_angle=0; #define LED_PIN 13
    /* 把 mpu6050 放在水平桌面上，分别读取读取 2000 次，然后求平均值 */ #define AX_ZERO (-1476) /* 加速度计的 0 偏修正值 */ #define GX_ZERO (-30.5) /* 陀螺仪的 0 偏修正值 */ void setup() { // join I2C bus (I2Cdev library doesn't do this automatically) Wire.begin(); // initialize serial communication // (38400 chosen because it works as well at 8MHz as it does at 16MHz, but // it's really up to you depending on your project) Serial.begin(38400); // initialize device Serial.println("Initializing I2C devices..."); accelgyro.initialize(); // verify connection Serial.println("Testing device connections..."); Serial.println(accelgyro.testConnection() ? "MPU6050 connection successful" : "MPU6050 connection failed"); } /* 通过卡尔曼滤波得到的最终角度 */ float Angle=0.0; /*由角速度计算的倾斜角度 */ float Angle_gy=0.0; float Q_angle=0.9; float Q_gyro=0.001; float R_angle=0.5; float dt=0.01; /* dt 为 kalman 滤波器采样时间; */ char C_0 = 1; float Q_bias, Angle_err; float PCt_0=0.0, PCt_1=0.0, E=0.0; float K_0=0.0, K_1=0.0, t_0=0.0, t_1=0.0; float Pdot[4] ={0,0,0,0}; float PP[2][2] = { { 1, 0 },{ 0, 1 } }; /* 卡尔曼滤波函数,具体实现可以参考网上资料,也可以使用其它滤波算法 */ void Kalman_Filter(float Accel,float Gyro) { Angle+=(Gyro - Q_bias) * dt;
    Pdot[0]=Q_angle - PP[0][1] - PP[1][0]; Pdot[1]=- PP[1][1]; Pdot[2]=- PP[1][1]; Pdot[3]=Q_gyro; PP[0][0] += Pdot[0] * dt; PP[0][1] += Pdot[1] * dt; PP[1][0] += Pdot[2] * dt; PP[1][1] += Pdot[3] * dt; Angle_err = Accel - Angle; PCt_0 = C_0 * PP[0][0]; PCt_1 = C_0 * PP[1][0]; E = R_angle + C_0 * PCt_0; if(E!=0) { K_0 = PCt_0 / E; K_1 = PCt_1 / E; } t_0 = PCt_0; t_1 = C_0 * PP[0][1]; PP[0][0] -= K_0 * t_0; PP[0][1] -= K_0 * t_1; PP[1][0] -= K_1 * t_0; PP[1][1] -= K_1 * t_1; Angle Q_bias += K_0 * Angle_err; += K_1 * Angle_err; } void loop() { // read raw accel/gyro measurements from device double ax_angle=0.0; double gx_angle=0.0; unsigned long time=0; unsigned long mictime=0;
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料