第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
基于事件驱动的二次凸优化问题分布式优化算法.pdf
第 34 卷 第 8 期
2019 年 8月
控 制 与 决 策
and Decision
Control
Vol.34 No.8
Aug. 2019
文章编号: 1001-0920(2019)08-1635-10
DOI: 10.13195/j.kzyjc.2018.0080
基于事件驱动的二次凸优化问题分布式优化算法
赵中原, 陈 刚y
(重庆大学 自动化学院，重庆 400044)
文献标志码: A
摘 要: 针对多智能体系统中等式约束下的二次凸优化问题, 给出一种事件驱动机制下的分布式优化算法. 该算
法可以降低每个智能体控制协议的更新频率以及智能体之间的通信负担. 基于图论和李雅普诺夫函数方法给出
两种不同的事件触发条件, 其中第 2 种事件触发条件不需要拉普拉斯矩阵的最大特征根的信息, 可实现算法全分
布式实施. 两种事件触发条件均可实现算法渐近收敛到优化值, 避免智能体控制协议的连续更新以及智能体之间
的连续通信, 同时保证每个智能体相邻事件触发时刻的时间间隔大于0, 避免持续事件触发. 将所提出的算法应用
于Matlab 仿真环境中进行仿真验证, 仿真结果验证了所提出算法的有效性.
关键词: 分布式优化；多智能体系统；事件驱动；一致性；分布式算法；二次凸优化；无向图
中图分类号: TP273
Distributed event-triggered algorithm for quadratic convex optimization
problem
ZHAO Zhong-yuan, CHEN Gangy
(College of Automation，Chongqing University，Chongqing 400044，China)
Abstract: This paper investigates the quadratic convex optimization problem with equality constraint for multi-agent
systems (MASs). In order to reduce the controllers’ update frequency and the communication burden among agents,
a distributed event-triggered optimization algorithm is proposed. Based on the graph theorem and Lyapunov function
method, two different event-triggered conditions are designed, which guarantee that agents can asymptotically converge
to their optimal values. Especially, the second event-triggered condition dose not require the information of the largest
eigenvalue of the Laplacian matrix, and thus the algorithm can be implemented in a fully distributed way. The continuous
update of controllers and the continuous communication among agents are not required. Meanwhile, the interval of any
two contiguous event trigger instants of each agent is more than zero, and continuous event triggering is avoided. Finally,
the proposed algorithm is verified in the Matlab simulation environment, and the result of numerical simulation shows
the effectiveness of the proposed algorithm.
Keywords: distributed optimization；multi-agent system；event-triggered；consensus；distributed algorithm；quadratic
convex optimization；undirected graph
0
优化问题也得到了广泛的关注.
多智能体系统应用广泛, 如多机器人编队系统、
智能交通系统、微电网分布式控制与优化调度等[1-5],
因此围绕多智能体系统的分布式协调控制与决策问
题受到越来越多研究者的广泛关注与研究[6]. 一致性
问题是分布式控制与决策问题中的一个基础研究问
题,其目标是使得一智能群体仅通过各自与自己邻居
之间的局部信息交换实现整体系统的一致性. 当进
一步考虑到多智能体系统代价或成本函数时,分布式
分布式优化问题的目标是用分布式算法实现系
统目标函数的最小化或者最大化, 例如微电网中的
优化调度问题、优化投资问题和资源的优化分配问
题. 系统的目标函数通常是系统中每个智能体的目
标函数之和. 在多智能体协调算法的启发下, 分布式
优化方法得到了广泛的研究和应用[7-19]. 分布式优化
算法大致可分为两类: 连续算法[10-11,16-18] 和离散迭
代算法[7-9,12-15]. 文献 [19] 给出了两种分布式混杂算
收稿日期: 2018-01-16；修回日期: 2018-07-05.
基金项目: 国家自然科学基金项目(61673077, 61273108)；重庆市基础与前沿研究计划项目(CSTC2016jcyjA0361)；
中央高校基本科研业务费项目(106112017CDJQJ178827).
责任编委: 董久祥.
y
通讯作者. E-mail: chengang@cqu.edu.cn.
1636
控 制 与 决 策
第34卷
法以解决无线网络中的优化聚类问题. 上述文献中
的方法需要智能体连续地或者快速周期性地更新控
制并进行相邻节点间的通信. 在实际多智能体系统
中, 每个智能体通常采用嵌入式数字微控制器, 其能
量存储、计算能力和通信能力均有限, 因此高速的运
行和通信对实际系统依然是一种挑战. 然而, 事件驱
动算法可以在很大程度上减少计算负担和通信负担,
并且能有效降低系统的功耗[20]. 受文献[20] 启发, 文
献[21-22] 将事件驱动机制应用于求解多智能体一阶
系统一致性问题, 有效减少了控制器的更新次数, 然
而邻居节点之间仍需连续通信; 文献[23] 针对多智能
体系统的聚合问题,利用联合测量方法设计了事件触
发条件并有效避免了对邻居状态的连续检测,进而避
免了邻居间的连续通信; 文献[24] 提出了一种自适应
一致性算法,并采用事件触发的通信策略有效解决了
连续通信的问题.
凸优化问题分布式算法的设计本身就是一个复
杂的问题,现有的成果多是分布式连续算法或者周期
迭代离散算法. 结合事件驱动方法来设计凸优化问
题的分布式事件驱动算法, 既要解决凸优化问题, 又
要最大程度地降低控制器输出的更新频率以减少控
制器的功耗,同时还要减少智能体系统对通信网络带
宽的要求, 即降低智能体之间的数据通信量. 在多个
控制目标下,凸优化问题的分布式事件驱动算法设计
相较于分布式连续算法或者周期迭代离散算法的设
计更加困难. 目前, 基于事件驱动机制的分布式优化
算法的相关成果还很有限[25-27], 文献[25-27] 研究了
无约束下的优化问题.
受文献 [23-24] 启发, 本文针对含有等式约束的
二次凸优化问题, 给出一种分布式事件驱动算法, 采
用李雅普诺夫函数方法设计两种不同的事件触发条
件. 不同于连续优化算法以及离散迭代算法, 本文的
算法可有效地降低控制器的更新次数以及邻居间的
通信次数. 从理论上证明算法渐近收敛于优化解, 且
保证每个智能体相邻事件触发时刻的时间间隔大于
0,不会持续事件触发.
1 备知及问题描述
1.1 代数图论
多智能体系统可以由图 G = (V; E; A) 来描述.
其中: V = fv1; v2; ; vng 为智能体节点集合; E 2
fV V g 为边的集合, (vi; vj) 2 E 表示节点 j 可以
接收到节点 i 的信息; 矩阵 A 2 Rnn 为图 G 的邻
接矩阵. 如果 (vi; vj) 2 E, 则 A 的元素 aij = 1, 否
n∑
则 aij = 0. 本文不考虑存在自环的情况, 因此 aii =
0. 图的入度矩阵 D 定义为diagfd1; d2; ; dng, 其中
aij. 矩阵 L = [lij]nn 为图 G 的拉普拉斯
di =
∑
j=1
i̸=j
矩阵, 它的对角元素为 lii =
aij, 非对角元素为
lij = aij. 邻接矩阵 A、入度矩阵 D 与拉普拉斯矩
阵L之间满足L = D A.
对于无向图 G; (vi; vj) 2 E 代表 (vj; vi) 2 E 也
成立, 同时 aij = aji = 1. 因此, 无向图的邻接矩阵
A 和拉普拉斯矩阵 L 均为对称矩阵. 无向图中, 如果
两个不同节点间存在一条路径相连, 则称两个节点
是连通的. 如果任意两个不同节点均是连通的, 则称
图是连通图. 如果图 G 是连通的, 则 0 是拉普拉斯矩
阵 L 的简单特征根. 矩阵 L 的最大特征根 n(L) 满足
n(L) < 2dmax, 其中 dmax = maxfdi; i = 1; 2; ;
ng且dmax ⩽ n 1.
1.2 问题描述与分析
本文研究如下等式约束下的二次凸优化问题:
n∑
n∑
i=1
min
s:t:
fi(zi);
zi = D:
i=1
(1)
(2)
n∑
其中: fi(zi)为智能体 i的成本函数, zi 为智能体 i成本
函数fi(zi)的自变量;式(2)为等式约束, D =
Di.
假设1 多智能体系统中, 智能体 i 仅可获取其
i=1
自身私有信息fi(xi(t))和Di.
假设2 假设fi(zi)为二次凸函数,即
fi(zi) = iz2
i + izi + i;
(3)
其中i; i; i 为智能体i的成本参数且均为正常数.
对于优化问题(1) 和(2), 存在很多种传统集中式
求解方法. 然而, 集中式控制需要一个中央控制器控
制整个系统,同时需要更加复杂的通信网络来获取系
统的全局信息. 中央控制器一旦出现故障会导致整
个系统崩溃, 也不利于系统的扩展. 相较于集中式控
制, 分布式控制就有较好的可靠性和可扩展性. 由于
分布式系统中每个智能体都装备了一个控制器,系统
不再需要中央控制器,使得系统不会因为个别智能体
故障影响到整个系统, 具有更好的可靠性; 同时智能
体之间只需与邻居间进行局部信息交换就可以实现
整体的控制目标, 不再需要系统的全局信息, 因此系
统避免了复杂通信网络,同时也增强了系统的可扩展
性. 因此, 本文的目标是通过设计分布式事件驱动一
第8期
赵中原 等: 基于事件驱动的二次凸优化问题分布式优化算法
1637
致性算法求解优化问题(1)和(2).
2.2 事件触发条件1
基于拉格朗日乘子法可以得到问题(1) 和(2) 的
设计事件触发函数为
一个等价解集,即
@f1(z1)
@z1
步得到
=
@f2(z2)
@z2
= =
@fn(zn)
@zn
;
=
(4)
其中
其中
为对应于优化解集的正常数. 由式(3) 可进一
φi(t) = jei(t)j wi(t):
ei(t) = ^i(t) i(t); t 2 [ti
n∑
k; ti
k+1);
aij( ^i(t) ^j(t))
:
wi(t) = i
21z1 + 1 = = 2nzn + n =
由式(2)和(5)可得
=
对应的优化值z
i 为
D +
n∑
n∑
i=1
1
2i
i=1
i
2i
;
i =
z
i
2i
:
:
(5)
(6)
(7)
本文的目标是设计分布式事件驱动算法求解出
问题(1)和(2)的优化解z
i .
2 要结果
定义变量 xi(t) 和变量 i(t), 其中 xi(t) 是对问题
(1) 和(2) 的优化解 z
i 的估计变量, 且满足 xi(0) = Di.
变量 i(t) 定义为 i(t) ∆= 2ixi(t) + i. 由式(5) 可得,
当下式成立时, xi(t) = z
i :
1(t) = 2(t) = = n(t) =
:
(8)
由 式 (8) 可 知, 问 题 (1) 和 (2) 可 以 转 化 为 关 于
i(t)的一致性问题.
2.1 控制算法
对于每个智能体定义一个事件触发函数 φi(t)，
k(k = 1; 2; ) 为 φi(t) > 0 对应的时
事件触发时刻 ti
刻. 因此, 每个智能体事件触发时刻为一个单调递增
的时间点列,即ti
k; ; k 2 N.
0; ti
本文设计的优化算法如下:
1; ; ti
n∑
_i(t) = 2i
aij( ^i(t) ^j(t));
j=1
i(0) = 2ixi(0) + i:
(9)
(10)
其中: ^i(t) 为当前最新事件触发时刻的状态值, aij 为
多智能体系统通信拓扑图对应邻接矩阵A的元素.
令 (t) = [1(t); 2(t); ; n(t)]T; ^(t) = [ ^1(t);
^2(t); ; ^n(t)]T; K = diagf21; 22; ; 2ng.
式(9)可进一步写成
_(t) = KL ^(t):
(11)
j=1
n∑
j=1
(
n∑
2i
j=1
i
i=1
i=1
1
4i
_V (t) =
n∑
由 _i = _i(t) _
n∑
n∑
_V (t) = n∑
n∑
进而有
i=1
i=1
)
(i(t)
n∑
i(t)
n∑
i=1
j=1
aij( ^i(t) ^j(t)) =
aij( ^i(t) ^j(t)):
aij( ^i(t) ^j(t))+
j=1
aij( ^i(t) ^j(t)):
这里 i 为待设计的正参数.
j=1
事件触发条件为
φi(t) > 0:
智能体 i 检测事件触发条件(15) 是否成立, 若不
成立, 则没有进一步动作, 反之智能体 i 触发事件, 此
刻智能体 i 更新触发时刻状态值并发送给其邻居节
点, 同时更新自己的控制律并将 ei(t) 设置成 0, 智能
体 i 的邻居节点接收到智能体 i 最新触发时刻状态值
并更新自己的控制律. 因此, 每个智能体只在自己及
其邻居事件触发时刻更新控制律并进行通信.
定理1 假设图 G 为无向连通图. 如果参数 i 满
(i = 1; 2; ; n), 则算法(9) 和(10) 在
足 i <
事件触发条件(15)下可以求解优化问题(1)和(2).
n(L)
1
证明 定义变量 i(t) = i(t)
, 构造李雅普
诺夫函数
V (t) =
1
4i
2
i (t):
显然V (t) ⩾ 0. 当且仅当i(t) =
时V (t) = 0.
对V (t)求导可得
n∑
i=1
n∑
_V (t) =
1
4i
= _i(t)可得
i=1
n∑
2i
2i
_i:
)
aij( ^i(t) ^j(t))
=
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
1638
控 制 与 决 策
第34卷
由于图G为无向连通图,由L矩阵的对阵性可得
n∑
n∑
_V (t) = n∑
j=1
i=1
由式(20)可知, (19)可转化为
aij( ^i(t) ^j(t)) = 0:
n∑
i(t)
aij( ^i(t) ^j(t)):
(20)
(21)
i=1
j=1
将式(21)写成向量形式
_V (t) = T(t)L ^(t):
由式(13)可知, (22)可表示为
_V (t) = ( ^(t) e(t))TL ^(t);
其中e(t) = [e1(t); e2(t); ; en(t)]T. 进而可得
_V (t) = ^T(t)L ^(t) + eT(t)L ^(t):
由于 ^T(t)LL ^(t) ⩽ n(L) ^T(t)L ^(t),且有
(23)
(24)
(22)
由式(14)和(31)可知
其中 ∆i =
1
2n(L)
1
i
n(L) 2
. 当 ∆i > 0 时, _V ⩽
时, _V ⩽ 0. 由拉塞尔不变集原
2
0. 因此当 i <
理可以得到当 _V = 0 时,有
n(L)
^1(t) = ^2(t) = = ^n(t) = c;
其中c为未知常数. 由式(13)和(31),可得
e1(t) + 1(t) = = en(t) + n(t) = c:
(31)
(32)
wi(t) = 0:
(33)
由式(12) 以及条件 φi(t) ⩽ 0 可得 ei(t) = 0. 由式(31)
可知,当时间t ! 1时,有
n∑
1(t) = 2(t) = = n(t) = c:
由式(9)可得
(34)
w
w
aij( ^i(t) ^j(t))d:
(35)
t
1
2i
_i( )d =
t
0
eT(t)L ^(t) ⩽ a
2
eT(t)e(t) +
1
2a
其中a为正常数,可以得到
^T(t)LL ^(t);
(25)
0
对式(35)两边求和可得
;
(30)
进一步可得
i=1
_V (t) ⩽ 1
^T(t)LL ^(t) +
n(L)
^T(t)LL ^(t):
1
2a
eT(t)e(t)+
a
2
(26)
选择a = n(L),可得
_V (t) ⩽ 1
2n(L)
由 ^T(t)LL ^(t) =
^T(t)LL ^(t) +
n(L)
eT(t)e(t):
2
( n∑
n∑
aij( ^i(t) ^j(t))
( n∑
n∑
j=1
i=1
)2
aij( ^i(t) ^j(t))
(27)
可得
)2
+
(28)
_V (t) =
2n(L)
1
n∑
n(L)
2
i=1
i=1
j=1
e2
i (t):
当事件触发条件(15) 不满足(即 φi(t) ⩽ 0) 时, 可
得
jei(t)j ⩽ i
j=1
将式(29)代入(28),可得
_V (t) =
1
2n(L)
:
n∑
aij( ^i(t) ^j(t))
( n∑
n∑
( n∑
n∑
( n∑
2
i
aij( ^i(t) ^j(t))
∆i
j=1
j=1
i=1
i=1
)2
aij( ^i(t) ^j(t))
aij( ^i(t) ^j(t))
=
(29)
+
)2
)2
2
n(L)
n∑
i=1
j=1
_i( )d =
aij( ^i(t) ^j(t))d =
aij( ^i(t) ^j(t))d :
t
t
t
0
0
0
i=1
i=1
i=1
j=1
j=1
j=1
1
2i
n∑
w
n∑
n∑
w
n∑
n∑
w
n∑
n∑
n∑
i(t) n∑
n∑
n∑
1
2i
1
2i
1
2i
i(t) =
j=1
i=1
i=1
i=1
t
0
n∑
由式(38)可得
i=1
由式(10)可得
n∑
i=1
1
2i
由式(34)和(40)可得
由矩阵L的对称性可得
aij( ^i(t) ^j(t)) = 0:
w
由式(36)和(37)可得
i=1
_i( )d = 0:
lim
t!1 i(t) =
i=1
xi(0) +
n∑
i
2i
:
(2ixi(0) + i):
n∑
i=1
1
2i
(36)
(37)
(38)
(40)
(41)
1
2i
i(0) = 0:
(39)
第8期
赵中原 等: 基于事件驱动的二次凸优化问题分布式优化算法
D +
n∑
n∑
i=1
1
2i
i=1
i
2i
i
2i
:
lim
t!1 i(t) = c =
=
由i(t) ∆= 2ixi(t) + i 可得
lim
t!1 xi(t) = x
i (t) =
定理1证明完毕.2
n∑
于任意时间t,有
xi(t) = D;
i=1
:
(42)
即
当
n∑
j=1
aij( ^i(ti
k′)) = 0时,有
⩾ i
2i
> 0:
k
ti
ti
k+1
k) ^j(tj
n∑
= 0:
(43)
jei(t)j i
aij( ^i(ti
k) ^j(tj
k′))
j=1
因此,智能体i不会触发事件.
2) 在 [ti
k; ti
k+1) 时间内, 智能体 i 的邻居节点有事
件触发. 例如智能体j 的事件触发时刻为tj
k′,则有
(44)
k′ ti
tj
k > 0;
1639
(50)
(51)
(52)
注1 由式(39) 和 i(t) ∆= 2ixi(t) + i 可得, 对
即算法可以保证系统实时满足等式约束.
注2 从上述证明分析过程中可以看出, 本文算
法需要利用拉普拉斯矩阵 L 的对称性, 因此本文算法
(9)和(10)仅适用于通信网络为无向连通图的情况.
定理 2 假设图 G 是无向连通图, 对于智能体
i(i = 1; 2; ; n), 事件触发条件(15) 可以保证其任
k > 0, 即智能体
意两个连续的事件触发时刻 ti
i不会持续事件触发.
ti
k+1
证明 分两种情况进行讨论.
1) 在 [ti
事件触发,即
k; ti
k+1) 时间内, 智能体 i 的邻居节点没有
jei(t)j ⩽ i
k 时,jei(ti
恒成立. 当t = ti
k+1)j > i
jei(ti
k) ^j(tj
aij( ^i(ti
k)j = 0. 当t = ti
k) ^j(tj
aij( ^i(ti
k′))
k′))
(45)
k+1 时,有
n∑
n∑
j=1
j=1
由式(9)和(13)可得
djei(t)j
n∑
dt
2i
⩽ j _ei(t)j = j _i(t)j =
aij( ^i(ti
k) ^j(tj
k′))
:
j=1
aij( ^i(t) ^j(t)) ̸= 0时,有
n∑
w
j=1
当
djei( )j
ti
k+1
dt
ti
k)
ti
k
(ti
k+1
因此有
ti
k
⩾
ti
k+1
j=1
d ⩽
2i
n∑
n∑
2i
n∑
i
j=1
j=1
aij( ^i(ti
k) ^j(tj
k′))
aij( ^i(ti
k) ^j(tj
k′))
aij( ^i(ti
k) ^j(tj
k′))
:
:
;
(46)
(47)
(48)
(49)
然后可得
ti
ti
k+1
k > 0:
(53)
在第1) 种情况下, 智能体 i 的相邻触发时刻的下
i
, 因此第1) 种情况下智能体 i 不可能持续事
界为
2i
件触发. 要使智能体 i 持续事件触发只可能在邻居事
件触发状态的影响下发生. 通过反证法证明在邻居
事件触发状态的影响下也不会出现智能体 i 持续事
件触发现象.
假设智能体 i 受邻居触发状态影响持续事件触
k(k = 0; 1; ). 在触发时刻 t =
发, 触发时刻为 t = ti
k 可能存在两种情形: i) !i(ti
ti
k) = 0; ii) !i(ti
k; ti
k) = 0 时, 可知当 t 2 [ti
k) ̸= 0.
i) 当 !i(ti
k+1) 时, 有
aij( ^i(t) ^j(t)) = 0, 进而得到 _i(t) = 0. 因此
k+1, 有
n∑
ei(t) 0; t 2 [ti
je(ti
k+1)j > !i(ti
n∑
ii) 当 !i(ti
k+1) 时, 有
aij( ^i(t) ^j(t))̸= 0, 进而得到 _i(t) ̸= 0. 在下一
k+1). 在下一触发时刻 t = ti
k+1) = 0矛盾.
k; ti
k+1) ⩾ 0,即与e(ti
k) ̸= 0 时, 可知当 t 2 [ti
k; ti
j=1
j=1
触发时刻t = ti
w
k+1,当!i(ti
djei( )j
ti
k+1
k+1) > 0时,有
d > !i(ti
k+1):
ti
k
dt
(54)
k
ti
为保证式(54) 成立, 必存在一个严格正的常数 "i 使得
⩾ "i > 0. 然而, 存在严格正的常数 "i 与假
ti
k+1
设存在智能体 i 持续事件触发矛盾. 在下一触发时刻
t = ti
k) = 0时的情况
一致, 可得出 t = ti
k+2 时刻智能体 i 不会出现智能体 i
持续事件触发, 因此与假设智能体 i 持续事件触发矛
盾.
k+1) = 0时,即与!i(ti
k+1,当!i(ti
综合上述分析, 智能体 i(i = 1; 2; ; n) 任意两
k > 0, 智能体 i 不会
个连续的事件触发时刻 ti
ti
k+1
持续事件触发.2
注3 由定理1 可知, 参数 i 的上界与矩阵 L 的
1640
控 制 与 决 策
最大特征根 n(L)有关. 由拉普拉斯矩阵的性质可知
n(L)满足n(L) ⩽ 2dmax ⩽ 2(n 1),因此可以得到
i <
2.3 事件触发条件2
2(n 1)
1
.
定义一个新的事件触发函数以避免智能体对全
局信息的需要. 新的事件触发函数如下:
′
i(t) = e2
φ
i (t) w2
i ;
其中
wi =
vuut
′
i
n∑
aij( ^i(t) ^j(t))
2
;
(55)
(56)
j=1
这里
′
i 为待设计的正参数.
触发条件为
′
φ
i(t) > 0:
(57)
′
i 满
; i = 1; 2; ; n, 则算法(9) 和(10) 在事件
定理3 假设图 G 为无向连通图. 如果参数
′
i <
足
触发条件(57)下,可以求解优化问题(1)和(2).
1
4di
证明 构造与定理1 相同的李雅普诺夫函数. 由
式(24)可得
_V (t) = ^T(t)L ^(t) + eT(t)L ^(t) =
aij( ^i(t) ^j(t))
n∑
2
+
n∑
n∑
n∑
j=1
1
2
n∑
i=1
1
2
n∑
i=1
1
2
n∑
i=1
i=1
j=1
ei(t)
aij( ^i(t) ^j(t)) =
aij( ^i(t) ^j(t))
n∑
n∑
aijei(t)( ^i(t) ^j(t)) ⩽
n∑
n∑
j=1
j=1
i=1
+
2
aij( ^i(t) ^j(t))
n∑
n∑
2
+
i=1
j=1
die2
i (t)
2b
b
2
+
i=1
j=1
其中b为满足b < 1的正常数. 进一步可得
_V (t) ⩽ 1
n∑
2
i=1
(1 b)
die2
i (t)
2b
:
n∑
n∑
i=1
j=1
n∑
n∑
i=1
j=1
由触发函数(55)和触发条件(57)可得
_V (t) ⩽ 1
2
(1 b)
aij( ^i(t) ^j(t))
aij( ^i(t) ^j(t))
2
;
(58)
aij( ^i(t) ^j(t))
2
+
n∑
i=1
1
2
′
di
2b
n∑
i=1
n∑
aij( ^i(t) ^j(t))
n∑
j=1
第34卷
2 ⩽
′
∆
i
aij( ^i(t) ^j(t))
2
;
(60)
j=1
′
i
其中∆
′
i <
. 当∆
′
i > 0时, _V (t) ⩽ 0,即当
i = 1 b di
′
b(b 1)
由于 0 < b < 1, 容易得到当 b = 0:5 时, b(1 b)
时, _V (t) ⩽ 0.
di
b
:
取最大值0.25. 因此可得
′
i <
1
4di
(61)
后续的证明过程类似于定理1的证明过程.2
定理 4 假设图 G 是无向连通图. 对于智能体
i(i = 1; 2; ; n), 事件触发条件(57) 可以保证其任
k > 0, 即智
意两个连续的事件触发时刻满足 ti
能体i不会持续事件触发.
ti
k+1
证明 下面同样分两种情况进行讨论.
1) 在 [ti
事件触发, 即
k+1) 时间内, 智能体 i 的邻居节点没有
k; ti
i (t) ⩽
e2
恒成立. 当t = ti
e2
i (ti
k+1) >
(62)
k) ^j(tj
2
aij( ^i(ti
k′))
k)j = 0. 当t = ti
k) ^j(tj
aij( ^i(ti
2
k′))
:
k+1 时,有
′
i
j=1
n∑
n∑
k 时,jei(ti
′
i
vuut n∑
j=1
′
i
j=1
√
aij( ^i(ti
k) ^j(tj
2
k′))
由式(62)可得
k+1)j ⩽
jei(ti
由式(9)和(13)可得
djei(t)j
n∑
dt
⩽ j _ei(t)j = j _i(t)j =
aij( ^i(ti
k) ^j(tj
k′))
:
n∑
当
j=1
j=1
aij( ^i(t) ^j(t)) ̸= 0时,有
2i
n∑
(63)
:
(64)
(65)
aij( ^i(ti
k) ^j(tj
2
k′))
> 0:
(66)
j=1
由式(65)可得
w
djei( )j
ti
k+1
d ⩽
n∑
2i
dt
ti
k)
(59)
ti
k
(ti
k+1
+
进一步,由触发条件(57)可得
j=1
2
:
aij( ^i(ti
k) ^j(tj
k′))
(67)
vuut n∑
√
2i
n∑
j=1
′
i
j=1
j=1
1
di
n∑
( n∑
√
2i
′
i
di
⩾
j=1
n∑
n∑
j=1
第8期
ti
k
⩾
ti
k+1
由
可得
ti
k
ti
k+1
即
n∑
当
aij( ^i(ti
k) ^j(tj
k′))
2 ⩾
aij( ^i(ti
k) ^j(tj
k′))
)2
;
aij( ^i(ti
k) ^j(tj
k′))
aij( ^i(ti
k) ^j(tj
k′))
√
j=1
ti
k
⩾
ti
k+1
′
i
4di2
i
> 0:
k) ^j(tj
k′)) = 0时,有
j=1
aij( ^i(ti
jei(t)j 0;
√
vuut n∑
′
i
aij( ^i(ti
k) ^j(tj
k′))
2 ⩾ 0:
赵中原 等: 基于事件驱动的二次凸优化问题分布式优化算法
1641
aij( ^i(ti
k) ^j(tj
2
k′))
aij( ^i(ti
k) ^j(tj
k′))
> 0;
(68)
(69)
(70)
(71)
(72)
(73)
图 1 通信拓扑图
表 1 函数 fi(xi) 的成本参数
Agenti
i
i
i
1
0.096
1.22
51
2
0.072
3.41
31
3
0.105
2.53
78
4
0.082
4.02
42
n∑
令初始值 x1(0) = D1 = 130; x2(0) = D2 =
90; x3(0) = D3 = 80; x4(0) = D4 = 100; D =
Di = 400,则对应的1(0) = 26:18; 2(0) = 16:37;
i=1
3(0) = 19:33; 4(0) = 20:42. 由式 (6) 和 (7) 可知,
对应的优化解
4 (t) =
1 (t) =
2 (t) =
1(t) = z
1 = 99:249 6; x
2(t) = z
2 =
4(t) = z
4 =
3 = 84:504 4; x
3(t) = z
3 (t) =
= 20:275 9; x
117:124 5; x
99:121 5.
由图1 可知, 系统对应的拉普拉斯矩阵的最大特
征根 n(L) = 4, 由定理 1 可以得到 i 需满足 i <
0:25,因此设置 1 = 2 = 3 = 4 = 0:24. 仿真结果
如图2 图9所示.
j=1
因此,智能体i不会触发事件.
2) 在 [ti
k; ti
k+1) 时间内, 智能体 i 的邻居节点有触
发事件,例如智能体j 事件触发时刻为tj
k′,则有
k′ ti
tj
k > 0:
进而可得
(74)
图 2 i(t) 的收敛过程( 1; 2; 3; 4 = 0:24)
ti
ti
k+1
k > 0:
(75)
接下来的证明过程与定理2 相同, 此处省略. 同
样可以得出, 智能体 i(i = 1; 2; ; n) 任意两个连续
件触发.2
k > 0, 智能体 i 不会持续事
的事件触发时刻 ti
ti
k+1
3 仿真实验
通过Matlab 仿真来验证本文算法以及两种事件
触发条件的有效性.
考虑由4 个智能体组成的多智能体系统, 智能体
之间的通信拓扑图如图1所示.
每个智能体成本函数 fi(zi) 为二次凸函数, 其对
应的参数如表1所示.
图 3 je1(t)j 和 w1(t) 的轨迹
图 4 je2(t)j 和 w2(t) 的轨迹
124305101520t/s30252015ξiξ1ξ2ξ3ξ405101520t/s420|eω11|,ω1|e1|05101520t/s420|eω22|,ω2|e2|
1642
控 制 与 决 策
第34卷
较少.
n∑
n∑
图 8 和 图 9 分 别 给 出 了 xi(t) 的 收 敛 曲 线 以 及
xi(0) 的曲线. 可以看出, xi(t) 收敛到各
xi 和
i=1
自的优化值,同时等式约束也实时得到了满足.
i=1
′
1 =
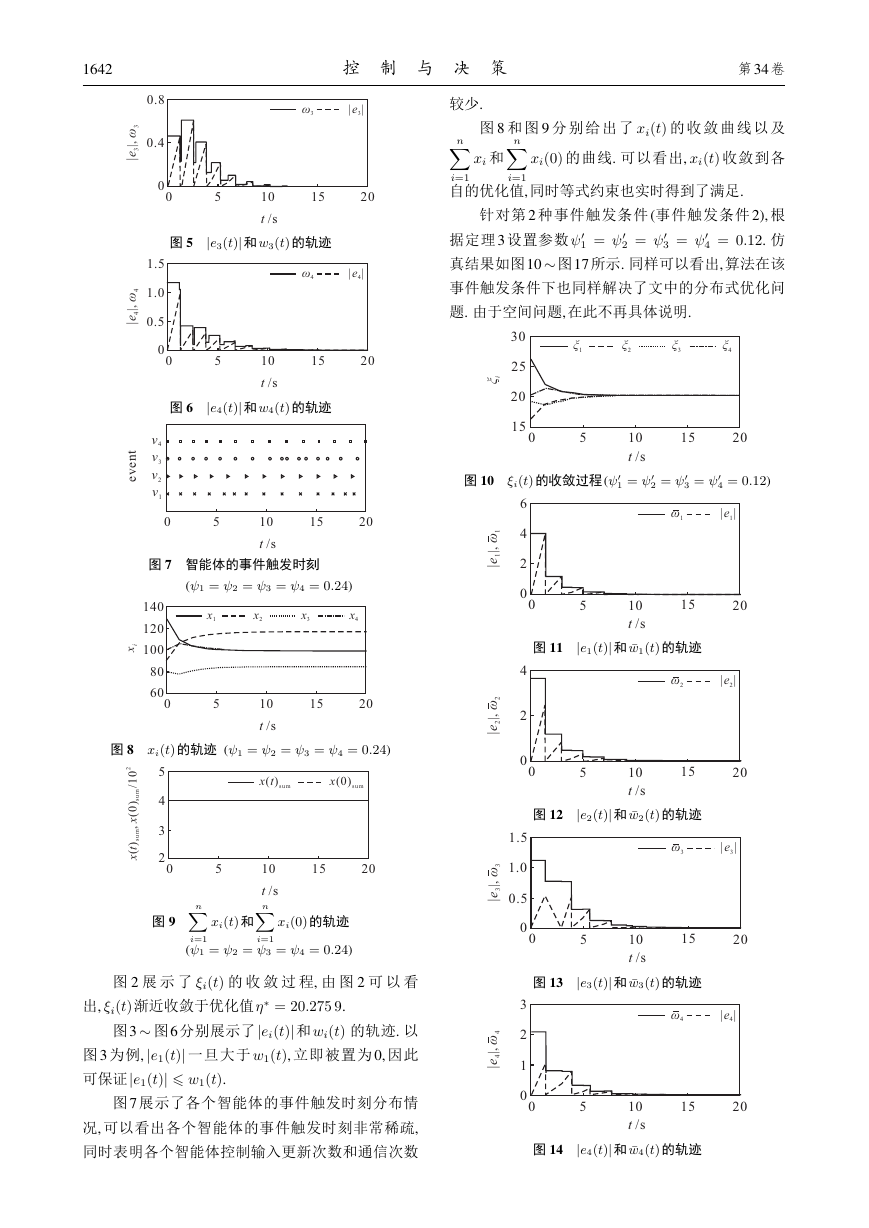
针对第 2 种事件触发条件 (事件触发条件 2), 根
′
据定理3 设置参数
4 = 0:12. 仿
真结果如图10 图17 所示. 同样可以看出, 算法在该
事件触发条件下也同样解决了文中的分布式优化问
题. 由于空间问题,在此不再具体说明.
′
2 =
′
3 =
图 10 i(t) 的收敛过程(
′
1 =
′
2 =
′
3 =
′
4 = 0:12)
图 11 je1(t)j 和 w1(t) 的轨迹
图 12 je2(t)j 和 w2(t) 的轨迹
图 13 je3(t)j 和 w3(t) 的轨迹
图 5 je3(t)j 和 w3(t) 的轨迹
图 6 je4(t)j 和 w4(t) 的轨迹
图 7 智能体的事件触发时刻
( 1 = 2 = 3 = 4 = 0:24)
图 8 xi(t) 的轨迹 ( 1 = 2 = 3 = 4 = 0:24)
n∑
图 9
n∑
xi(t) 和
xi(0) 的轨迹
i=1
i=1
( 1 = 2 = 3 = 4 = 0:24)
图 2 展 示 了 i(t) 的 收 敛 过 程, 由 图 2 可 以 看
出, i(t)渐近收敛于优化值
= 20:275 9.
图3 图6 分别展示了jei(t)j 和 wi(t) 的轨迹. 以
图 3 为例,je1(t)j 一旦大于 w1(t), 立即被置为 0, 因此
可保证je1(t)j ⩽ w1(t).
图7 展示了各个智能体的事件触发时刻分布情
况, 可以看出各个智能体的事件触发时刻非常稀疏,
同时表明各个智能体控制输入更新次数和通信次数
图 14 je4(t)j 和 w4(t) 的轨迹
05101520t/s0.80.40|eω33|,ω3|e3|05101520t/s1.50.50|eω44|,ω4|e4|1.005101520t/sv4eventv3v2v105101520t/s1401208060xix1x2x3x410005101520t/s542xtx()(0)sumsum,/102xt()sumx(0)sum305101520t/s30252015ξiξ1ξ2ξ3ξ405101520t/s620|eω11|,ω1|e1|405101520t/s420|eω22|,ω2|e2|05101520t/s1.50.50|eω33|,ω3|e3|1.005101520t/s320|eω44|,ω4|e4|1
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
