2010年云南昆明理工大学普通物理考研真题A卷.doc

发布时间：2022-09-17 发布人：admin 分类：说明书资料大小：0.08M 资料格式：doc 举报版权申诉

第1页 / 共3页

第2页 / 共3页

第3页 / 共3页

文本预览

2010 年云南昆明理工大学普通物理考研真题 A 卷一、名词解释（共 30 分。学术型学位及专业型学位研究生均做）： 1．简谐运动（5 分） 2. 转动惯量（5 分） 3. 熵、吉布斯自由能（10 分） 4. 干涉（5 分） 5. 保守力（5 分）二、计算题（共 120 分）（本大题分为两个部分，各部分总分均为 120 分：第一部分学术型学位研究生做，第二部分专业型学位研究生做。选做非本部分的题，均作 0 分处理。） ……………「「计算题第一部分：学术型学位研究生做」」…………… 1. 直线 1 与椭圆弧 2 分别表示两质点 A、B从同一地点出发，沿同一方向做直线运动的 v-t 图。已知 B的初速 v0=b m/s,它的速率由 v0 变为 0 所化的时间为 t1= 2b s，且椭圆与图中 v 轴、 t 轴相交处均为 90°，（1）试求 B在时刻 t 的加速度；（5 分）（2）设在 B停止时，A恰好追上 B，求 A的速度；（5 分）（3）在什么时候，A、B的速度相同？（5 分） 2. 一个人站在一竹筏的一端用力向垂直于筏身方向水平跳出去。筏由于受到反冲作用就要旋转起来。假定人的质量为 m = 60kg，筏的质量 M =500kg，人相对于岸的起跳速度为 3m ／s。求竹筏所获得的角速度。（假定竹筏的转动惯量近似地可以用细杆的公式来计算，水的摩擦可以忽略不计）。筏长 10 m。（15 分） 3. 一物体放在水平木板上，此板沿水平方向作简谐振动，频率为 2Hz，物体与板面间的静摩擦系数为 0.50。问: （1）要使物体在板上不致滑动，振幅的最大值为若干?（10 分）（2）若令此板改作竖直方向的简谐振动，振幅为 0.05m，要使物体一直保持与板接触的最大频率是多少?（10 分） 4. 一铜导线载有电流 I，I 均匀地分布在它的横截面上。已知导线横截面的半径为 R，铜内参加导电的自由电子密度为 n，电子电量为-e。求导线的中轴线与表面之间的电势差 U。（20 分） 5. 两个滑块的质量分别为 mA、mB，用弹性系数为 K 的轻弹簧将其相连并置于光滑的水平面上。将它们略微靠拢后同时松开，证明两滑块的相对运动为简谐运动并求出该简谐运动的角频率（假定弹簧不受力时的长度为 0l ）。（15 分） 6. 长为 L 的圆柱形电容器由半径为 a 的内芯导线及半径为 b 的外部导体薄壳组成，其间填

满了介电常数为ε的电介质。（1）当此电容器充电到带电量为 Q 时，求电场强度与径向位置的函数关系；（5 分）（2）求电容器的电容；（5 分）（3）把电容器与电势为 V 的电池连接，并将电介质从电容器中拉出一部分，当不计边缘效应时，如果维持电介质在此位置不动，要施加多大的力？此力沿什么方向？（10 分） 7. 如图所示，半径为 R1 的导体球面电荷为 q，在它外面同心地罩一个金属球壳，其内外壁的半径为 R2 与 R3，已知 R2=2R1，R3=3R1。令在距球心为 d=4R1 处放一电量为 Q 的点电荷，并将球壳接地。试求球壳带的总电量。（15 分） ……………「「计算题第二部分：专业型学位研究生做」」…………… 1. 压强为 1.0×105Pa，体积为 0.0082m3 的氮气，从初始温度 300K 加热到 400K，加热时(1) 体积不变，(2) 压强不变，问各需热量多少？哪一个过程所需热量大？（10 分）为什么？（5 分） 2. 声音在空气中的传播可以看作是一绝热过程。它的速度可按公式 v  p   计算（式中 γ为绝热指数，  ；p为空气的压强；ρ为空气的质量密度）。试证明声音在空气中 p C C V 的传播速度仅是温度的函数（假定空气可以视为理想气体）。（15 分） 3. 1mol 氢，在压强为 1.0×105Pa，温度为 200℃时，其体积为 0V ，今使它经以下两种过程达同一状态：（20 分） (1)先保持体积不变，加热使其温度升高到 800℃，然后令它作等温膨胀，体积变为原体积的 2 倍； (2)先使它作等温膨胀至原体积的 2 倍，然后保持体积不变，加热到 800℃。试分别计算以上两种过程中吸收的热量，气体对外作的功和内能的增量；并作 p~V图。 4. 在圆柱形区域内，沿轴向有一均匀磁场，如图所示，磁感应强度为 B，且 /dB dt 以恒定值增大。一个边长为 L 的正方形金属框置于该磁场中，框面垂直于轴线，轴线与框的一边 ad 相交

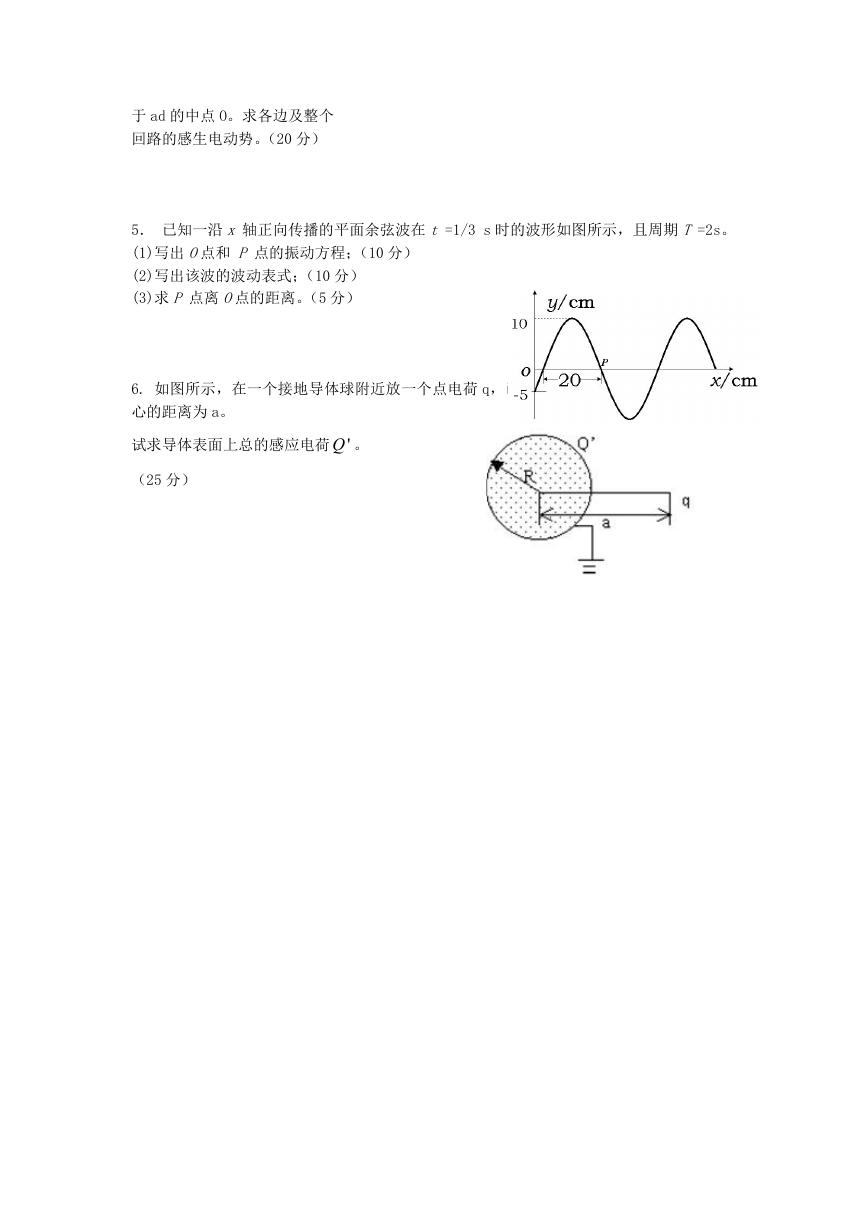
于 ad 的中点 O。求各边及整个回路的感生电动势。（20 分） 5．已知一沿 x 轴正向传播的平面余弦波在 t =1/3 s 时的波形如图所示，且周期 T =2s。 (1)写出 O点和 P 点的振动方程；（10 分） (2)写出该波的波动表式；（10 分） (3)求 P 点离 O点的距离。（5 分） 6. 如图所示，在一个接地导体球附近放一个点电荷 q，已知球的半径为 R，点电荷 q 与球心的距离为 a。试求导体表面上总的感应电荷 'Q 。（25 分）

分享到：

赞收藏

资料库

2010年云南昆明理工大学普通物理考研真题A卷.doc

相关推荐

考研

热门标签

最新资料