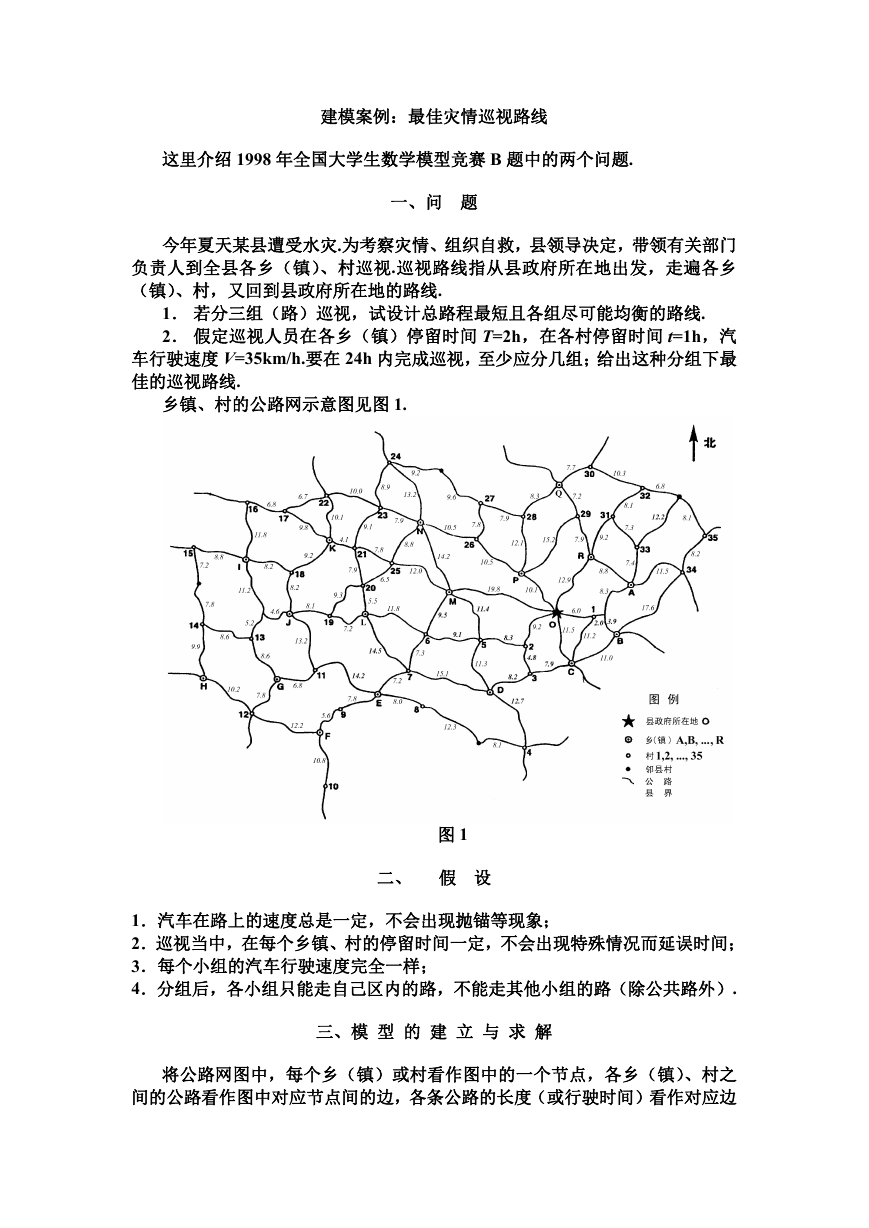
建模案例：最佳灾情巡视路线 这里介绍 1998 年全国大学生数学模型竞赛 B 题中的两个问题. 一、问 题 今年夏天某县遭受水灾.为考察灾情、组织自救，县领导决定，带领有关部门 负责人到全县各乡（镇）、村巡视.巡视路线指从县政府所在地出发，走遍各乡 （镇）、村，又回到县政府所在地的路线. 1． 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的路线. 2． 假定巡视人员在各乡（镇）停留时间 T=2h，在各村停留时间 t=1h，汽 车行驶速度 V=35km/h.要在 24h 内完成巡视，至少应分几组；给出这种分组下最 佳的巡视路线. 乡镇、村的公路网示意图见图 1. 图 1 二、 假 设 1．汽车在路上的速度总是一定，不会出现抛锚等现象； 2．巡视当中，在每个乡镇、村的停留时间一定，不会出现特殊情况而延误时间； 3．每个小组的汽车行驶速度完全一样； 4．分组后，各小组只能走自己区内的路，不能走其他小组的路（除公共路外）. 三、模 型 的 建 立 与 求 解 将公路网图中，每个乡（镇）或村看作图中的一个节点，各乡（镇）、村之 间的公路看作图中对应节点间的边，各条公路的长度（或行驶时间）看作对应边 

上的权，所给公路网就转化为加权网络图，问题就转化为在给定的加权网络图中 寻找从给定点 O 出发，行遍所有顶点至少一次再回到 O 点，使得总权（路程或 时间）最小，此即最佳推销员回路问题. 在加权图 G 中求最佳推销员回路问题是 NP—完全问题，我们采用一种近似 算法求出该问题的一个近似最优解，来代替最优解，算法如下：  ,  )  E  ( EVG ，   , yx 算法一 求加权图 G（V，E）的最佳推销员回路的近似算法： 1． 用 图论 软件 包求 出 G 中 任意 两个 顶点 间的 最短 路， 构造 出 完备 图 , x y mind ，   2． 输入图G 的一个初始 H 圈； 3． 用对角线完全算法产生一个初始 H 圈； 4． 随机搜索出G 中若干个 H 圈，例如 2000 个； 5． 对第 2、3、4 步所得的每个 H 圈，用二边逐次修正法进行优化，得到近 , x y ；     G 6． 在第 5 步求出的所有 H 圈中，找出权最小的一个，此即要找的最佳 H 似最佳 H 圈； 圈的近似解. 由于二边逐次修正法的结果与初始圈有关，故本算法第 2、3、4 步分别用三 种方法产生初始圈，以保证能得到较优的计算结果. 问题一 若分为 3 组巡视，设计总路程最短且各组尽可能均衡的巡视路线. 划分 1 , V ，将 G 分成 n 个生成子图  此问题是多个推销员的最佳推销员回路问题.即在加权图 G 中求顶点集 V 的 , , V V 2 n （1）顶点 （2） V i=1，2，3,…,n；  G V ，使得  G V G V 2 iVO  ,  i  ,..., ；    , 1 n  C j   ，其中 iC 为 iV 的导出子图   iVG 中的最佳推 n  1 i  m ax j i , GV   C  i m ax  i     C i （3） 销员回路，  iC 为 iC 的权，i，j=1，2，3,…,n；  C 取最小. （4）   n i i  1 定义 称  0   C j  m ax j i ,   C  i m ax  i     C i 为该分组的实际均衡度.为最大容 许均衡度. 显然 0  ， 0 越小，说明分组的均衡性越好.取定一个后， 0 与满 0  1 足条件（3）的分组是一个均衡分组.条件（4）表示总巡视路线最短. 此问题包含两方面：第一，对顶点分组；第二，在每组中求最佳推销员回路， 即为单个推销员的最佳推销员问题. 由于单个推销员的最佳推销员回路问题不存在多项式时间内的精确算法，故 多个推销员的问题也不存在多项式时间内的精确算法.而图中节点数较多，为 53 个，我们只能去寻求一种较合理的划分准则，对图１进行粗步划分后，求出各部 

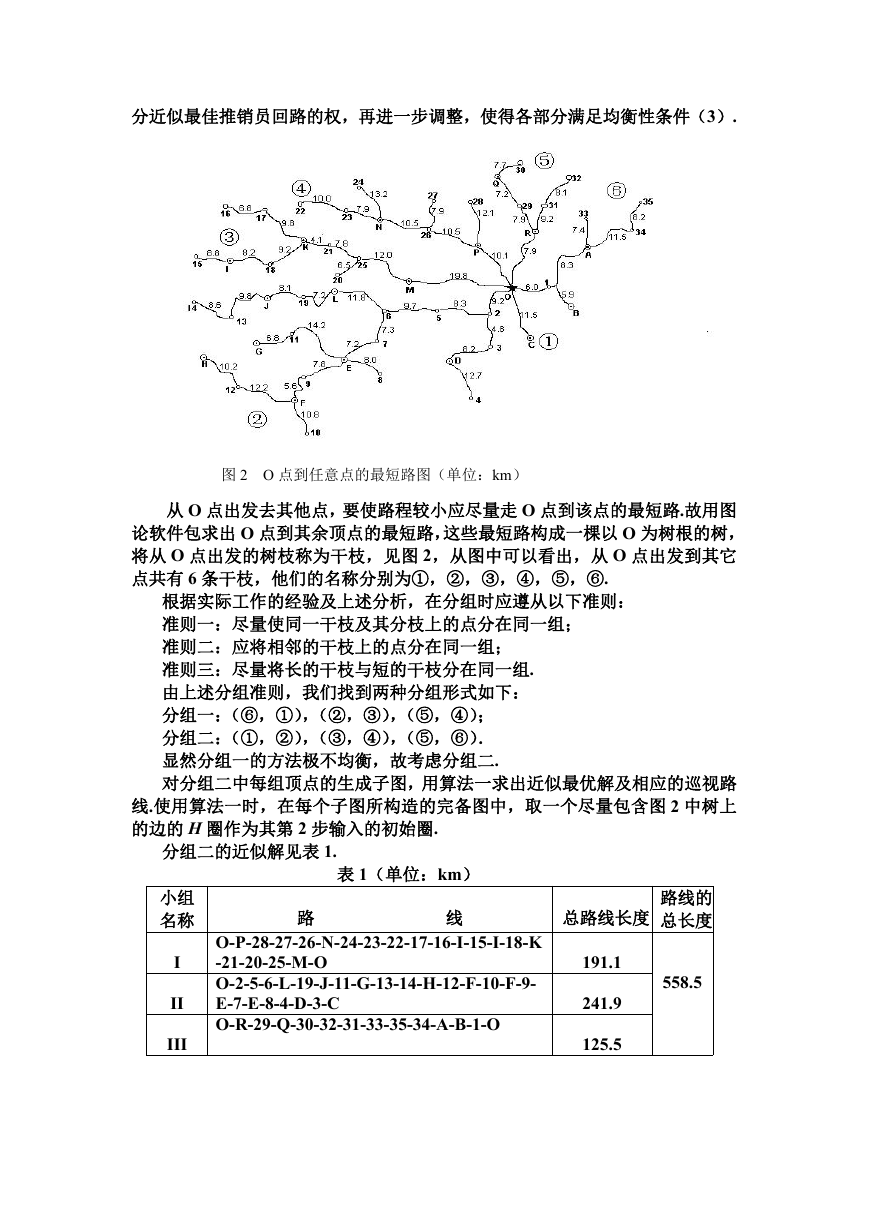
分近似最佳推销员回路的权，再进一步调整，使得各部分满足均衡性条件（3）. 图 2 O 点到任意点的最短路图（单位：km） 从 O 点出发去其他点，要使路程较小应尽量走 O 点到该点的最短路.故用图 论软件包求出 O 点到其余顶点的最短路，这些最短路构成一棵以 O 为树根的树， 将从 O 点出发的树枝称为干枝，见图 2，从图中可以看出，从 O 点出发到其它 点共有 6 条干枝，他们的名称分别为①，②，③，④，⑤，⑥. 根据实际工作的经验及上述分析，在分组时应遵从以下准则： 准则一：尽量使同一干枝及其分枝上的点分在同一组； 准则二：应将相邻的干枝上的点分在同一组； 准则三：尽量将长的干枝与短的干枝分在同一组. 由上述分组准则，我们找到两种分组形式如下： 分组一：（⑥，①），（②，③），（⑤，④）； 分组二：（①，②），（③，④），（⑤，⑥）． 显然分组一的方法极不均衡，故考虑分组二. 对分组二中每组顶点的生成子图，用算法一求出近似最优解及相应的巡视路 线.使用算法一时，在每个子图所构造的完备图中，取一个尽量包含图 2 中树上 的边的 H 圈作为其第 2 步输入的初始圈. 分组二的近似解见表 1. 表 1（单位：km） 小组 名称 I II III 路 线 总路线长度 O-P-28-27-26-N-24-23-22-17-16-I-15-I-18-K -21-20-25-M-O O-2-5-6-L-19-J-11-G-13-14-H-12-F-10-F-9- E-7-E-8-4-D-3-C O-R-29-Q-30-32-31-33-35-34-A-B-1-O 191.1 241.9 125.5 路线的 总长度 558.5 

因为该分组的均衡度 0 =    C 1 max 1,2,3 i      C  C  i  2  241.9 125.5  241.9  54.2% 所以此分法的均衡性很差. 为改善均衡性，将第Ⅱ组中的顶点 C，2，3，D，4 分给第Ⅲ组（顶点 2 为 这两组的公共点），重新分组后的近似最优解见表 2. 表 2（单位：km） 编号 路 线 I II III O—P—28—27—26—N—24—23—22—17 —16—I—15—I—18—K—21—20—25—M —O O—2—5—6—7—E—8—E—9—F—10—F —12—H—14—13—G—11—J—19—L—6 —5—2—O O—R—29—Q—30—32—31—33—35—34 —A—1—B—C—3—D—4—D—3—2—O 路线总 长度 599.8 路线 长度 191.1 216.4 192.3 因该分组的均衡度 0    C    3  max C  i 1,2,3 i  所以这种分法的均衡性较好.  C 1   216.4 191.1  216.4  11.69% 问题二 当巡视人员在各乡（镇）、村的停留时间一定，汽车的行驶速度一 定，要在 24h 内完成巡视，至少要分几组及最佳的巡视路线. 由于 T=2h，t=1h，V=35km/h，需访问的乡镇共有 17 个，村共有 35 个.计算 出在乡（镇）及村的总停留时间为 172h+35h=69h，要在 24h 内完成巡回，若 不考虑行走时间，有: (i 为分的组数).得 i 最小为 4，故至少要分 4 组. 24 69  i 由于该网络的乡（镇）、村分布较为均匀，故有可能找出停留时间尽量均衡 的分组，当分 4 组时各组停留时间大约为 69 h 17.25 h，则每组分配在路途上的 时间大约为 24h-17.25h=6.75h.而前面讨论过，分三组时有个总路程 599.8km 的 巡视路线，分 4 组时的总路程不会比 599.8km 大太多，不妨以 599.8km 来计算. 路上时间约为 599.8 h 17 17 h=4.25h 4 〈6.75h，故分成 4 组是可能办到的. h，若平均分配给 4 个组，每个组约需 35 4   现在尝试将顶点分为 4 组.分组的原则：除遵从前面准则一、二、三外，还应 遵从以下准则： 准则四：尽量使各组的停留时间相等. 用上述原则在图 2 上将图分为 4 组，同时计算各组的停留时间,然后用算法一 算出各组的近似最佳推销员巡回，得出路线长度及行走时间，从而得出完成巡视 的近似最佳时间.用算法一计算时，初始圈的输入与分 3 组时同样处理. 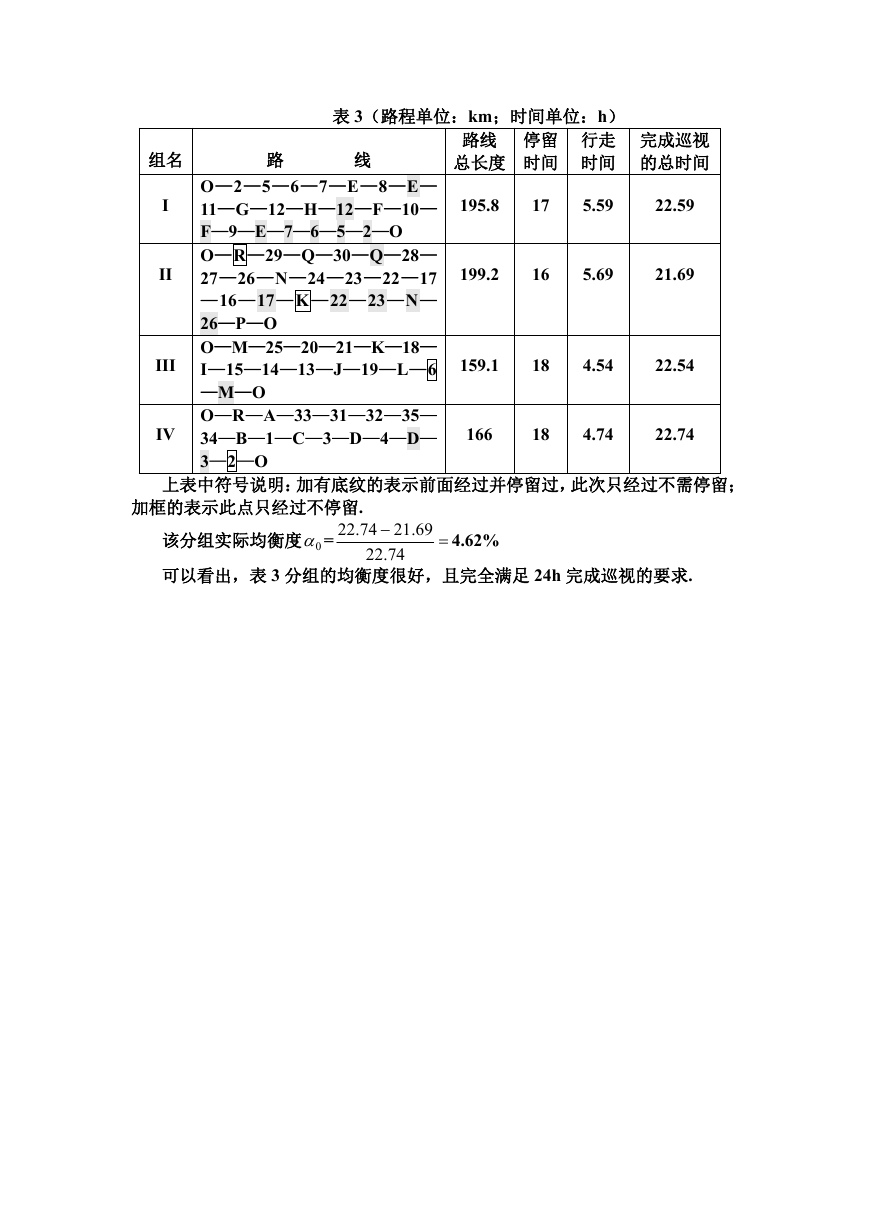这 4 组的近似最优解见表 3. 

组名 路 表 3（路程单位：km；时间单位：h） 行走 时间 停留 时间 总长度 路线 线 完成巡视 的总时间 I II III IV O—2—5—6—7—E—8—E— 11—G—12—H—12—F—10— F—9—E—7—6—5—2—O O—R—29—Q—30—Q—28— 27—26—N—24—23—22—17 —16—17—K —22—23—N— 26—P—O O—M—25—20—21—K—18— I—15—14—13—J—19—L—6 —M—O O—R—A—33—31—32—35— 34—B—1—C—3—D—4—D— 3—2—O 195.8 199.2 159.1 166 17 16 18 18 5.59 22.59 5.69 21.69 4.54 22.54 4.74 22.74 上表中符号说明：加有底纹的表示前面经过并停留过，此次只经过不需停留； 加框的表示此点只经过不停留. 74.22  该分组实际均衡度 0 = 可以看出，表 3 分组的均衡度很好，且完全满足 24h 完成巡视的要求. 4.62% 74.22  69.21